Credible Interval Prediction of a Nonstationary Poisson Distribution
based on Bayes Decision Theory
Daiki Koizumi
a
Otaru University of Commerce, 3–5–21, Midori, Otaru-city, Hokkaido, 045–8501, Japan
Keywords:
Bayes Decision Theory, Credible Interval, Nonstationary Poisson Distribution.
Abstract:
A credible interval prediction problem of a nonstationary Poisson distribution in terms of Bayes decision the-
ory is considered. This is the two-dimensional optimization problem of the Bayes risk function with respect
to two variables: upper and lower limits of credible interval prediction. We prove that these limits can be
uniquely obtained as the upper or lower percentile points of the predictive distribution under a certain loss
function. By applying this approach, the Bayes optimal prediction algorithm for the credible interval is pro-
posed. Using real web traffic data, the performance of the proposed algorithm is evaluated by comparison with
the stationary Poisson distribution.
1 INTRODUCTION
The credible interval (or credibility interval) (Berger,
1985; Press, 2003) is a Bayesian interval estimation
method defined by a set function with a simpler defi-
nition compared to the confidence interval. Since it is
a more general estimation method than the Bayesian
point estimation, a specific approach (Winkler, 1972)
in terms of Bayes decision theory (Weiss and Black-
well, 1961; Berger, 1985) is proposed. In this ap-
proach, the Bayesian credible interval parameter es-
timation method is considered on the assumption of
a certain loss function. Specifically, assuming power
loss functions, the necessary and sufficient conditions
to obtain a unique credible interval solution as the
minimizer of the posterior expected loss is discussed.
On the other hand, the Poisson distribution is
a well-known probability mass function in various
fields. Especially if counting data with a probabil-
ity model is considered, the Poisson distribution is
one important choice. In basic modeling, the station-
ary Poisson distribution is often defined, which means
that its parameter is time independent. However, for
a certain types of counting data such as web traffic,
the stationary Poisson distribution can be insufficient.
Accordingly, the author previously proposed a new
class of nonstationary Poisson distribution (Koizumi
et al., 2009). In this nonstationary Poisson distribu-
tion, its parameter was time dependent and changing
a
https://orcid.org/0000-0002-5302-5346
with random walking. This nonstationary class was
defined as a transforming function of a random vari-
able with a single hyper parameter. Then, assuming
the squared loss function to measure the predictive
error, the Bayes optimal predictive point estimator in
terms of Bayes decision theory was obtained. This es-
timator can be calculated with simple arithmetic op-
erations under both a certain assumption for the prior
distribution of the parameter and the known value of
the nonstationary single hyper parameter. Further-
more, this estimator enables the online prediction al-
gorithm and its predictive error (mean squared error,
MSE) from real web traffic data was shown to be
smaller than that of the stationary Poisson distribu-
tion.
In fact, the above Bayes optimal point predictive
estimator was defined as the expectation of the pre-
dictive distribution. If the squared loss function is
defined, then this is natural in terms of Bayes deci-
sion theory. In a statistical sense, the expectation can
be interpreted as the “central value” of the probabil-
ity distribution. However, in some fields like web
traffic analysis, system operators may be concerned
with not the central value but the “upper value” of the
request arrival. In order to discuss those upper val-
ues of the distribution, the credible interval with a set
function can be a useful definition in the context of
Bayesian statistics. Furthermore, the credible interval
estimation is the generalization of point estimation.
These points are expected to enable the credible in-
terval prediction algorithm to be proposed using the
Koizumi, D.
Credible Interval Prediction of a Nonstationary Poisson Distribution based on Bayes Decision Theory.
DOI: 10.5220/0009182209951002
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 995-1002
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
995

author’s nonstationary Poisson distribution. This pa-
per discusses these points.
The remainder of this paper is organized as fol-
lows. Section 2 provides the basic definitions of the
nonstationary Poisson distribution and two theorems
in terms of Bayesian statistics. Section 2 also de-
scribes the conventional results for the credible inter-
val parameter estimation problem in terms of Bayes
decision theory. Section 3 formulates the credible in-
terval prediction problem, derives a theorem in terms
of Bayes decision theory, and proposes the prediction
algorithm. Section 4 gives some numerical examples
with real web traffic data. Section 5 discusses the re-
sults. Section 6 draws some conclusions of this paper.
2 PRELIMINARIES
2.1 Web Traffic Modeling with
Nonstationary Poisson Distribution
Let t = 1,2,... be a discrete time index and X
t
= x
t
≥
0 be a discrete random variable at t. Assume that
web Traffic at time is X
t
and X
t
∼ Poisson(θ
t
), where
θ
t
> 0, is a nonstationary parameter. Thus, the prob-
ability density function of the nonstationary Poisson
distribution p

x
t


θ
t

is defined as follows:
Definition 2.1. Nonstationary Poisson Distribution
p

x
t


θ
t

=
exp(−θ
t
)
x
t
!
(θ
t
)
x
t
, (1)
where θ
t
> 0. 2
A nonstationary class of parameters θ
t
is defined
as random walking:
Definition 2.2. Nonstationary Class of Parameter
θ
t+1
=
u
t
k
θ
t
, (2)
where 0 < k ≤ 1, 0 < u
t
< 1. 2
In Eq. (2), a real number 0 < k ≤ 1 is a known con-
stant, U
t
= u
t
is a continuous random variable, where
0 < u
t
< 1. The probability distribution of u
t
is de-
fined in Definition 2.5.
The parameter Θ
t
= θ
t
is a continuous random
variable from a Bayesian viewpoint. The prior Θ
1
∼
Gamma(α
1
,β
1
), where θ
1
> 0, α
1
> 0, and β
1
> 0.
This prior distribution is defined as follows:
Definition 2.3. Prior Gamma Distribution for θ
1
p

θ
1


α
1
,β
1

=
(β
1
)
α
1
Γ(α
1
)
(θ
1
)
α
1
−1
exp(−β
1
θ
1
),(3)
where α
1
> 0,β
1
> 0 and Γ(·) is the gamma function
defined in Definition 2.4. 2
Definition 2.4. Gamma Function
Γ(a) =
Z
∞
0
b
a−1
exp(−b)db , (4)
where b ≥ 0. 2
∀t, U
t
∼ Beta[kα
t
,(1 − k)α
t
], where 0 < u
t
<
1, 0 < k ≤ 1, and α
t
> 0. Its probability density func-
tion is defined as follows:
Definition 2.5. Beta Distribution for u
t
p

u
t


kα
t
,(1 − k)α
t

=
Γ(α
t
)
Γ(kα
t
)Γ[(1 − k)α
t
]
(u
t
)
kα
t
−1
(1 − u
t
)
(1−k)α
t
−1
.
(5)
2
Random variables θ
t
,u
t
are conditional independent
under α
t
. This is defined as follows:
Definition 2.6. Conditional Independence for θ
t
,u
t
under α
t
p

θ
t
,u
t


α
t

= p

θ
t


α
t

p

u
t


α
t

. (6)
2
Let x
x
x
t−1
= (x
1
,x
2
,.. .,x
t−1
) be the observed
data sequence. Then, the posterior distribution
p

θ
t


α
t
,β
t
,x
x
x
t−1

can be obtained with the follow-
ing closed form.
Theorem 2.1. Posterior Distribution of θ
t
∀t ≥ 2, Θ
t


x
x
x
t−1
∼ Gamma (α
t
,β
t
). This means
that the posterior distribution p

θ
t


α
t
,β
t
,x
x
x
t−1

sat-
isfies the following:
p

θ
t


α
t
, β
t
, x
x
x
t−1

=
(β
t
)
α
t
Γ(α
t
)
(θ
t
)
α
t
−1
exp(−β
t
θ
t
),
(7)
where its parameters α
t
,β
t
are given as,







α
t
= k
t−1
α
1
+
t−1
∑
i=1
k
t−i
x
i
;
β
t
= k
t−1
β
1
+
t−1
∑
i=1
k
i−1
.
(8)
2
Proof of Theorem 2.1.
See APPENDIX A. 2
Theorem 2.2. Predictive Distribution of x
t+1
p

x
t+1


x
x
x
t

=
Γ(α
t+1
+ x
t+1
)
x
t+1
!Γ(α
t+1
)

β
t+1
β
t+1
+ 1

α
t+1

1
β
t+1
+ 1

x
t+1
,
(9)
where α
t+1
,β
t+1
are given as Eqs. (9).
2
Proof of Theorem 2.2.
See APPENDIX B. 2
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
996

2.2 Credible Interval Parameter
Estimation based on Bayes Decision
Theory
Interval estimation is defined by a set function in con-
trast to point estimation defined by single value. This
interval is particularly called as credible interval in
terms of Bayesian method. Let C = [a,b],a ≤ b be a
credible interval. Then, 100 (1 − λ) % credible inter-
val for θ
t
can be defined as follows:
Definition 2.7. Credible Interval Parameter Estima-
tion for θ
t
(Berger, 1985)
1 − λ ≤ p

C


x
x
x
t

=
Z
b
a
p

θ
t


x
x
x
t

dθ
t
, (10)
where 0 ≤ λ < 1. 2
Definition 2.8. Loss Function for Credible Interval
Estimation (Winkler, 1972)
L
1
(a,b,θ
t
)
=





L
u
(θ
t
− b) + r (b − a), if b ≤ θ
t
;
r (b − a) , if a ≤ θ
t
≤ b;
L
o
(a − θ
t
) + r (b − a), if θ
t
≤ a,
(11)
where r > 0 and, L
u
,L
o
are monotone nondecreasing
function with L
o
(x) = L
u
(x) = 0 for all x ≤ 0. 2
Definition 2.9. Expected Loss (Winkler, 1972)
EL (a, b)
=
Z
+∞
0
L
1
(a,b,θ
t
) p

θ
t


x
x
x
t

dθ
t
=
Z
a
0
L
o
(a − θ
t
) p

θ
t


x
x
x
t

dθ
t
+
Z
+∞
b
L
u
(θ
t
− b) p

θ
t


x
x
x
t

dθ
t
+ r (a − b).(12)
2
With the above definitions, the Bayes optimal
credible interval [ ˆa,
ˆ
b] for θ
t
is obtained as follows:
ˆa = argmin
a
EL (a, b) , (13)
ˆ
b = argmin
b
EL (a, b) . (14)
Thus the credible interval with decision theoretic
approach is obtained as the two dimensional opti-
mization problem. However, this problem does not
always guarantee the unique optimal solution. To do
so, more restrictive conditions are needed. The fol-
lowing two propositions solve this problem.
Proposition 2.1. (Winkler, 1972)
If L
o
,L
u
are convex and not everywhere constant,
EL (a, b) is finite for all (a, b), then EL (a,b) has a
minimum value and the set of optimal intervals (a, b)
is a bounded convex set. If, in addition, either L
o
or
L
u
is strictly convex, the optimal interval is unique. 2
Proposition 2.2. (Winkler, 1972)
If L
o
,L
u
are twice differentiable on [0, ∞) and the
optimal interval has non zero length, then necessary
first- and second-order conditions for (a, b) to be op-
timal are,
Z
a
0
L
0
o
(a − θ
t
) p

θ
t


x
x
x
t

dθ
t
=
Z
+∞
b
L
0
u
(θ − b) p

θ
t


x
x
x
t

dθ
t
= r , (15)
Z
a
0
L
00
o
(a − θ
t
) p

θ
t


x
x
x
t

dθ
t
+L
0
o
(0) p

a


x
x
x
t

≥ 0, (16)
Z
+∞
b
L
00
u
(θ
t
− b) p

θ
t


x
x
x
t

dθ
t
+L
0
u
(0) p

b


x
x
x
t

≥ 0. (17)
2
Lemma 2.1. (Winkler, 1972)
Let denote the loss function as the following power
function,
L
2
(a,b,θ
t
)
=





c
1
(θ
t
− b)
q
+ c
3
(b − a) , if b ≤ θ
t
;
c
3
(b − a) , if a ≤ θ
t
≤ b;
c
2
(a − θ
t
)
r
+ c
3
(b − a) , if θ
t
≤ a,
(18)
where c
1
,c
2
,c
3
,q,r > 0,
then, the necessary first-order condition corre-
sponding Eq. (15) is,
qc
1
Z
+∞
b
(θ
t
− b)
q−1
p

θ
t


x
x
x
t

dθ
= rc
2
Z
a
0
(a − θ
t
)
r−1
p

θ
t


x
x
x
t

dθ
= c
3
. (19)
2
Lemma 2.2. (Winkler, 1972)
If q = r = 1 in Eq. (18), then the first-order nec-
essary condition is,
Z
a
0
p

θ
t


x
x
x
t

dθ
t
=
c
3
c
2
, (20)
Z
+∞
b
p

θ
t


x
x
x
t

dθ
t
=
c
3
c
1
. (21)
Furthermore, if (c
3
/c
1
) + (c
3
/c
2
) < 1, then the
Bayes optimal solution

ˆa,
ˆ
b

, ˆa <
ˆ
b in Eqs. (13) and
(14) exists. 2
Lemma 2.2 states the credible interval parame-
ter estimation for θ
t
based on Bayes decision theory.
However, this is not a prediction problem for x
t+1
but
the parameter estimation problem. The credible inter-
val prediction problem based on Bayes decision the-
ory is formulated in the next section.
Credible Interval Prediction of a Nonstationary Poisson Distribution based on Bayes Decision Theory
997

3 CREDIBLE INTERVAL
PREDICTION BASED ON
BAYES DECISION THEORY
This section formulates the credible interval predic-
tion problem based on Bayes decision theory (Weiss
and Blackwell, 1961; Berger, 1985). Defining the
loss, the risk, and the Bayes risk functions, the Bayes
optimal credible interval prediction

ˆa
∗
,
ˆ
b
∗

for x
t+1
is
obtained as the minimizer of the Bayes risk function
BR(a,b).
Definition 3.1. Loss Function for Credible Interval
Prediction
L
3
(a,b,x
t+1
)
=





c
1
(x
t+1
− b) + c
3
(b − a) , if b ≤ x
t+1
;
c
3
(b − a) , if a ≤ x
t+1
≤ b;
c
2
(a − x
t+1
) + c
3
(b − a) , if x
t+1
≤ a,
(22)
where
c
3
c
1
+
c
3
c
2
< 1. 2
Definition 3.2. Risk Function
R(a,b, θ
t+1
)
=
+∞
∑
x
t+1
=0
L
3
(a,b,x
t+1
) p

x
t+1


θ
t+1

. (23)
2
Definition 3.3. Bayes Risk Function
BR(a,b)
=
Z
+∞
0
R(a,b, θ
t+1
) p

θ
t+1


x
x
x
t

dθ
t+1
.(24)
2
Definition 3.4. Bayes Optimal Credible Interval Pre-
diction
ˆa
∗
= arg min
a
BR(a,b) , (25)
ˆ
b
∗
= arg min
b
BR(a,b) . (26)
2
Theorem 3.1. Bayes Optimality of Credible Interval
Prediction
If the loss function in Eq. (22) is defined in the
credible interval prediction problem, then the Bayes
optimal solution

ˆa
∗
,
ˆ
b
∗

, ˆa
∗
<
ˆ
b
∗
in Eqs. (25) and
(26) uniquely exists where ˆa
∗
,
ˆ
b
∗
satisfies,
Z
ˆa
∗
0
p

x
t+1


x
x
x
t

dx
t+1
=
c
3
c
2
, (27)
Z
+∞
ˆ
b
∗
p

x
t+1


x
x
x
t

dx
t+1
=
c
3
c
1
. (28)
2
Proof of Theorem 3.1.
Same proof as Lemma 2.2 (Winkler, 1972). In
Lemma 2.2, the objective function is the posterior
distribution of parameter p

θ
t


x
x
x
t

since the credible
interval parameter estimation problem is considered.
Only difference is that the objective function in The-
orem 3.1 is the predictive distribution p

x
t+1


x
x
x
t

for
credible interval prediction problem. 2
With both Definition 2.7 and Theorem 3.1, the di-
rect relationship between 100 (1 − λ) % credible inter-
val for x
t+1
in Eq. (10) and loss function in Eq. (22)
is obtained. Table 1 shows some parameter examples
of λ,c
1
,c
2
, and c
3
.
Table 1: Parameter Examples for Credible Intervals and
Loss Functions.
λ c
1
c
2
c
3
0.01 200 200 1
0.05 40 40 1
0.10 20 20 1
Based on the Theorem 3.1, the following Bayes op-
timal credible interval prediction algorithm is pro-
posed.
Algorithm 3.1. Proposed Algorithm
1. Define the parameters c
1
,c
2
, and c
3
for loss func-
tion in Eq.(22).
2. Estimate hyper parameter k in Eq. (2) from train-
ing data.
3. Set t = 1 and define the hyper parameters α
1
,β
1
for the initial prior p

θ
1


α
1
,β
1

in Eq. (3).
4. Update the posterior parameter distribution
p

θ
t


α
t
,β
t
,x
x
x
t

under both prior p

θ
t


α
t
,β
t

and observed test data x
x
x
t
in Eqs. (7) and (9).
5. Calculate the predictive distribution p

x
t+1


x
x
x
t

in Eq. (9).
6. Obtain the Bayes optimal credible interval

ˆa
∗
,
ˆ
b
∗

from Eqs. (27) and (28).
7. If t < t
max
, then set (t + 1) ← t, the prior
p(θ
t+1
) ← p

θ
t


α
t
,β
t
,x
x
x
t

, and back to 4.
8. If t = t
max
, then terminate the algorithm.
2
4 NUMERICAL EXAMPLES
This section shows numerical examples to evaluate
the performance of Algorithm 3.1. Subsection 4.1
explains both training and test data specifications.
Training data was used to estimate hyper parameter
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
998

k in Eq. (2). For estimation of
ˆ
k, the empirical Bayes
approach with the approximate maximum likelihood
estimation is considered. Its detail is explained in
subsection 4.2. The test was used to the credible in-
terval estimation. Defined parameters and evaluation
basis is described in subsection 4.3. Finally, results
are shown in subsection 4.4.
4.1 Web Traffic Data Specifications
Table 2 and 3 show the training and test data spec-
ifications. Both web traffic data were obtained by
recording the http request arrival time stamps every
3 minutes at the web server in the late Mar. 2005.
Table 2: Training Data Specifications.
Items Values
Date Mar. 25, 2005
Total Request Arrivals 11,527
Time Interval Every 3 minutes
Total Time Intervals t
max
= 305
Table 3: Test Data Specifications.
Items Values
Date Mar. 26, 2005
Total Request Arrivals 6,382
Time Interval Every 3 minutes
Total Time Intervals t
max
= 291
4.2 Hyper Parameter Estimation with
Empirical Bayes Method
Since a hyper parameter 0 < k ≤ 1 in Eq. (2) is as-
sumed to be known, it must be estimated for real
data analysis. In this paper, the following maximum
likelihood estimation with numerical approximation
in terms of empirical Bayes method is considered to
obtain
ˆ
k.
ˆ
k = argmax
k
L (k) , (29)
L (k)
= p

x
1


θ
1

t
∏
i=2
p

x
i


x
x
x
i−1
,k

(30)
= p

x
1


θ
1

·
t
∏
i=2

Z
+∞
0
p

x
i


x
x
x
i−1
,θi,k

p

θ
i


x
x
x
i−1

dθ
i

(31)
= p

x
1


θ
1

·
t
∏
i=2


(β
i
)
α
i
Γ(α
i
+ x
i
)
(β
i
+ 1)
α
i
+x
i
Γ(α
i
)x
i
!





α
i
= k
i−1
α
1
+
∑
i−1
j=1
k
i− j
x
j
β
i
= k
i−1
β
1
+
∑
i−1
j=1
k
j−1


.
(32)
In this data analysis, t = 305 from Table 2 was used
in the L(k) since the training data was applied to esti-
mate k. The numerically estimated value
ˆ
k was shown
in Table 6 of subsection 4.4.
4.3 Evaluations of Credible Interval
Prediction
For evaluations of credible interval prediction, the
proposed nonstationary and the conventional station-
ary Poisson distributions were considered. The Bayes
optimal credible interval predictions were derived for
both distributions.
Table 4 shows the initial prior distributions of
p

θ
1


α
1
,β
1

in Eq. (3). This initial condition
corresponds to the following non-informative prior
(Berger, 1985; Bernardo and Smith, 2000),
p(θ
1
) =
1
θ
1
. (33)
The following posterior calculation shows that the ini-
tial prior in Eq. (33) corresponds to α
1
,β
1
in Table 4.
By the Bayes theorem, the posterior p

θ
1


x
1

be-
comes,
p

θ
1


x
1

=
p

x
1


θ
1

p(θ
1
)
R
∞
0
p

x
1


θ
1

p(θ
1
)
(34)
=
exp(−θ
1
)(θ
1
)
x
1
−1
Γ(x
1
)
. (35)
Thus Eq. (35) shows that,
θ
1
|x
1
∼ Gamma(α
1
= x
1
,β
1
= 1).
Table 4: Defined Hyper Parameters for Prior distribution
p(θ
1
).
α
1
β
1
x
1
1
For the loss function in Eq. (22), Table 4 shows the
defined parameters c
1
,c
2
, and c
3
. For the proposed
prediction of

ˆa
∗
,
ˆ
b
∗

, 95% credible interval is con-
sidered. This means that ˆa
∗
and
ˆ
b
∗
correspond to the
lower 2.5 percentile and the upper 2.5 percentile (or
lower 97.5 percentile) points of the predictive distri-
bution p

x
t+1


x
x
x
t

, respectively.
Credible Interval Prediction of a Nonstationary Poisson Distribution based on Bayes Decision Theory
999

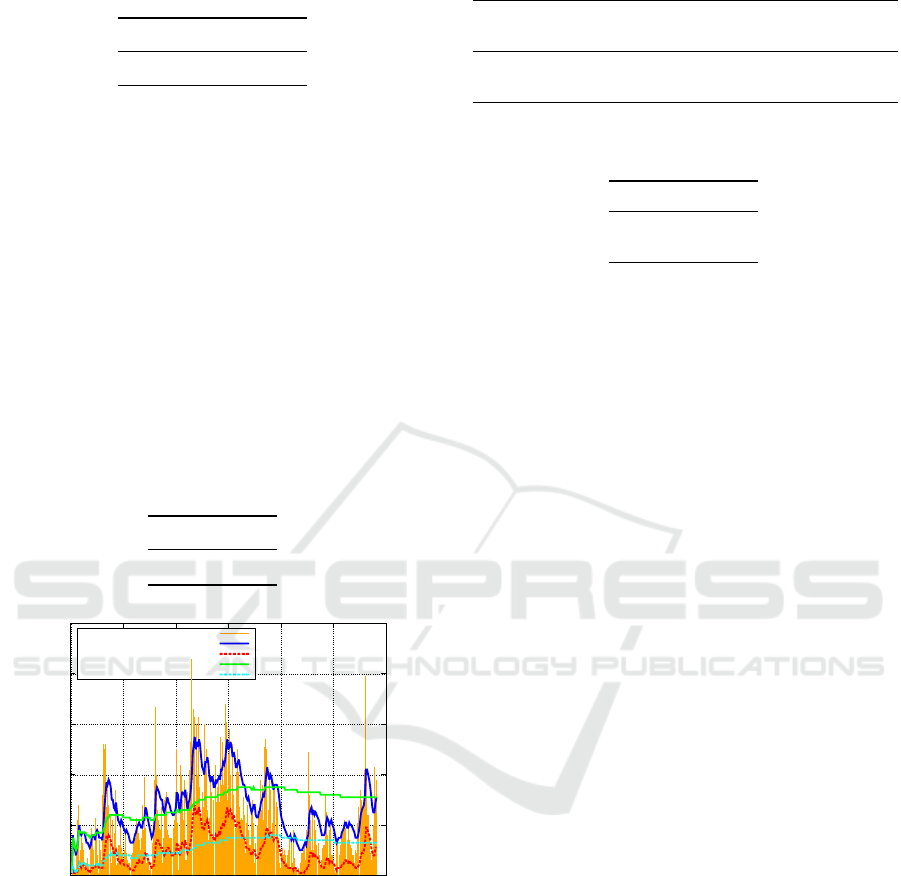
Table 5: Defined Parameters for Credible Intervals and Loss
Functions.
λ c
1
c
2
c
3
0.05 40 40 1
4.4 Results
Table 6 shows the estimated hyper parameter
ˆ
k from
training data. Based on this
ˆ
k, the proposed algorithm
3.1 is applied to obtain the Bayes optimal credible in-
terval prediction. Figure 1 shows its result. In Fig-
ure 1, the horizontal and vertical axes are the index of
time interval 1 ≤ t ≤ 291 and the number of request
arrival, respectively. Furthermore, the orange bar is
real request arrival x
t
, the blue solid line is the pro-
posed upper value of the credible interval prediction
ˆ
b
∗
, the red dotted line is the proposed lower value of
ˆa
∗
. The green solid and cyan dotted lines mean the
upper and lower limits of the credible interval predic-
tions from stationary Poisson distribution.
Table 6: Hyper Parameter Estimation from Training Data.
Item Value
ˆ
k 0.805
0
20
40
60
80
100
0 50 100 150 200 250 300
Numbers of Request Arrivals
t
Observed Values
Proposed (Upper2.5%)
Proposed (Lower2.5%)
Stationary (Upper2.5%)
Stationary(Lower2.5%)
Figure 1: Credible Interval Prediction for Test Data.
Table 7 shows the number of time intervals satisfying
ˆ
b
∗
≥ x
t
between the proposed nonstationary and con-
ventional stationary Poisson distributions. Moreover,
Table 8 shows the MSE between both models.
5 DISCUSSIONS
A hyper parameter k in the proposed nonstationary
class in Eq. (2) and (5) generalizes a stationary Pois-
son distribution to one with a nonstationary parame-
Table 7: Number of Time Intervals with
ˆ
b
∗
≥ x
t
.
Time Intervals Total Coverage
Items with
ˆ
b
∗
≥ x
t
Time Intervals Rate
Stationary 212 291 72.9%
Proposed 208 291 71.5%
Table 8: Mean Squared Error between Upper 2.5 Percentile
ˆ
b
∗
and x
t
for the Proposed and Stationary Models.
Items MSE
Stationary 293.8
Proposed 185.2
ter. If k = 1 in Eq. (2), θ
t+1
= u
t
θ
t
holds. In this case,
U
t
∼ Beta[α
t
,0] in Eq. (5). Since the second shape
parameter in the Beta distribution becomes zero, the
variance of u
t
also becomes zero. This implies that
the parameter θ
t
in the Poisson distribution of x
t
is
stationary. However, if 0 < k < 1 in Eq. (2), the pa-
rameter θ
t
in the Poisson distribution is nonstationary.
In Eq. (9), β
t
is expressed by the term
∑
t−1
i=1
k
i
(x
i
)
m
. This form is called the exponentially
weighted moving average (EWMA) (Smith, 1979,
p. 382),(Harvey, 1989, p. 350). The form is also ob-
served in several versions of Simple Power Steady
Model (Smith, 1979).
Theorem 3.1 implies that if the loss function in Eq.
(22) is defined, then the unique Bayes optimal cred-
ible interval prediction

ˆa
∗
,
ˆ
b
∗

is obtained. In this
case,
ˆ
b
∗
is the upper 100 (c
3
/c
1
) percentile point of
the predictive distribution p

x
t+1


x
x
x
t

. The ˆa
∗
is the
lower 100(c
3
/c
2
) percentile point of the p

x
t+1


x
x
x
t

likewise.
According to Table 6, the hyper parameter
ˆ
k =
0.805 which is smaller than k = 1 is obtained. This
implies that the training web traffic data can be esti-
mated as the nonstationary Poisson distribution. Ac-
tually in Figure 1, the proposed prediction lines seem
to flexibly follow the real traffic data well comparing
to the stationary prediction lines.
Table 8 also shows that MSE of the proposed
model is approximately 40% smaller than that of the
stationary model. If λ = 0.01, c
1
= c
2
= 200, and
c
3
= 1 from Table 1 are assumed to consider the upper
0.5% percentile
ˆ
b
∗
, then this MSE is expected to be
more smaller than that of the stationary model. Thus
it can be concluded that the prediction performance of
the proposed model can be relatively better than that
of the stationary model. However, Table 7 shows that
the coverage rate such that
ˆ
b
∗
≥ x
t
of stationary Pois-
son distribution is greater than that of the proposed
model. Therefore more precise predictions do not al-
ways help greater coverage rates.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
1000

6 CONCLUSION
This paper has proposed the credible interval predic-
tion algorithm of a nonstationary Poisson distribution
based on the Bayes decision theory. It is clarified that
the Bayes optimal credible interval prediction can be
uniquely obtained as the upper or lower percentile
points of the predictive distribution under a certain
loss function. Using real web traffic data, the perfor-
mances of the proposed algorithm is evaluated. The
upper limit of the credible interval prediction from the
proposed nonstationary Poisson distribution has rela-
tively smaller mean squared error by comparison with
the stationary Poisson distribution.
The loss function defined in this paper has been
restricted to the linear function. More generalized
classes of loss functions can be considered and those
would be future works.
REFERENCES
Berger, J. (1985). Statistical Decision Theory and Bayesian
Analysis. Springer-Verlag, New York.
Bernardo, J. M. and Smith, A. F. (2000). Bayesian Theory.
John Wiley & Sons, Chichester.
Harvey, A. C. (1989). Forecasting, Structural Time Series
Models and the Kalman Filter. Cambridge University
Press, Marsa, Malta.
Hogg, R. V., McKean, J. W., and Craig, A. T. (2013). Intro-
duction to Mathematical Statistics (Seventh Edition).
Pearson Education, Boston.
Koizumi, D., Matsushima, T., and Hirasawa, S. (2009).
Bayesian forecasting of www traffic on the time vary-
ing poisson model. In Proceeding of The 2009 In-
ternational Conference on Parallel and Distributed
Processing Techniques and Applications (PDPTA’09),
volume II, pages 683–389, Las Vegas, NV, USA.
CSREA Press.
Press, S. J. (2003). Subjective and Objective Bayesian
Statistics: Principles, Models, and Applications. John
Wiley & Sons, Hoboken.
Smith, J. Q. (1979). A generalization of the bayesian steady
forecasting model. Journal of the Royal Statistical So-
ciety - Series B, 41:375–387.
Weiss, L. and Blackwell, D. (1961). Statistical Decision
Theory. McGraw-Hill, New York.
Winkler, R. L. (1972). A decision-theoretic approach to in-
terval estimation. Journal of the American Statistical
Association, 67(337):187–191.
APPENDIX
A: Proof of Theorem 2.1
Note that time index t has been omitted for simplicity;
for example, θ
t
is written as θ, x
t
is written as x, and
so on. Suppose that data x are observed under the
parameter θ following Eq. (2). Then, according to
the Bayes theorem, the posterior distribution of the
parameter p

θ


x

is as follows:
p

θ


x

=
p

x


θ

p

θ


α,β

R
∞
0
p

x


θ

p

θ


α,β

dθ
=
β
α
Γ(α)x!
(θ)
α+x−1
exp[−(β + 1) θ]
β
α
Γ(α)x!
R
∞
0
(θ)
α+x−1
exp[−(β + 1) θ]dθ
=
(θ)
α+x−1
exp[−(β + 1) θ]
R
∞
0
(θ)
α+x−1
exp[−(β + 1) θ]dθ
. (36)
Then the denominator of the right-hand side in Eq.
(36) becomes,
Z
∞
0
(θ)
α+x−1
exp[−(β + 1) θ]dθ =
Γ(α + x)
(β + 1)
α+x
. (37)
Note that Eq. (37) is obtained by applying the fol-
lowing property of the gamma function.
Γ(x)
q
x
=
Z
∞
0
y
x−1
exp(−qy)wt . (38)
Substituting Eq. (37) in Eq. (36),
p

θ


x

=
(β + 1)
α+x
Γ(α + x)
(θ)
α+x−1
exp[−(β + 1) θ].(39)
Eq. (39) shows that the posterior distribution of
the parameter p

θ


x

also follows the gamma distri-
bution with parameters α +x,β + 1, which is the same
class of distribution as Eq. (3). This is the nature of
the conjugate family (Bernardo and Smith, 2000) for
the Poisson distribution.
Suppose the nonstationary transformation of the
parameter θ in Eq. (2). Similar transformation of pa-
rameters for the Beta distribution is discussed (Hogg
et al., 2013, pp. 162–163). According to Definition
2.6, the joint distribution p (θ,u) is the product of the
probability distributions of θ in Eq. (3) and u in Eq.
(5),
p(θ,u)
= p(θ) p (u)
=
(β)
α
Γ(kα)Γ[(1 −k)α]
(u)
kα−1
(1 − u)
(1−k)α−1
·(θ)
α−1
exp(−βθ) . (40)
Credible Interval Prediction of a Nonstationary Poisson Distribution based on Bayes Decision Theory
1001

Denote the two transformations as



v =
θu
k
;
w =
θ(1−u)
k
,
(41)
where θ > 0, 0 < u < 1, and 0 < k ≤ 1.
The inverse transformation of Eq. (41) becomes



θ = k (v + w);
u =
v
v+w
.
(42)
The Jacobian of Eq. (42) is
J =






∂θ
∂v
∂θ
∂w
∂u
∂v
∂u
∂w






=






k k
w
(v+w)
2
−
v
(v+w)
2






(43)
= −
k
v + w
= −
k
2
θ
6= 0. (44)
The transformed joint distribution p (v,w) is ob-
tained by substituting Eq. (42) for (40), and multi-
plying the right-hand side of Eq. (40) by the absolute
value of Eq. (43):
p(v, w)
=
(β)
α
Γ(kα) Γ [(1 − k) α]

v
v + w

kα−1
·

w
v + w

(1−k)α−1
[k (v + w)]
α−1
exp[−kb (v + w)]
=
(kβ)
α
Γ(kα) Γ [(1 − k) α]
(v)
kα−1
(w)
(1−k)α−1
·exp[−kβ(v + w)] .
(45)
Then, p (v) is obtained by marginalizing Eq. (45),
p(v) =
Z
∞
0
p(v, w)dw
=
(kβ)
α
(v)
kα−1
exp(−kβv)
Γ(kα)Γ[(1 −k)α]
·
Z
∞
0
(w)
(1−k)α−1
exp(−kβw)dw
=
(kβ)
α
(v)
kα−1
exp(−kβv)
Γ(kα)Γ[(1 −k)α]
Γ[(1 − k)α]
(kβ)
(1−k)α
=
(kβ)
kα
Γ(kα)
(v)
kα−1
exp(−kβv). (46)
Eq. (46) is obtained by applying the property of
gamma function in Eq. (38).
According to Eq. (46), v follows the gamma dis-
tribution with parameters kα,kβ.
Considering two Eqs. (39) and (46), it has been
proven that if the prior distribution of the scale param-
eter satisfies Θ ∼ Gamma(α,β), then its transformed
posterior distribution satisfies
Θ


x ∼ Gamma [k (α + x) ,k (β +1)] . (47)
By adding the omitted time index t, the recursive
relationships of the parameters of the gamma distri-
bution can be formulated as,

α
t+1
= k (α
t
+ x
t
);
β
t+1
= k (β
t
+ 1).
(48)
Thus, for t ≥ 2, the general α
t
,β
t
in terms of the
initial α
1
,β
1
can be written as







α
t
= k
t−1
α
1
+
t−1
∑
i=1
k
t−i
x
i
;
β
t
= k
t−1
β
1
+
t−1
∑
i=1
k
i−1
.
(49)
This completes the proof of Theorem 2.1. 2
B: Proof of Theorem 2.2
From Eqs. (1) and (7), the predictive distribution un-
der observation sequence x
x
x
t
becomes,
p

x
t+1


x
x
x
t

=
Z
∞
0
p

x
t+1


θ
t+1

p

θ
t+1


x
x
x
t

dθ
t+1
(50)
=
Z
∞
0

exp(−θ
t+1
)
x
t+1
!
(θ
t+1
)
x
t+1

·

(β
t+1
)
α
t+1
Γ(α
t+1
)
(θ
t+1
)
α
t+1
−1
exp(−β
t+1
θ
t+1
)

dθ
t+1
(51)
=
(β
t+1
)
α
t+1
(x
t+1
)!Γ(α
t+1
)
·
Z
∞
0
(θ
t+1
)
x
t+1
+α
t+1
−1
[−(β
t+1
+ 1) θ
t+1
]dθ
t+1
(52)
=
(β
t+1
)
α
t+1
(x
t+1
)!Γ(α
t+1
)
Γ(α
t+1
+ x
t+1
)
(β
t+1
+ 1)
α
t+1
+x
t+1
(53)
=
Γ(α
t+1
+ x
t+1
)
(x
t+1
)!Γ(α
t+1
)

β
t+1
β
t+1
+ 1

α
t+1

1
β
t+1
+ 1

x
t+1
.
(54)
Note that Eq. (52) is obtained by applying the prop-
erty of gamma function in Eq. (38).
This completes the proof of Theorem 2.2. 2
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
1002