Delay Predictors in Multi-skill Call Centers: An Empirical Comparison

with Real Data

Mamadou Thiongane

, Wyean Chan

and Pierre L’Ecuyer

Department of Mathematics and Computer Science, University Cheikh Anta Diop, Dakar, S

egal

Department of Computer Science and Operations Research, University of Montreal, Montr

eal QC, Canada, U.S.A.

Keywords:

Delay Prediction, Waiting Time, Automatic Learning, Neural Networks, Service Systems, Multi-skill Call

Centers.

Abstract:

We examine and compare different delay predictors for multi-skill call centers. Each time a new call (cus-

tomer) arrives, a predictor takes as input some observable information from the current state of the system,

and returns as output a forecast of the waiting time for this call, which is an estimate of the expected waiting

time conditional on the current state. Any relevant observable information can be included, e.g., the time of

the day, the set of agents at work, the queue size for each call type, the waiting times of the most recent calls

who started their service, etc. We consider predictors based on delay history, regularized regression, cubic

spline regression, and deep feedforward artiﬁcial neural networks. We compare them using real data obtained

from a call center. We also examine the issue of how to select the input variables for the predictors.

1 INTRODUCTION

In service systems such as call centers, medical clin-

ics, emergency services, and many others, announc-

ing to new arriving customers an accurate estimate

of their waiting time until the call is answered or the

service begins, immediately upon arrival, can be im-

prove the customer’s experience and satisfaction. For

ﬁrst-come ﬁrst-served systems with a single type of

customer and server, simple formulas are sometimes

available for the expected waiting time conditional on

the state of the system. But for more complex sys-

tems in which several types of customers share differ-

ent types of servers with certain priority rules (such as

in multi-skill call centers), computing good predictors

is generally much more difﬁcult, because for example

there are more sources of uncertainty and the condi-

tional waiting time distribution depends on a much

larger number of variables that determine the state of

the system. For instance, we may not know which

type of server will serve this customer, higher-priority

customers may arrive before the service starts, etc.

Proposed solutions to this problem are currently very

limited.

The aim of this paper is to examine different

learning-based delay predictors for multi-skill call

centers. We compare their effectiveness using real

data collected from a multi-skill call center. The pa-

rameters of the predictors are learned from part of this

data, and the rest of the data is used to measure the ac-

curacy of these delay predictors.

Most previous work on delay estimation was for

queueing systems with a single type of customer and

identical servers. The proposed methods for this case

can be classiﬁed in two categories: queue-length (QL)

predictors and delay-history (DH) predictors. A QL

predictor estimates the waiting time of a new arriving

customer with a function of the queue length when

this customer arrives. This function generally de-

pends on system parameters. In simple cases, with

exponential service times, it may correspond to an an-

alytical formula that gives the exact expected waiting

time conditional on the current state of the system;

see, e.g., Whitt (1999); Ibrahim and Whitt (2009a,

2010, 2011). A DH predictor, on the other hand, uses

the past customer delays to predict the waiting time

of a new arriving customer (Nakibly, 2002; Armony

et al., 2009; Ibrahim and Whitt, 2009b; Thiongane

et al., 2016; Dong et al., 2018). We discuss them in

Section 2.

There has been only limited work on developing

predictors for queueing systems with multiple types

of customers and multiple queues that can share some

servers, as in multi-skill call centers, in which each

server is an agent that can handle a subset of the call

types, and each call type has its own queue. The QL

100

Thiongane, M., Chan, W. and L’Ecuyer, P.

Delay Predictors in Multi-skill Call Centers: An Empirical Comparison with Real Data.

DOI: 10.5220/0009181401000108

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 100-108

ISBN: 978-989-758-396-4; ISSN: 2184-4372

predictors perform well in single-queue systems but

do not apply (and are very difﬁcult to adapt) to multi-

skill systems. The DH predictors can be used for

multi-skill systems but they often give large predic-

tion errors for those systems (Thiongane et al., 2016).

Senderovich et al. (2015) proposed predictors for

a multi-skill call center with multiple call types but a

single type (or group) of agents that can handle all

call types. Thiongane et al. (2015) proposed data-

based delay predictors that can be used for more gen-

eral multi-skill call centers or service systems. The

predicting functions were regression splines (RS) and

artiﬁcial neural network (ANN), and the input state

variables were the waiting time of the last customer of

the same type to have entered service, and the lengths

of some queues. The predictors were compared em-

pirically on small and simple simulation models, but

not on real data. In a similar vein, Ang et al. (2016)

studied the lasso regression (LR) method (Tibshirani,

1999) to predict waiting times in emergency (health-

care) departments, based on input variables such as

the queue length, and functions of them. Some of

these variables correspond to QL predictors that are

not directly applicable in the multi-skill setting. Nev-

ertheless, RL can be used in multi-skill call centers as

well, with appropriate input variables. In these paper,

the RS, LR, and ANN predictors are referred to as

machine learning (ML) delays predictors. Their per-

formance will depend largely on the input variables

considered. If important variables are left out, the

forecast may lose accuracy signiﬁcantly.

In this work, we compare the performances of RS,

LR, ANN, and various types of DH predictors, on real

data taken from an existing call center. The ANNs we

use are multilayer feed-forward neural networks. Our

main contributions are: (i) we propose a method to

select the relevant variables to predict the customers

wait times in multi-skill setting with the ML predic-

tors; (ii) we show the impact of leaving out some im-

portant input variables on the accuracy of ML predic-

tors; (iii) we test the accuracy of all these predictors

in a real multi-skill setting.

The remainder is organized as follows. In Section

2, we recall the deﬁnitions of various DH and ML

delay predictors. Section 3 describes the call center

and the data used for our experiments, and how we

have recovered the needed data that was not directly

available. Section 4 Numerical results are reported

and discussed in Section 5 contains a conclusion and

ﬁnal remarks.

2 DELAY PREDICTORS

In this section, we brieﬂy describe the DH and ML

delay predictors used in this work. We do not consider

the QL predictors in this work because they do not

apply in multi-skill settings.

2.1 DH Predictors

DH predictors use past customer delays to predict

the waiting time of a newly arriving customer. They

do not require a learning phase to optimize several

parameters and they are easy to implement in prac-

tice. The DH predictors considered here are the best

performers on experiments with simulated system,

among those we found in the literature. They are de-

ﬁned as follows.

Last-to-Enter-Service (LES). This predictor re-

turns the wait time experienced by the customer of the

same class who was the last enter the system, among

those who had to wait and have started their service

(Ibrahim and Whitt, 2009b). It is the most popular

DH predictor.

Average LES (Avg-LES). This one returns the av-

erage delay experienced by the N (a ﬁxed integer)

most recent customers of the same class who entered

service after waiting a positive time. It is often used

in practice (Dong et al., 2018).

Average LES Conditional on Queue Length

(AvgC-LES). This one returns an average of the

wait times of past customers of the same class who

found the same queue length when they arrived. It

was introduced in (Thiongane et al., 2016) and was

the best performing DH predictor in some experi-

ments with simulated systems in that paper.

Extrapolated LES (E-LES). For a new customer

of class j, this predictor use the delay information

of all customers of the same class that are currently

waiting in queue. The ﬁnal wait times of these cus-

tomers are still unknown, but the elapsed (partial) de-

lays are extrapolated to predict the ﬁnal delays of all

these customers, and E-LES returns a weighted av-

erage of these extrapolated delays (Thiongane et al.,

2016).

Proportional Queue LES (P-LES). P-LES read-

justs the time delay x of the LES customer to account

for the difference in the queue length seen by the LES

and the new arriving customer (Ibrahim et al., 2016).

Delay Predictors in Multi-skill Call Centers: An Empirical Comparison with Real Data

101

If Q

LES

denotes the number of customers in queue

when the LES customer arrived, and Q the number

of customers in queue ahead of the new arrival, the

waiting time of this new customer is predicted by

D = x

Q + 1

LES

+ 1

2.2 ML Delay Predictors

The idea behind ML predictors is to approximate the

conditional expectation of the waiting time W of an

arriving customer of type k, conditional on all ob-

servable state variables of the system at that time, by

some predictor function of selected observable vari-

ables deemed important. We denote by x the values

of these selected (input) variables, and the prediction

is F

k,θ

(x) where F

k,θ

is the predictor function for call

type k, which depends on a vector of parameters θ,

which is learned from data in a preliminary training

step.

In a simple system such as a GI/M/s queue, the

relevant state variables are the number of customers

in queue, the number s of servers, and the service rate

µ. But for more complex multi-skill centers, identify-

ing the variables that are most relevant to estimate the

expected waiting time for a given customer type k can

be challenging.

In our experiments, we proceed as follows. We

ﬁrst include all observable state variables that might

have an inﬂuence on the expected waiting time. Then

we make a selection by using a feature-selection

method which provides an “importance” score for

each variable in terms of its estimated predictive

power. The variables are then ranked according to

these scores, and those with sufﬁciently high scores

are selected. Estimating relevant predictive-power

scores for a large number of candidate variables is

generally difﬁcult. In our work, we do this with the

Boruta feature selection algorithm (Kursa and Rud-

nicki, 2010), which was the best performer among

several feature selection algorithms compared by De-

genhardt et al. (2017).

Boruta is actually a wrapper built over the random

forest algorithm proposed by Breiman (2001), which

uses bootstrapping to generate a forest of several deci-

sion trees. In our setting, each node in a decision tree

corresponds to a selection decision for one input vari-

able. Boruta ﬁrst extends the data by adding copies

of all input variables, and shufﬂes these variables to

reduce their correlations with the response. These

shufﬂed copies are called shadow features. Boruta

runs a random forest classiﬁer on the extended data

set. Trees are independently developed on different

bagging (bootstrap) samples of the training set. The

importance measure of each attribute (i.e., input vari-

able) is obtained as the loss of accuracy of the model

caused by the random permutation of the values of

this attribute across objects (the mean decrease accu-

racy). This measure is computed separately for all

trees in the forest that use a given attribute. Then, for

each attribute, the average and standard deviation of

the loss of accuracy is computed, a Z score is com-

puted by dividing the average loss by its standard de-

viation, and the latter is used as the importance mea-

sure. The maximum Z-score among the shadow fea-

tures (MZSA) are used to determine which variables

are useful to predict the response (i.e., the waiting

time). The attributes whose Z-scores are signiﬁcantly

lower than MZSA is declared “unimportant”, those

whose Z-scores are signiﬁcantly higher than MZSA

as declared “important” (Kursa and Rudnicki, 2010),

and decisions about the other ones are made using

other rules.

In this study, our candidate input variables are the

queue length for all call types (r is the vector of these

queues length, and the queue length for call type T1

to T5 are named q1 to q5 respectively), the number s

of agents that are serving the given call type, the total

number n of agents currently working in the system,

the arrival time t of the arriving customer, the wait

time of the N most recently served customers of the

given call type (they are named LES1, LES2,... , and

l is the vector of these waiting times), and the wait-

ing time predicted by the DH predictors LES, P-LES,

E-LES, Avg-LES, and AvgC-LES (d the vector that

contains these predicted waiting times).

We consider three ways of deﬁning the predic-

tor function F

k,θ

: (1) a smoothing (least-squares re-

gression) cubic spline which is additive in the input

variables (RS), (2) a lasso (linear) regression (LR),

and (3) a deep feedforward multilayer artiﬁcial neural

network (ANN). The parameter vector θ is selected

in each case by minimizing the mean squared error

(MSE) of predictions. That is, if E = F

k,θ

(x) is the

predicted delay for a “random” customer of type k

who receives service after some realized wait time W ,

then the MSE for type k calls is

MSE

= E[(W −E)

We cannot compute this MSE exactly, so we estimate

it by its empirical counterpart, the average squared

error (ASE), deﬁned as

ASE

∑

c=1

k,c

−E

k,c

)

(1)

for customer type k, where C

is the number of served

customers of type k who had to wait in queue. We will

in fact use a normalized version of the ASE, called the

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

102

root relative average squared error (RRASE), which

is the square root of the ASE divided by the average

wait time of the C

served customers, rescaled by a

factor of 100:

RRASE =

√

ASE

(1/C

)

∑

c=1

k,c

×100.

We perform this estimation of the parameter vector

θ with a learning data set that represent 80% of the

collected data. The other 20% is used to measure and

compare the accuracy of these delay predictors.

2.2.1 Regression Splines (RS)

Regression splines are a powerful class of approxima-

tion methods for general smooth functions (de Boor,

1978; James et al., 2013; Wood, 2017). Here we use

smoothing additive cubic splines, for which the pa-

rameters are estimated by least-squares regression af-

ter adding a penalty term on the function variation to

favor more smoothness. If the information vector is

written as x = (x

,.. .,x

), the additive spline predic-

tor can be written as

k,θ

(x) =

∑

d=1

where each f

is a one dimensional cubic spline. The

parameters of all these spline functions f

form the

vector θ. We estimated these parameters using the

function gam from the R package mgcv (Wood, 2019).

2.2.2 Lasso Regression (LR)

Lasso Regression is a type of linear regression (Tib-

shirani, 1996; James et al., 2013; Friedman et al.,

2010) in which a penalty term equal to the sum of ab-

solute values of the magnitude of coefﬁcients is added

before minimizing the mean squared error, to reduce

over-ﬁtting. If the input vector is x = (x

,.. .,x

), the

lasso regression predictor can be written as

k,θ

(x) =

∑

d=1

·x

+ λ.

One can estimate the parameters by using the function

glmnet from the R package gmlnet (Friedman et al.,

2019).

2.2.3 Deep Feed-forward Artiﬁcial Neural

Network (ANN)

A deep feedforward artiﬁcial neural network is an-

other very popular and effective way to approxi-

mate complicated high-dimensional functions (Ben-

gio et al., 2012; LeCun et al., 2015). This type of neu-

ral network has one input layer, one output layer, and

several hidden layers. The outputs of nodes at layer l

are the inputs of every node at the next layer l +1. The

number of nodes at the input layer is equal to the num-

ber of elements in the input vector x, and the output

layer has only one node which returns the estimated

delay. For each hidden node, we use a rectiﬁer acti-

vation function, of the form h(z) = max(0,b + w ·z),

in which z is the vector of inputs for the node, while

the intercept b and the vector of coefﬁcients w are pa-

rameters learned by training (Glorot et al., 2011). For

the output node in the output layer (which return the

estimated delay), we use a linear activation function,

h(z) = b + w ·z, in which z is the vector of outputs

from the nodes at the last hidden layer. The (large)

vector θ is the set of all these parameters b and w, over

all nodes. These parameters are learned by a back-

propagation algorithm that uses a stochastic gradient

descent method. Many other parameters and hyper-

parameters used in the training have to be determined

empirically. For a guide on training, see Bergstra and

Bengio (2012); Bengio (2012); Gulcehre and Bengio

(2016); Goodfellow et al. (2016). To train our ANNs

(i.e., estimate the vectors θ), we used the Pylearn2

software Goodfellow et al. (2013).

3 THE CALL CENTER AND

AVAILABLE DATA

We performed an empirical study using data from a

real multi-skill call center from the VANAD labora-

tory group, located in Rotterdam, in The Netherlands.

This center operates from 8 a.m to 8 p.m from Mon-

day to Friday. It handles 27 call types and has 312

agents. Each agent has a set of skills, which cor-

responds to a subset of the call types. The routing

mechanism works as follows. When a call arrives,

the customer ﬁrst interacts with the IVR (interactive

voice response unit) to choose the call type. If there is

an available agent with this skill, the call is assigned

to the longest idle agent among those. Otherwise, the

call joins an invisible FCFS (ﬁrst come ﬁrst served)

queue.

The call log data has 1,543,164 calls recorded

over one year, from January 1 to December 31, 2014.

About 56% of those calls are answered immediately,

38% are answered after some wait, and about 6%

abandon. In this study, we consider only the ﬁve call

types with the largest call volume. They account for

more than 80% of the total volume. Table 1 gives a

statistical summary of the arrival counts for these ﬁve

call types, named T1 to T5. It also gives the average

waiting time (AWT), average service time (AST), and

average queue size (AQS) for each one. The other call

Delay Predictors in Multi-skill Call Centers: An Empirical Comparison with Real Data

103

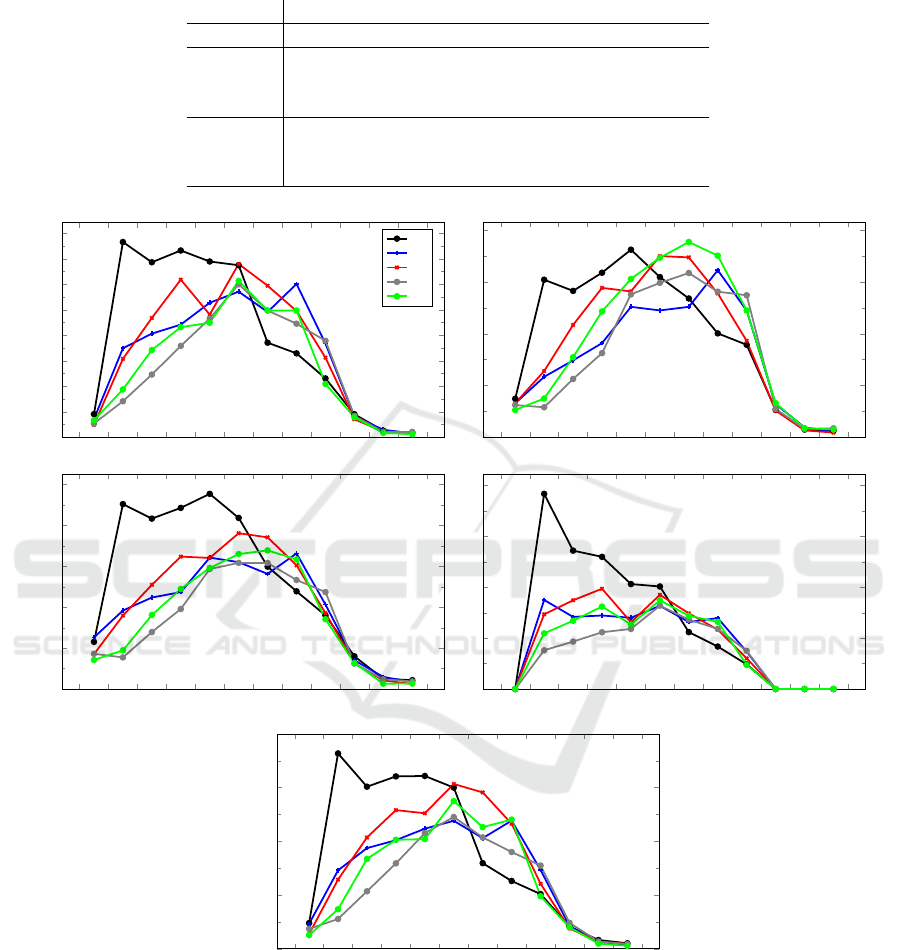
Table 1: Arrival counts and statistical summary for the ﬁve selected call types over the year. The AWT and AST

are in seconds.

T1 T2 T3 T4 T5

Number 568 554 270 675 311 523 112 711 25 839

No wait 61% 52% 55% 45% 34%

Wait 35% 40% 40% 46% 54%

Abandon 4% 7% 5% 8% 12%

AWT 77 91 83 85 110

AST 350 308 281 411 311

AQS 8.2 3.3 4.4 4.3 0.9

8 9 10 11 12 13 14

15 16

17 18 19 20

100

120

140

160

Period of 1 hour (call type T1)

Mean arrival counts

8 9 10 11 12 13 14

15 16

17 18 19 20

Period of 1 hour (call type T2)

Mean arrival counts

8 9 10 11 12 13 14

15 16

17 18 19 20

100

Period of 1 hour (call type T3)

Mean arrival counts

8 9 10 11 12 13 14

15 16

17 18 19 20

Period of 1 hour (call type T4)

Mean arrival counts

8 9 10 11 12 13 14

15 16

17 18 19 20

Period of 1 hour (call type T5)

Mean arrival counts

Figure 1: Average arrival counts per hour and per call type, for each type of day, over the year.

types, not considered here, accounted for less than

10 000 calls altogether during the year. Each one had

less than 30 calls a day on average. We do not study

delay predictors for them.

Figure 1 shows the average number of arrivals per

hour per call type, for each day of the week, over the

year. We see from this ﬁgure that the arrival behavior

for Monday differs signiﬁcantly from that of the other

days, especially in the morning. A plausible explana-

tion for this is that Monday is the ﬁrst day of the week

and the center is closed on the two previous days. This

means that it would make sense to develop two sepa-

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

104

0 50 100 150 200 250 300

0.000

0.002 0.004 0.006 0.008 0.010

Waiting time (sec)

Density

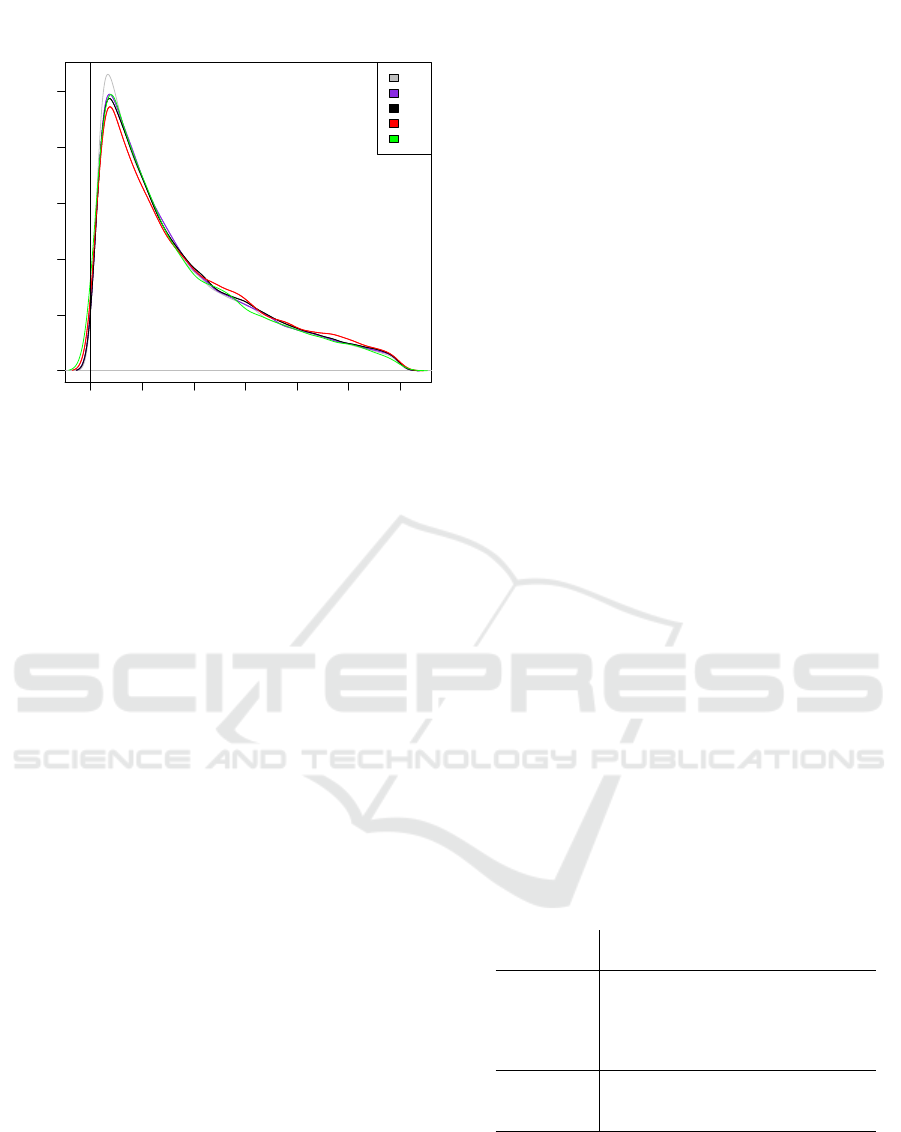
Figure 2: Waiting time density for calls who waited and

were served, per call type.

rate sets of predictors: one for Monday’s and one for

the other days. In this paper, we focus on the other

days (Tuesday to Friday). Figure 2 shows a density

estimate of the waiting time for calls who waited and

did not abandon, for the ﬁve considered call types.

These densities were estimated using kernel density

estimators with a normal kernel. This explains the

fact that part of the density near zero “leaks” to the

negative side. The true density starts at zero.

The data contains the following information on

each call received in the one-year period: the call

type, the arrival time, the date, the desired service, and

the VRU entry and exit time. There is also a queue en-

try time and a queue exit time, but only for the calls

that have to wait. For those calls, we also know if

they received service or abandoned. Finally, for the

called that were served, we have the times when ser-

vice started and when it ended, and we can easily

compute the realized waiting time of the call.

For the ML predictors, when a call arrives, we

need to observe a large number of candidate input

variables (features) in x = (r,s, n,l,d,t) that are re-

quired to predict the waiting time of this call. How-

ever, most of this information is not directly available

in the data. Similarly, much of the information re-

quired for the DH predictors is not directly observ-

able in the historical data. To address this issue, we

had to build a simulator that could replay the history

from the available data and compute all this miss-

ing information (e.g., the detailed state of the sys-

tem each time a customer arrives, the LES, Avg-LES,

etc.). This simulator was implemented in Java using

the simevent package of the SSJ simulation library

(L’Ecuyer et al., 2002; L’Ecuyer, 2016).

4 NUMERICAL EXPERIMENTS

4.1 Identifying the Important Input

Variables

After reconstructing the detailed data, we ran the

Boruta algorithm on the data set for each call type

to identify the candidate variables that are important

to predict the waiting time. As an illustration of the

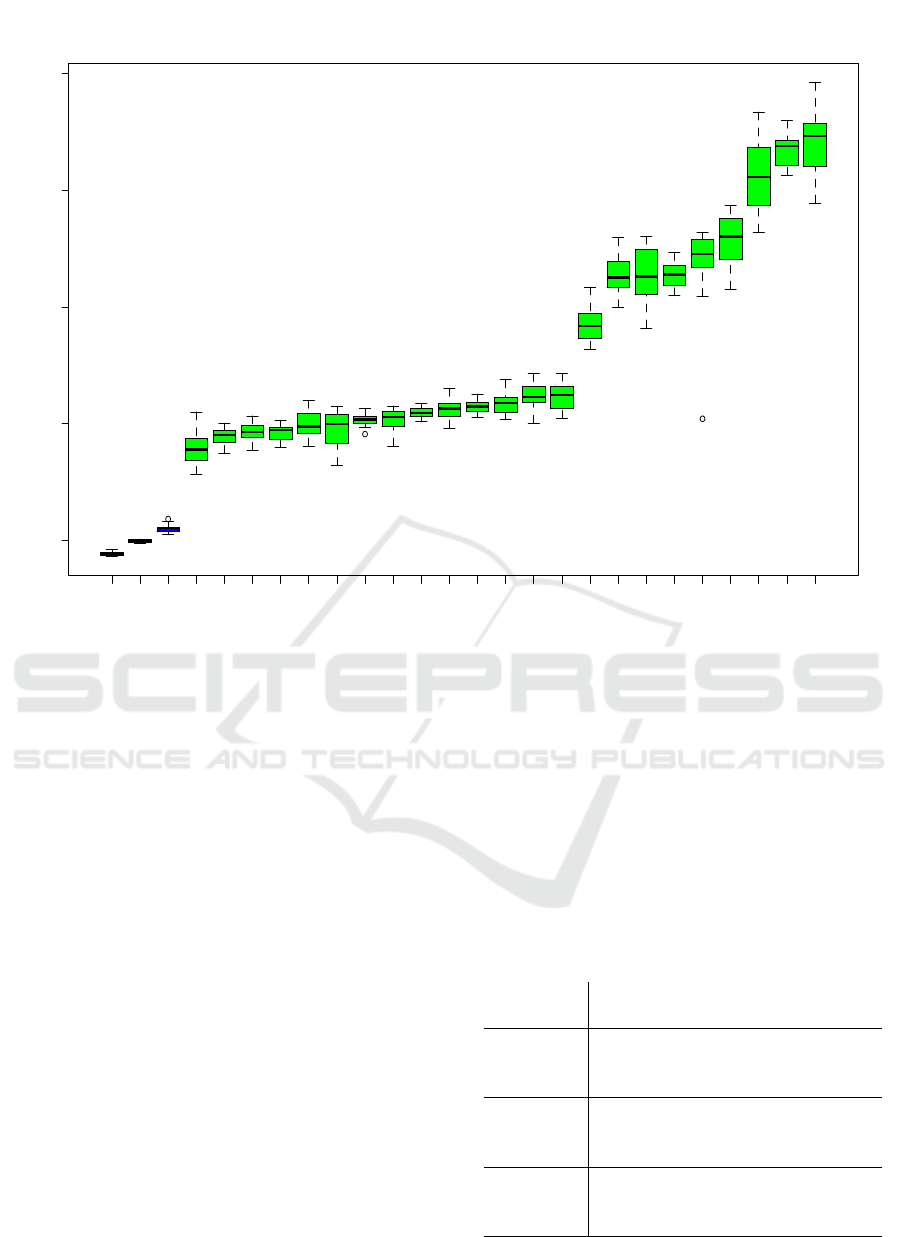
results, Figure 3 reports the importance scores of the

input variables for call type T1. It shows a box plot of

the Z-scores of all the attributes (input variables), plus

the minimum, the average, and the maximum shadow

scores. All the candidate variables have their box-

plots (in green) much higher than the shadow scores,

which means that they are all declared “important”

by Boruta. The same was observed for all other call

types.

We also see in the ﬁgure that the most important

input variables to predict waiting times (those with the

highest Z-scores) for call type T1 are (in this order)

the arrival time t of the call, the queues length, the

prediction of AvgC-LES, the total number n of agents

in the system, and the number s of agents serving this

call type. The other variables have a lower score.

We then made an experiment to see if removing all

these lower-score input variables from the selected in-

puts would make a difference in prediction accuracy,

and found no signiﬁcant difference (less than 0.1% in

all cases). Therefore, we decided not to include them

as input variables when comparing our predictors (in

the next subsection).

4.2 RRASE with Delay Predictors

Table 2: RRASE of delay predictors.

Call Types

Predictors T1 T2 T3 T4 T5

Avg-LES 48.9 61.0 56.7 48.7 69.7

LES 44.3 57.7 51.8 44.5 66.1

AvgC-LES 44.3 56.5 51.6 42.4 62.4

E-LES 63.7 65.4 64.0 58.8 77.5

P-LES 71.2 70.5 71.4 68.5 80.3

RS 39.6 49.2 45.5 39.5 50.1

RL 41.5 51.5 47.1 38.5 51.7

ANN 36.1 46.2 44.8 37.7 48.7

Here we compare the different delay predictors in

terms of RRASE, for each call type. For all the ML

predictors, our vector of selected input variables was

x =(t, q1, q2, q3, q4, q5, n, s, LES, AvgC-LES). Table

2 reports the RRASEs. We ﬁnd that the ML predic-

tors perform signiﬁcantly better than the DH predic-

tors in all cases, and that the best performer is ANN.

Delay Predictors in Multi-skill Call Centers: An Empirical Comparison with Real Data

105

0 20 60 80

Importance

sh. Min

sh.Mean

sh. Max

E-LES

P-LES

LES9

LES10

LES6

Avg-LES

LES5

LES3

LES4

LES7

LES8

LES2

LES1

LES

AvgC-LES

Figure 3: Box plot of score of variable importance.

Among the DH predictors, AvgC-LES is the best per-

former, and it is closely followed by LES and Avg-

LES. E-LES was the second best DH predictors in

previous experiments with simulated systems (Thion-

gane et al., 2016), but it does not perform well with

this real data. P-LES also performs very poorly.

4.3 Impact of Leaving Out Important

Input Variables

We made some empirical experiments to study the

impact of leaving out some input variables deemed

important by Boruta, for the ML predictors. In par-

ticular, we want to compare our ML predictors with

those proposed by Thiongane et al. (2015), for which

some of the input variables considered here were not

present. We ﬁrst remove the arrival time t and the pre-

dicted delay with AvgC-LES from the input variables.

We name the ML predictors without these two vari-

ables as RS-2, LR-2, and ANN-2. Then, in addition

to the two previous variables, we also remove a queue

length for a call type that differs arriving call. We

name the resulting ML predictors RS-3, LR-3, and

ANN-3. Note that none of those three input variables

are included in x as input variables by Thiongane et al.

(2015).

Table 3 shows the RRASE of these “weakeaned”

predictors. We ﬁnd that removing the ﬁrst two fea-

tures reduces signiﬁcantly the accuracy of ML pre-

dictors, and removing an additional one reduces the

accuracy further, again signiﬁcantly. Thus, at least

for this call center, our ML predictors are more accu-

rate than those proposed by Thiongane et al. (2015).

This shows that the choice of input variables is very

important when building ML predictors.

Table 3: RRASE of delay predictors.

Call Types

Predictors T1 T2 T3 T4 T5

RS 39.6 49.2 45.5 39.5 50.1

LR 41.5 51.5 47.1 38.5 51.7

ANN 36.1 46.2 44.8 37.7 48.7

RS-2 41.9 52.0 47.7 40.9 52.5

LR-2 43.9 54.0 49.1 39.2 53.1

ANN-2 39.7 49.2 46.9 38.5 50.3

RS-3 42.5 53.0 47.9 41.2 52.9

LR-3 44.3 55.4 50.7 39.8 54.0

ANN-3 40.4 50.2 47.0 38.7 50.9

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

106

5 CONCLUSION

We have examined and compared several DH and ML

delay predictors on data from a real multi-skill call

center. We found that the ML predictors are much

more accurate than the DH predictors. Within the ML

predictors, ANN was more accurate than RS and LR,

but the latter can be trained much faster than ANN,

and could be more accurate when the amount of avail-

able data is smaller. We saw the negative impact of

leaving out relevant input variables on the accuracy

of the ML predictors, and illustrated how well Boruta

can identify the most relevant input variables. In on-

going work, we want to develop effective methods to

predict and announce not only a point estimate of the

waiting time, but an estimate of the entire conditional

distribution of the delay.

ACKNOWLEDGEMENTS

This work has been supported by grants from

NSERC-Canada and Hydro-Qu

ebec, and a Canada

Research Chair to P. L’Ecuyer. We thank Ger Koole,

from VU Amsterdam, who provided the data.

REFERENCES

Ang, E., Kwasnick, S., Bayati, M., Plambeck, E., and Ara-

tow, M. (2016). Accurate emergency department wait

time prediction. Manufacturing & Service Operations

Management, 18(1):141–156.

Armony, M., Shimkin, N., and Whitt, W. (2009). The im-

pact of delay announcements in many-server queues

with abandonments. Operations Research, 57:66–81.

Bengio, Y. (2012). Practical recommendations for gradient-

based training of deep architectures. Neural Net-

works: Tricks of the Trade, 7700:437–478.

Bengio, Y., Courville, A. C., and Vincent, P. (2012). Unsu-

pervised feature learning and deep learning: A review

and new perspectives. CoRR, abs/1206.5538:1–30.

Bergstra, J. and Bengio, Y. (2012). Random search for

hyper-parameter optimization. Journal of Machine

Learning Research, 13:281–305.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

de Boor, C. (1978). A Practical Guide to Splines. Num-

ber 27 in Applied Mathematical Sciences Series.

Springer-Verlag, New York.

Degenhardt, F., Seifert, S., and Szymczak, S. (2017). Evalu-

ation of variable selection methods for random forests

and omics data sets. Brieﬁngs in Bioinformatics,

20(2):492–503.

Dong, J., Yom Tov, E., and Yom Tov, G. (2018). The im-

pact of delay announcements on hospital network co-

ordination and waiting times. Management Science,

65(5):1949–2443.

Friedman, J., Hastie, T., and Tibshirani, R. (2010). Regular-

ization paths for generalized linear models via coordi-

nate descent. Journal of Statistical Software, 33(1):1–

22.

Friedman, J., Hastie, T., Tibshirani, R., Narasimhan,

B., Simon, N., and Qian, J. (2019). R Pack-

age glmnet: Lasso and Elastic-Net Regularized

Generalized Linear Models. https://CRAN.R-

project.org/package=glmnet.

Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse

rectiﬁer neural networks. In Gordon, G., Dunson,

D., and Miroslav, editors, Proceedings of the Four-

teenth International Conference on Artiﬁcial Intelli-

gence and Statistics, volume 15 of Proceedings of Ma-

chine Learning Research, pages 315–323, Fort Laud-

erdale, FL, USA. PMLR.

Goodfellow, I., Bengio, Y., and Courville, A.

(2016). Deep Learning. MIT Press.

http://www.deeplearningbook.org.

Goodfellow, I., Warde-Farley, D., Lamblin, P., Dumoulin,

V., Mirza, M., Pascanu, R., Bergstra, J., Bastien, F.,

and Bengio, Y. (2013). Pylearn2: A machine learning

research library.

Gulcehre, C. and Bengio, Y. (2016). Knowledge mat-

ters: Importance of prior information for optimization.

Journal of Machine Learning Research, 17:1–32.

Ibrahim, R., L’Ecuyer, P., Shen, H., and Thiongane, M.

(2016). Inter-dependent, heterogeneous, and time-

varying service-time distributions in call centers. Eu-

ropean Journal of Operational Research, 250:480–

492.

Ibrahim, R. and Whitt, W. (2009a). Real-time delay es-

timation based on delay history. Manufacturing and

Services Operations Management, 11:397–415.

Ibrahim, R. and Whitt, W. (2009b). Real-time delay estima-

tion in overloaded multiserver queues with abandon-

ments. Management Science, 55(10):1729–1742.

Ibrahim, R. and Whitt, W. (2010). Delay predictors for cus-

tomer service systems with time-varying parameters.

In Proceedings of the 2010 Winter Simulation Confer-

ence, pages 2375–2386. IEEE Press.

Ibrahim, R. and Whitt, W. (2011). Real-time delay esti-

mation based on delay history in many-server service

systems with time-varying arrivals. Production and

Operations Management, 20(5):654–667.

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2013).

An Introduction to Statistical Learning, with Applica-

tions in R. Springer-Verlag, New York.

Kursa, M. B. and Rudnicki, W. R. (2010). Feature selec-

tion with the boruta package. Journal of Statistical

Software, 36:1–13.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. Nature, 521:436–444.

L’Ecuyer, P. (2016). SSJ: Stochastic simulation in Java.

http://simul.iro.umontreal.ca/ssj/.

L’Ecuyer, P., Meliani, L., and Vaucher, J. (2002). SSJ:

A framework for stochastic simulation in Java. In

ucesan, E., Chen, C.-H., Snowdon, J. L., and

Charnes, J. M., editors, Proceedings of the 2002

Delay Predictors in Multi-skill Call Centers: An Empirical Comparison with Real Data

107

Winter Simulation Conference, pages 234–242. IEEE

Press.

Nakibly, E. (2002). Predicting waiting times in telephone

service systems. Master’s thesis, Technion, Haifa, Is-

rael.

Senderovich, A., Weidlich, M., Gal, A., and Mandelbaum,

A. (2015). Queue mining for delay prediction in

multi-class service processes. Information Systems,

53:278–295.

Thiongane, M., Chan, W., and L’Ecuyer, P. (2015). Waiting

time predictors for multiskill call centers. In Proceed-

ings of the 2015 Winter Simulation Conference, pages

3073–3084. IEEE Press.

Thiongane, M., Chan, W., and L’Ecuyer, P. (2016). New

history-based delay predictors for service systems. In

Proceedings of the 2016 Winter Simulation Confer-

ence, pages 425–436. IEEE Press.

Tibshirani, R. (1996). Regression shrinkage and selection

via the LASSO. Journal of the Royal Statistical Soci-

ety, Series B (Methodological), pages 267–288.

Tibshirani, R. (1999). Regression shrinkage and selection

via the lasso. Journal of the Royal Statistical Society,

7(0):267–288.

Whitt, W. (1999). Predicting queueing delays. Management

Science, 45(6):870–888.

Wood, S. N. (2017). Generalized Additive Models: An In-

troduction with R. Chapman and Hall / CRC Press,

Boca Raton, FL, second edition.

Wood, S. N. (2019). R Package mgcv: Mixed GAM Compu-

tation Vehicle with Automatic Smoothness Estimation.

https://CRAN.R-project.org/package=mgcv.

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

108