Production Scheduling based on Deep Reinforcement Learning using

Graph Convolutional Neural Network

Takanari Seito and Satoshi Munakata

Hitachi Solutions East Japan, Ltd., Japan

Keywords: Production Scheduling, Deep Reinforcement Learning, Graph Convolutional Neural Network.

Abstract: While meeting frequently changing market needs, manufacturers are faced with the challenge of planning

production schedules that achieve high overall performance of the factory and fulfil the high fill rate constraint

on shop floors. Considerable skill is required to perform the onerous task of formulating a dispatching rule

that achieves both goals simultaneously. To create a useful rule independent of human expertise, deep

reinforcement learning based on deep neural networks (DNN) can be employed. However, conventional

DNNs cannot learn the important features needed for meeting both requirements because they are unable to

process qualitative information included in these schedules, such as the order of operations in each resource

and correspondence between allocated operations and resources. In this paper, we propose a new DNN model

that can extract features from both numeric and nonnumeric information using a graph convolutional neural

network (GCNN). This is done by applying schedules as directed graphs, where numeric and nonnumeric

information are represented as attributes of nodes and directed edges, respectively. The GCNN transforms

both types of information into the feature values by transmitting and convoluting the attributes of each

component on a directed graph. Our investigation shows that the proposed model outperforms the

conventional one.

1 INTRODUCTION

In recent years, consumers’ needs have diversified,

while the life cycles of products have shortened.

Under these conditions, there are two issues in

manufacturing industries for large-item small-volume

production: First, the issues for managers to shorten

the lead time (LT) from material input to product

shipment and strengthen the ability to respond to

short delivery time. Second, the issue for shop floors

to perform efficiently subject to individual constraints

for each product and production line. It is important

for manufacturing industries to construct a production

schedule that satisfies both managers and shop floors.

To make a production schedule, we use a general

dispatching method (Pinedo, 2012), which makes

schedules by successively allocating operations to

resources based on dispatching rules. A dispatching

rule is a criterion for selecting a remaining operation

and a capable resource. Due to the simplicity of the

existing rules, scheduling staff modify them so that a

schedule satisfies both managers and shop floors, e.g.,

by combining multiple rules and/or adding individual

constraints to the rules. However, to construct a good

rule, we need trial and error based on experiences and

expertise of scheduling staff. Therefore, this work can

be a significant burden. Nowadays, due to labor

shortage, especially in Japan, it is difficult to transfer

the expertise to new staff. Thus, to reduce work load,

we need a technology that automatically constructs a

dispatching rule.

For the automatic construction of a dispatching

rule, Riedmiller et al. (1999) applied deep

reinforcement learning (DRL) to production

scheduling. DRL is a machine learning method that

learns a policy that selects an action for each state

through trial and error. In the application of DRL to

production scheduling, we make many schedules by

using the learnt rule at that time and update the rule

to select a good allocation.

In DRL, a dispatching rule is implemented as a

DNN. The DNN receives a state of schedule-making

and computes the probabilistic values for candidates

of allocations. To construct a good schedule that

satisfies both managers and shop floors, it is

necessary for the DNN to extract two types of

information: the factory’s overall performance and

the fill rate constraint. However, the conventional

DNN does not extract the latter, e.g., the resource

766

Seito, T. and Munakata, S.

Production Scheduling based on Deep Reinforcement Learning using Graph Convolutional Neural Network.

DOI: 10.5220/0009095207660772

In Proceedings of the 12th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2020) - Volume 2, pages 766-772

ISBN: 978-989-758-395-7; ISSN: 2184-433X

each operation is allocated to and the kind of

operations allocated before or after. Therefore, a

conventional DNN cannot be used to make a schedule

that satisfies both managers and shop floors.

In this paper, we propose a new DNN model that

can deal with both types of information. This model

is based on the following two concepts: 1) a schedule

can be represented as a graph structure and 2) a

feature value of each node on the graph can be

extracted by GCN.

The remainder of this paper is structured as

follows. In section 2, we define the problem and

production scheduling. In section 3, we explain the

method of application of DRL to production

scheduling and present the gaps in previous studies.

In section 4, we propose a method to overcome the

issue. In section 5 and 6, we present the experimental

setup and the results. In section 7, we present the

conclusion and future directions of research.

2 PRODUCTION SCHEDULING

In this paper, we deal with a job shop scheduling

problem (JSP) (Pinedo, 2012) that models large-item

small-volume production and add a practical

extension to it. In a practical setting of the

manufacturing industries, there are master data that

define what can be produced and the orders are

selected from the master data accordingly. To follow

this setting, we define master data (mst for short) and

artificially create a problem from it: transaction data

(trn for short).

Master data is given as sets of  items [itm

, …,

itm

] (itm for short) and  resources [rsc

, …, rsc

]

(rsc for short). An item consists of  processes [prc

…, prc

] (prc for short). A process requires

processing time and one capable resource.

Transaction data is given as a set of  jobs [job

, …,

job

]. A job is related to an item and should perform

all processes of the item. We call these processes

operations (opr for short). An operation should be

allocated to a capable resource of a related process

and follow a sequence of the process.

Algorithm 1: Deep Reinforcement Learning.

1. create 



training problems

2. for 



1,⋯,



3. for each training problem:

4. make 



schedules by EG with 

5. select the best schedule

6. update the DNN with selected schedules

7. ←Δ

3 DEEP REINFORCEMENT

LEARNING

3.1 Application to Scheduling

To generate a dispatching rule automatically,

Riedmiller et al. (1999) proposed an approach using

DRL. DRL applied to production scheduling

generates a dispatching rule through trials and errors

by repeatedly 1) making many schedules using the

learnt rule at that time to obtain better supervised

allocations and 2) updating the rules to select the

supervised allocations.

In DRL, we make a schedule by successively

allocating operations like in a dispatching method,

but it differs from a dispatching method in that we use

a DNN as a dispatching rule. A DNN receives a state

of schedule-making and computes a policy, which is

a set of probabilistic values for candidates of

allocations. We select an allocation from the

candidates that maximize the probabilistic value. A

good schedule can be made by increasing the

probabilistic value of a good allocation.

We show a general DRL algorithm in Algorithm

1. To construct a dispatching rule that makes a good

schedule for several problems, we prepare 



training problems from the master data. The

algorithm consists of two phases and repeat it 



times.

In the first phase, we make 



schedules for

each training problem to obtain better supervised

allocations by using an epsilon-greedy method (EG).

For each scheduling step, we select an allocation by

using the learned DNN or randomly with a

probability 1 or  . The search ratio  is

initialized to 



and updated to Δ at the end of a

training step.

In the second phase, we update the DNN so as to

increase the probabilistic values of supervised

allocations obtained in the previous phase. To reduce

computational time and learn the best allocations, we

select one schedule for each training problem that

maximizes the value of a schedule. For each selected

schedule and each scheduling step, we evaluate an

error between an output of the DNN and a supervised

allocation by a mean-squared error criterion (MSE)

with one-hot representation and minimize them by

Adam (Kingma et al., 2014) with default hyper

parameters. (Although it is better to use a cross-

entropy error criterion for the one-hot representation

in general, we extracted better ability of the DNN in

the MSE.)

Production Scheduling based on Deep Reinforcement Learning using Graph Convolutional Neural Network

767

3.2 Issues in Previous Studies

As mentioned in section 1, planning production

schedules to satisfy the requirements of both factory

management and operations is an urgent problem for

manufacturers. When making schedules,

manufacturers have to simultaneously consider the

factory’s overall performance and the fill rate

constraint on shop floors.

In the DRL framework, we construct a reward

function based on the information to learn a better

policy of allocating operations by repeatedly making

trial production schedules and evaluating them. As

such, it is necessary for a DNN to extract feature

values that include both the information from the trial

schedules satisfactorily. In general, it is easy to create

a DNN model that deals with feature values of the

factory’s overall performance as they are usually

presented as numeric indices such as LT and

availability. On the other hand, conventional DNN

models, which are used in previous studies

(Riedmiller et al., 1999; Zhang et al., 1995; Gabel et

al., 2008), cannot extract feature values characterized

by the satisfaction of the fill rate constraint. This is

because such feature values are comprised of

nonnumeric information about the schedules such as

the resource each operation is allocated to and the

kind of operations allocated before or after. It is

difficult for a DNN model to accept the

abovementioned nonnumeric information as input

and transform them into feature values.

For example, Riedmiller et al. (1999) used only

numeric information to extract feature values of

schedules, e.g., tightness of a job with respect to its

due date, an estimated tardiness, and an average slack.

Thus, it is very hard to address the issues of

production scheduling by employing the previous

methods, which cannot deal with feature values of

nonnumeric information in trial schedules. Therefore,

we have to overcome this limitation of the

conventional DNN model to learn a better policy of

allocating operations for manufacturers so that

production schedules contribute towards both

satisfactory factory performance and higher fill rate

constraint.

4 PROPOSED METHOD

To recognize both numeric and nonnumeric

information by a DNN, we propose a new DNN

model. Our approach is based on two concepts: 1) a

schedule can be represented as a graph structure, 2) a

feature value of each node on the graph can be

extracted by GCN. In the graph structure of a

schedule, we can represent numeric information as

attribute values on nodes, and nonnumeric

information as edges. In the GCNN, we can extract

feature values on nodes from its adjacent relations

defined by edges through graph convolutional

operations. Therefore, we can extract feature values

of nodes with respect to both numeric and

nonnumeric information.

In section 4.1 and 4.2, we elaborate on the two

basic concepts, respectively. In section 4.3, we add an

enhancement that reduces the computational time of

the proposed DNN. In section 4.4, we explain how to

make a schedule by using the proposed DNN.

4.1 Schedule Graph

A graph structure is a data structure that consists of

sets of nodes and edges. The relation of two nodes can

be represented by an edge in a graph structure.

In a schedule graph, a node is used to represent a

component of a schedule as shown in Table 1. A

“block” column is used in section 4.3. We divide the

node type of operation into “allocated operation” and

“unallocated operation” so that a DNN can recognize

the difference between the two.

Numeric information is represented as attribute

values on nodes, e.g., an ability on rsc, processing

time on prc, and working period on a/uopr. An ability

attribute on the resource node is used to represent a

difference among resources with the same function.

For unallocated operations, we use the earliest start

and end time that can be allocated because we cannot

use a determined value.

Nonnumeric information is represented as

directed edges, as shown in Table 2, e.g., process

sequence (process) is from/to prc, capable resource of

a process is an edge from prc to rsc, and allocated

resource of an operation is an edge from aopr to rsc.

There are redundant edges as well: process

sequence edge (operation) and capable resource edge

(operation). They are not necessary for defining the

state of a schedule because using a process sequence

edge (process) and a capable resource edge (process)

is sufficient. As such, we use them to improve the

efficiency of a GCN by connecting nodes that are not

connected with a minimum element.

We show an example of a schedule graph in

Figure 1. The graph on the right represents the state

of a schedule, which is depicted on the left. Rsc (X,

Y, and Z), prc (A ~ G), aopr (1, 2, 4, and 6), and uopr

(3, 5 and 7) are defined as nodes. For simplicity, we

do not show a capable resource edge (operation). For

example, process sequence edge from prc A to prc B

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

768

Table 1: Node types of schedule graph.

Name Short Block Attributes

Resource rsc mst Ability

Process prc mst Processing time

Unallocated

Operation

uopr trn

Start date and time,

End date and time,

Working time

Allocated

Operation

aopr sch

Start date and time,

End date and time,

Working time

Table 2: Directed edge types of schedule graph.

Name Block From To

Process sequence

(Process)

mst prc prc

Capable resource

(Process)

mst prc rsc

Operation process trn/sch u/aopr prc

Process sequence

(Operation)

trn/sch u/aopr u/aopr

Capable resource

(Operation)

trn/sch u/aopr rsc

Operation sequence sch aopr aopr

Allocated resource sch aopr rsc

Figure 1: Example of a schedule graph.

implies that prc A is a front process of prc B and prc

B should be performed after prc A; allocated resource

edge from aopr 1 to rsc X implies that aopr 1 is

allocated to rsc X; and operation sequence edge from

aopr 1 to aopr 6 implies that aopr 6 is to be processed

after aopr 1 in the same resource.

This graph needs to be updated when a new

operation is allocated. For example, we assume that

uopr 3 is to be allocated to rsc Z after aopr 4. At first,

node and edge types related to uopr 3 are changed

from uopr to aopr. Next, the following edges are

added to the graph: an operation sequence edge from

aopr 4 to aopr 3 and an allocated resource edge from

aopr 3 to rsc Z.

4.2 Graph Convolution

A GCNN is a form of DNN architecture that is

developed to work on a graph structure (Gilmer et al.,

2017). We define feature values on the nodes of a

GCNN and update them by integrating them with

their adjacent nodes. Through these processes, the

feature values evolve into distinct values that contain

information of their adjacent relations. We can obtain

feature values of schedule components with both

numeric and nonnumeric information and compute a

policy with respect to them in a GCNN applied to a

schedule graph.

Our GCNN consists of three layers: 1) an input

layer, 2) a convolution layer, and 3) an output layer.

All equations are shown from (1) ~ (10) below.



implies concatenation and ⋅ implies inner product. 

and  imply a number of computations. To recognize

the differences in nodes and edges, we use different

parameters in ,,,,,,GRU,LSTM for each

index ,,,, and in/out types of directed edges. All

parameters are initialized by the Xavier’s method

(Glorot et al., 2010).

1) Input layer



















(1)

2) Convolution layer



,















,







,











,









(2)















,









∈



,



(3)







GRU



















,⋯,







#

,







(4)

3) Output layer













,







,







,









,



,

(5)





,





,







(6)











⋅





(7)





Softmax











,⋯,

#







(8)















∈

(9)







,





LSTM

,







,





,







(10)

In input layer (1), we initialize a feature value 





of node  by an affine transformation from an

attribute value 



. Although the dimensions of the

attribute values differ from each other, the

dimensions of the feature values are unified to .

In a convolution layer, we integrate adjacent

relations to a feature value. This layer consists of two

functions: 2-1) a message function and 2-2) an update

function. In a message function, for node  and its

time

X Y Z

A B C D E F G

1 2 3 4 5 6 7

Production Scheduling based on Deep Reinforcement Learning using Graph Convolutional Neural Network

769

adjacent node  connected by edge type , we compute

a message 

,









from node  to node  through edge

type  in (2) and aggregate the messages that are

categorized in the same edge type  to one message













in (3). Adj



,



denotes a set of adjacent nodes

to node  connected by edge type . In update function

(4), we reflect aggregated messages 











on a

feature value 





of node  using a gated recurrent unit

GRU





(Cho et al., 2014). #edge denotes the number of

edge types that are connected to node .

Nonnumeric information, represented as adjacent

relations, is transformed to computations such that

each node receives messages from its adjacent nodes

only. Moreover, by repeating this layer 



times, the

entire information of the graph is reflected through

feature values because feature values of indirectly

connected nodes are propagated to each node.

We compute a policy in an output layer from

feature values computed in a convolution layer. At first,

we compute a feature value of a candidate of an

allocation  in (5). We use several feature values to

represent a candidate with rich information: uopr  to

be allocated, rsc  where uopr  is to be allocated, aopr

 and  that are processed before/after uopr .

Next, we compute a policy from a set of feature

values of candidates by Set2Set architecture (Vinyals

et al., 2015) in (6)-(10). Set2Set architecture is

designed to work on a set of vectors and computes a

feature value of the set itself. We compute a weight 





for each candidate  of the set in (7) and (8) and

summarize them in (9) as a feature value 



of the set.

#cnd and Cnd denotes a number and a set of

candidates, respectively. A feature value





is used to

update hidden values 





,





of candidate  by a long

short-term memory LSTM

,



(Hochreiter et al., 1997)

in (10). By repeating (7)-(10) 



times, complete

information of all candidates are reflected on feature

value 



and weight 



. In this paper, we use the

weight 



as a policy.

As mentioned above, by using integrated feature

values of both complete and detailed information, we

can compute a policy with respect to the requirements

of both managers and shop floors.

4.3 Speed-up of GCNN Computation

In the original concept of a GCNN in section 4.2, we

re-make the feature values of all the nodes and

convolute them using all the edges every time when

selecting an allocation. However, there are minute

changes between a schedule graph and its updated

version, e.g., an operation sequence edge from aopr 4

to aopr 3 and an allocated resource edge from aopr 3 to

rsc Z in the example in section 4.1. Assuming that there

are few differences in the feature values of nodes with

no change, almost all nodes have only a few

differences in their feature values.

Therefore, to reduce computational time, we re-use

feature values computed in previous scheduling steps

and update them for nodes with changes only: dopr 2,

3, 4, prc C, and rsc Z in the example of section 4.1. We

call this partial convolution. To construct a partial

convolution, we reference a GCNN that can deal with

a dynamic change in graph structure (Manessi et al.,

2020; Ma et al., 2018).

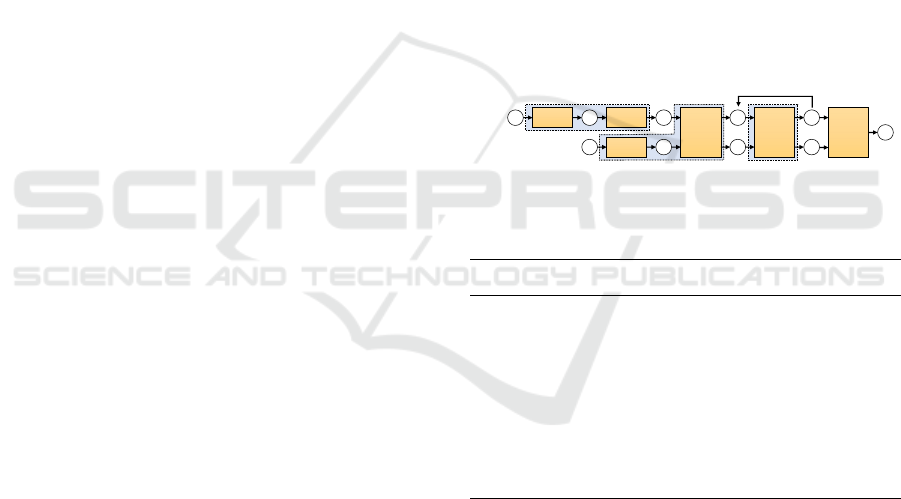
An overview of a GCNN with partial convolution

is shown in Figure 2. We prepare three blocks of

GCNNs: 1) a master block, 2) a transaction block, and

3) a scheduling block, by combining layers of the

original GCN. A scheduling block has a main function

that updates feature values on nodes with changes only

and is executed every time when selecting an allocation.

We use the master and transaction blocks to extract

feature values before we start scheduling.

Figure 2: Overview of graph convolutional neural networks

with partially convolution.

Algorithm 2: Scheduling with partial convolution.

1. execute master block

2. execute transaction block

3. initialize schedule

4. while schedule is not completed:

5. compute a policy by output layer

6. select an allocation by EG or top-k

7. update the schedule

8. execute scheduling block

9. return schedule

We show a procedure of scheduling with partial

convolution in Algorithm 2. At first, we initialize

feature values of nodes categorized to a master block

by an input layer and convolute 





times with nodes

and edges categorized under a master block by a

convolution layer. Then, we initialize feature values on

nodes categorized under transaction block by an input

layer and convolute 





times with nodes and edges

categorized under both master and transaction blocks.

Thereafter, we can start scheduling. When we select an

allocation, we compute a policy by an output layer with

the feature values at that time. After an operation is

mst

trn/sch

 input conv 

 input

conv



output conv



1) master block

2) transaction bloc

3) scheduling block

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

770

allocated, we update feature values of nodes with the

changes by a scheduling block 





times.

4.4 How to Make a Schedule with DNN

Our DNN acquired a rich representation power and it

can memorize a lot of supervised allocations.

However, it is hard for the DNN to memorize all of

them. There are always some mistakes in allocations

in scheduling with a DNN.

Moreover, we make a schedule by successively

selecting allocations and do not change a previously

decided allocation. Therefore, there is some

possibility that mistakes at the opening step of

scheduling leads to the creation of a bad schedule.

To overcome these mistakes made by the DNN,

we make 



schedules as candidates and select one

that maximizes the value of a schedule. When we

make candidates of schedules, we use candidates of

allocations in only top-k of the probabilistic values

and randomly select one from among them.

5 EXPERIMENT

We conduct an experiment to evaluate whether the

value of a schedule made by the proposed method for

problems not used in training gets better with the

number of times of training.

We use a benchmark problem swv11 (50 items

and 10 resources) in OR-Library (Beasley, 1990-

2018). The abilities of resources are unified to 1.0. To

create an artificial problem, we pick up 50 items

randomly from the master data by allowing

duplication. Therefore, each problem has 500

operations.

We evaluate a completed schedule by a makespan

that is related to shortening LT from the perspective

of managers and a degree of satisfaction of basic

constraints of JSP from the perspective of shop floors.

A makespan is a time span from start time to end time

in which all operations are performed. In this paper,

to simplify the problem, we assume that all candidates

of allocations satisfy the basic constraints.

We compare the proposed method (conv.) with

the one without convolution (no conv.). The

comparison uses only numeric information (attribute

values) and leaves out nonnumeric information

(adjacent relations). This enables us to evaluate

whether we need to use nonnumeric information to

construct a good dispatching rule. Moreover, we use

a dispatching method that is used for large-scale

problems. A dispatching rule is the earliest start time

rule as this rule makes the best schedule in a

preliminary experiment.

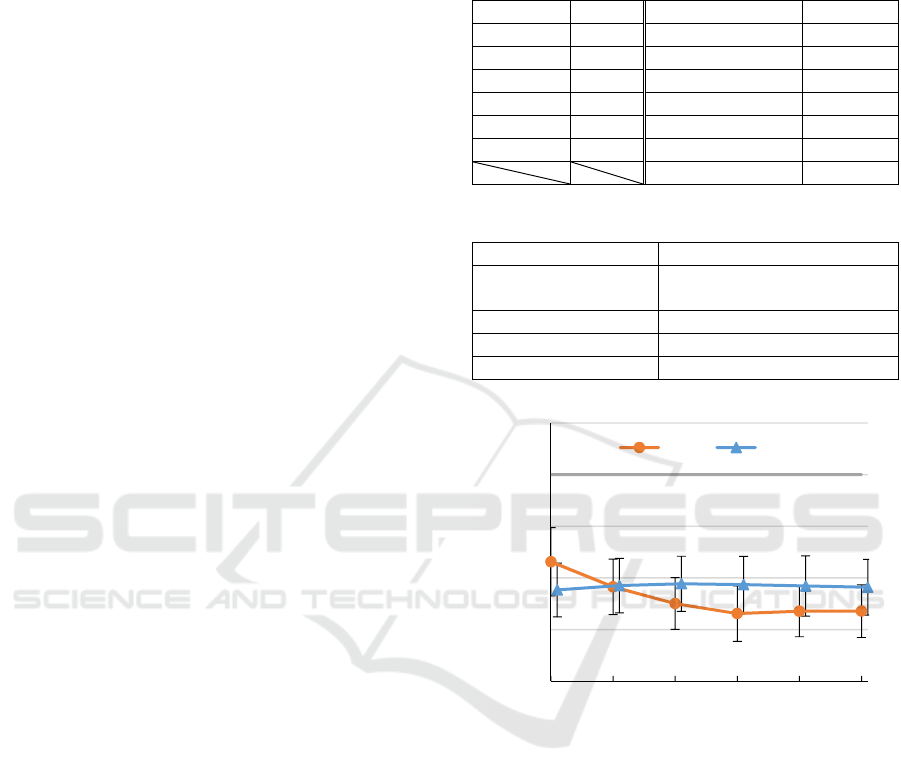
Table 3: Setups of hyper parameters.







128









128









16 / 0





128







16 / 0





128







1 / 0





1.0







Δ

0.1



top-k 2 Epoch 500

Mini-batch 4,000

Table 4: Experimental conditions.

OS Windows 10 Pro

CPU

Intel Core i7-6700HQ,

2.60 GHz

Memory size 16.0 GB

Core number 8

DNN framework PyTorch (1.0.1)

Figure 3: Result of experiment.

The procedure of the experiment is as follows.

First, we prepare 



test problems. Next, we train a

DNN with the algorithm 1 with the training problems.

After step 6, we make a schedule for each test

problem using the method in section 4.4 and evaluate

their makespan. The setups of hyper parameters and

experimental conditions are shown in Table 3 and

Table 4, respectively.

6 RESULT

The results of the experiment are depicted in Figure 3.

We use the ratio of makespan to dispatching method as

0.8

0.85

0.9

0.95

1.05

012345

Ratio to dispatching method

Training number of time

conv. no conv.

Production Scheduling based on Deep Reinforcement Learning using Graph Convolutional Neural Network

771

each problem has a different makespan. The mean

values and standard deviations of 



schedules are

presented in the figure 3. It takes about five weeks for

complete training and about 100 seconds to make 



candidates of schedules.

The values derived by the proposed method

with/without convolution are better than a dispatching

method, even without training (number of times of

training is 0). Thus, it is likely that they find a good

schedule by making a lot of candidates, which is not an

effect of convolutions.

A result worth noting is that a value given by the

proposed method with convolutions improves with the

number of times of training and outperforms the one

without convolutions, which do not give the same

results. With number of times of training at 



, we

achieve an 87 %, 95 %, or 97 % reduction in makespan

as compared to a dispatching method, where number

of times of training is 0, and the proposed method

without convolution. These differences are significant

as per the t-test, which gives   0.05. Therefore, we

consider that the proposed method can select an

appropriate allocation for each state of schedule-

making because the DNN can recognize the state of

making the schedule in detail as a result of

convolutions.

7 CONCLUSION

We study the DRL method for learning dispatching

rules automatically. Our contribution to the existing

literature is a new DNN model that can recognize both

numeric and nonnumeric information of schedule-

making by applying graph structure of a schedule and

a GCNN. Moreover, we reduce computational time of

the GCNN by applying a partial convolution. After

training a DNN using the DRL algorithm, we observed

that the value of a schedule made by the proposed

method for problems not used in training improves

with the number of times of training. Therefore, we can

automatically construct a good dispatching rule and

expect to reduce the work load for scheduling staff.

However, this paper shows that the proposed

method works on a restricted setting only. To use this

method in a practical scenario, additional experiments

and enhancements need to be conducted. First, the

proposed method should work on problems with a

scale of 1,000 operations. Second, the proposed

method should make a schedule subject to individual

constraints.

ACKNOWLEDGEMENTS

We would like to thank Editage (www.editage.com)

for English language editing.

REFERENCES

Beasley, J. E. (1990-2018). Job shop scheduling problem

swv11 (Online), OR-Library, November 7, 2019,

http://people.brunel.ac.uk/~mastjjb/jeb/info.html

Cho, K., Van Merriënboer, B., Gulcehre, C., Bahdanau, D.,

Bougares, F., Schwenk, H., & Bengio, Y. (2014).

Learning phrase representations using RNN encoder-

decoder for statistical machine translation. arXiv

preprint. arXiv:1406.1078.

Gabel, T., & Riedmiller, M. (2008). Adaptive reactive job-

shop scheduling with reinforcement learning agents.

International Journal of Information Technology and

Intelligent Computing, 24.

Gilmer, J., Schoenholz, S. S., Riley, P. F., Vinyals, O., &

Dahl, G. E. (2017). Neural message passing for quantum

chemistry. Proceedings of the 34th International

Conference on Machine Learning, (Vol. 70) (pp. 1263–

1272).

Glorot, X., & Bengio, Y. (2010). Understanding the difficulty

of training deep feedforward neural networks.

Proceedings of the 13th International Conference on

Artificial Intelligence and Statistics (pp. 249–256).

Hochreiter, S., & Schmidhuber, J. (1997). Long short-term

memory. Neural Computation, 9, 1735–1780.

Kingma, D. P., & Ba, J. (2014). Adam: A method for

stochastic optimization. arXiv preprint. arXiv:1412.

6980.

Ma, Y., Guo, Z., Ren, Z., Zhao, E., Tang, J., & Yin, D. (2018).

Streaming graph neural networks. arXiv preprint

arXiv:1810.10627.

Manessi, F, Rozza, A., & Manzo, M. (2020). Dynamic graph

convolutional networks. Pattern Recognition, 97,

107000.

Pinedo, M. L. (2012). Scheduling: Theory, Algorithms, and

Systems (4th ed.). New York: Springer.

Riedmiller, S., & Riedmiller, M. (1999). A neural

reinforcement learning approach to learn local

dispatching policies in production scheduling.

Proceedings of the 16th International Joint Conference

on Artificial Intelligence (Vol. 2) (pp. 764–469).

Vinyals, O., Bengio, S., & Kudlur, M. (2015). Order matters:

Sequence to sequence for sets. arXiv preprint.

arXiv:1511.06391.

Zhang, W., & Dietterich, T. G. (1995). A reinforcement

learning approach to job-shop scheduling. International

Joint Conferences on Artificial Intelligence (Vol. 95) (pp.

1114–1120).

ICAART 2020 - 12th International Conference on Agents and Artiﬁcial Intelligence

772