Self Learning Strategy for the Team Orienteering Problem (SLS-TOP)

A. Goullieux, M. Hiﬁ and S. Sadeghsa

EPROADEA 4669, Universit de Picardie Jules Verne, Amiens, France

Keywords:

Team Orienteering Problem, Local Search, Population, Deep searching, Diversiﬁcation, Self Learning,

Jumping.

Abstract:

The Team Orienteering Problem (TOP) can be viewed as a combination of both vehicle routing and knapsack

problems, where its goal is to maximize the total gained proﬁt from the visited customers (without imposing

the visit of all customers). In this paper, a self learning strategy is considered in order to tackle the TOP,

where information provided from local optima are used to create new solutions with higher quality. Efﬁcient

deep searching (intensiﬁcation) and jumping strategy (diversiﬁcation) are combined. A number of instances,

extracted from the literature, are tested with the proposed method. As shown in the experimental part, one

of the main achievement of the method is its ability to match all best bounds published in the literature by

using a considerably smaller CPU/time. Then, for the ﬁrst preliminary study using both jumping self learning

strategies, encouraging results have been obtained. We hope that a hybridation with a black-box solver, like

Cplex or Gurobi, can be considered as the main future of the method for ﬁnding new bounds, especially for

large-scale instances.

1 INTRODUCTION

Team Orienteering Problem (TOP) belongs to the

combinatorial optimization problems. Where it is

considered as a particular case of the Vehicle Rout-

ing Problem (VRP). In other words, such a prob-

lem is a combination of Knapsack Problem (KP) and

VRP(Bederina and Hiﬁ, 2017). On the one hand, the

goal of the ﬁrst subproblem is to select the customers

by maximizing the total proﬁt. On the other hand,

the second subproblem is related to searching the best

route through the selected customers by minimizing

the total travel time. Each instance of TOP consists

of a limited number of customers, number of vehicles

and an associated maximum time for each tour/travel.

Each customer has an array of three elements; two el-

ements for their corresponding coordination (x and y)

and one for their proﬁt. A tour is a path that starts by

starting depot and ends to ending depot. A feasible

solution is a solution that (i) uses not more than the

maximum number of available vehicles, (ii) each ve-

hicle respects the maximum travel time limit and, (iii)

each customer is visited at most one time. Thus, a so-

lution must select the customers in the route to gain

the maximum proﬁt while some customers cannot be

visited.

Given that the study of VRP and its variants are

NP-hard, thus it cannot be solved optimally in polyno-

mial time (Golden et al., 1987)(Lawler et al., 1985).

Herein, we propose a population-based approach to

handle the problem mentioned above, i.e., TOP. The

proposed approach starts by creating a population

where speciﬁc iterative structures are used. Indeed,

the structures tries to discover the solution space by

applying both deep searching and jumping strategies.

The deep searching applies a variety of neighbor oper-

ators in order to converge towards local optima. Next,

in order to overcome local optima, some diversiﬁca-

tion operators are applied based on jumping principle.

In overall, the algorithm starts with an initial

population containing feasible solutions. Then deep

searching strategy is considered for each created fea-

sible solution. Indeed, it ﬁrst minimizes the time of

the solution thanks to some neighbor operators then it

will maximize its proﬁt by trying to add nodes in pos-

sible positions. Finally, it produces a solution called

saturated solution. A saturated solution is deﬁned as

the one that cannot be improved when deep search-

ing is applied on it; that is, a local optima. Note that

in a saturated solution: (i) All available vehicles are

used, (ii) It is not possible to add nodes from unvisited

customers to the current solution because vehicles are

ﬁnished their maximum time limit.

During the jumping strategy, each saturated so-

lution is subjected to a local destroying procedure

which drops some visited customers. Hence, they

336

Goullieux, A., Hiﬁ, M. and Sadeghsa, S.

Self Learning Strategy for the Team Orienteering Problem (SLS-TOP).

DOI: 10.5220/0008985703360343

In Proceedings of the 9th International Conference on Operations Research and Enterprise Systems (ICORES 2020), pages 336-343

ISBN: 978-989-758-396-4; ISSN: 2184-4372

will be reestablished by calling an enhancing proce-

dure that is able to achieve a new diversiﬁed solu-

tion. The jumping process around a solution, using

destroying and rebuilding, can be viewed as a diver-

siﬁcation strategy. Note also that a saturated solution

is an optimum in the valley (local optimum) but it can

also coincide with a global optimum; both destroying

and rebuilding processes are used to converge the so-

lution towards the global optima. The bounds, related

to solutions achieved at the end of the iterations (the

proposed approach), are compared to the best ones

published in the literature.

To validate the proposed approach, we compared

the achieved results to those extracted from (Chao

et al., 1996)(Tang and Miller-Hooks, 2005)(Archetti

et al., 2007)(Khemakhem et al., 2007)(Ke et al., 2008)

and (Bouly et al., 2010). Note that (Archetti et al.,

2007) and (Ke et al., 2008), represent the results

in multiple executions. Indeed, on the one hand,

(Archetti et al., 2007) proposed a solution based on

two different methods: Tabu Search (TS) and Vari-

able Neighborhood Search (VNS). They reported the

difference between best and worst proﬁts obtained

from three executions used. On the other hand,

(Ke et al., 2008) proposed Ant Colony Optimiza-

tion (ACO) method to solve the TOP. They reported

the average of the proﬁts obtained in multiple execu-

tions. Herein, the achieved bounds, considered as the

ﬁrst preliminary study using destroying and rebuild-

ing strategies, are given in a single execution as like

as the other reported in (Chao et al., 1996) and (Tang

and Miller-Hooks, 2005).

The remainder of the paper is organized as fol-

lows. First, Section 2 exposes the literature review re-

lated to the TOP with some variants. Second, Section

3 describes a formal model of the problem studied.

Third, the proposed solution approach is presented in

Section 4. Fourth, Section 5 evaluates the behavior of

the proposed solution method through a set of bench-

mark instances taken from the literature. Finally, the

last section concludes the study and dresses some per-

spectives.

2 LITERATURE REVIEW

The Orienteering Problem (OP) was ﬁrst introduced

by (Chao et al., 1996), where they described a vari-

ety of Traveling Salesman Problem (TSP) in which a

vehicle will start its trajectory from a starting point

called ”depot”. The vehicle should visit subset of

points in order to maximize the proﬁt that gains from

each visited point. In OP, due to the time or capacity

constraints, the vehicle may not be able to visit all the

points; thus the solution method must wisely choose

the subset of points to visit. The vehicle also must

back to the starting point (or the ending depot) at the

end of its trajectory. Furthermore, the location of each

customer is ﬁxed and each customer must be served

not more than once (for more details, the reader can

be referred to (Chao et al., 1996) and (Lawler et al.,

1985). If we consider OP with multiple vehicles, TSP

will turns into a VRP, then by adapting the feature

of choosing points, OP will be replaced with TOP. In

other words, TOP can be viewed as a generalized ver-

sion of OP with multiple vehicles where in OP the

problem will deal with only one group (Archetti et al.,

2014).

It is worthy to mention, the survey of OP by

(Vansteenwegen et al., 2011) and its extension in

(Gunawan et al., 2016). The work of (Gunawan

et al., 2016) is a comprehensive survey of new vari-

ants of OP, where they also mentioned applications

of OP and recent Benchmark instances which is

after used by many related works such as (Dang

et al., 2011), (Cheong et al., 2006) and (Bouly et al.,

2010). Herein, the used instances, are perused in

(Bouly et al., 2010),(Dang et al., 2011),(El-Hajj et al.,

2016),(Bianchessi et al., 2018) and more (To compare

the results, the interested reader can ﬁnd the other ref-

erences used the same dataset, in the body of this pa-

per).

Please note that, if we redeﬁne this problem where

the number of vehicles are variable, then it is not difﬁ-

cult to proof that there is a conﬂict between the mini-

mum number of vehicles and the maximization of the

total proﬁt. In Multi Objective Combinatorial Opti-

mization (MOCO), the number of efﬁcient solutions

is expected to increase exponentially; in many studies

of MOCO they used approximation solutions rather

than exact ones. Herein, the TOP is tackled as a sin-

gle objective function optimization problem, where

the study can be viewed as a ﬁrst step for studying

the multi-objective optimization problem, like (Bed-

erina and Hiﬁ, 2017). The study of (Ehrgott and

Gandibleux, 2000) can be viewed as a straightforward

of MOCO, where a comprehensive survey on it and

a discussion on their available solution methodolo-

gies are given. They also mentioned complexity of

TOP and the fact that TOP is NP hard. (Keshtkaran

et al., 2016) proposed a branch and price approach

for TOP they also compared their results with other

studies used exact methods for TOP (see (Boussier

et al., 2007)). To refer the most recent article, (Pes-

soa et al., 2019) proposed a branch and cut and price

(BCP) solver as a generic exact solver for VRP and

its variant including KP and also TOP.

In approximation methods, (Coello, 2010) counts

Self Learning Strategy for the Team Orienteering Problem (SLS-TOP)

337

more than 320 papers using population-based solu-

tion methods. On 2011,(Dang et al., 2011) made a

huge progress in TOP by presenting a Particle Swarm

Optimization (PSO) based on memetic algorithm for

TOP. The proposed approach creates a new solu-

tion based on the best founded local solution and

the global local solution. The process of creating a

new solution is based on the well known cross over

function in genetic algorithm. The very same au-

thors extended the study on 2013 with an PSO in-

spired algorithm(Dang et al., 2013b). The complete

solutions with small and large instances are avail-

able at the URL: https://www.hds.utc.fr/

∼

moukrim/

dokuwiki/en/top/ (this study also used the same

benchmark instances of TOP). In the mentioned ar-

ticles they not also provided a solution for all the in-

stances, but also they used a new developed instances

with larger dataset. (Ke et al., 2016), with a study

on 2016, also mentioned that the best founded so-

lution approach in the literature for most of the in-

stances are the ones presented in (Dang et al., 2011)

and (Dang et al., 2013b), both are inspired by the

PSO. Although their proposed algorithm uses an op-

erator called mimic operator to create a new solution

by imitating the old solutions. They also compared

their results with larger instances.

This study propose a self learning strategy in order

to create a solutions with higher quality. It proposed

an operator to imitate the solutions founded from lo-

cal optima to create new solutions.

3 PROBLEM DESCRIPTION

VRP is often represented as a directed graph, where

nodes and edges characterize the customers and

routes, respectively. Let deﬁne S = (N, R) as a fea-

sible solution, where N represents the set of unvis-

ited nodes and R = {r

, r

, .., r

} the set of feasible

routes, where m denotes a maximum number of vehi-

cles. A route r is deﬁned as a permutation of visited

nodes. Each route starts from a node, called ”the start-

ing depot”, visits a subset of customers in a route and,

ﬁnally returns to the ending depot. For each route

the goal is to gain beneﬁts from the visited customers

within a given maximum travel time. All vehicles are

assumed identical and the number of vehicles is ﬁxed

in each dataset. The total time of each route is com-

puted by summation of travel time between the visited

nodes in the route.

Let t

i j

be the travel time between each two visited

nodes (namely i and j, where i 6= j). The total travel

time of the route r

will be calculated as

∑

i, j

i j

where

i, j are visited by vehicle k. In the given dataset the

velocity is assumed as ﬁxed and unique; thus the time

and distance are equal.

The objective function is to maximize the gained

proﬁt from the customers using a ﬁxed number of ve-

hicles and ﬁxed maximum travel time for each route.

In each feasible route

∑

i, j

i j

≤ T

max

, where T

max

de-

notes the maximum travel time of the stated route.

It should be noted that during the one solution time,

each customer must be served fully and in one time

and thus only one vehicle can take proﬁt from it.

Input data associates three numbers x, y and p to

the customers, where x and y indicate the customer

coordination and, p denotes the proﬁt that a vehicle

can gain if visits the delineated customer. Due to

the two constrains, maximum time and limited ve-

hicles, TOP will choose whether to visit a customer

or not. Herein, we assigned a ratio of attractiveness

to the customers. Such a ratio is deﬁned as gained

proﬁt divided by added distance if the vehicle visits

the given customer. It means that customers achiev-

ing greatest ratios of attractiveness have the priority to

be served by the vehicles. Consequently, by choosing

whether to visit the customers, the approach will act

more wisely. Hence, the problem is no longer follows

the typical VRP rule, which is to visit all the clients.

Due to the complexity of the problem (its NP-

hardness), we propose a population-based approach

with a self learning strategy, where a new idea is com-

bined with destroying and rebuilding strategy with a

local search.

4 SOLUTION APPROACH

The proposed approach uses a self learning strategy

in order to create a solutions with higher quality. In

the self learning strategy data from the past is saved

and it is used to create a new solutions. As we dis-

cussed, TOP is a multi layer combinatorial optimiza-

tion problem. It is very important to choose wisely

used parameters and methods (specially local search)

to avoid lifetime calculations. The main motivation

of the self learning strategy came with a theory that

the solution with relatively good qualities following a

similar pattern(s). With digging the literature it is also

said that a provided solutions with PSO has found an

interesting achievement in the quality of the solutions

(Dang et al., 2011). As we know, PSO ﬁnds its way

using the self best local, best local and global best lo-

cal (Dang et al., 2011)(Ke et al., 2016).

The proposed Strategy (by taking into account the

main assumptions of the PSO) uses the best founded

movement for each step of the local search (self-best),

and uses the best local optima (best-local) and the

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

338

global best founded solution (global best) as a pat-

tern to create new solutions. In this way at each iter-

ation, data from the past affects the current decision.

The process is also includes building, breaking (de-

stroying) and rebuilding a series of feasible solutions

to seek the search space with high diversiﬁcation and

deep local search strategies.

The algorithm starts with an initial population and

a ﬁtness function. Initial solutions are created using

the proposed initialization approach. It must be men-

tioned that only feasible solutions are accepted. The

value assigned to each solution is also calculated us-

ing the summation of all the proﬁts gain from the vis-

ited customers. Quality of a solution is related to the

summation of the rout time and gained proﬁt from all

the used vehicles. In other words the best founded so-

lution is a solution that has higher proﬁt in a less tour

time. The process starts with one feasible solution: (i)

local search operators are used in two corresponding

steps for minimizing the travelled time and (ii) maxi-

mizing the proﬁt by adding nodes from unvisited ones

and, (iii) a diversiﬁcation procedure using a perturba-

tion strategy is applied to the current solution. There

is a rule applied in all the three mentioned process:

save the best solution.

Of course, in order to maintain certain degree of

diversify of the solutions in the population, different

strategies to create a starting population are consid-

ered (such as choosing a node randomly in Algo. 2

). It should be mentioned that the number of the solu-

tions for each iteration is ﬁxed to the number of cus-

tomers. To maintain the number of population, only

the solutions with higher qualities is used for the next

iteration. In case of not improving after a number of

iterations, a deep diversiﬁcation is applied by remov-

ing the 60 percent of the visited nodes and creating a

new solution. The algorithm stops with the stop con-

dition which is maximum number of iterations or the

calculation time. The main procedure of SLS-TOP is

given in Algo. 1

The following (sub)sections illustrate the structure

of a solution and the main steps of the proposed ap-

proach.

4.1 Solution Representation

A solution consists of some tours (routes) that each

of them starts from the starting point and ends to the

ending point. It must be mentioned, based on the liter-

ature the start and end point can be exactly the same;

however in this study, we used the benchmark data

sets where the start and end points do not have ex-

actly the same coordination. Depots are distinguish-

able with their zero proﬁt in the database.

Algorithm 1: Self Learning Strategy-based algorithm.

1. Input: A n instance of the TOP

2. Output: The best founded feasible solution

3. Create Population of initial solution (PI)

4. Deﬁne S(b) as a Solution with maximum objec-

tive value

5. Repeat

6. set P:= the size of PI

7. set C:= φ

8. For i=1 to P do

9. S := Imitator(S(b) and the ith solution of the PI )/*

see Imitator operator

10. S := Local Search(S)

11. S:= Jumping Strategy(S)

12. set C := {S}UC

13. Replace the best achieved solution by S(b) if V(S)

¿ V(S(b))

14. End For

15. PI → C UPI

16. Update PI

17. Until The stop condition is reached

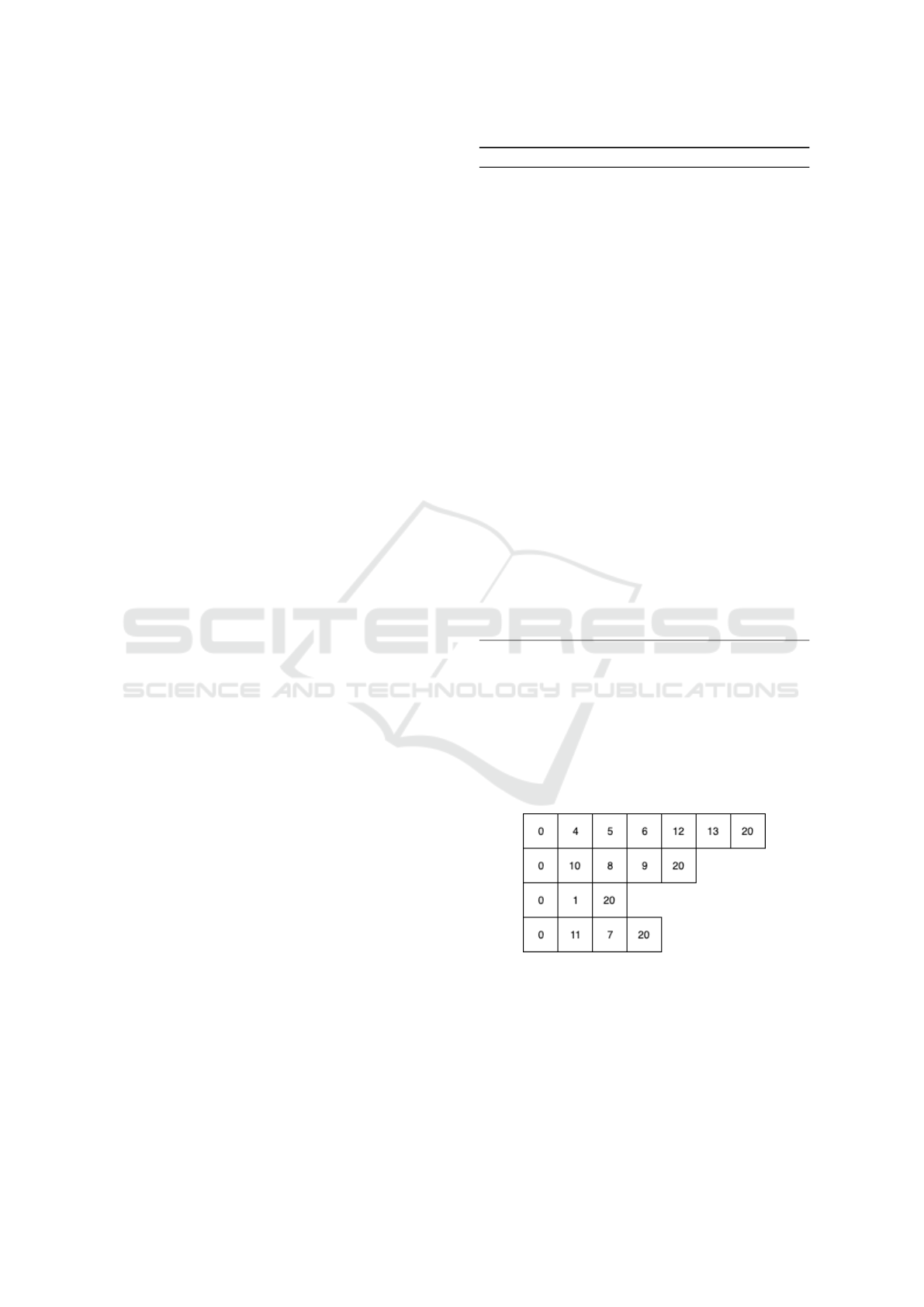
Figure 1 illustration of the solutions structure of

instance P2-04-k of (Chao et al., 1996). it is charac-

terized by 22 nodes including 2 depots and 4 vehicles.

For the best achieved conﬁguration, the total used dis-

tance is equal to 43.044, the best proﬁt is equal to

180, there are 12 visited customers and 8 unvisited

customers.

Figure 1: Best assignment / permutation of the instance P2-

04-k .

4.2 Initial Population

Algorithm 2 describes main steps to create an initial

population; that is, the ﬁrst set of solutions represent-

ing the starting population. Later, the deep searching

strategy is applied for each created solution. In order

Self Learning Strategy for the Team Orienteering Problem (SLS-TOP)

339

to create the initial solutions, we assigned a prefer-

ence ratio to each customer. by taking into account

that each vehicle must start from the starting depot,

the preference ratio for the customers are deﬁned as

the ratio of proﬁt per distance from the starting depot.

The algorithm assignes one customer to each vehicle

at the time (in a parallel way). It means that vehicles

are allowed to visite only one client based on its pref-

erence ratio. Such a method of initialization tries to

create a balanced solution. As a result in a complete

solution, the number of visited customers for all vehi-

cles will be approximately equal (balanced).

4.3 Local Search

Performance of an algorithm is based on the intensiﬁ-

cation of the obtained solution with an astute diversi-

ﬁcation procedure. Herein, the proposed local search

uses deep searching strategy to reﬁne the quality of

the solution at hand. Local search will converge to

the solution toward the local optima. As a matter of

fact local search is a complementary procedure for the

evolutionary process. Local search is consists of two

main steps with the aim of (i) minimizing the travel

time (ii) maximizing the gained proﬁt. Herein, we ap-

ply efﬁcient neighborhood operators in order to inten-

sify the search process. It should be pointed out that

local search will apply for only feasible solutions and

will accept only feasible moves. Local moves in the

intensiﬁcation strategy are described in what follows.

4.3.1 First Step: Time Minimization

This step searches for the permutation of the nodes

with the following operators to minimize the travel

time for each tour: This step includes the permutation

of nodes: (a) in one tour (b) between tours. However

in both cases only the visited node are involved thus

the total proﬁt will remain ﬁxed.

1. 2-opt local search in one tour (exchange two

nodes in a permutation)

2. 3-opt local search in one tour (exchange three

nodes with all the feasible permutations)

3. Remove one node from a tour and insert it in an-

other tour (accept the move if it decrease the sum-

mation of travel times and if it is feasible)

4. Swap a node from a tour with a node from another

tour

Once an operator ﬁnds a better solution, the new

founded solution will be replaced with the initial one

and the algorithm continus to ﬁnd an other better

solution until a stop condition. All operators men-

tioned above are applied for all the visited nodes of

Algorithm 2: Initial population.

1. Deﬁne preference ratio based on ratio of attrac-

tiveness

2. For each vehicle Do

3. Create a list of nodes for the start node based on

the preference ratio (proﬁt / distance from the start

node) in descending order

4. Chose the ﬁrst D nodes. (D is a ﬁxed parameter

that relates to the number of nodes, here we can

assume it is ﬁxed to 10)

5. Create a list of visited nodes and a list of unvisited

ones.

6. Set all customers as unvisited nodes

7. Chose a random node N from the preference list.

8. Assign N to the vehicles one by one according to

the preference list.

9. Update both visited and unvisited lists

10. End For

11. Repeat

12. For each vehicle Do

13. Compute the travel time of the vehicle.

14. Create a list of nodes for the last customer node on

the vehicle based on the preference ratio ( proﬁt

per distance from the start node) in descending or-

der

15. Chose the ﬁrst D nodes. (D is a ﬁxed parameter

that relates to the number of nodes, here we can

assume it is ﬁxed to 10)

16. Chose a random node N from the preference list.

17. If by adding N to the vehicle the travel time + time

to back to depot is less than the maximum travel

time limit

18. Assign N to the vehicle

19. Update both visited and unvisited lists

20. End For

21. Until The stop condition is reached

a given feasible tour. As a result, a new arrangement

of the given feasible tour with minimum travel time is

reached.

4.3.2 Second Step: Proﬁt Maximization

Such an operator will swap or move a node between

tours with the following operators. It aims to ﬁnd the

minimum travel time for the current solution:

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

340

1. Remove a visited node from a tour and insert a not

visited node with a higher ratio of attractiveness.

2. Insert a not visited node in a tour

Both operators are combined with the ﬁrst step in

an iterative manner so that each inserted node will ﬁnd

its best position. As like as the ﬁrst step once an oper-

ator ﬁnds a better solution, the new founded solution

will be replaced with the initial one and the algorithm

continus to ﬁnd an other better solution until a stop-

ping condition.

Local search is applied in an iterative manner.

Once it ﬁnds a feasible solution with less travel time,

it will repeat the searching process from the achieved

solution. The proposed intensiﬁcation strategy will

assure feasibility and improvement of the quality

of the obtained solution. Using the best solution

achieved by the deep searching strategy, an enumera-

tive procedure will try to insert nodes from unvisited

nodes to the solution.

Algorithm 3 describes the process of maximizing

the proﬁt by inserting an unvisited node in a tour.

Note that in case that the local search cannot improve

the initial solution after a number of iterations, the

jumping strategy is applied by removing the sixty per-

cent of the visited nodes and creating a new diversi-

ﬁed solution.

Algorithm 3: Maximizing the proﬁt.

1. Deﬁne S as a feasible solution obtained when us-

ing the deep searching strategy

2. Deﬁne V as a list of visited nodes and N(V ) de-

notes the cardinality of V

3. Repeat for each node {x} belonging to the not

visited nodes:

4. Create S by Adding {x} in a position of S

5. Set N(V ) U {x} → d(S), where d(S) denotes the

travel time of S

6. If S is feasible, i.e., d(S) ≤ T

max

7. Call the deep searching strategy with S

8. Add {x} to the visited list and save S

9. End Repeat

4.4 Jumping Strategy

The jumping strategy tries to diversify the search pro-

cess by building new solutions. It guarantees to con-

verge to an eventual global optima with sufﬁcient it-

erations. Let S be a feasible solution with an objective

value V (S)). The jumping process randomly remove

α(a given percentage) customers from the current so-

lution, providing a partial solution (namely S

with the

rest of the customers. Such a process will perturb the

solution and will move the search space to unvisited

areas. The process of destroying a solution by remov-

ing the customers and building a new solution will

extend the exploration of the search space. Hence,

the strategy can improve the quality of the solution

although there is no guarantee to always improve it.

The stopping criteria for all used procedures are

based upon the number of iterations that comes from

several test experiments. Though to avoid not nec-

essary calculations and save the processor memory,

stopping criterion can be changed with respect to

each step. Limited computational results showed that

for instances extracted from (Chao et al., 1996), the

method is able to match all bounds by using a reason-

able global average runtime.

4.5 Self Learning Strategy

The main part of the approach is the global organiza-

tion of the mentioned methods and the update proce-

dure. As we discussed though the published articles

in the literature, PSO has found interesting (upper)

bounds (especially for large-scale instances). At each

iteration of PSO, it choses its next step by using in-

formation from the best neighbor, the best local and

the global best local. Herein, as already mentioned

(above), the proposed approach mimics such a strat-

egy by considering the best neighbor, the best local

optima and the best achieved solutions as a pattern to

create new solutions. Self Learning Strategy (SLS)

uses an operator called Imitator, so that at each itera-

tion, information taken from the past affects the cur-

rent decision. Such an operator is explained in what

follows.

4.5.1 Imitator Operator

Such an operator combines two solutions and creates

a new solution. It imites parts of two initial solu-

tions by considering two feasible solutions S

and S

which each of them has a maximum m (number of

available vehicles) feasible tours and a list of unvis-

ited customers. Imitator will create a feasible solu-

tion S by imitating a part of S

with S

. Algorithm 4

illustrate the main steps used by the imitator operator.

Imitator creates a new solution by storing in-

formation extracted from an other solution. Such

an operator is used to produce new solutions (short

diversiﬁcation) and also to create a new solution

based on global best and local best solutions at each

iteration.

Self Learning Strategy for the Team Orienteering Problem (SLS-TOP)

341

Algorithm 4: Imitator.

1. Input: feasible solutions S

and S

2. Output: a feasible solution S

3. For all the vehicles:

4. Take tour T

from S

and tour T

from S

5. create a list of nodes L

by ﬁrst half of the visited

nodes in T

6. create a list of nodes L

by second half of the vis-

ited nodes in T

7. Creat T (which can be not feasible) → L

U L

8. remove repeated nodes in T

9. Repeat while T is not feasible

10. remove a node with least proﬁt

11. End Repeat

12. Create a new solution S by replacing T in T

and

save the rest of the solution S

13. S → feasible(S)

14. End For

5 EXPERIMENTAL PART

The proposed method was coded in C++ on OS ver-

sion 10.14.5 with 2.3 GHz Intel Core i5 processor.

The behavior of the proposed approach (noted SLS)

was evaluated on seven sets of instances taken from

(Chao et al., 1996). These sets contain 387 instances

varying from small to large-scale instances. In fact,

these sets are characterized by different maximum

travel times and for each set the number of vehicles

varies from 2 to 4. Coordination and the amount of

proﬁt of the customers are identical for each set. As

noted in (El-Hajj et al., 2016), families with more

available vehicles and higher values of travel time are

more difﬁcult to solve. This is the case for the fam-

ilies 4, 5 and 7. Contrarily, families 1, 2 and 3 are

solved with no difﬁculties (even with exact methods

(Fischetti et al., 1998)(Dang et al., 2013a)), due to

their small number of customers. The other factor that

can effect the difﬁculties to solve is the distribution of

the customers and/or their geometric structure. This

is the case for the families 5 and 6. where customers

with larger proﬁts have more distance to the depots.

Table 1 provides the characteristics of each sets in

the (Chao et al., 1996) benchmark dataset.

A good parameter settings can be achieved

through experimental tests. In local search phase,

some parameters (number of iterations, number of so-

Table 1: Characteristics of instances (Chao et al., 1996).

set n m T

max

Nb of instances

1 32 2, 3,4 2,5 to 21,2 54

2 21 2, 3,4 7,5 to 11,2 33

3 33 2, 3,4 7,5 to 27,5 60

4 100 2, 3,4 25,0 to 60,0 60

5 66 2, 3,4 2,5 to 32,5 78

6 64 2, 3,4 7,5 to 20,0 42

7 102 2, 3,4 10,0 to 100,0 60

lutions/population size) must be such strong to ﬁnd

the local optima and in coefﬁcient of the diversiﬁca-

tion must be high to visit the search space. In gen-

eral, the coefﬁcient of the diversify must not exceed

30% of the total number of customers. The achieved

bounds are also compared to those available in the lit-

erature (extracted from (Bouly et al., 2010)). Herein,

due to the limited space, we only presented sample of

instances in Table2 compared with those published in

the literature.

Table 2: Comparative results.

Instance ACO VNS MA SLS Best

P1 04 r 210 210 210 210 210

P1 02 d 30 30 30 30 30

P1 03 q 230 230 230 230 230

P2 03 k 200 200 200 200 200

P2 04 e 70 70 70 70 70

P2 04 k 180 180 180 180 180

P3 03 i 330 330 330 330 330

P3 04 t 670 670 670 670 670

P5 2 Z 1672.5 1670 1680 1680 1680

P5 4 z 1585.5 1620 1620 1620 1620

ACO, VNS and MA in column header of Table

2 are refers to the solution methods provided by (Ke

et al., 2008), (Archetti et al., 2007) and (Bouly et al.,

2010) respectively. From Table2 , one can observe

that for all considered instances, the proposed method

is able to match all better bounds extracted from the

literature. In fact, for these instances, the proposed

method matches all better bounds reached by MA al-

gorithm, it improves one bound when compared to

those provided by VNS approach and, in two cases

it dominates those achieved by ACO method.

6 CONCLUSIONS

The team orienteering problem can be viewed as a

combination of both vehicle routing and knapsack

problems. The goal of the problem is to maximize the

total proﬁt related to the visited customers. Herein, a

self learning strategy was proposed for approximately

solving the problem. Such an approach is based upon

ICORES 2020 - 9th International Conference on Operations Research and Enterprise Systems

342

a population-based approach, where deep searching

and jumping strategies cooperate. The proposed pre-

liminary computational results showed that the pro-

posed approach remains competitive by matching all

the better bounds extracted from several papers of the

literature. Finally, as a future work we ﬁrst plan to

hybridize the speciﬁc jumping strategy with variable

ﬁxation strategy: in this case, some favorite costumers

can be automatically ﬁxed to the optimum and the re-

duced problem can be solved by calling the method

presented in this study. Second and last, we plan to

inject a black-box solver in order to build a matheuris-

tic for tackling some reduced subproblems that is able

to achieve better bounds, especially for large-scale in

stances.

REFERENCES

Archetti, C., Hertz, A., and Speranza, M. G. (2007). Meta-

heuristics for the team orienteering problem. Journal

of Heuristics, 13(1):49–76.

Archetti, C., Speranza, M. G., and Vigo, D. (2014). Chapter

10: Vehicle routing problems with proﬁts. In Vehicle

Routing: Problems, Methods, and Applications, Sec-

ond Edition, pages 273–297. SIAM.

Bederina, H. and Hiﬁ, M. (2017). A hybrid multi-objective

evolutionary algorithm for the team orienteering prob-

lem. In 2017 4th International Conference on Con-

trol, Decision and Information Technologies (CoDIT),

pages 0898–0903. IEEE.

Bianchessi, N., Mansini, R., and Speranza, M. G. (2018).

A branch-and-cut algorithm for the team orienteering

problem. International Transactions in Operational

Research, 25(2):627–635.

Bouly, H., Dang, D.-C., and Moukrim, A. (2010). A

memetic algorithm for the team orienteering problem.

4or, 8(1):49–70.

Boussier, S., Feillet, D., and Gendreau, M. (2007). An ex-

act algorithm for team orienteering problems. 4or,

5(3):211–230.

Chao, I.-M., Golden, B. L., and Wasil, E. A. (1996). The

team orienteering problem. European journal of op-

erational research, 88(3):464–474.

Cheong, C. Y., Tan, K. C., Liu, D., and Xu, J.-X. (2006).

A multiobjective evolutionary algorithm for solving

vehicle routing problem with stochastic demand. In

2006 IEEE International Conference on Evolutionary

Computation, pages 1370–1377. IEEE.

Coello, C. A. C. (2010). List of references on evolutionary

multiobjective optimization. URL¡ http://www. lania.

mx/˜ ccoello/EMOO/EMOObib. html.

Dang, D.-C., El-Hajj, R., and Moukrim, A. (2013a). A

branch-and-cut algorithm for solving the team orien-

teering problem. In International Conference on AI

and OR Techniques in Constriant Programming for

Combinatorial Optimization Problems, pages 332–

339. Springer.

Dang, D.-C., Guibadj, R. N., and Moukrim, A. (2011). A

pso-based memetic algorithm for the team orienteer-

ing problem. In European Conference on the Appli-

cations of Evolutionary Computation, pages 471–480.

Springer.

Dang, D.-C., Guibadj, R. N., and Moukrim, A. (2013b).

An effective pso-inspired algorithm for the team ori-

enteering problem. European Journal of Operational

Research, 229(2):332–344.

Ehrgott, M. and Gandibleux, X. (2000). A survey and an-

notated bibliography of multiobjective combinatorial

optimization. OR-Spektrum, 22(4):425–460.

El-Hajj, R., Dang, D.-C., and Moukrim, A. (2016). Solv-

ing the team orienteering problem with cutting planes.

Computers & Operations Research, 74:21–30.

Fischetti, M., Gonzalez, J. J. S., and Toth, P. (1998). Solv-

ing the orienteering problem through branch-and-cut.

INFORMS Journal on Computing, 10(2):133–148.

Golden, B. L., Levy, L., and Vohra, R. (1987). The ori-

enteering problem. Naval Research Logistics (NRL),

34(3):307–318.

Gunawan, A., Lau, H. C., and Vansteenwegen, P. (2016).

Orienteering problem: A survey of recent variants, so-

lution approaches and applications. European Journal

of Operational Research, 255(2):315–332.

Ke, L., Archetti, C., and Feng, Z. (2008). Ants can solve the

team orienteering problem. Computers & Industrial

Engineering, 54(3):648–665.

Ke, L., Zhai, L., Li, J., and Chan, F. T. (2016). Pareto mimic

algorithm: An approach to the team orienteering prob-

lem. Omega, 61:155–166.

Keshtkaran, M., Ziarati, K., Bettinelli, A., and Vigo, D.

(2016). Enhanced exact solution methods for the team

orienteering problem. International Journal of Pro-

duction Research, 54(2):591–601.

Khemakhem, M., Semet, F., and Chabchoub, H. (2007).

Heuristique bas

ee sur la m

emoire adaptative pour le

probl

eme de tourn

ees de v

ehicules s

electives. In SM-

CIEEE, r

edacteur, Proceeding de la conf

erence en Lo-

gistique et Transport LT, volume 7.

Lawler, E. L., Lenstra, J. K., and Kan, A. R. (1985). Db

shmoys. the traveling salesman problem. A Guided

Tour of Combinatorial Optimization,” Wiley.

Pessoa, A., Sadykov, R., Uchoa, E., and Vanderbeck, F.

(2019). A generic exact solver for vehicle routing and

related problems. In International Conference on In-

teger Programming and Combinatorial Optimization,

pages 354–369. Springer.

Tang, H. and Miller-Hooks, E. (2005). A tabu search heuris-

tic for the team orienteering problem. Computers &

Operations Research, 32(6):1379–1407.

Vansteenwegen, P., Souffriau, W., and Van Oudheusden, D.

(2011). The orienteering problem: A survey. Euro-

pean Journal of Operational Research, 209(1):1–10.

Self Learning Strategy for the Team Orienteering Problem (SLS-TOP)

343