
Fast Fourier Transform based Force Histogram Computation for 3D
Raster Data
Jaspinder Kaur, Tyler Laforet and Pascal Matsakis
Department of Computer Science, University of Guelph, Guelph, Canada
Keywords:
Relative Position Descriptor, Computer Vision, Image Processing, Force Histogram.
Abstract:
The force histogram is a quantitative representation of the relative position between two objects. Two practical
algorithms have been previously introduced to compute the force histogram between objects: the line-based
algorithm (which works well with 2D data, but is computationally unstable in the case of 3D data), and the
Fast Fourier Transform (FFT)-based algorithm (which is inefficient in the case of 2D data, but has not been
implemented for 3D data). In this paper, an efficient FFT-based algorithm for force histogram computation
in the case of 3D raster data is introduced. Its computation time is compared against that of the 3D line-
based algorithm; except in a few cases, the computation time for new FFT-based algorithm is less than that of
3D line-based algorithm. The experiments validate that the FFT-based algorithm is computationally efficient
regardless of the number of directions, type of forces, and shape of the objects (convex, concave, disjoint or
overlapping).
1 INTRODUCTION
Humans often rely on the relative positioning of the
objects around them in order to understand and ex-
press spatial information. In our daily lives, the
relative position of objects is often communicated
through linguistic expressions like, “the shopping
mall is south of the apartment”, “the school is near
my home”, and “the folder is inside the case”. Spa-
tial prepositions like “north”, “inside” and “nearby”
represent spatial relationships. Distance relationships
(Ryoo and Aggarwal, 2009) describe how far apart the
objects are in space, like “far away”, “nearby”, “at”.
Directional relationships (also called cardinal or pro-
jective (Gapp, 1995) relationships) are mostly iden-
tified by words like “west”, “to the right of”. Topo-
logical relationships specify concepts of connectivity,
adjacency and enclosure (Egenhofer, 1989; Schneider
and Behr, 2005; Egenhofer, 1990).
Comprehending the spatial relationships in a
scene plays a vital role in several areas such as pat-
tern recognition, human-robot communication, scene
description in natural language, image understanding
and so forth. Models of spatial relationships (dis-
tance, directional and topological) among spatial enti-
ties are either quantitative or qualitative. In qualitative
models (Frank, 1996), a relationship either holds or
does not hold. On the other hand, in quantitative mod-
els, a relationship may hold to some degree (Deselaers
et al., 2004). Over the years, qualitative models have
been used in various areas of computer vision. How-
ever, most practical applications of computer vision
and image processing (Smeulders et al., 2000; Skubic
et al., 2001; Skubic et al., 2002; Miller and Wentz,
2003) require quantitative models called relative po-
sition descriptors (RPD).
Relative position descriptors are vectors of val-
ues that encode information about an object’s position
relative to another object. RPDs bridge the gap be-
tween low-level spatial features (e.g., pixels in an im-
age) and high level concepts (i.e spatial relationships).
An ideal relative position descriptor encapsulates all
possible spatial relationship information between ob-
jects, and allows that information to be extracted effi-
ciently. Over the years, much attention has been paid
towards identifying effective approaches for mod-
elling objects’ relative positions. Several RPDs have
been introduced (Miyajima and Ralescu, 1994; Kr-
ishnapuram et al., 1993; Naeem and Matsakis, 2015).
The force histogram (Matsakis, 1998; Matsakis and
Wendling, 1999) may be one of the most well known
relative position descriptors with various theoretical
and practical applications. It encapsulates the struc-
tural information (e.g., size, shape, etc.) as well as
the spatial relationship information between objects.
So far, many algorithms for force histogram compu-
Kaur, J., Laforet, T. and Matsakis, P.
Fast Fourier Transform based Force Histogram Computation for 3D Raster Data.
DOI: 10.5220/0008985100690074
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 69-74
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
69

tation have been introduced. The two main algorithms
for force histogram computation are the line-based al-
gorithm and the Fast Fourier Transform (FFT)-based
algorithm. The line-based algorithm for force his-
togram computation exists for 2D raster objects, 2D
vector objects, 3D raster objects and 3D vector ob-
jects, although the algorithms for the 3D objects are
computationally costly. On the other hand, the FFT-
based algorithm exists only for 2D raster data, and has
not yet been implemented for 3D raster objects.
This paper presents an extension of the FFT-based
algorithm for the computation of force histogram in
the case of 3D raster objects. In Section 2, we dis-
cuss the force histogram and provide a brief overview
of various algorithms found in the literature for com-
puting the force histogram. In Section 3, the algo-
rithm which involves handling 3D raster objects is
presented. Section 4 presents the experiments and a
comparative study in which the line-based force his-
togram is compared against the FFT-based force his-
togram. Section 5 concludes the discussion and pos-
tulates future work.
2 BACKGROUND
2.1 Force Histogram
A histogram of forces F
AB
t
(θ) is a function from IR
(the set of directions) to IR
+
(the set of real numbers)
that represent the position of object A relative to ob-
ject B (Figure 1b). For a given direction θ, the value
F
AB
t
(θ) is the sum of the magnitude of all elemen-
tary forces exerted by the points of B on those of A;
this in turn tends to move A in the direction θ (Fig-
ure 1a). Here, the object A is called the argument and
the object B is called the referent. The magnitude of
each elementary force is given by 1/|r|
t
, where r is
the distance between points and t is any real number.
The function F
AB
t
(θ) has two special cases: t = 2, and
t = 0. When t = 2, F
AB
2
(θ) is called the gravitational
force histogram, and the forces between the points are
inversely proportional to the the square of distance be-
tween them (1/r
2
). When t = 0, F
AB
0
(θ) is called the
constant force histogram, and the forces do not de-
pend on this distance.
2.2 Algorithms for the Force Histogram
Computation
2.2.1 Line-based Algorithm
Matsakis indicates in (Matsakis, 1998; Matsakis and
Wendling, 1999) that the force histogram between ob-
Figure 1: Force histogram: (a) Consider two objects A and
B; F
AB
t
(θ) is the scalar resultant of elementary forces in the
direction θ. (b) The histogram F
AB
t
between the objects A
and B.
jects in an image can be computed by first partition-
ing the image into a number of raster lines, and then
batch-processing pixels on each line. Consider ob-
jects A and B; for any oriented line Λ, F
AB
t
(θ) is the
scalar resultant of elementary forces exerted by points
of B ∩Λ on those of A ∩Λ in a direction θ. In an
ideal case, the shapes of objects A and B are simple
(e.g., convex). For any direction θ, the line Λ inter-
sects each object exactly once, thus the number of
segments A ∩Λ and B∩Λ included in a line is at most
2. The computation of the force histogram is equiva-
lent to computing forces between two segments, thus
lowering the computation time. In the worst case, ob-
jects A and B have complex shapes (e.g., a fractal-like
structure or objects with multiple disconnected com-
ponents). For any direction θ, the line Λ intersects
each objects multiple times, thus the number of seg-
ments A ∩Λ and B ∩Λ may be very high. This will
lead to computing forces between multiple segments,
thus increasing the computation time.
In (Ni et al., 2004), the line-based algorithm for
force histogram computation is extended for 3D data.
The basic principal remains unchanged. For any di-
rection
~
θ (here defined by a unit vector), the function
F
AB
t
(
~
θ) is the scalar resultant of elementary forces ex-
erted by the voxels of B on those of A. The
~
θ is taken
from a set D
K
of evenly distributed reference direc-
tions (Bourke, 2007). The K reference directions in
the set D
K
should follow three primary constraints:
1. They should be evenly distributed in 3D space,
2. They should include six primitive directions i.e.,
(±1,0,0) (left/right), (0,±1,0) (above/below), and
(0,0,±1) (front/behind), and,
3. If a direction θ belongs to the set, then the op-
posite direction −θ should also be a part of the
direction set.
The above constraints indicate m = 6 + 8l, where
6 denotes six primitive directions, 8 denotes the re-
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
70

gions demarcated by the XY, YZ, ZX plane, and l
implies the number of reference directions in each
plane. 3D data, however, is significantly larger than
2D data, so it is necessary to follow appropriate op-
timization techniques. Therefore, a number of irrele-
vant directions are identified and dropped in order to
ease the computational burden. Forces in the remain-
ing directions are computed in a similar fashion to the
2D case. A simple yet powerful test is conducted to
drop irrelevant directions. According to the test in (Ni
et al., 2004), a direction
~
θ is considered relevant, if
F
AB
t
(
~
θ) 6= 0 i.e., for any oriented line Λ, A∩Λ6= 0 and
B ∩Λ 6= 0. Otherwise, a direction
~
θ is irrelevant, and
should not be considered while computing the force
histogram F
AB
t
(θ).
2.2.2 FFT-based Algorithm
The line-based algorithm that is based on the image
partitioning and batch processing of pixels (Section
2.2.1) has two significant drawbacks: (1) the compu-
tation time is directly proportional to the number of
directions (K) in which the forces are evaluated, and
(2) it depends on the shape of the object (concave
or convex) and their relative position (overlapping
or disjoint). To solve the issues encountered by
the line-based algorithm, Matsakis and Jing Bo Ni
(Ni and Matsakis, 2010) introduced an alternative
definition for force histogram computation. Consider
A and B are the membership functions of objects in
a digital image. The image is extended through zero
padding to occupy the infinite space Z
2
, where Z
denotes the set of all integers. .The force histogram is
derived from the mapping Ψ
AB
defined over discrete
space. The mapping Ψ
AB
from Z
2
to IR is defined as
follows:
Ψ
AB
(d,e) =
Z
+∞
−∞
Z
+∞
−∞
A(x,y)B(x + d,y + e)dx dy
(1)
This is a spatial correlation that provides raw infor-
mation about the relative positions of objects, and
can be computed quickly by using the Fast Fourier
transform (FFT). The force histogram
ˆ
F
AB
t
(θ) can
be computed using the mapping defined in Equation
(1). For two objects A and B, the function
ˆ
F
AB
t
(θ) is
defined by:
ˆ
F
AB
t
(θ) =
Z
∞
0
Ψ
AB
(d
~
θ)
r
t
dr (2)
The FFT-based algorithm has been implemented only
for 2D raster objects; it has not been implemented for
3D raster objects.
3 FFT-BASED ALGORITHM FOR
3D RASTER DATA
In this section, we introduce the first FFT-based algo-
rithm for the computation of force histogram in the
case of 3D raster objects. The basic principle re-
mains the same. A force histogram is computed us-
ing a mapping Ψ
AB
defined over the 3D space, where
Ψ
AB
is the spatial correlation between two 3D objects.
A Fast Fourier Transform (FFT) technique is used to
compute the mapping Ψ
AB
quickly. Section 3.1 fo-
cuses on the implementation of the spatial correlation
(Ψ
AB
), then Section 3.2 discusses the computation of
the force histogram using Ψ
AB
.
3.1 Implementation of Ψ
AB
Consider A and B as two 3D raster objects in a
domain G
h×k×l
. Ψ
AB
provides raw information about
the position of object A relative to object B. The
spatial correlation Ψ
AB
between 3D raster objects A
and B is defined as follows:
Ψ
AB
(d,e, f ) =
h−1
∑
h=0
k−1
∑
k=0
l−1
∑
l=0
A(x,y,z)B(x+d,y+e,z+ f )
(3)
The set G
h×k×l
= {−h + 1........h − 1}×{−k +
1........k − 1}×{−l + 1........l − 1} is the effective
domain of Ψ
AB
. In Equation (3), we suppose
that B(x + d,y + e,z + f ) = 0, if the voxel (x + d,
y + e, z + f ) lies outside of G
h×k×l
; such that
(x + d,y + e,z + f ) /∈ {0 .. . h −1} × {0 ... k −1} ×
{0.. .l −1}. It is not difficult to see that only voxels
(d,e,f) that are in the effective domain G
h×k×l
, will
satisfy Ψ
AB
6= 0. Consider the reflection of object A
about the origin, such that A
0
(−x,−y,−z) = A(x,y,z).
By replacing A(x,y,z) with A
0
(x
0
,y
0
,z
0
) in Equation 3,
where x
0
= −x, y
0
= −y and z
0
= −z, we get,
Ψ
AB
(d,e, f ) =
h−1
∑
h=0
k−1
∑
k=0
l−1
∑
l=0
A(x
0
,y
0
,z
0
)B(d −x, e −y, f −z)
(4)
Equation (4) refers to the 3-D discrete convolution.
Using matrix notation, we get:
[Ψ
AB
] = [A
0
] ⊗[B
0
], (5)
where ⊗ is the convolution operator. According to
the Convolution theorem, the Fourier transform has
the power to convert the convolution operation into
an ordinary multiplication, and vice versa. Using the
Convolution theorem, equation (5) can be written as:
Fast Fourier Transform based Force Histogram Computation for 3D Raster Data
71

[Ψ
AB
] = W
−1
2h−1
·W
−1
2k−1
[(W
2h−1
·W
2k−1
·[A
0
] ·W
2l−1
)
×(W
2h−1
·W
2k−1
·[B
0
] ·W
2l−1
)] ·W
−1
2l−1
(6)
where W
i
and W
−1
i
are the Fourier and inverse Fourier
transform matrices of order i and × is the matrix prod-
uct. From Equation (6), computation of [Ψ
AB
] re-
quires three 3-D discrete Fourier transforms. Using
the Convolution theorem, Ψ
AB
can be computed in
O(NlogN) time as this is the complexity of the Fast
Fourier transform (FFT).
3.2 Implementation of
ˆ
F
AB
t
In this section,
ˆ
F
AB
t
is computed using the spatial
correlation Ψ
AB
(Section 3.1). Only a finite number
of directions θ are considered. A reasonable choice
for θ (Section 2.2.1) is to choose from a set of
evenly distributed reference directions D
K
. For 3-
dimensional objects, Equation (2) takes the following
form:
ˆ
F
AB
t
(θ) =
Z
∞
0
Ψ
AB
(dcosθ,dsinθ,z)
r
t
dr (7)
The FFT-based algorithm described in this paper
runs in O(NlogN) time. The computation time for
the FFT-based algorithm is independent of the type of
forces (t) and number of directions (K) in which the
forces are measured. All objects regardless of their
shape (complex or simple) and relative position (dis-
joint or overlapping) are treated in the same manner.
The experiments conducted in Section 4 validate this.
4 EXPERIMENTS
In this section, F
AB
t
denotes a force histogram com-
puted using the line-based algorithm and
ˆ
F
AB
t
denotes
a force histogram computed using the new FFT-based
algorithm. The experiments are conducted on a va-
riety of 3D raster objects. The test data consists of
objects generated from quadratic Koch island fractals
at iterations 2 and 3, overlapping objects, cubes and
segmented cubes (Figure 2). The size of the objects is
kept constant (N = 512
3
) for all experiments, except
for the scenario where the effect of size is investigated
on the computational time of
ˆ
F
AB
t
and F
AB
t
. The al-
gorithms are implemented in C, and the experiments
were conducted on a mac OS equipped with an 2GHz
Intel Core i5 CPU and 8GB of memory. The compu-
tation time is measured using the C library function
clock().
Table 1: Tversky Index (µ
T
), N = 512
3
, K=1800.
Figure 2 (a) (b) (d)
t= 0 0.91 0.86 0.956
t= 1 0.90 0.82 0.950
t = 2 0.87 0.8 0.943
4.1 Comparing Histogram Values
This experiment demonstrates that F
AB
t
and
ˆ
F
AB
t
are almost identical, as expected. The histogram
associated with the F
AB
t
is denoted as h
1
(θ) and
the histogram associated with
ˆ
F
AB
t
is denoted as
h
2
(θ). The dissimilarity between h
1
(θ) and h
2
(θ) is
measured using the Tversky index (µ
T
):
µ
T
(h
1
,h
2
) =
∑
K−1
i=0
min
{
h
1
(θ
i
),h
2
(θ
i
)
}
∑
K−1
i=0
max
{
h
1
(θ
i
),h
2
(θ
i
)
}
(8)
µ
T
is 1 when the h
1
(θ) and h
2
(θ) histograms are ex-
actly the same and µ
T
is 0 when the h
1
(θ) and h
2
(θ)
histograms are orthogonal. The µ
T
values tend to be
close to 1 for the object pairs considered in our ex-
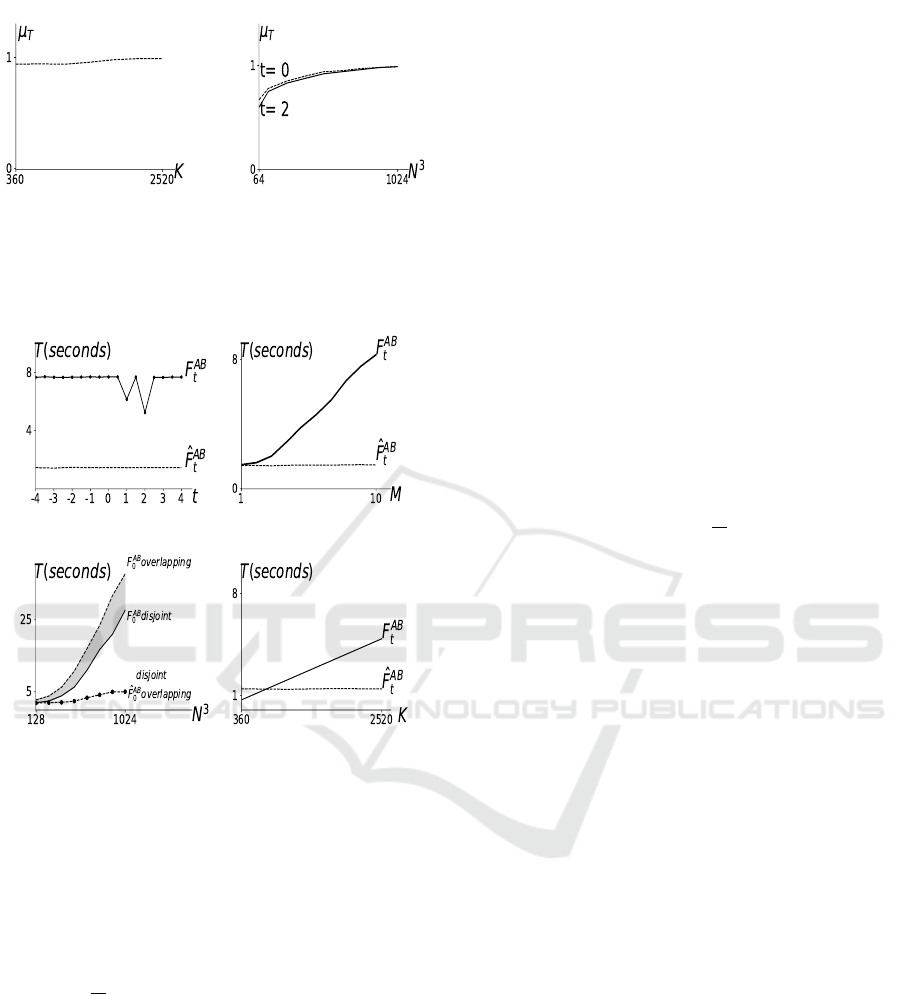
periments (Table 1). The effect of K and N on µ
T
has
also been studied (Figure 3). The values of µ
T
are al-
most independent of K (Figure 3a) but grow notably
and tend towards 1 when N increases (Figure 3b).
4.2 Comparing Computation Time
The results presented in Figure 4a shows that the com-
putation of
ˆ
F
AB
t
is independent of the choice of t;
however, F
AB
t
computes faster when t=1 or t=2. The
prominent reason for this is because the computation
of each F
AB
t
devolves into evaluating a number of nu-
merical expressions which are computationally faster
when t=1 and t=2.
(a) $$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$(b)$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$(c)$
A$
B$
A$
B$
A$
B$
!
!
!
!
!
!
!
!
!
!
!
!
!
!!!!!(d)!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!(e)!
!!A!
A!
!!B!
A!
A!
B!
A!
B!
Figure 2: Test Data: The 3D objects used in this experiment
are right cylinders whose bases are quadratic Koch island
fractals at (a) iteration 2 and (b) iteration 3. Also shown are
(c) overlapping objects, (d) cubes and (e) segmented cubes.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
72
(a) (b)
Figure 3: (a) µ
T
against the number of directions (K), ob-
jects are from Figure 2b and N = 512
3
.(b) µ
T
against the
number of voxels (N), objects are from Figure 2b and K =
1800.
(a) (b)
(c) (d)
Figure 4: In (a), the objects are from Figure 2a, K= 1800,
N = 512
3
. In (b), the objects are from Figure 2e, M denotes
the number of disconnected components in an object, K=
1800, N = 512
3
. In (c), the objects are from Figure 2(b,c),
K= 1800. In (d), the objects are from Figure 2c, N = 512
3
.
In an ideal case, the computational complexity of
F
AB
t
is O(KN) for simple object shapes, whereas for
complex shapes (e.g, objects with multiple discon-
nected parts) the computational complexity of F
AB
t
is O (KN
√
N). The main reason for this is that for
simple convex objects (Figure 2d), any line that runs
through both objects intersects each object only once;
therefore, computing a force histogram value comes
down to computing the forces between two segments.
However, for complex shapes (Figure 2e), any line
passing through both objects intersects them in multi-
ple segments; therefore, computing a histogram value
comes down to computing the forces between a large
number of segments which further leads to longer
processing times (Section 2.2.1). However, the
ˆ
F
AB
t
always computes in O(NlogN) regardless of the ob-
ject’s shape. This is illustrated by Figure 4b. Further-
more, the relative position (disjoint or overlapping) of
the objects also affects the processing time of F
AB
t
,
whereas
ˆ
F
AB
t
stays the same for disjoint as well as
overlapping objects (Figure 4c). Finally, when K in-
creases, the processing time of F
AB
t
also grows lin-
early. On the other hand,
ˆ
F
AB
t
remains constant (Fig-
ure 4d).
5 CONCLUSION
The FFT-based algorithm for the computation of force
histogram is a powerful tool to quantitatively repre-
sent the relative position between two objects. In ear-
lier work, only 2D objects were considered. In this
paper, we have shown that 3D objects can also be
handled, and efficiently. The FFT-based algorithm for
the force histogram computation described in this pa-
per is computed in O(NlogN) time, where N is the
number of voxels in an object. In comparison, the
line-based algorithm for the force histogram compu-
tation is computed in O (KN
√
N) time, where K is the
number of direction in which forces are computed.
Furthermore, contrary to the line-based algorithm, the
computation time of the FFT-based algorithm is inde-
pendent of the number of directions, type of forces,
shape and relative position of the objects. The FFT-
based algorithm is, therefore, an appropriate choice
over the line-based algorithm for 3D raster objects,
except for the case when the objects’ shapes are sim-
ple or when the number of directions in which the
forces are computed is small. In future work, the
φ-descriptor algorithm can also be extended for 3D
raster objects, and then the processing times and per-
formance of the force histogram and the φ-descriptor
for 3D raster objects can also be comparatively com-
pared.
REFERENCES
Bourke, P. (2007). Distributing points on a sphere.
Deselaers, T., Keysers, D., and Ney, H. (2004). Fea-
tures for image retrieval: A quantitative comparison.
In Joint Pattern Recognition Symposium, pages 228–
236. Springer.
Egenhofer, M. (1990). A mathematical framework for
the definition of topological relations. In Proc. the
fourth international symposium on spatial data hand-
ing, pages 803–813.
Egenhofer, M. J. (1989). A formal definition of binary
topological relationships. In International conference
on foundations of data organization and algorithms,
pages 457–472. Springer.
Fast Fourier Transform based Force Histogram Computation for 3D Raster Data
73

Frank, A. U. (1996). Qualitative spatial reasoning: Cardi-
nal directions as an example. International Journal of
Geographical Information Science, 10(3):269–290.
Gapp, K.-P. (1995). Angle, distance, shape, and their rela-
tionship to projective relations. In Proceedings of the
17th annual conference of the cognitive science soci-
ety, pages 112–117.
Krishnapuram, R., Keller, J. M., and Ma, Y. (1993). Quan-
titative analysis of properties and spatial relations of
fuzzy image regions. IEEE Transactions on fuzzy sys-
tems, 1(3):222–233.
Matsakis, P. (1998). Relations spatiales structurelles et in-
terpretation d’images. PhD thesis.
Matsakis, P. and Wendling, L. (1999). A new way to repre-
sent the relative position between areal objects. IEEE
Transactions on pattern analysis and machine intelli-
gence, 21(7):634–643.
Miller, H. J. and Wentz, E. A. (2003). Representation and
spatial analysis in geographic information systems.
Annals of the Association of American Geographers,
93(3):574–594.
Miyajima, K. and Ralescu, A. (1994). Spatial organization
in 2d segmented images: representation and recogni-
tion of primitive spatial relations. Fuzzy Sets and Sys-
tems, 65(2-3):225–236.
Naeem, M. and Matsakis, P. (2015). Relative position
descriptors. In Proceedings of the International
Conference on Pattern Recognition Applications and
Methods-Volume 1, pages 286–295. SCITEPRESS-
Science and Technology Publications, Lda.
Ni, J. and Matsakis, P. (2010). An equivalent definition of
the histogram of forces: Theoretical and algorithmic
implications. Pattern Recognition, 43(4):1607–1617.
Ni, J., Matsakis, P., and Wawrzyniak, L. (2004). Quanti-
tative representation of the relative position between
3d objects. In VIIP 2004 (4th IASTED Int. Conf. on
Visualization, Imaging, and Image Processing), pages
452–289.
Ryoo, M. S. and Aggarwal, J. K. (2009). Spatio-temporal
relationship match: video structure comparison for
recognition of complex human activities. In ICCV,
volume 1, page 2. Citeseer.
Schneider, M. and Behr, T. (2005). Topological relation-
ships between complex lines and complex regions.
In International Conference on Conceptual Modeling,
pages 483–496. Springer.
Skubic, M., Blisard, S., Carle, A., and Matsakis, P. (2002).
Hand-drawn maps for robot navigation. In AAAI
Spring Symposium, Sketch Understanding Session,
page 23.
Skubic, M., Matsakis, P., Forrester, B., and Chronis, G.
(2001). Extracting navigation states from a hand-
drawn map. In Proceedings 2001 ICRA. IEEE In-
ternational Conference on Robotics and Automation
(Cat. No. 01CH37164), volume 1, pages 259–264.
IEEE.
Smeulders, A. W., Worring, M., Santini, S., Gupta, A., and
Jain, R. (2000). Content-based image retrieval at the
end of the early years. IEEE Transactions on Pattern
Analysis & Machine Intelligence, (12):1349–1380.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
74
