
Sclera Segmentation using Spatial Kernel Fuzzy Clustering Methods
M. S. Maheshan
1a
, B. S. Harish
1b
and S. V. Aruna Kumar
2c
1
Department of Information Science and Engineering, JSS Science and Technology University, Mysuru, Karnataka, India
2
Socia-Lab, University Beira Interior, Convento de Sto. António, Covilhã, Portugal
Keywords: Clustering, Fuzzy C Means, Sclera, Segmentation.
Abstract: Biometrics is one of the domain that is gaining lot of importance in the present digital industry. Biometrics
are getting integrated in different devices and reaching the end users at a very affordable cost. Among various
biometric traits, Sclera is one such trait that is getting popular in the research community for its distinct nature
of authenticating and identification of individuals. The recognition system using sclera trait purely depends
on efficient segmentation of sclera image. Segmentation process is considered to be significant in image
processing system because of better visualization. The segmentation can be done using region based, edge
based, threshold based and also clustering based techniques. This paper concentrates on clustering based
technique by proposing a variant of conventional Fuzzy C Means (FCM) algorithm. Though the Fuzzy C
Means presents outstanding results in many applications, unfortunately it is sensitive to noise and ignore
neighbourhood information. Thus to alleviate these limitations this paper presents Generalized Spatial Kernel
Fuzzy C Means (GSK-FCM) clustering algorithms for sclera segmentation. To evaluate the proposed methods,
experimentation are conducted on Sclera Segmentation and Recognition Benchmarking Competition (SSRBC
2015) dataset. The result of the experiments reveals that the proposed methods outperform the other variants
of FCM.
1 INTRODUCTION
In today’s mobile based tech industry, biometric
based technological platforms are the front runners in
applying technologies to various devices. Biometric
has lately received a lot of attraction in popular media
including commercial applications. The requirement
to validate ourselves to machines is always increasing
in today’s networked society, which in turn helps in
closing the gap between the humans and the machines
to secure the transactions and networks. Biometric
deals with identification of persons based on their
biological or behavioural distinctiveness (Jain et al.,
2000). Amongst the various biometric traits available,
this paper presents about sclera segmentation. Sclera
which is the white part of the eye that surrounds the
cornea, occupies more than 80% of the surface area
of the eyeball. This trait when compared to other
traditional traits is hard to spoof as the optic nerves of
the sclera region are very unique and random
including the identical twins. In addition the patterns
a
https://orcid.org/0000-0002-3330-8795
b
https://orcid.org/0000-0001-5495-0640
c
https://orcid.org/0000-0002-8953-2921
of these nerves remain factual till the life-time of a
person (Joussen, 2001). Sclera segmentation is a
significant procedure in sclera recognition process.
Segmentation partition the image into its
constituent’s parts and groups the uniform pixels into
clusters. Segmentation techniques have been used in
wide range of medical image processing such as
thresholding (Otsu, 1979), region growing (Adams et
al., 1994; Beveridge et al., 1989) and clustering (Ng
et al., 2006; Chen et al., 1998; Wang el al., 2006;
Hadjahmadi et al., 2008). Clustering has been
extensively applied in numerous fields’ such as
geology, taxonomy, medical image processing,
engineering systems. Among various clustering
techniques the most widely used techniques include
the k-means, fuzzy c-means (Wang el al., 2006) and
their variants. The traditional fuzzy c-means
clustering algorithm is found to comprise the pixel
attributes. This process was found to fail in providing
efficient results in the presence of corrupted noise in
the image. Therefore, from the existing research it is
Maheshan, M., Harish, B. and Kumar, S.
Sclera Segmentation using Spatial Kernel Fuzzy Clustering Methods.
DOI: 10.5220/0008935704330439
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 433-439
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
433

observed that the significance to improve the
performance of the standard FCM is essential.
Recently, several researchers have developed
diverse methods by modifying the objective function
or membership function of standard FCM method
(Liew et al., 2001; Ahmed et al., 2001). Also, it was
seen that traditional FCM, which uses Euclidean
distance is used to determine the distance between
cluster center and data. The above algorithm was
found to be limited in revealing non-Euclidean
structure of the input data. To overcome this problem,
researchers modified the existing approaches in such
a way that it improves the performance. Further,
several researchers developed a novel FCM method
where kernel function is employed to determine the
distance between center of the cluster and data pixel
(Chen et al., 2002). For better result, a hybrid
technique is proposed which provide new robust
clustering algorithm. In this technique, kernelized
fuzzy logic is incorporated with spatial constraint
which results in new clustering method called
SKFCM. By introducing the higher and lower
elimination of non-required data belonging to one
cluster can be removed. Since FCM failed to handle
the small differences between clusters and as it is
sensitive to noise, FCM algorithm was derived into
KFCM which is based on kernel method. Due to the
limitations of this algorithm a robust generalized
spatial kernel fuzzy C-Means clustering method is
introduced in this research work.
2 BACKGROUND STUDY
Fuzzy C-Means (FCM), a method of clustering
technique which maps each data point to two or more
clusters and showcases very good results in many
applications in the field of medicine, engineering,
economics, psychology and many other disciplines
(Ben-Dor et., 1999).
Consider
12
= { , ,...... ,...... }
in
X
xx x x
e the
n data
points and
12
= { , ,...... ,...... }
jc
Vvv v v
be the set of c
cluster centers. The objective of FCM is to partition
the data points into
c group such that the data points
present in the same group have similar characteristics
when compared to the data points present in the other
groups by reducing the objective function as shown
in equation 1.
2
=1 =1
=
nc
m
ijji
ji
J
uxv
(1)
where
m
refers to fuzzifier value,
i
v
refers to
th
i
cluster center,
[0,1]
ij
u
is the membership of the
data point
j
x
to the
th
i
cluster center and
.
is the
distance measure used to compute the distance
between data point
)(
j
x
and cluster center
)(
i
v
.
Fuzzy C-Means is an iterative algorithm which
updates the membership
)(
ij
u
and cluster centers
using following equations.
1
1
=1
1
=
ij
m
c
ji
k
jk
u
xv
xv
(2)
=1
=1
=
n
m
ij j
j
i
n
m
ij
j
ux
v
u
(3)
The Fuzzy C-Means process starts by randomly
picking the
c
number of data points as initial cluster
centers. Furthermore, the membership value is
computed based on the distance of the data point
j
x
to the cluster center
i
v
using equation 2. In the
following step, the objective function value is
computed based on previously evaluated membership
values using equation 1. The cluster centers are then
updated based on the membership values of each data
points using equation 3. This iterative process is
stopped when the difference of successive iterations
objective function value is less than the user specified
stopping criterion value. Although Fuzzy C-Means is
found to be an important tool for image processing by
producing outstanding results it has its own
limitations, such as sensitivity to noise and ignorance
of neighborhood information (Bezdek, 1994). The
use of euclidian distance metric in FCM inturn
degrades the clustering results (Koza, 1994). Kernal
FCM (KFCM) an alternative method was introduced
to overcome the noise sensitivity problem in the
traditional Fuzzy C-Means (Despotović et al., 2015).
Unlike the traditional FCM which makes use of
euclidian distance metric, the kernal FCM uses kernel
distance function which minimizes the impact of
noise. However, the limitation in the Kernal FCM is
that it do not utilize the neighbourhood information.
To overcome this problem, researchers propsed a
variant of FCM known as Spatial Kernel FCM
(SKFCM) (Timmis et al., 2008; Roy et al., 2014).
This technique incorporates neighbourhood
information into objective function of FCM. To
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
434

certain extent the above techniques overcome the
drawbacks of Fuzzy C-Means. However they still
suffer from single feature inputs and high
computational time. To address these limitations, a
Robust Spatial Kernel FCM (RSKFCM) algorithm
was proposed in (Kumar et al., 2015). Robust Spatial
Kernel FCM (RSKFCM) consists of spatial
information to the conventional FCM function.
Similar to FCM, the main aim of the RSKFCM is to
minimize the objective function shown in equation 4.
2
=1 =1
=()()
cn
m
ij j i
ij
Jwxv
(4)
Where
c is the number of clusters, n is the number
of data points,
m is a constant, which controls the
fuzziness of the resulting partition,
ij
w
is the
RSKFCM membership degree of
j
x
in
th
i
cluster.
i
v
is the i
th
cluster center,
is an implicit non
linear map which is computed as:
2
() ()=(,) (,)2(,)
j
ijjjjji
x
vKxxKvvKxv
(5)
where
K
is the inner product of kernel function
i.e.,
)()(=),( yxyxK
T
.
2
2
(, )=exp /Kxy x y
(6)
In Gaussian kernel
1=),( xxK
and
1=),( vvK
,
hence the kernel function becomes:
2
( ) ( ) = 2(1 ( , ))
j
iji
x
vKxv
(7)
Substituting equation 7 in equation 4, the objective
function becomes:
=1 =1
= 2 (1 ( , ))
cn
m
ij j i
ij
J
wKxv
(8)
RSKFCM membership function
ij
w
is the
combination of kernel membership function
ij
u
and
neighbourhood function
ij
s
and it is computed as:
=1
=
pq
ij ij
ij
c
pq
kj kj
k
us
w
us
(9)
where
p and q are parameter to control the relative
importance of kernel membership and neighbourhood
membership functions.The kernel and neighbourhood
membership functions are computed using equation
10 and 11.
1/( 1)
1/( 1)
=1
1,
=;
1,
m
ji
ij
c
m
jk
k
Kx v
u
Kx v
(10)
()
=
ij ik
kNKx
j
s
u
(11)
where
)(
jk
xN
represents a neighbourhood data
points of
j
x
. This neighbourhood function
represents the probability that data point
j
x
belongs
to
th
i
cluster.
Similar to FCM, RSKFCM also work in iterative
process by updating the membership and cluster
center values. The cluster centers are updated using
equation 12
=1
=1
(,)
=
(,)
n
m
ij j i j
j
i
n
m
ij j i
j
wKx vx
v
wKx v
(12)
This iterative of RSKFCM will stop when stopping
criteria is satisfied i.e., the difference of successive
iterations objective function value is less than the user
specified stopping criteria value. Though RSKFCM
solved the problems of single feature inputs and high
computational time, it still holds few limitations:
Firstly, incorporating neighborhood information
only to the objective function.
Secondly, the current methods assume that, all
features have equal importance. However, in real
world cases all the features may not be equally
important.
To alleviate these drawbacks, Generalized Spatial
Kernel Fuzzy C-Means (GSKFCM) is proposed in
this article.
3 PROPOSED METHOD
Generalized Spatial Kernel Fuzzy C-Means (GSK-
FCM) incorporates the weighted neighborhood
information into distance function and uses Gaussian
kernel as distance metric.
The aim of the GSK-FCM is to minimize the
objective function shown in equation 13
2
=1 =1
=2 ,
cn
m
ij new j k
ij
J
zd xv
(13)
Sclera Segmentation using Spatial Kernel Fuzzy Clustering Methods
435

where
ij
z
is the GSK-FCM membership function
and it is computed as:
1
2
1
2
=1
1
=
,
,
ij
c
m
new j i
new j k
k
z
dxv
dxv
(14)
Where
new
d
is the GSK-FCM distance function
which incorporates the neighbourhood function into
distance function and it is computed as:
22
,= ,
new j i j i ij
dxvdxvfp
(15)
where,
ij
vxd ,
2
is the Gaussian Kernel distance
function shown in equation 7 and
1
()=
ij
ij
fp
p
is the
neighborhood function.
GSK-FCM considers neighbourhood information
and computes membership value associated with each
data point as weighted sum of traditional FCM
membership value and the membership value of the
k
N
neighbour points. The neighbourhood function
)(
ij
p
is defined as
=0
=,
N
k
ij j k ik
k
p
hx x gu
(16)
Where
k
N
is the number of neighbourhood data
points,
ikik
uug =)(
is the membership function
(equation 10),
),(
kj
xxh
is the distance function
which is computed as:
1
2
2
=0
,
,=
,
N
k
jk
jk
jl
l
dxx
hx x
dxx
(17)
Substituting equation 17 in 16 the neighbourhood
function becomes:
1
2
2
=0 =0
,
=
,
NN
kk
jk
ij ik
jl
kl
dxx
pgu
dxx
(18)
Substituting equation 15 in equation 14, the
membership function
ij
z
becomes,
1
1
2
1
2
=1
,
=
,
c
m
ji ij
ij
jk jk
k
dxvfp
z
dxv fp
(19)
1
1
21
1
1
2
=1
1
1
21
1
1
2
=1 =1
,
,
=
,
,
c
m
ji
m
ij
jk
k
cc
m
ji
m
jk
jl
kl
dxv
fp
dxv
dxv
fp
dxv
(20)
where,
1
1
2
1
2
=1
,
=
,
c
m
ji
ij
jk
k
dxv
u
dxv
Then the membership function
ij
z
becomes
1
1
1
1
=1
=
m
ij ij
ij
c
m
jk jk
k
uf p
z
uf p
(21
)
Similar to FCM and RSKFCM, GSKFCM operates in
iterative process by updating membership and cluster
center value. The cluster centers are updated using
equation 22
=1
=1
,
=
,
n
m
ij j i j
j
i
n
m
ij j i
j
zKxv x
v
zKxv
(22)
GSK-FCM decides the label based on the maximum
membership value.
4 DATASET AND RESULT
ANALYSIS
This section presents the result evaluated of the
proposed GSK-FCM clustering algorithm. To
evaluate the proposed method, experimentations are
conducted using Sclera Segmentation and
Recognition Benchmarking Competition
(SSRBC2015) dataset (Das et al., 2016). Table 1
presents the characteristics of the dataset. The dataset
contains 30 individuals eye image with different cases
such as blinked eye, closed eye, blurred eye. For
every individual eye, the images are captured in
different angles like looking at the center, left, right
and up. Thus the dataset in total consists of 120 eye
images with ground truth images.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
436
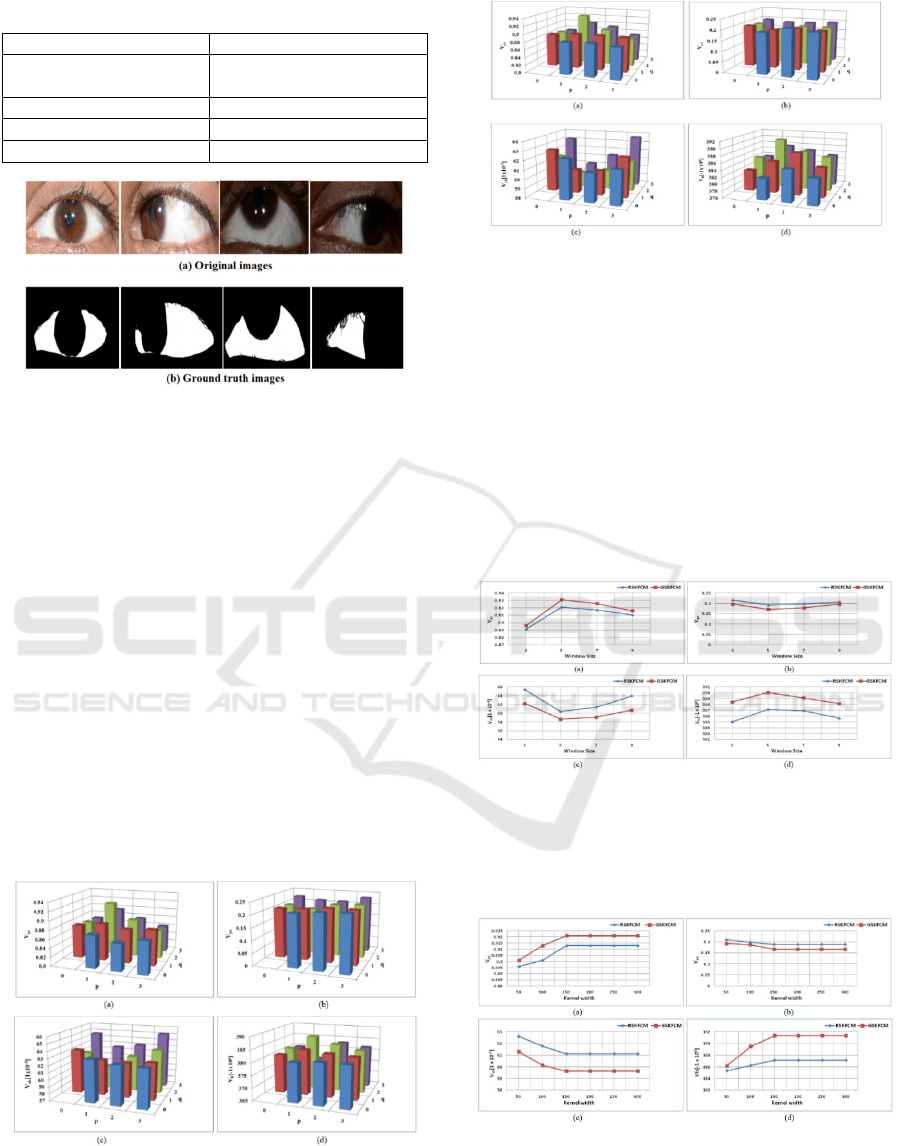
Table 1: Characteristics of SSRBC2015 dataset.
Number of individuals 30
Number of samples per
individuals
4
Captured Angle Center,left, right and up
Image resolution 1489 X 1105
Total number of samples 120
Figure 1: Sample sclera images and ground truth of
SSRBC2015 dataset.
To test the effectiveness of the proposed model, the
performance of the GSK-FCM method is compared
with other versions of FCM and RSKFCM. To find
the optimal value of the parameters, four well known
cluster validity indices: Partition Coefficient
pc
V
,
Partition Entropy
pe
V
, Fukuyama-Sugeno function
fs
V
, Xie-Beni function
xb
V
are used as an
evaluation metrics. For all the experiments, we have
set the fuzzifier m value to 2 and stopping criteria
to 0.00001 empirically. For sclera segmentation,
cluster number
c
is set to 3 (sclera, iris and outer
region). Figure 2 and Figure 3 presents the cluster
validity results of the existing RSKFCM and
proposed GSK-FCM method for different
p
and
q
values.
Figure 2: Cluster validity indices for different p and q
values of RSKFCM on sclera segmentation (a)
pc
V
, (b)
pe
V
, (c)
xb
V
, (d)
fs
V
.
Figure 3: Cluster validity indices for different p and q
values of GSKFCM on sclera segmentation (a)
pc
V
, (b)
pe
V
, (c)
xb
V
, (d)
fs
V
.
Figure 4 and Figure 5 presents the comparison of
four cluster validity indices values of the proposed
methods for different window size on sclera
segmentation. From empirical evaluation, it is found
1=p
,
2=q
,
= 150
and window size=5 are
optimal values for sclera segmentation. Table 2 and
Table 3 shows the cluster validity indices value,
precision and recall values of the proposed methods.
Figure 4: Cluster validity indices for different window size
of the existing RSKFCM and proposed GSK-FCM methods
on sclera segmentation (a)
pc
V
, (b)
pe
V
, (c)
xb
V
, (d)
fs
V
.
Figure 5: Cluster validity indices for different kernel width
of the existing RSKFCM and proposed GSK-FCM
methods on sclera segmentation (a)
pc
V
, (b)
pe
V
, (c)
xb
V
, (d)
fs
V
.
Sclera Segmentation using Spatial Kernel Fuzzy Clustering Methods
437

Table 2: Performance comparision in terms of cluster
validity indices on sclera traits.
Method Precision Recall
FCM 65.98 65.12
KFCM 67.43 66.96
SFCM 69.72 68.79
SKFCM 72.93 73.08
RSKFCM 85.21 80.21
GSK-FCM 85.89 80.23
Table 3: Performance comparision in terms of
segmentation on sclera traits.
Method V
pc
V
pe
V
xb
[1x10
-3
] V
fs
[-1x10
6
]
FCM 0.832
0.236 74.68
350.64
KFCM 0.848
0.225 72.19
353.68
SFCM 0.866
0.220 70.68
361.31
SKFCM 0.884
0.213 67.84
365.38
RSKFCM 0.921 0.192 60.34 387.13
GSK-FCM 0.931 0.167 59.65 390.67
5 CONCLUSION
This paper presents the Generalized Spatial Kernel-
Fuzzy C Means (GSK-FCM) clustering algorithm
which is capable of segmenting sclera images. The
proposed algorithm have overcome the drawbacks of
traditional FCM method by considering
neighbourhood information and using Gaussian
kernel distance measure. The inclusion of
neighbourhood information and use of kernel
function reduces the impact of noise which in turn
increases the results. This paper work has been
applied to sclera segmentation images, where in the
segmentation plays a crucial role for
recognition/identification purpose for future
researchers who deal in authentication of users using
sclera biometric trait. From the observations of the
results and its comparison with other methods the
proposed GSK-FCM performs better than the other
methods.
REFERENCES
Adams, R., & Bischof, L. (1994). Seeded region growing.
IEEE Transactions on pattern analysis and machine
intelligence, 16(6), 641-647.
Ahmed, M. N., Yamany, S. M., Mohamed, N., Farag, A. A.,
& Moriarty, T. (2002). A modified fuzzy c-means
algorithm for bias field estimation and segmentation of
MRI data. IEEE transactions on medical imaging,
21(3), 193-199.
Ben-Dor, A., Shamir, R., & Yakhini, Z. (1999). Clustering
gene expression patterns. Journal of computational
biology, 6(3-4), 281-297.
Beveridge, J. R., Griffith, J., Kohler, R. R., Hanson, A. R.,
& Riseman, E. M. (1989). Segmenting images using
localized histograms and region merging. International
Journal of Computer Vision, 2(3), 311-347.
Bezdek, J. C. (1994). What is computational intelligence?
(No. CONF-9410335-). USDOE Pittsburgh Energy
Technology Center, PA (United States); Oregon State
Univ., Corvallis, OR (United States). Dept. of
Computer Science; Naval Research Lab., Washington,
DC (United States); Electric Power Research Inst., Palo
Alto, CA (United States); Bureau of Mines,
Washington, DC (United States).
Chen, C. W., Luo, J., & Parker, K. J. (1998). Image
segmentation via adaptive K-mean clustering and
knowledge-based morphological operations with
biomedical applications. IEEE transactions on image
processing, 7(12), 1673-1683.
Chen, D. Z. S. (2002). Fuzzy clustering using kernel
method. IEEE, Nanjing.
Chen, J. H., & Chen, C. S. (2002). Fuzzy kernel perceptron.
IEEE Transactions on Neural Networks, 13(6), 1364-
1373.
Das, A., Pal, U., Ferrer, M. A., & Blumenstein, M. (2016,
June). SSRBC 2016: Sclera segmentation and
recognition benchmarking competition. In 2016
International Conference on Biometrics (ICB) (pp. 1-
6). IEEE.
Despotović, I., Goossens, B., & Philips, W. (2015). MRI
segmentation of the human brain: challenges, methods,
and applications. Computational and mathematical
methods in medicine, 2015.
Hadjahmadi, A. H., Homayounpour, M. M., & Ahadi, S. M.
(2008, June). Robust weighted fuzzy c-means
clustering. In 2008 IEEE International Conference on
Fuzzy Systems (IEEE World Congress on
Computational Intelligence) (pp. 305-311). IEEE.
Jain, A., Hong, L., & Pankanti, S. (2000). Biometric
identification. Communications of the ACM, 43(2), 90-
98.
Joussen, A. M. (2001). Vascular plasticity–the role of the
angiopoietins in modulating ocular angiogenesis.
Graefe's Archive for Clinical and Experimental
Ophthalmology, 239(12), 972-975.
Koza, J. R. (1994). Genetic programming II: Automatic
discovery of reusable subprograms. Cambridge, MA,
USA, 13(8), 32.
Kumar, S. A., Harish, B. S., & Guru, D. S. (2015, March).
Segmenting MRI brain images using evolutionary
computation technique. In 2015 International
Conference on Cognitive Computing and Information
Processing (CCIP) (pp. 1-6). IEEE.
Liew, A. C., & Yan, H. (2001, June). An adaptive fuzzy
clustering algorithm for medical image segmentation.
In Proceedings International Workshop on Medical
Imaging and Augmented Reality (pp. 272-277). IEEE.
Ng, H. P., Ong, S. H., Foong, K. W. C., Goh, P. S., &
Nowinski, W. L. (2006, March). Medical image
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
438

segmentation using k-means clustering and improved
watershed algorithm. In 2006 IEEE Southwest
Symposium on Image Analysis and Interpretation (pp.
61-65). IEEE.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE transactions on systems, man,
and cybernetics, 9(1), 62-66.
Roy, S., Carass, A., Prince, J. L., & Pham, D. L. (2014,
September). Subject specific sparse dictionary learning
for atlas based brain MRI segmentation. In
International Workshop on Machine Learning in
Medical Imaging (pp. 248-255). Springer, Cham.
Timmis, J., Hone, A., Stibor, T., & Clark, E. (2008).
Theoretical advances in artificial immune systems.
Theoretical Computer Science, 403(1), 11-32.
Wang, W., Zhang, Y., Li, Y., & Zhang, X. (2006, June).
The global fuzzy c-means clustering algorithm. In 2006
6th World Congress on Intelligent Control and
Automation Vol. 1, pp. 3604-3607 IEEE.
Sclera Segmentation using Spatial Kernel Fuzzy Clustering Methods
439
