Multimodal Deep Denoising Convolutional Autoencoders for Pain
Intensity Classification based on Physiological Signals
Patrick Thiam
1,2 a
, Hans A. Kestler
1 b
and Friedhelm Schwenker
2
1
Institute of Medical Systems Biology, Ulm University, Albert-Einstein-Allee 11, 89081 Ulm, Germany
2
Institute of Neural Information Processing, Ulm University, James-Franck-Ring, 89081 Ulm, Germany
Keywords:
Pain Intensity Classification, Information Fusion, Autoencoder, Convolutional Neural Networks.
Abstract:
The performance of a conventional information fusion architecture is greatly affected by its ability to detect
and combine useful and complementary information from heterogeneous representations stemming from a set
of distinctive modalities. Moreover, manually designing a set of relevant and complementary features for a
specific pattern recognition task is a complex and tedious endeavour. Therefore, enabling pattern recognition
architectures to autonomously generate and select relevant descriptors directly from the set of preprocessed
raw data is a favourable alternative to the more conventional manual feature engineering. In the follow-
ing work, multimodal information fusion approaches based on Deep Denoising Convolutional Autoencoders
(DDCAEs) are proposed for the classification of pain intensities based on physiological signals (electrodermal
activity (EDA), electromyogram (EMG) and electrocardiogram (ECG)). The approaches are characterized by
the simultaneous optimization of both the joint representation of the input channels generated by the multi-
modal DDCAE and the feed-forward neural network performing the classification of the pain intensities. The
assessment performed on the BioVid Heat Pain Database (Part A) points at the relevance of the proposed ap-
proaches. In particular, the introduction of trainable weighting parameters for the generation of an aggregated
latent representation outperforms most of the previously proposed methods in related works, each based on a
set of carefully selected hand-crafted features.
1 INTRODUCTION
Multimodal information fusion seeks to improve the
performance of an inference model by smartly com-
bining useful information extracted from a set of dis-
tinctive modalities (e.g. speech, text, video or phys-
iological channels). Conventional information fusion
architectures are therefore built upon a set of care-
fully engineered representations extracted individu-
ally from each involved modality (Kessler et al., 2017;
Thiam and Schwenker, 2017; Bellmann et al., 2018;
Thiam et al., 2018). Hence, the performance of the
designed architecture depends on its ability to suc-
cessfully combine the resulting set of heterogeneous
representations. However, since each representation
is specific to a single modality and is generated inde-
pendently from the others, finding the right approach
for an effective multimodal information aggregation
can be very tedious. Moreover, manually designing a
a
https://orcid.org/0000-0002-6769-8410
b
https://orcid.org/0000-0002-4759-5254
relevant representation for a specific modality is com-
plex and time consuming.
Consequently, a steadily growing amount of work has
been focusing on applying deep learning approaches,
in order to enable a system to autonomously learn an
effective joint representation of multiple modalities
(Vukoti
´
c et al., 2016; Ben Said et al., 2017), thereby
taking in account the complementarity of the informa-
tion shared between the modalities, as well as the per-
formance of the resulting joint representation (Haiyan
et al., 2015; Le et al., 2018). There are mainly two
ideas behind most of the proposed approaches: the
first idea consists of generating a joint latent represen-
tation from the input modalities, and the second idea
consists of learning separate representations for each
input modality while maximizing the correlation be-
tween the generated representations. For example, the
authors in (Liu et al., 2019a) propose a MUltimodal
Convolutional AutoEncoder (MUCAE) approach to
learn robust representations from visual and textual
modalities by exploiting the correlation between the
latent representations of the modality specific autoen-
Thiam, P., Kestler, H. and Schwenker, F.
Multimodal Deep Denoising Convolutional Autoencoders for Pain Intensity Classification based on Physiological Signals.
DOI: 10.5220/0008896102890296
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 289-296
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
289

coders. In (Yang et al., 2017), the authors propose a
Correlational Recurrent Neural Network (CorrRNN)
for fusing multiple input modalities which are inher-
ently temporal in nature. The proposed approach
basically consists of a multimodal autoencoder with
integrated recurrent neural networks combined with
dynamic weighting modules. The whole architec-
ture is optimized not just by reducing the reconstruc-
tion error, but also by maximizing the correlation be-
tween its inputs while performing a dynamic weight-
ing across the modality representations.
Moreover, several works have been taking advantage
of the end-to-end joint training of autoencoders and
classifiers to improve the performance of specific pat-
tern recognition systems. In (Liu et al., 2019b), the
authors propose a classification architecture consist-
ing of the joint optimization of a 1-D denoising con-
volutional autoencoder and a 1-D convolutional neu-
ral network for the diagnosis of faulty rotating ma-
chinery, based on noisy input signals. The authors in
(Khattar et al., 2019) propose an end-to-end bimodal
fake news detection network based on the joint op-
timization of a variational autoencoder and a binary
classifier (which classifies a specific content as being
fake or not fake), based on text and images extracted
from tweets’ content. In (Ditthapron et al., 2019), the
authors propose an Event-Related Potential Encoder
Network (ERPENet) for the classification of attended
and unattended events (Squires et al., 1975), based
on electroencephalography (EEG) signals. The pre-
sented network consists of a jointly trained multi-task
autoencoder and an event classifier.
Meanwhile, there is a growing amount of work focus-
ing specifically on pain recognition based on physio-
logical signals. However, most of the related works
are based on a set of carefully designed features, and
rely on more conventional information fusion strate-
gies such as early or late fusion to perform the corre-
sponding classification tasks. In (Werner et al., 2014;
K
¨
achele et al., 2016b), the authors extract several dis-
tinctive features from each input channel (EDA, ECG,
EMG) and perform the classification of several lev-
els of heat-induced pain intensity using early fusion
in combination with a Random Forest classification
model (Breiman, 2001).
The authors in (Chu et al., 2017) also perform early
fusion combined with feature selection based on ge-
netic algorithms in order to extract the most interest-
ing set of features from all input channels (Skin Con-
ductance (SCL), ECG, Blood Volume Pulse (BVP)).
The classification is subsequently performed using ei-
ther a Support Vector Machine (SVM) (Abe, 2005),
a k-Nearest Neighbour (k-NN) algorithm or a Linear
Discriminant Analysis (LDA) model (Fisher, 1936).
In (Lim et al., 2019), the authors propose a bagged
ensemble of Deep Belief Networks (DBNs) (Lopes
and Ribeiro, 2015) for the assessment of patient’s
pain level during surgery, using photoplethysmogra-
phy (PPG). The ensemble of bagged DBNs is also
trained on a set of hand-crafted features.
In the current work, several end-to-end multimodal
DDCAE approaches are proposed for the assessment
and classification of pain intensities based on mea-
surable physiological parameters (EDA, EMG, ECG).
The aim of the current work is to significantly im-
prove the generalization ability of the pain classifi-
cation system by learning a joint and discriminative
latent representation from the three input channels,
while simultaneously optimizing a specific pain inten-
sity inference model. The remainder of the work is or-
ganized as follows. The proposed approaches are de-
scribed in Section 2. A description of the performed
experiments as well as the corresponding results is
provided in Section 3, and the work is concluded in
Section 4 with a short discussion and a description of
potential future works.
2 PROPOSED APPROACHES
A DDCAE has the same basic structure as a conven-
tional autoencoder (Hinton and Zemel, 1993; Hin-
ton and Salakhutdinov, 2006), which consists of an
encoder and a decoder. Both encoder and decoder
are feed-forward neural networks, whereas the en-
coder maps its input into a latent representation, while
the decoder reconstructs the encoder’s input based on
the computed latent representation. In the case of
a DDCAE, the feed-forward neural networks com-
prise multiple convolutional, pooling and upsampling
layers. Moreover, the network’s input consists of a
corrupted input signal (e.g., the corrupted signal can
be computed by adding Gaussian noise to the uncor-
rupted signal) and the network is trained to recon-
struct the clean uncorrupted input signal. The param-
eters of the encoder and decoder networks are there-
fore trained to minimize the reconstruction error be-
tween the decoder’s output and the uncorrupted input
signal. This results into a robust latent representation
that can be subsequently used to train an inference or
clustering model, depending on the task at hand.
In the current work, several fusion architectures char-
acterized by the generation of a robust joint represen-
tation of several input channels based on DDCAEs,
while simultaneously optimizing an inference model
based on the computed joint latent representation, are
proposed. Depending on the procedure used to gen-
erate the joint representation of the input channels,
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
290

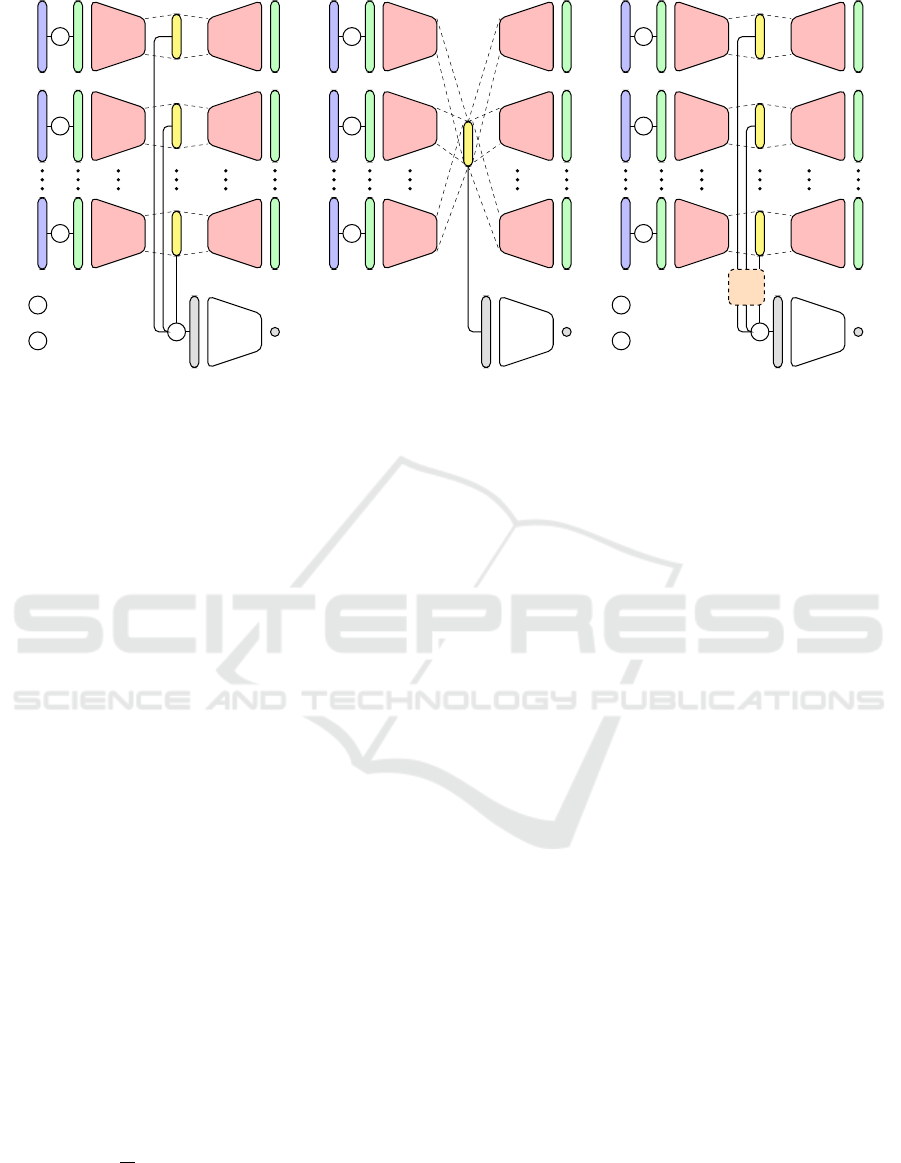
X
0, j
X
1, j
X
n, j
N
N
N
e
X
0, j
e
X
1, j
e
X
n, j
Encoder
f
θ
0
(
e
X
0, j
)
Encoder
f
θ
1
(
e
X
1, j
)
Encoder
f
θ
n
(
e
X
n, j
)
h
0, j
h
1, j
h
n, j
Decoder
g
φ
0
(h
0, j
)
Decoder
g
φ
1
(h
1, j
)
Decoder
g
φ
n
(h
n, j
)
e
X
0
0, j
e
X
0
1, j
e
X
0
n, j
C
h
j
Classifier
f
ψ
(h
j
)
y
j
N
Gaussian
Noise
C
Concatenation
(a) Latent representation concatenation.
X
0, j
X
1, j
X
n, j
N
N
N
e
X
0, j
e
X
1, j
e
X
n, j
Encoder
f
θ
0
(
e
X
0, j
)
Encoder
f
θ
1
(
e
X
1, j
)
Encoder
f
θ
n
(
e
X
n, j
)
h
Decoder
g
φ
0
(h)
Decoder
g
φ
1
(h)
Decoder
g
φ
n
(h)
e
X
0
0, j
e
X
0
1, j
e
X
0
n, j
h
j
Classifier
f
ψ
(h
j
)
y
j
(b) Shared latent representation.
X
0, j
X
1, j
X
n, j
N
N
N
e
X
0, j
e
X
1, j
e
X
n, j
Encoder
f
θ
0
(
e
X
0, j
)
Encoder
f
θ
1
(
e
X
1, j
)
Encoder
f
θ
n
(
e
X
n, j
)
h
0, j
h
1, j
h
n, j
Decoder
g
φ
0
(h
0, j
)
Decoder
g
φ
1
(h
1, j
)
Decoder
g
φ
n
(h
n, j
)
e
X
0
0, j
e
X
0
1, j
e
X
0
n, j
Gating
Layer
+
+
+
h
j
Classifier
f
ψ
(h
j
)
y
j
•
Element-wise
Product
+
+
+
Element-wise
Sum
(c) Gated latent representation.
Figure 1: Fusion architectures based on DDCAEs, trained simultaneously with an additional neural network performing the
classification task.
one can distinguish three basic and distinctive archi-
tectures (see Figure 1).
The first architecture is depicted in Figure 1a and con-
sists of learning simultaneously a single latent repre-
sentation for each channel, while using a concatena-
tion of all channel specific latent representations to
train the classifier. For each channel i ∈ N, a noisy
input signal
e
X
i, j
(with 1 ≤ j ≤ N, N ∈ N represents
the total number of training samples) is first generated
based on the uncorrupted signal X
i, j
∈ R
m
i
(m
i
∈ N
represents the dimensionality of the signal stemming
from the i
th
modality). The noisy signal is subse-
quently fed into the encoder f
θ
i
(θ
i
corresponds to the
set of trainable parameters of the encoder specific to
the i
th
channel), in order to generate a channel specific
latent representation h
i, j
:
h
i, j
= f
θ
i
(
e
X
i, j
) (1)
. The latent representation is further fed into the de-
coder g
φ
i
, which generates an output
e
X
0
i, j
:
e
X
0
i, j
= g
φ
i
(h
i, j
) (2)
. The parameters of the channel specific DDCAE are
trained to minimize the reconstruction error between
the decoder’s output
e
X
0
i, j
and the uncorrupted input
signal X
i, j
. In the current work, we use the mean
squared error function:
E
i
=
1
N
N
∑
j=1


X
i, j
−
e
X
0
i, j


2
2
+ λ


W
i


2
2
(3)
where λ


W
i


2
2
represents the regularization term
(with W
i
representing the set of all trainable param-
eters in the latent representation layer of the i
th
chan-
nel). The latent representations of all channels are fur-
ther concatenated into a single representation h
j
∈ R
d
and used in combination with the corresponding la-
bel y
j
for the optimization of an inference model f
ψ
.
In the current work, the inference model consists of a
feed-forward neural network that is trained using the
cross entropy loss function:
L
c
= −
c
∑
j=1
y
j
log(
b
y
j
) (4)
where c ∈ N is the number of classes for a specific
classification task, y
j
is the ground-truth label value
and
b
y
j
is the classifier’s output. The parameters of
the entire architecture are subsequently optimized by
minimizing the following objective function:
L =
n
∑
i=0
α
i
E
i
+ α
c
L
c
(5)
where the parameters α
i
and α
c
are regularization
weights assigned to each error function.
The second architecture depicted in Figure 1b, has
a similar structure as the first architecture (see Fig-
ure 1a) with the only difference being a single and
shared representation for all input channels (instead
of one latent representation for each input channel).
The joint latent representation is simultaneously used
to optimize the classifier. The whole architecture is
trained using the same loss function depicted in Equa-
tion 5.
The third architecture depicted in Figure 1c, also
consists of learning a single latent representation for
each channel. However, a gating layer (see Figure 2)
Multimodal Deep Denoising Convolutional Autoencoders for Pain Intensity Classification based on Physiological Signals
291

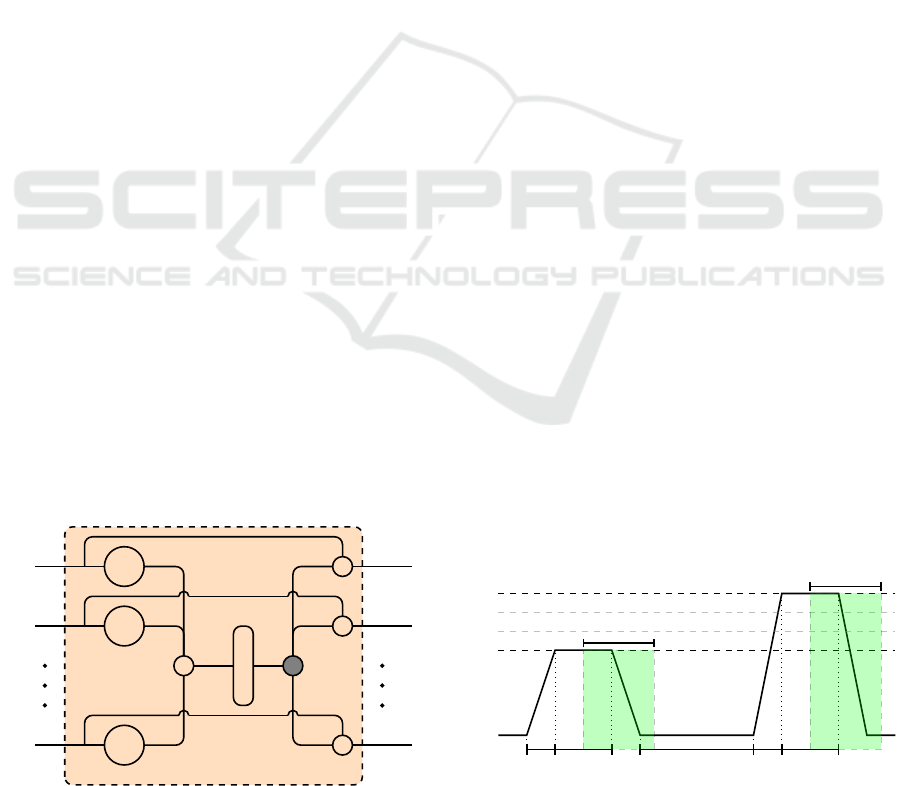
is used to generate a single weighted representation
of the channel specific latent representations before
it is used to train the classifier. For each channel i,
h
i, j
∈ R
d
i
, where d
i
∈ N represents the dimensional-
ity of the i
th
latent representation. For this specific
approach, it is required that all latent representations
have the same dimensionality: ∀i ∈ {0, 1, . . . , n}, d
i
=
η ∈ N. Furthermore, in order to simplify the follow-
ing equations, the latent representation generated for
each channel i will be referred to by h
i
(we remove
the index j of the training samples).
Each latent representation first go through a layer with
a tanh activation function:
u
i
= tanh(W
i
h
i
+ b
i
) (6)
with the output u
i
∈ [−1, 1]
η
and the trainable pa-
rameters W
i
∈ R
η×η
and b
i
∈ R
η
. The resulting out-
puts are subsequently concatenated into a single vec-
tor u = [u
0
, u
1
, . . . , u
n
] ∈ [−1, 1]
(n+1)η
. The weights of
the corresponding components are finally generated
by using a layer with a so f tmax activation function:
ω = so f tmax(W
ω
u + b
ω
) (7)
with the output ω = [ω
0
, ω
1
, . . . , ω
n
] ∈ [0, 1]
(n+1)η
(∀i, ω
i
∈ [0, 1]
η
), and the trainable parameters W
ω
∈
R
(n+1)η×(n+1)η
and b
ω
∈ R
(n+1)η
. The final latent rep-
resentation is generated through a weighted sum of all
channel specific latent representation (h
i
), using the
computed weights (ω
i
):
h =
n
∑
i=1
(h
i
 ω
i
) (8)
where  denotes the element-wise product and h ∈
R
η
is the resulting representation, which is sub-
sequently fed to the classifier f
ψ
to perform the
classification. The parameters of the gating layer
(W
i
,W
ω
, b
i
, b
ω
) are simultaneously trained with those
of the DDCAEs and those of the classifier, using the
same loss function depicted in Equation 5.
h
0
h
1
h
n
tanh
tanh
tanh
C
so f tmax
•
•
•
Figure 2: Gating Layer.
3 EXPERIMENTS
The following section provides a short description of
the dataset used for the evaluation of the presented ap-
proaches, followed by a description of the performed
experiments and the corresponding results.
3.1 BioVid Heat Pain Dataset (Part A)
The presented approaches are evaluated on the BioVid
Heat Pain Database (Part A) (Walter et al., 2013),
which is a multi-modal database consisting of 87 indi-
viduals submitted to four individually calibrated lev-
els of heat-induced pain (T
1
, T
2
, T
3
, T
4
). Several
modalities were recorded during the experiments in-
cluding video streams, EMG, ECG and EDA signals.
The current work focuses uniquely on the recorded
physiological signals (EMG, ECG, EDA). Each sin-
gle level of heat-induced pain was randomly elicited
a total of 20 times. Each of the elicitation lasted 4
seconds (sec), followed by a recovery phase of a ran-
dom length of 8 to 12 sec (see Figure 3). The base-
line temperature T
0
, corresponds to the temperature
applied during the recovery phase (32
◦
C). Therefore,
each of the 87 individuals is represented by a total
of 20 × 5 = 100 samples. The unprocessed dataset
consists of a total of 87 × 100 = 8700 samples, each
labelled with its corresponding level of heat-induced
pain elicitation (T
0
, T
1
, T
2
, T
3
, T
4
).
3.2 Data Preprocessing
In order to reduce the computational requirements,
the sampling rate of the recorded physiological sig-
nals was reduced to 256 Hz. Each physiological chan-
nel was subsequently processed by applying specific
signal processing techniques in order to significantly
reduced the amount of noise and artefacts within the
recorded signals. A low-pass Butterworth filter of or-
der 3 with a cut-off frequency of 0.2 Hz was applied
on the EDA signals. A fourth order bandpass But-
terworth filter with a frequency range of [20, 250] Hz
T
1
T
4
T
2
T
3
T
0
2 sec 4 sec 8 − 12 sec 2 sec 4 sec
4.5 sec
4.5 sec
Figure 3: Signal Segmentation. Experiments are carried out
on windows of length 4.5 sec with a temporal shift of 4 sec
from the elicitations’ onset.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
292

was applied to the EMG signals. Concerning the ECG
signals, a third order bandpass Butterworth filter with
a frequency range of [0.1,250] Hz was first applied,
followed by a piecewise detrending by subtracting a
5
th
degree polynomial least-squares fit from the fil-
tered signals.
The filtered signals were subsequently segmented into
windows of length 4.5 sec with a shift of 4 sec
from the elicitation’s onset, as proposed in (Thiam
et al., 2019) (see Figure 3). Each physiological sig-
nal within this specific window constitutes a 1-D ar-
ray of size 4.5 × 256 = 1152. Therefore, the training
material for the proposed approaches specific to each
single participant consists of a tensor with the dimen-
sionality 100 × 1152 × 1. Moreover, data augmenta-
tion was performed by shifting the 4.5 sec window
of segmentation backward and forward in time with
small shifts of 250 milliseconds (ms) and a maximal
total window shift of 1 sec in each direction, start-
ing from the initial position of the window depicted
in Figure 3. This procedure was performed uniquely
during the training phase of the proposed architec-
tures. The performance of the architecture was tested
on the initial windows.
3.3 Architecture Description
In the current work, the Exponential Linear Unit
(ELU) (Clevert et al., 2016) activation function de-
fined in Equation 9
elu
α
(x) =
(
α(exp(x) − 1) if x < 0
x if x ≥ 0
(9)
Table 1: DDCAE Architecture. The kernel size was empir-
ically set to 3 for the EDA channel and 11 for both EMG
and ECG channels, with an identical stride of 1. The pool-
ing size (resp. upsampling size) was set to 2 with a stride of
2. ELU is used as activation function for both convolutional
and fully connected layers.
Encoder
Layer No. kernels/Units
2×Conv1D-MaxPooling 8
2×Conv1D-MaxPooling 16
2×Conv1D-MaxPooling 32
Flatten −
Fully Connected 256
Decoder
Layer No. kernels/Units
Fully Connected 576
Reshape −
2×Conv1D-UpSampling 32
2×Conv1D-UpSampling 16
2×Conv1D-UpSampling 8
Conv1D 1
is used in both convolutional and fully connected lay-
ers (with α = 1), except for the output layer of the
classifier, where a softmax activation function is ap-
plied. Moreover, a similar DDCAE architecture is
designed for each physiological channel. The only
difference between those architectures is the size of
the convolutional kernel which is empirically set to 3
for the EDA channel, and 11 for both EMG and ECG
channels, with the stride set to 1. The dimensionality
of the resulting latent representation for each channel
is identical (η = 256). The corresponding DDCAE ar-
chitecture is depicted in Table 1 and the architecture
of the classifier is depicted in Table 2.
3.4 Experimental Settings
All architectures are trained using the Adaptive Mo-
ment estimation (Adam) (Kingma and Ba, 2015) opti-
mization algorithm with a fixed learning rate set em-
pirically to 10
−5
. The training process is performed
through a total of 100 epoches with the batch size set
to 100. The activity regularization term of Equation
3 is set as follows: λ = 0.001. The regularization
weights of the loss functions in Equation 5 are set
as follows: α
0
= α
1
= α
2
= 0.2, and α
c
= 0.4. The
weight of the classifier’s loss function is set greater
than the others to focus more on the classification
performance of the whole architecture. The Gaus-
sian noise parameters are empirically set to a stan-
dard deviation of 0.1 and a mean of 0. The imple-
mentation and evaluation of the proposed architec-
tures is done with the libraries Keras (Chollet et al.,
2015), Tensorflow (Abadi et al., 2015) and Scikit-
learn (Pedregosa et al., 2011). The evaluation of
the architectures is performed by applying a Leave-
One-Subject-Out (LOSO) cross-validation evaluation,
which means that a total of 87 experiments is per-
formed during which the data specific to each partic-
ipant is used once to evaluate the performance of the
trained deep model and is never seen during its opti-
mization process.
Table 2: Classifier Architecture. The dropout rate was set
empirically to 0.25. ELU is used as activation function for
the first layer, while a softmax activation function is used for
the last fully connected layer (whereby c depicts the number
of classes of the classification task).
Layer No. kernels/Units
Fully Connected 128
Dropout −
Fully Connected c
Multimodal Deep Denoising Convolutional Autoencoders for Pain Intensity Classification based on Physiological Signals
293

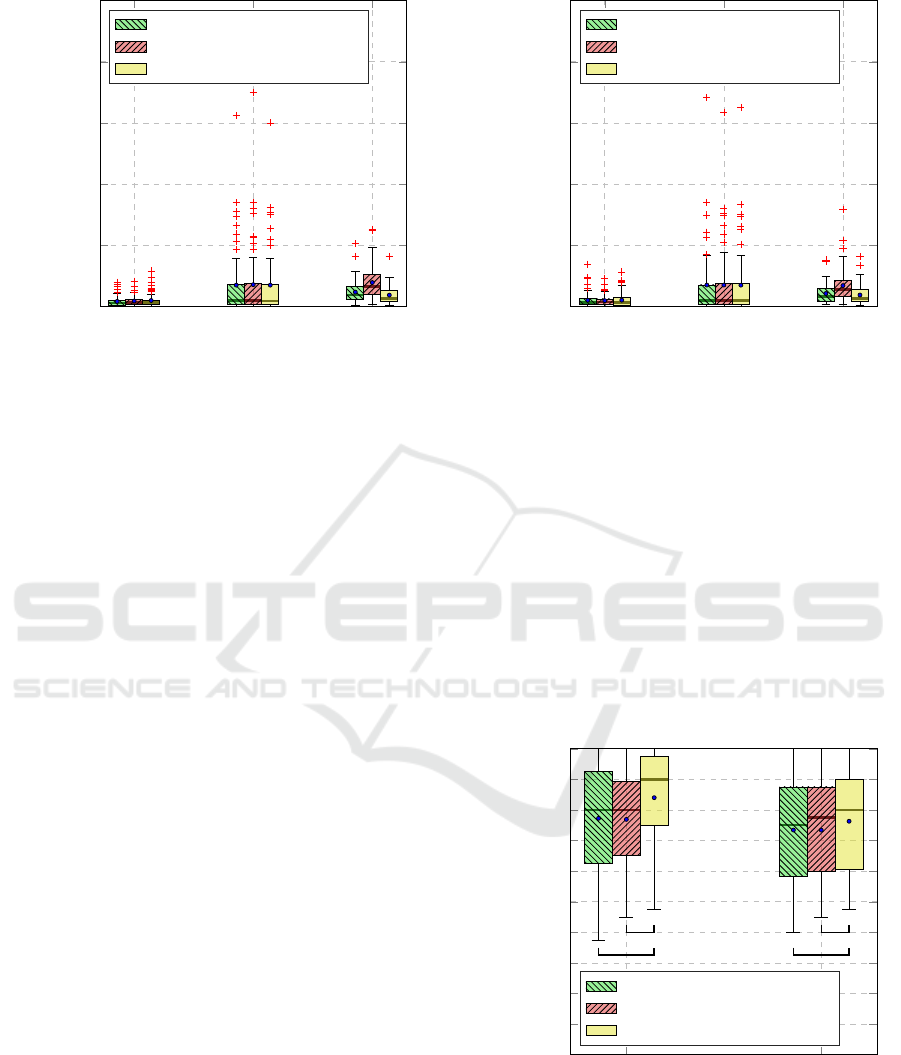
EDA
EMG ECG
0
0.5
1
1.5
2
2.5
T
0
vs.T
4
Mean Squared Error
Concatenated Representation
Shared Representation
Gated Representation
Figure 4: Reconstruction error for the task T
0
vs.T
4
. Within
each boxplot, the mean and median values of the mean
squared errors are depicted with a dot and a horizontal line
respectively.
3.5 Results
The proposed architectures are assessed in two bi-
nary classification tasks: the first one consists of the
discrimination between the baseline temperature (T
0
)
and the pain tolerance temperature (T
4
, which is the
highest level of pain elicitation); the second binary
classification task consists of the discrimination be-
tween the pain threshold temperature (T
1
) and the pain
tolerance temperature (T
4
).
The results specific to the reconstruction error
(Mean Squared Error in this case) of the jointly
trained DDCAEs for each specific architecture and
for each classification task are depicted in Figure 4
and Figure 5 respectively. At a glance, EDA signals
can be accurately reconstructed by all proposed ar-
chitectures, which depict similar reconstruction per-
formances with an average mean squared error in
the range of [0.041, 0.048] for the task T
0
vs.T
4
, and
[0.047, 0.051] for the task T
1
vs.T
4
. Concerning the
EMG channel, the architectures have significantly
more difficulties to reconstruct the signals. This is de-
picted in both Figures 4 and 5 by the huge amount
of outliers with reconstruction errors in the range
[0.5, 2.5]. At last, the reconstruction performances of
the architectures specific to the ECG channel are also
similar. However in this case, the shared latent repre-
sentation architecture performs worst with an average
reconstruction error of 0.19 for the task T
0
vs.T
4
, and
0.17 for the task T
1
vs.T
4
.
Furthermore, the performance of the jointly trained
classifier for each classification task is depicted in
Figure 6. In both cases (T
0
vs.T
4
and T
1
vs.T
4
), the
EDA
EMG ECG
0
0.5
1
1.5
2
2.5
T
1
vs.T
4
Mean Squared Error
Concatenated Representation
Shared Representation
Gated Representation
Figure 5: Reconstruction error for the task T
1
vs.T
4
. Within
each boxplot, the mean and median values of the mean
squared errors are depicted with a dot and a horizontal line
respectively.
gated representation architecture significantly outper-
forms both concatenated and shared representation ar-
chitectures. This proves that using such a gated ap-
proach is not only beneficial for the reduction of the
dimensionality of the final latent representation, but
also, due to the optimized weighting parameters, a
representation that significantly improves the perfor-
mance of the classifier can be generated. Based on
these findings, the performance of the proposed ap-
proaches are compared with those of previous works.
T
0
vs.T
4
T
1
vs.T
4
0
0.2
0.4
0.6
0.8
1
*
*
*
*
Accuracy
Concatenated Representation
Shared Representation
Gated Representation
Figure 6: Classification performance. An asterisk (*) in-
dicates a significant performance improvement between the
gated representation architecture and each of the other ar-
chitectures. The test has been conducted using a Wilcoxon
signed rank test with a significance level of 5%. Within
each boxplot, the mean and the median classification accu-
racy are depicted respectively with a dot and a horizontal
line.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
294

Most of the previous works on this specific dataset are
based on a set of carefully designed hand-crafted fea-
tures. For the sake of fairness, we compare our results
with those results in the literature which are based on
the exact same dataset and were computed based on
the exact same evaluation protocol (LOSO). The re-
sults depicted in Table 3 show that the gated repre-
sentation approach outperforms previous approaches
for the classification task T
0
vs.T
4
.
4 CONCLUSIONS
The previously depicted results prove that training
a single latent representation for each input channel
combined with a gating layer with trainable parame-
ters to generate a weighted latent representation that
is subsequently fed into a jointly trained classifier to
perform a classification task can significantly improve
the classification performance of an entire architec-
ture, while still performing the reconstruction of the
input signals at a satisfactory extent. The proposed ar-
chitecture based on a gated representation also outper-
forms previously proposed classification approaches,
based on a set of carefully designed hand-crafted fea-
tures. This shows that feature learning is also a sound
alternative to manual feature engineering, since the
designed architecture is able to autonomously design
a set of relevant parameters without the need of ex-
pert knowledge in this particular area of application.
Therefore, future works will consist of improving the
architecture of the gating layer and also performing
the fusion of hand-crafted and learned features in or-
der to further improve the performance of the whole
system.
Table 3: Comparison with previous works in a LOSO cross-
validation evaluation for the classification task T
0
vs.T
4
. The
performance metric consists of the average accuracy (in %)
± standard deviation.
Approach Description Performance
Werner et al.
(Werner et al., 2014)
Early Fusion with
Random Forests
(EMG, ECG, EDA)
74.10
Lopez-Martinez et
al. (Lopez-Martinez
and Picard, 2018)
Logistic Regression
(EDA)
74.21 ± 17.54
K
¨
achele et al.
(K
¨
achele et al.,
2016a; K
¨
achele
et al., 2016b)
Early Fusion with
Random Forests
(EMG, ECG, EDA)
82.73
Proposed Approach
Concatenated Latent
Representation
77.24 ± 17.48
Proposed Approach
Shared Latent
Representation
76.90 ± 15.09
Proposed Approach
Gated Latent
Representation
83.99 ± 15.58
ACKNOWLEDGEMENTS
The research leading to these results has received
funding from the Federal Ministry of Education and
Research (BMBF, SenseEmotion) to F.S., (BMBF,
e:Med, CONFIRM, ID 01ZX1708C) to H.A.K.,
and the Ministry of Science and Education Baden-
W
¨
urttemberg (Project ZIV) to H.A.K.. We grate-
fully acknowledge the support of NVIDIA Corpora-
tion with the donation of the Tesla K40 GPU used for
this research.
REFERENCES
Abadi, M., Agarwal, A., Barham, P., Brevdo, E., Chen, Z.,
Citro, C., Corrado, C., Davis, A., Dean, J., Devin, M.,
Ghemawat, S., Goodfellow, I., Harp, A., Irving, G.,
Isard, M., Jia, Y., Jozefowicz, R., Kaiser, L., Kudlur,
M., Levenberg, J., Man
´
e, D., Monga, R., Moore, S.,
Murray, D., Olah, C., Schuster, M., Shlens, J., Steiner,
B., Sutskever, I., Talwar, K., Tucker, P., Vanhoucke,
V., Vasudevan, V., Vi
´
egas, F., Vinyals, O., Warden,
P., Wattenberg, M., Wicke, M., Yu, Y., and Zheng, X.
(2015). Tensorflow: Large-scale machine learning on
heterogeneous systems. https://www.tensorflow.org/.
Software available from tensorflow.org.
Abe, S. (2005). Support Vector Machines for Pattern Clas-
sification. Springer.
Bellmann, P., Thiam, P., and Schwenker, F. (2018). Compu-
tational Intelligence for Pattern Recognition, volume
777, chapter Multi-classifier-Systems: Architectures,
Algorithms and Applications, pages 83–113. Springer
International Publishing, Cham.
Ben Said, A., Mohamed, A., Elfouly, T., Harras, K., and
Wang, Z. J. (2017). Multimodal deep learning ap-
proach for joint eeg-emg data compression and classi-
fication. In IEEE Wireless Communications and Net-
working Conference, pages 1–6.
Breiman, L. (2001). Random forests. Machine Learning,
45(1):5–32.
Chollet, F. et al. (2015). Keras. https://keras.io.
Chu, Y., Zhao, X., Han, J., and Su, Y. (2017). Physiological
signal-based method for measurement of pain inten-
sity. Frontiers in Neuroscience, 11:279.
Clevert, D.-A., Unterthiner, T., and Hochreiter, S. (2016).
Fast and accurate deep neural network learning by ex-
ponential linear units (elus). In Proceedings of the
4th International Conference on Learning Represen-
tations (ICLR).
Ditthapron, A., Banluesombatkul, N., Ketrat, S., Chuang-
suwanich, E., and Wilaiprasitporn, T. (2019). Univer-
sal joint feature extraction for p300 eeg classification
using multi-task autoencoder. IEEE Access, 7:68415–
68428.
Fisher, R. A. (1936). The use of multiple measurement in
taxonomic problems. Annals of Eugenics, 7(2):179–
188.
Multimodal Deep Denoising Convolutional Autoencoders for Pain Intensity Classification based on Physiological Signals
295

Haiyan, W., Haomin, Y., and Xueming, Li abd Haijun, R.
(2015). Semi-supervised autoencoder: A joint ap-
proach of representation and classification. In Interna-
tional Conference on Computational Intelligence and
Communication Networks, pages 1424–1430.
Hinton, G. E. and Salakhutdinov, R. (2006). Reducing the
dimensionality of data with neural networks. Science,
313(5786):504–507.
Hinton, G. E. and Zemel, R. S. (1993). Autoencoders, min-
imum description length and helmholtz free energy.
In Proceedings of the 6th International Conference on
Neural Information Processing Systems, pages 3–10.
K
¨
achele, M., Amirian, M., Thiam, P., Werner, P., Walter, S.,
Palm, G., and Schwenker, F. (2016a). Adaptive confi-
dence learning for the personalization of pain intensity
estimation systems. Evolving Systems, 8(1):1–13.
K
¨
achele, M., Thiam, P., Amirian, M., Schwenker, F.,
and Palm, G. (2016b). Methods for person-
centered continuous pain intensity assessment from
bio-physiological channels. IEEE Journal of Selected
Topics in Signal Processing, 10(5):854–864.
Kessler, V., Thiam, P., Amirian, M., and Schwenker, F.
(2017). Pain recognition with camera photoplethys-
mography. In Seventh International Conference on
Image Processing Theory, Tools and Applications
(IPTA), pages 1–5.
Khattar, D., Goud, J. S., Gupta, M., and Varma, V. (2019).
MVAE: Multimodal Variational Autoencoder for fake
news detection. In The World Wide Web Conference,
pages 2915–2921.
Kingma, D. P. and Ba, J. (2015). Adam: A method for
stochastic optimization. In Proceedings of the 3rd In-
ternational Conference on Learning Representations
(ICLR).
Le, L., Patterson, A., and White, M. (2018). Supervised
autoencoders: Improving generalization performance
with unsupervised regularizers. In Advances in Neural
Information Processing Systems, number 31, pages
107–117. Curran Associates, Inc.
Lim, H., Kim, B., Noh, G.-J., and Yoo, S. K. (2019). A
deep neural network-based pain classifier using a pho-
toplethysmography signal. Sensors, 2(384).
Liu, X., Wang, M., Zha, Z.-J., and Hong, R. (2019a). Cross-
modality feature learning via convolutional autoen-
coder. ACM Transactions on Multimedia Computing,
Communications, and Applications, 15(1s):7:1–7:20.
Liu, X., Zhou, Q., Zhao, J., Shen, H., and Xiong, X.
(2019b). Fault diagnosis of rotating machinery un-
der noisy environment conditions based on a 1-d con-
volutional autoencoder and 1-d convolutional neural
network. Sensors, 19(972).
Lopes, N. and Ribeiro, B. (2015). Machine Learning
for Adaptive Many-Core Machines - A Practical Ap-
proach, chapter Deep Belief Networks (DBNs), pages
155–186. Springer International Publishing.
Lopez-Martinez, D. and Picard, R. (2018). Continuous pain
intensity estimation from autonomic signals with re-
current neural networks. In 40th Annual International
Conference of the IEEE Engineering in Medecine and
Biology Society (EMBC), pages 5624–5627.
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V.,
Thirion, B., Grisel, O., Blondel, M., Prettenhofer,
P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,
A., Cournapeau, D., Brucher, M., Perrot, M., and
Duchesnay, E. (2011). Scikit-learn: Machine learning
in Python. Journal of Machine Learning Research,
12:2825–2830.
Squires, N. K., Squires, K. C., and Hillyard, S. A. (1975).
Two varieties of long-latency positive waves evoked
by unpredictable auditory stimuli in man. Elec-
troencephalography and Clinical Neurophysiology,
38(4):387–401.
Thiam, P., Kessler, V., Amirian, M., Bellmann, P., Layher,
G., Zhang, Y., Velana, M., Gruss, S., Walter, S., Traue,
H. C., Kim, J., Schork, D., Andr
´
e, E., Neumann, H.,
and Schwenker, F. (2019). Multi-modal pain inten-
sity recognition based on the senseemotion database.
IEEE Transactions on Affective Computing, pages 1–
1.
Thiam, P., Meudt, S., Palm, G., and Schwenker, F. (2018). A
temporal dependency based multi-modal active learn-
ing approach for audiovisual event detection. Neural
Processing Letters, 48(2):709–732.
Thiam, P. and Schwenker, F. (2017). Multi-modal data fu-
sion for pain intensity assessement and classification.
In 2017 Seventh International Conference on Image
Processing Theory, Tools and Applications (IPTA),
pages 1–6.
Vukoti
´
c, V., Raymond, C., and Gravier, G. (2016). Bidi-
rectional joint representation learning with symmetri-
cal deep neural networks for multimodal and cross-
modal applications. In Proceedings of the 2016 ACM
on International Conference on Multimedia Retrieval,
pages 343–346.
Walter, S., Gruss, S., Ehleiter, H., Tan, J., Traue, H. C.,
Crawcour, S., Werner, P., Al-Hamadi, A., and An-
drade, A. (2013). The BioVid heat pain database data
for the advancement and systematic validation of an
automated pain recognition system. In IEEE Interna-
tional Conference on Cybernetics, pages 128–131.
Werner, P., Al-Hamadi, A., Niese, R., Walter, S., Gruss, S.,
and Traue, H. C. (2014). Automatic pain recognition
from video and biomedical signals. In Proceedings of
the International Conference on Pattern Recognition
(ICPR), pages 4582–4587.
Yang, X., Ramesh, P., Chitta, R., Madhvanath, S., Bernal,
E. A., and Luo, J. (2017). Deep multimodal repre-
sentation learning from temporal data. In IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 5447–5455.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
296