
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid
Domains by Leveraging Knowledge Compilation
Anton R. Fuxjaeger
1
and Vaishak Belle
1,2
1
University of Edinburgh, U.K.
2
Alan Turing Institute, U.K.
Keywords:
Weighted Model Integration, Probabilistic Inference, Knowledge Compilation, Sentential Decision Diagrams,
Satisfiability Modulo Theories.
Abstract:
Weighted model integration (WMI) extends weighted model counting (WMC) in providing a computational
abstraction for probabilistic inference in mixed discrete-continuous domains. WMC has emerged as an as-
sembly language for state-of-the-art reasoning in Bayesian networks, factor graphs, probabilistic programs
and probabilistic databases. In this regard, WMI shows immense promise to be much more widely applicable,
especially as many real-world applications involve attribute and feature spaces that are continuous and mixed.
Nonetheless, state-of-the-art tools for WMI are limited and less mature than their propositional counterparts.
In this work, we propose a new implementation regime that leverages propositional knowledge compilation for
scaling up inference. In particular, we use sentential decision diagrams, a tractable representation of Boolean
functions, as the underlying model counting and model enumeration scheme. Our regime performs compet-
itively to state-of-the-art WMI systems but is also shown to handle a specific class of non-linear constraints
over non-linear potentials.
1 INTRODUCTION
Weighted model counting (WMC) is a basic reason-
ing task on propositional knowledge bases. It ex-
tends the model counting task, or #SAT, which is
to count the number of satisfying assignments to a
given propositional formula (Biere et al., 2009). In
WMC, one accords a weight to every model and com-
putes the sum of the weights of all models. The
weight of a model is often factorized into weights
of assignments to individual variables. WMC has
emerged as an assembly language for numerous for-
malisms, providing state-of-the-art probabilistic rea-
soning for Bayesian networks (Chavira and Dar-
wiche, 2008), factor graphs (Choi et al., 2013),
probabilistic programs (Fierens et al., 2015), and
probabilistic databases (Suciu et al., 2011). Ex-
act WMC solvers are based on knowledge compi-
lation (Darwiche, 2004; Muise et al., 2012) or ex-
haustive DPLL search (Sang et al., 2005). These
successes have been primarily enabled by the devel-
opment of efficient data structures, e.g., arithmetic
circuits (ACs), for representing Boolean theories, to-
gether with fast model enumeration strategies. In par-
ticular, the development of ACs has enabled a number
of developments beyond inference, such as parame-
ter and structure learning (Bekker et al., 2015; Liang
et al., 2017; Poon and Domingos, 2011; Kisa et al.,
2014; Poon and Domingos, 2011). Finally, having
a data structure in hand means that multiple queries
can be evaluated efficiently: that is, exhaustive search
need not be re-run for each query.
However, WMC is limited to discrete finite-
outcome distributions only, and little was understood
about whether a suitable extension exists for contin-
uous and discrete-continuous random variables until
recently. The framework of weighted model integra-
tion (WMI) (Belle et al., 2015) extended the usual
WMC setting by allowing real-valued variables over
symbolic weight functions, as opposed to purely nu-
meric weights in WMC. The key idea is to use formu-
las involving real-valued variables to define a hyper-
rectangle or a hyper-rhombus, or in general, any arbi-
trary region of the event space of a continuous ran-
dom variable, and use the symbolic weights to de-
fine the corresponding density function for that re-
gion.WMC is based on propositional SAT technol-
ogy and, by extension, WMI is based on satisfiability
modulo theories (SMT), which enable us to, for ex-
ample, reason about the satisfiability of linear con-
Fuxjaeger, A. and Belle, V.
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid Domains by Leveraging Knowledge Compilation.
DOI: 10.5220/0008896003470355
In Proceedings of the 12th International Conference on Agents and Artificial Intelligence (ICAART 2020) - Volume 2, pages 347-355
ISBN: 978-989-758-395-7; ISSN: 2184-433X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
347

straints over the reals (Barrett et al., 2009). Thus,
for every assignment to the Boolean and continuous
variables, the WMI problem defines a density. The
WMI for a knowledge base (KB) ∆ is computed by
integrating these densities over the domain of so-
lutions to ∆, which is a mixed discrete-continuous
space, yielding the value for a probabilistic query.
The approach is closely related to the mixture-of-
polynomials density estimation for hybrid Bayesian
networks (Shenoy and West, 2011). Applications
of WMI (and closely related formulations) for prob-
abilistic graphical modelling and probabilistic pro-
gramming tasks have also been emerging (Chistikov
et al., 2017; Albarghouthi et al., 2017; Morettin et al.,
2017).
Given the popularity of WMC, WMI shows im-
mense promise to be much more widely applicable,
especially as many real-world applications, includ-
ing time-series models, involve attribute and feature
spaces that are continuous and mixed. However, state-
of-the-art tools for WMI are limited and significantly
less mature than their propositional counterparts. Ini-
tial developments on WMI (Belle et al., 2015) were
based on the so-called block-clause strategy, which
naively enumerates the models of a LR A (linear real
arithmetic) theory and is impractical on all but small
problems. Recently, a solver based on predicate ab-
straction was introduced by (Morettin et al., 2017)
with strong performance, but since no explicit circuit
is constructed, it is not clear how tasks like parameter
learning can be realized. Following that development,
(Kolb et al., 2018) proposed the use of extended alge-
braic decision diagrams (Sanner et al., 2012), an ex-
tension of algebraic decision diagrams (Bahar et al.,
1997), as a compilation language for WMI. They also
perform comparably to (Morettin et al., 2017).
However, while this progress is noteworthy, there
are still many significant differences to the body of
work on propositional circuit languages. For exam-
ple, properties such as canonicity have received con-
siderable attention for these latter languages (Van den
Broeck and Darwiche, 2015). Many of these lan-
guages allow (weighted) model counting to be com-
puted in time linear in the size of the obtained circuit.
To take advantage of these results, in this work we re-
visit the problem of how to leverage propositional cir-
cuit languages for WMI more carefully and develop a
generic implementation regime to that end. In partic-
ular, we leverage sentential decision diagrams (SDDs)
(Darwiche, 2011) via abstraction. SDDs are tractable
circuit representations that are at least as succinct
as ordered binary decision diagrams (OBDDs) (Dar-
wiche, 2011). Both of these support querying such as
model counting (MC) and model enumeration (ME)
in time linear in the size of the obtained circuit. (We
use the term querying to mean both probabilistic con-
ditional queries as well as weighted model count-
ing because the latter simply corresponds to the case
where the query is true.) Because of SDDs having
such desirable properties, several papers have dealt
with more involved issues, such as learning the struc-
ture from data directly (Bekker et al., 2015; Liang
et al., 2017) and thus learning the structure of the un-
derlying graphical model.
In essence, our implementation regime uses SDDs
as the underlying querying language for WMI in or-
der to perform tractable and scalable probabilistic in-
ference in hybrid domains. The regime neatly sep-
arates the model enumeration from the integration,
which is demonstrated by allowing a choice of two
integration schemes. The first is a provably efficient
and exact integration approach for polynomial den-
sities (De Loera et al., 2004; Baldoni et al., 2011;
De Loera et al., 2011) and the second is an unmodi-
fied integration library available in the programming
language platform (Python in our case). The results
obtained are very promising with regards to the em-
pirical behaviour: we perform competitively to the
existing state-of-the-art WMI solver (Morettin et al.,
2017). But perhaps most significantly, owing to the
generic nature of our regime, we can scale the same
approach to non-linear constraints, with possibly non-
linear potentials.
2 BACKGROUND
Probabilistic Graphical Models. Throughout this
paper we will refer to Boolean and continuous ran-
dom variables as B
j
and X
i
respectively for some fi-
nite j > 0,i > 0. Lower case letters, b
j
∈ {0,1} and
x
i
∈ R, will represent the instantiations of these vari-
ables. Bold upper case letters will denote sets of vari-
ables and bold lower case letters will denote their
instantiations. We are broadly interested in proba-
bilistic models, defined on B and X. That is, let
(b,x) = (b
1
,b
2
,. .. ,b
m
,x
1
,x
2
,. .. ,x
n
) be one element
in the probability space {0,1}
m
∗ R
n
, denoting a par-
ticular assignment to the values in the respective do-
mains. A graphical model can then be used to de-
scribe dependencies between the variables and define
a joint density function of those variables compactly.
The graphical model we will consider in this paper
are Markov networks, which are undirected models.
(Directed models can be considered too (Chavira and
Darwiche, 2008), but are ignored for the sake of sim-
plicity.)
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
348

Logical Background. Propositional satisfiability
(SAT) is the of determining if a given formula in
propositional logic can be satisfied by an assignment
(, where a satisfying assignment has to be provided
as proof for a formula being satisfiable). An instance
of satisfiability modulo theory (SMT) (Biere et al.,
2009) is a generalization of classical SAT in allow-
ing first-order formulas with respect to some decid-
able background theory. For example, LR A is under-
stood here as quantifier-free linear arithmetic formu-
las over the reals and the corresponding background
theory is the fragment of first-order logic over the
signature (0,1,+,≤), restricting the interpretation of
these symbols to standard arithmetic.
In this work, we will consider two different back-
ground theories: quantifier-free linear (LR A) and
non-linear (N R A) arithmetic over the reals. A prob-
lem instance (input) to our WMI solver is then a for-
mula with respect to one of those background theories
in combination with propositional logic for which sat-
isfaction is defined in an obvious way (Barrett et al.,
2009). Such an instance is referred to as a hybrid
knowledge base (HKB).
Weighted Model Counting. Weighed model
counting (WMC) (Chavira and Darwiche, 2008) is a
strict generalization of model counting (Biere et al.,
2009). In WMC, each model of a given propositional
knowledge base (PKB) Γ has an associated weight
and we are interested in computing the sum of
the weights that correspond to models that satisfy
Γ. (As is convention, the underlying propositional
language and propositional letters are left implicit.
We often refer to the set of literals L to mean the set
of all propositional atoms as well as their negations
constructed from the propositions mentioned in Γ.)
In order to create an instance of the WMC prob-
lem given a PKB Γ and literals L, we define a weight
function wf : L → R
≥0
mapping the literals to non-
negative, numeric weights. We can then use the lit-
erals of a given model m to define the weight of that
model as well as the weighted model count as follows:
Definition 1. Given a PKB Γ over literals L (con-
structed from Boolean variables B) and weight func-
tion wf : L → R
≥0
, we define the weight of a model
as:
WEIGHT(m,wf ) =
∏
l∈m
wf (l) (1)
Further we define the weighted model count (WMC)
as:
WMC(Γ,wf ) =
∑
m|=Γ
WEIGHT(m,wf ) (2)
It can be shown that WMC can be used to cal-
culate probabilities of a given graphical model N
by means of a suitable encoding (Chavira and Dar-
wiche, 2008). In particular, conditional probabilities
can be calculated using: Pr
N
(q|e) =
WMC(Γ∧q∧e,wf )
WMC(Γ∧e,wf )
for some evidence e and query q, where e,q are PKBs
as well, defined from B.
Weighted Model Integration. While WMC is very
powerful as an inference tool, it suffers from the in-
herent limitation of only admitting inference in dis-
crete probability distributions. This is due to its un-
derlying theory in enumerating all models (or expand-
ing the complete network polynomial), which is ex-
ponential in the number of variables, but still finite
and countable in the discrete case. For the continuous
case, we need to find a language to reason about the
uncountable event spaces, as well as represent density
functions. WMI (Belle et al., 2015) was proposed as
a strict generalization of WMC for hybrid domains,
with the idea of annotating a SMT theory with poly-
nomial weights.
Definition 2. (Belle et al., 2015) Suppose ∆ is a HKB
over Boolean and real variables B and X, and literals
L. Suppose wf : L → EXPR(X), where EXPR(X) are
expressions over X. Then we define WMI as:
WMI(∆,wf ) =
∑
m|=∆
−
VOL(m,wf ) (3)
where:
VOL(m,wf ) =
Z
{l
+
:l∈m}
WEIGHT(m,wf )dX (4)
and WEIGHT is defined as described in Def 1.
Intuitively the WMI of an SMT theory ∆ is de-
fined in terms of the models of its propositional ab-
straction ∆
−
. For each such model we compute its
volume, that is, we integrate the WEIGHT-values of
the literals that are true in the model. The interval of
the integral is defined in terms of the refinement of the
literals. The weight function wf is to be seen as map-
ping an expression e to its density function, which is
usually another expression mentioning the variables
appearing in e. Conditional probabilities can be cal-
culated as before.
Sentential Decision Diagram. Sentential decision
diagrams (SDDs) were first introduced in (Darwiche,
2011) and are graphical representations of propo-
sitional knowledge bases. SDDs are shown to be
a strict subset of deterministic decomposable nega-
tion normal form (d-DNNF), a popular representation
for probabilistic reasoning applications (Chavira and
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid Domains by Leveraging Knowledge Compilation
349
Darwiche, 2008) due to their desirable properties. De-
composability and determinism ensure tractable prob-
abilistic (and logical) inference, as they enable MAP
queries in Markov networks. SDDs however satisfy
two even stronger properties found in ordered binary
decision diagrams (OBDD), namely structured de-
composability and strong determinism. Indeed, (Dar-
wiche, 2011) showed that they are strict supersets
of OBDDs as well, inheriting their key properties:
canonicity and a polynomial time support for Boolean
combination. Finally SDD’s also come with an upper
bound on their size in terms of tree-width. In the in-
terest of space, we will not be able to discuss SDD
properties in detail. However, we refer the reader to
the original paper (Darwiche, 2011) for an in-depth
study of SDDs and the central results of SDDs that
we appeal to.
3 METHOD
Over the past few years there have been several papers
on exact probabilistic inference (Morettin et al., 2017;
Sanner et al., 2012; Kolb et al., 2018) using the for-
mulation of WMI. What we propose in this section is
a novel formulation of doing weighted model integra-
tion by using SDDs as the underlying model counting,
enumeration and querying language. Here predicate
abstraction and knowledge compilation enable us to
compile the abstracted PKB into an SDD, which has
the desirable property of a fully parallelisable poly-
time model-enumeration algorithm. Recall that poly-
time here refers to the complexity of the algorithm
with respect to the size of the tree (SDD) (Darwiche
and Marquis, 2002).
In practice, computing the probability of a given
query for some evidence consists of calculating the
WMI of two separate but related HKBs. That is, we
have to compute the WMI of a given HKB ∆ con-
joined with some evidence e and the query q, divid-
ing it by the WMI of ∆ conjoined with the evidence
e. This formulation introduced by (Belle et al., 2015)
and explained in more detail in Section 2, can be writ-
ten as:
Pr
∆
(q|e) =
WMI(∆ ∧ e ∧ q)
WMI(∆ ∧ e)
(5)
We will give a quick overview of the whole
pipeline for computing the WMI value of a given
KB, before discussing in detail the individual com-
putational steps.
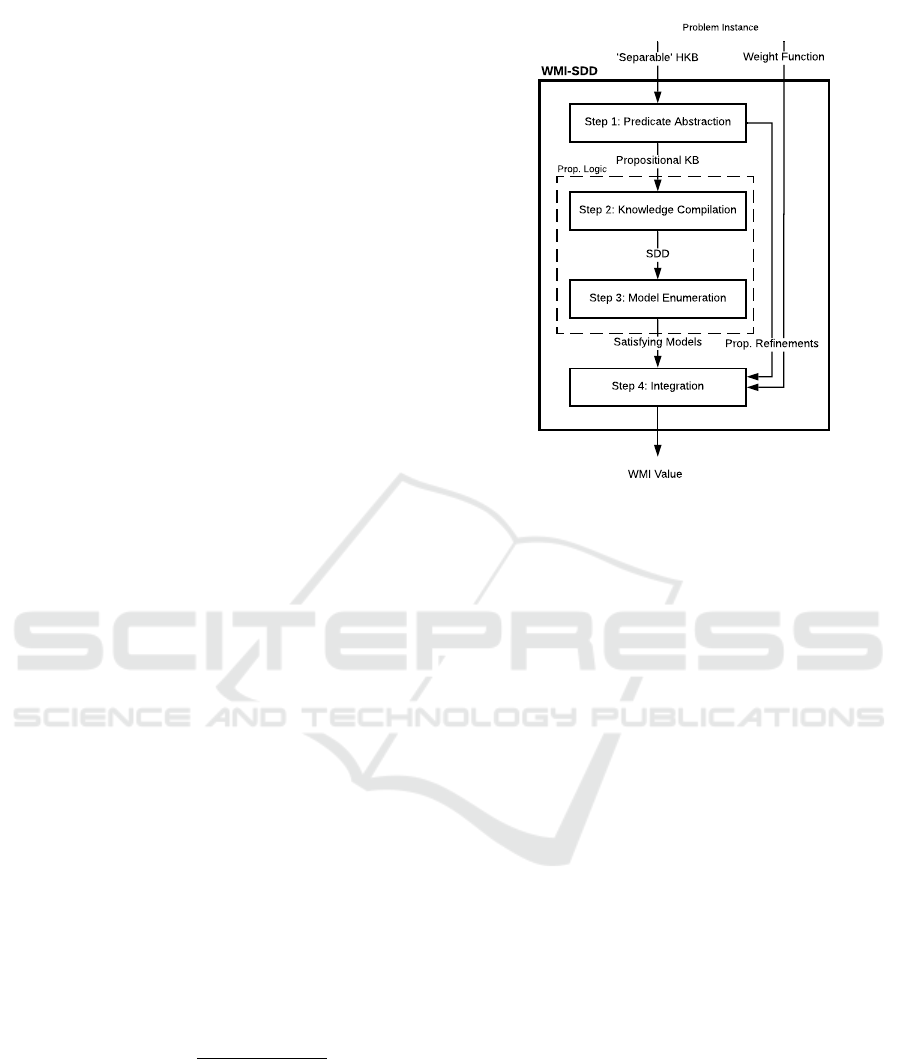
Step 1: Predicate Abstraction
Step 2: Knowledge Compilation
Step 3: Model Enumeration
Step 4: Integration
'Separable' HKB
Propositional KB
SDD
Satisfying Models
Weight Function
Prop. Refinements
Problem Instance
Prop. Logic
WMI Value
WMI-SDD
Figure 1: Pictorial depiction of the proposed pipeline for
WMI.
3.1 WMI-SDD: The Pipeline
As a basis for performing probabilistic inference, we
first have to be able to calculate the WMI of a given
HKB ∆ with corresponding weight function wf . As
we are interested in doing so by using SDDs as a
query language, the WMI breaks down into a se-
quence of sub-computations depicted as the WMI-
SDD pipeline in Figure 1.
Input/Outputs of the Pipeline. The input of the
pipeline is composed of two things: the HKB with re-
spect to some background theory (eg. LR A,N R A)
on the one hand and the weight function on the other.
Here, atoms are defined as usual for the respective
language (Barrett et al., 2009) and can be under-
stood as functions that cannot be broken down fur-
ther into a conjunction, disjunction or negation of
smaller expressions. This means that a HKB of the
form ((X
1
< 3) ∧ (X
1
> 1)) should be abstracted as
(B
1
∧ B
2
) with B
+
1
= (X
1
< 3) and B
+
2
= (X
1
> 1),
rather than B
0
with B
+
0
= (X
1
< 3) ∧ (X
1
> 1).
The first step is to arrange atoms in a form that
we call ‘separable’. The corresponding background
theory determines whether a correct rewriting of for-
mulas is possible to satisfy this condition:
Definition 3. A given HKB ∆ satisfies the condi-
tion separable if every atom within the formula can
be rewritten in one of the following forms: X
1
<
d(A), d(A) < X
1
, X
1
≤ d(A), d(A) ≤ X
1
or d(A) ≤
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
350

X
1
∧ X
1
≤ d(A) where d(A) is any term over A ⊆
VARS − {X
1
}, with VARS being the set of all vari-
ables (Boolean and continuous) that appear in the
atom. That is, by construction, X
1
/∈ A for any given
variable X
1
∈ VARS. Such a variable X
1
is then called
the leading variable (leadVar).
For some background theories, this conversion is
immediate. In a LR A formula ∆
LR A
, any given atom
can be rewritten as an inequality or equality where we
have a single variable on one side and a linear function
on the other side, such as (X
1
< 3 + X
2
). But this is
not a given for HKBs with background theory N R A.
For example, (3 < 2 ∗ X
1
+ X
2
2
) can be rewritten as
(X
1
< 3/2 − 1/2 ∗ X
2
2
) for X
1
and therefore satisfies
the condition. However, the atom (3 < X
4
1
− 3 ∗ X
2
1
)
cannot be rewritten in a similar manner and thus does
not satisfy the condition.
Considering the motivation of performing proba-
bilistic inference, where we deal with evidence and
queries in addition to an HKBs, as discussed in Sec-
tion 2, we note that all elements of {∆,q,e} have to
fulfil the separability condition. As queries and ev-
idence are applied by means of a logical connective
with the HKB, they should generally be thought of as
HKBs themselves.
The weight function wf , on the other hand,
is only restricted by the condition that the term
WEIGHT(m,wf ) must be integratable for any given
model m. As long as this condition is met, we
can accept any arbitrary function over the variables
(Boolean and continuous) of the KB.
3.2 Step 1: Predicate Abstraction
The aim of this step in the WMI framework is
twofold. On the one hand, it is given an HKB (∆) and
is tasked to produce a PKB (∆
−
) and the correspond-
ing mapping from propositional variables to contin-
uous refinements, utilizing propositional abstraction.
On the other hand, this part of the framework also re-
arranges the continuous refinements such that a single
variable is separated from the rest of the equation to
one side of the inequality/equality.
On a conceptual level, the predicate abstraction
closely follows the theoretical formulation introduced
in (Belle et al., 2015). The HKB is recursively tra-
versed and every encountered atom is replaced with
a propositional variable, while the logical structure
(connectives and parentheses) of the KB is preserved.
We make use of the imposed separable property
to rewrite the individual refinements into bounds for
a given variable. These bounds can easily be negated
and will be used at a later stage to construct the inter-
vals of integration for a given model. Now the pro-
cess of rewriting a single atom corresponds to sym-
bolically solving an equation for one variable and it is
implemented as an arithmetic solver. The variable we
choose to isolate from the rest of the equation (that is,
the leading variable), is determined by a variable or-
der, that in turn enforces the order of integration in a
later stage of the pipeline. For example, assume that
the chosen variable order is the usual alphabetical one
over the variable names. Then predicates are rewrit-
ten such that from all variables referenced in the atom,
the one highest up in the variable order is chosen as
the leading variable and separated from the rest of the
equation, resulting in a bound for the given variable.
This ensures that for any predicate the bound for the
leading variable does not reference any variable that
precedes it alphabetically, which in turn ensures that
the integral to be computed is defined and will result
in natural number representing the volume.
Example 1. To illustrate this with an example, con-
sider the HKB ∆: ∆ = (B
0
∧ (X
1
< 3) ∧ (0 < X
1
+
X
2
)) ∨ (X
2
< 3 ∧ X
2
> 0). After abstraction we are
given the PKB ∆
−
= (B
0
∧B
1
∧B
2
)∨ (B
3
∧B
4
) where
the abstracted variables correspond to the follow-
ing atoms: B
+
1
= (X
1
< 3), B
+
2
= (0 < X
1
+ X
2
),
B
+
3
= (X
2
< 3) and B
+
4
= (X
2
> 0). As mentioned
above, we construct the order of the continuous vari-
able alphabetically, resulting in {1 : X
1
,2 : X
2
} for
the proposed example. Once the order has been con-
structed we can rewrite each predicate as a bound
for the variable appearing first in the order: B
1
=
(X
1
< 3), B
2
= (−1 ∗ X
2
< X
1
), B
3
= (X
2
< 3)
and B
4
= (0 < X
2
). This ensures that the integral
R R
wf (X
1
,X
2
)dX
1
dX
2
computes a number for every
possible model of the KB. Considering for example
the model [B
0
,B
1
,B
2
,B
3
,B
4
], the bounds of the inte-
gral would be as follows:
R
3
0
R
3
−X
2
wf (X
1
,X
2
)dX
1
dX
2
and yields a number.
In the case of non-linear refinements, the step of
rearranging the variable could give rise to new propo-
sitions, that in turn have to be added to the PKB.
Consider, for example that the predicate B with the
refinement: B
+
= (4 < X
1
∗ X
2
) should be rewrit-
ten for the variable X
1
as the leading one. Now as
the variable X
2
might be negative or zero, we are
unable to simply divide both sides by X
2
but rather
have to split up the equation in the following way:
B
+
new
= (((X
2
> 0) → (4/X
2
< X
1
)) ∧ ((X
2
< 0) →
(4/X
2
> X
1
)) ∧ ((X
2
= 0) → False)) which can be
further abstracted as: B
+
new
= ((B
1
→ B
2
) ∧ (B
3
→
B
4
)∧((¬B
1
∧¬B
3
) → False)). Once created, we can
replace B with its Boolean function refinement in the
PKB and add all the new predicates (B
1
,B
2
,B
3
,B
4
) to
our list of propositions.
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid Domains by Leveraging Knowledge Compilation
351

3.3 Step 2: Knowledge Compilation
In this step of our pipeline, the PKB constructed in
the previous step is compiled into a canonical SDD. In
practice, we first convert the PKB to CNF before pass-
ing it to the SDD library.
1
The library has a number of
optimizations in place, including dynamic minimiza-
tion (Choi and Darwiche, 2013). However, the algo-
rithm is still constrained by the asymptotically expo-
nential nature of the problem. In addition, it requires
the given PKB to be in CNF or DNF format. Once
the SDD is created, it is imported back into our inter-
nal data structure, which is designed for retrieving all
satisfying models of a given SDD.
3.4 Step 3: Model Enumeration
Retrieving all satisfying models of a given PKB is
a crucial part of the WMI formulation and we now
focus on this step in our pipeline. In essence, we
make use of knowledge compilation to compile the
given PKB into a data structure, which allows us to
enumerate all satisfying models in polynomial time
with respect to the size of the tree. As discussed in
the background section, SDDs are our data structures
of choice and their properties, including canonicity,
make them an appealing choice for our pipeline.
The algorithm we developed for retrieving the sat-
isfying models makes full use of the structural prop-
erties of SDDs. By recursively traversing the tree
bottom-up, models are created for each node in the
SDD with respect to the vtree node it represents.
Those models are then passed upwards in the tree
where they are combined with other branches. This is
possible due to the structured decomposability prop-
erty of the SDD data structure. It should also be noted
at this point that parallelisation of the algorithm is
possible as well due to SDDs decomposability proper-
ties. This is a highly desirable attribute when it comes
to scaling to very large theories.
3.5 Step 4: Integration
The workload of this part of the framework is to com-
pute the volume (VOL) (as introduced in Def 2) for
every satisfying model that was found in the previ-
ous step. That volume for a given model of the PKB
is computed by integrating the weight function (wf )
over the literals true at the model, where the bound of
the integral corresponds to the refinement and truth
value of a given propositional variable within the
model. All such volumes are then summed together
and give the WMI value of the given HKB.
1
http://reasoning.cs.ucla.edu/sdd/
Computing a volume for a given model consists of
two parts: firstly we have to combine the refinements
of predicates appropriately, creating the bounds of in-
tegration before actually integrating over the wf with
respect to the variables and bounds. As discussed in
the predicate abstraction and rewriting step, a given
predicate (that has a refinement) consists of a leading
variable and a bound for the variable. Combining the
bounds into an interval is explained in Algorithm 1.
Algorithm 1 : Combining the intervals for a leadVar and
model.
1: procedure COMBINE(leadVar, predicates, model)
2: interval ← (-inf,inf)
3: for pred in predicates do
4: if pred.leadVar 6= leadVar then
5: continue
6: if model[pred.idx] == false then
7: newBound = negate(pred.bound)
8: else
9: newBound = pred.bound
10: interval = combine(interval,newBound)
11: return interval
Here the function combine combines
intervals via intersections. For exam-
ple, combine((-inf,inf), (-inf,X
1
< 3)) =
(-inf,min(inf, 3)) = (-inf,3) and combine((X
2
+
X
3
,inf), (X
2
/3∗ X
2
< X
1
,inf)) = (max(X
2
+X
3
,X
3
/3∗
X
2
),inf). This procedure is done for every variable
referenced in wf , ensuring that we have a bound of
integration for every such variable.
Naturally, not all abstracted models have to be
models of the original SMT theory. For example,
suppose that a model makes both X
0
< 5 and X
0
>
10 true, abstracted as B
1
and B
2
, then the proposi-
tional abstraction erroneously retrieves a model where
[B
1
,B
2
,. ..], and so the interval bounds would be
(10 < X
0
< 5). Clearly, then, the model should not be
considered as a model for the SMT theory and is sim-
ply disregarded. Once all the real bounds of integra-
tion are defined for the given model, the next step be-
fore integrating is to enumerate all possible instantia-
tions of Boolean variables referenced in the wf . The
different integration problems are then hashed such
that the system only has to compute the integration
once, even if they appear multiple times.
When it comes to the implementation of this part
of the framework, we used two different integration
methods. We support the integration module of the
scipy python package
2
to compute the defined inte-
gral for a given wf , a set of intervals and the instan-
tiations of Boolean variables. Using this package al-
lowed us to formalize the method as described above
and perform inference in non-linear domains. How-
2
https://scipy.org/
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
352
ever, this formulation is not exact and suffers from a
slow runtime. For this reason, we also implemented
the pipeline using latte,
3
an exact integration software
that is particularly well-suited for piecewise polyno-
mial density approximations.
4 EMPIRICAL EVALUATION
Here, we evaluate the proposed framework on the
time it needs to compute the WMI of a given HKB
and wf . It is a proof-of-concept system for WMI via
SDDs. To evaluate the framework, we randomly gen-
erate problems, as described below and compare the
time to the WMI-PA framework developed in (Moret-
tin et al., 2017).
4
4.1 Problem Set Generator
A problem is generated based on 3 factors: the num-
ber of variables, the number of clauses and the per-
centage of real variables.
When generating a new Boolean atom, we simply
return a Boolean variable with the given ID, whereas
generating a real-valued atom is more intricate and
depends on the kind of HKB we are generating (i.e.,
LR A vs N R A). For both background theories we
generate a constant interval for a given variable ID
with probability 0.5 (e.g., 345 < X
3
< 789 for vari-
able ID 3). Otherwise, we pick two random subsets
of all other real variables X
L
,X
U
⊂ VARS
Real
for the
upper and lower bound respectively. Now if we are
generating an HKB with respect to the background
theory LR A, we sum all variables in the upper as
well as the lower bound, to create a linear function
as the upper and lower bound for the variable. Sim-
ilarly, when generating an HKB with respect to the
background theory N R A, we conjoin the variables
of a given set (X
L
,X
U
) by multiplication rather than
by addition. Finally, when creating such an interval
we additionally add a constant interval for the same
variable ID to make sure our integration is definite
and evaluates to a real number.
In order to evaluate our framework, we let the
number of variables (nbVars) range from 2 to 28,
where the number of clauses we tested is nbVars∗0.7,
nbVars and nbVars ∗ 1.5 for a given value of nbVars.
3
https://www.math.ucdavis.edu/
∼
latte/
4
We were unable to compare the performance with the
framework developed in (Kolb et al., 2018) owing to com-
patibility issues in the experimental setup. Since it is re-
ported to perform comparably to (Morettin et al., 2017),
all comparisons made in this paper are in reference to the
pipeline developed in (Morettin et al., 2017).
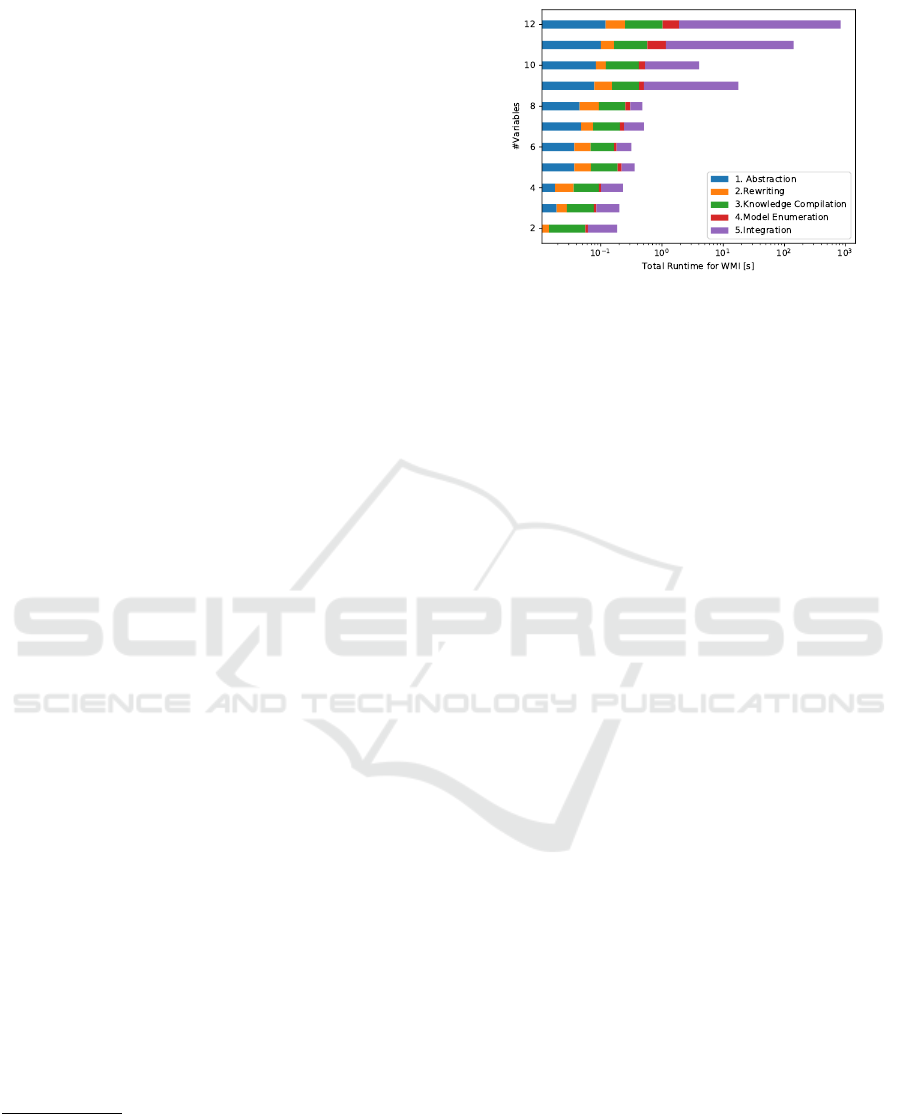
Figure 2: Runtime analysis of WMI-SDD framework for
non-linear HKBs.
Now for each variable clause pair, we generate two
problem instances where the percentage of continu-
ous variables is set to 50% to account for the random-
ness of the generator. Thus for each number of vari-
ables, we generate six different problems, which are
then averaged to compute a final runtime.
5 RESULTS
First, we discuss the performance of our framework
on non-linear hybrid domains. As part of this experi-
ment the generated HKB consists of non-linear atoms
which are products of variables (e.g. X
1
∗ X
2
∗ −4 ∗
X
3
< X
4
< X
1
∗ 27 ∗ X
5
). Figure 2 plots the average
time spent in each computational step for all prob-
lems that have the same number of variables. Here we
see that the overall time increases with the number of
variables as expected. While most of the steps have a
rather small impact on the overall computational time,
the integration step has by far the greatest cost. This
is in part due to the Scipy integration method, which
was used for these benchmarks, as it can cope with
non-linear bounds but is not as efficient as the latte
integration package. Finally, we want to point out the
surprisingly small cost of compiling the PKB into an
SDD, which reinforces our decision to use knowledge
compilation.
Next, we discuss the performance of the WMI-
SDD framework on linear HKBs against one of the
current state-of-the-art WMI solver, the WMI-PA
framework (Morettin et al., 2017). The results are
plotted in Figure 3. The results demonstrate the over-
all impact of using knowledge compilation as part of
the framework. While the additional step of compil-
ing the abstracted PKB into an SDD results in longer
computational time for small problem instances, the
trade-off shows its advantage as we increase the num-
ber of variables. Considering the logarithmic scale of
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid Domains by Leveraging Knowledge Compilation
353
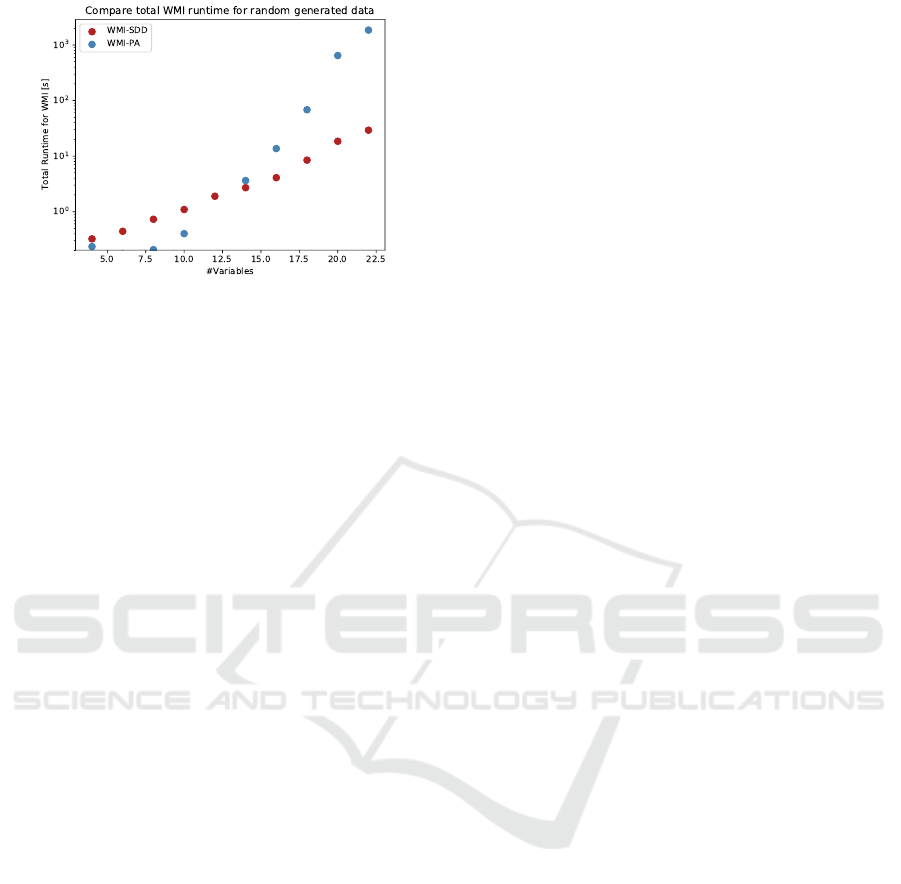
Figure 3: Total runtime comparison WMI-SDD vs WMI-
PA for linear HKBs.
the y-axis, the difference between the two algorithms
becomes quite substantial as the number of variables
exceeds 20. By extension, we believe the WMI-
SDD framework shows tremendous promise for scal-
ing WMI to large domains in the future.
Before concluding this section, we remark that
readers familiar with propositional model counters
are likely to be surprised by the total variable size
being less than 50 in our experiments and other
WMI solvers (Morettin et al., 2017). Contrast this
with SDD evaluations that scale to hundreds of propo-
sitional variables (Darwiche, 2011; Choi and Dar-
wiche, 2013). The main bottleneck here is symbolic
integration, even if in isolation solvers such as latte
come with strong polynomial time bounds (Baldoni
et al., 2011). This is because integration has been per-
formed for each model, and so with n variables and
a knowledge base of the form (a
1
< X
1
< b
1
) ∨ ... ∨
(a
n
< X
n
< b
n
), where a
i
,b
j
∈ R, there are 2
n
∗n inte-
gration computations in the worst case. That is, there
are 2
n
models on abstraction, and in each model, we
will have n integration variables.
There are a number of possible ways to address
that concern. First, a general solution is to simply fo-
cus on piecewise constant potentials, in which case,
after abstraction, WMI over an HKB immediately re-
duces to a WMC task over the corresponding PKB.
Second, parallelisation can be enabled. For example,
we can decompose a CNF formula into components,
which are CNF formulas themselves, the idea being
that components do not share variables (Gomes et al.,
2009). In this case, the model count of a formula F,
written #F with n components C
1
,. .. ,C
n
would be
#C
1
∗ · ·· ∗ #C
n
. This is explored for the interval frag-
ment in (Belle et al., 2016). Third, one can keep a dic-
tionary of partial computations of the integration (that
is, cache the computed integrals), and apply these val-
ues where applicable.
While we do not explore such possibilities in this
article, we feel the ability of SDDs to scale as well as
its ability to enable parallelisation can be seen as addi-
tional justifications for our approach. We also suspect
that it should be fairly straightforward to implement
such choices given the modular way our solver is re-
alized.
6 CONCLUSION
In this paper, we introduced a novel way of perform-
ing WMI by leveraging efficient predicate abstrac-
tion and knowledge compilation. Using SDDs to rep-
resent the abstracted HKBs enabled us to make full
use of the structural properties of SDD and devise an
efficient algorithm for retrieving all satisfying mod-
els. The evaluations demonstrate the competitiveness
of our framework and reinforce our hypothesis that
knowledge compilation is worth considering even in
continuous domains. We were also able to deal with
a specific class of separable non-linear constraints.
In the future, we would like to better explore how
the integration bottleneck can be addressed, possibly
by caching sub-integration computations. In indepen-
dent recent efforts, (Martires et al., 2019; Kolb et al.,
2019) also investigate the use of SDDs for performing
WMI. In particular, (Kolb et al., 2019) consider a dif-
ferent type of mapping between WMI and SDDs but
do not consider non-linear domains, whereas (Mar-
tires et al., 2019) allow for standard density functions
such as Gaussians by appealing to algebraic model
counting (Kimmig et al., 2016). Performing addi-
tional comparisons and seeing how these ideas could
be incorporated in our framework might be an inter-
esting direction for the future.
ACKNOWLEDGEMENTS
Anton Fuxjaeger was supported by the Engineering
and Physical Sciences Research Council (EPSRC)
Centre for Doctoral Training in Pervasive Parallelism
(grant EP/L01503X/1) at the School of Informatics,
University of Edinburgh. Vaishak Belle was sup-
ported by a Royal Society University Research Fel-
lowship. We would also like to thank our reviewers
for their helpful suggestions.
REFERENCES
Albarghouthi, A., D’Antoni, L., Drews, S., and Nori, A.
(2017). Quantifying Program Bias. arXiv e-prints,
page arXiv:1702.05437.
ICAART 2020 - 12th International Conference on Agents and Artificial Intelligence
354

Bahar, R. I., Frohm, E. A., Gaona, C. M., Hachtel, G. D.,
Macii, E., Pardo, A., and Somenzi, F. (1997). Alge-
bric decision diagrams and their applications. Formal
methods in system design, 10(2-3):171–206.
Baldoni, V., Berline, N., De Loera, J., K
¨
oppe, M., and
Vergne, M. (2011). How to integrate a polyno-
mial over a simplex. Mathematics of Computation,
80(273):297–325.
Barrett, C. W., Sebastiani, R., Seshia, S. A., and Tinelli, C.
(2009). Satisfiability modulo theories. In (Biere et al.,
2009), pages 825–885.
Bekker, J., Davis, J., Choi, A., Darwiche, A., and Van den
Broeck, G. (2015). Tractable learning for complex
probability queries. In Advances in Neural Informa-
tion Processing Systems, pages 2242–2250.
Belle, V., Passerini, A., and Van den Broeck, G. (2015).
Probabilistic inference in hybrid domains by weighted
model integration. In Proceedings of 24th Interna-
tional Joint Conference on Artificial Intelligence (IJ-
CAI), pages 2770–2776.
Belle, V., Van den Broeck, G., and Passerini, A. (2016).
Component caching in hybrid domains with piecewise
polynomial densities. In Proceedings of the 30th Con-
ference on Artificial Intelligence (AAAI).
Biere, A., Biere, A., Heule, M., van Maaren, H., and Walsh,
T. (2009). Handbook of Satisfiability: Volume 185
Frontiers in Artificial Intelligence and Applications.
IOS Press, Amsterdam, The Netherlands, The Nether-
lands.
Chavira, M. and Darwiche, A. (2008). On probabilistic in-
ference by weighted model counting. Artificial Intel-
ligence, 172(6-7):772–799.
Chistikov, D., Dimitrova, R., and Majumdar, R. (2017). Ap-
proximate counting in smt and value estimation for
probabilistic programs. Acta Informatica, 54(8):729–
764.
Choi, A. and Darwiche, A. (2013). Dynamic minimization
of sentential decision diagrams. In AAAI.
Choi, A., Kisa, D., and Darwiche, A. (2013). Compiling
probabilistic graphical models using sentential deci-
sion diagrams. In European Conference on Symbolic
and Quantitative Approaches to Reasoning and Un-
certainty, pages 121–132. Springer.
Darwiche, A. (2004). New advances in compiling cnf to
decomposable negation normal form. In Proceedings
of the 16th European Conference on Artificial Intelli-
gence, pages 318–322. Citeseer.
Darwiche, A. (2011). Sdd: A new canonical represen-
tation of propositional knowledge bases. In IJCAI
Proceedings-International Joint Conference on Arti-
ficial Intelligence, volume 22, page 819.
Darwiche, A. and Marquis, P. (2002). A knowledge compi-
lation map. Journal of Artificial Intelligence Research,
17(1):229–264.
De Loera, J., Dutra, B., Koeppe, M., Moreinis, S., Pinto,
G., and Wu, J. (2011). Software for exact integra-
tion of polynomials over polyhedra. arXiv preprint
arXiv:1108.0117.
De Loera, J. A., Hemmecke, R., Tauzer, J., and Yoshida,
R. (2004). Effective lattice point counting in rational
convex polytopes. Journal of symbolic computation,
38(4):1273–1302.
Fierens, D., Van den Broeck, G., Renkens, J., Shterionov,
D., Gutmann, B., Thon, I., Janssens, G., and De Raedt,
L. (2015). Inference and learning in probabilistic logic
programs using weighted boolean formulas. Theory
and Practice of Logic Programming, 15(3):358–401.
Gomes, C. P., Sabharwal, A., and Selman, B. (2009). Model
counting. In (Biere et al., 2009), pages 633–654.
Kimmig, A., Van den Broeck, G., and De Raedt, L. (2016).
Algebraic model counting. International Journal of
Applied Logic.
Kisa, D., Van den Broeck, G., Choi, A., and Darwiche, A.
(2014). Probabilistic sentential decision diagrams. In
KR.
Kolb, S., Mladenov, M., Sanner, S., Belle, V., and Kersting,
K. (2018). Efficient symbolic integration for proba-
bilistic inference. In IJCAI, pages 5031–5037.
Kolb, S., Zuidberg Dos Martires, P. M., and De Raedt,
L. (2019). How to exploit structure while solving
weighted model integration problems. UAI 2019 Pro-
ceedings.
Liang, Y., Bekker, J., and Van den Broeck, G. (2017).
Learning the structure of probabilistic sentential deci-
sion diagrams. In Proceedings of the 33rd Conference
on Uncertainty in Artificial Intelligence (UAI).
Martires, P., Dries, A., and De Raedt, L. (2019). Exact and
approximate weighted model integration with proba-
bility density functions using knowledge compilation.
Proceedings of the AAAI Conference on Artificial In-
telligence, 33:7825–7833.
Morettin, P., Passerini, A., and Sebastiani, R. (2017). Effi-
cient weighted model integration via smt-based predi-
cate abstraction. In Proceedings of the Twenty-Sixth
International Joint Conference on Artificial Intelli-
gence, IJCAI-17, pages 720–728.
Muise, C., McIlraith, S. A., Beck, J. C., and Hsu, E. I.
(2012). D sharp: fast d-dnnf compilation with sharp-
sat. In Canadian Conference on Artificial Intelligence,
pages 356–361. Springer.
Poon, H. and Domingos, P. (2011). Sum-product networks:
A new deep architecture. In Computer Vision Work-
shops (ICCV Workshops), 2011 IEEE International
Conference on, pages 689–690. IEEE.
Sang, T., Beame, P., and Kautz, H. A. (2005). Performing
bayesian inference by weighted model counting. In
AAAI, volume 5, pages 475–481.
Sanner, S., Delgado, K., and Barros, L. (2012). Sym-
bolic dynamic programming for discrete and contin-
uous state mdps. CoRR, abs/1202.3762.
Shenoy, P. P. and West, J. C. (2011). Inference in hy-
brid bayesian networks using mixtures of polynomi-
als. International Journal of Approximate Reasoning,
52(5):641–657.
Suciu, D., Olteanu, D., R
´
e, C., and Koch, C. (2011). Proba-
bilistic databases. Synthesis lectures on data manage-
ment, 3(2):1–180.
Van den Broeck, G. and Darwiche, A. (2015). On the role of
canonicity in knowledge compilation. In AAAI, pages
1641–1648.
Scaling up Probabilistic Inference in Linear and Non-linear Hybrid Domains by Leveraging Knowledge Compilation
355
