
Multiple Ellipse Detection by using RANSAC and DBSCAN Method
Kristian Sabo
a
and Rudolf Scitovski
b
Department of Mathematics, Josip Juraj Strossmayer University of Osijek, Trg Ljudevita Gaja 6, 31000 Osijek, Croatia
Keywords:
Multiple Ellipse Detection, Clustering, RANSAC, DBSCAN.
Abstract:
In this paper we consider one and multiple ellipse (represented as a Mahalanobis circle) detection problem
on the basis of data points coming from one or several ellipses not known in advance. For solving one
ellipse detection problem two methods are mentioned. These methods are used by solving the multiple ellipse
detection problem. The method proposed in this paper is based on the well-known RANSAC method using the
parameters MinPts and ε from the DBSCAN method. In this way the efficiency of choosing the best ellipse
among N ellipses given by the RANSAC method is improved. The local density
ˆ
ρ =
|
ˆ
π|
|
ˆ
E|
is determined for each
obtained ellipse
ˆ
E with circumference |
ˆ
E| and corresponding cluster
ˆ
π with |
ˆ
π| elements . If local density
ˆ
ρ is
smaller than lower bound
MinPts
2ε
of the local density of the whole set A, the ellipse
ˆ
E will be dropped. In order
to obtain the final solution, an Adaptive Mahalanobis k-means algorithm is applied on the remaining ellipses.
The method is illustrated on several examples with artificial data point sets and also on a few real images.
1 INTRODUCTION
Ellipse detection problem plays a specifically sig-
nificant role in different applications such as pat-
tern recognition and computer vision (Akinlar and
Topal, 2013), agriculture, astronomical and geologi-
cal shape segmentation, images analysis in medicine
(Grbi
´
c et al., 2016), robotics and object detection,
and other image processing (Moshtaghi et al., 2011;
Prasad et al., 2013), etc.
In our paper we consider one and multiple ellipse
detection problem on the basis of a data point set com-
ing from a number of ellipses in the plane, whereby
the edges of these ellipses do not have to be exact or
clear and the number of ellipses does not have to be
known in advance.
The paper is organized as follows. In the next
section the statement of the problem and DBSCAN-
parameters are defined. In Section 3 one ellipse de-
tection problem is considered. 2 Section 4 considers
the multiple ellipse detection problem. The method
based on the RANSAC method with parameters from
the DBSCAN-algorithm (Ester et al., 1996) is proposed.
Two illustrative examples are given. Finally, some
conclusions are given in Section 5.
a
https://orcid.org/0000-0002-1787-3161
b
https://orcid.org/0000-0002-7386-5991
2 STATEMENT OF THE
PROBLEM
Given is the set of data points in the plane A = {a
i
=
(x
i
, y
i
)
T
: i = 1, . . . , m} ⊂ ∆, ∆ = [a, b] ×[c,d] ⊂ R
2
,
a < b, c < d which is considered to be scattered along
multiple ellipses not known in advance and which
should be reconstructed or detected. Additionally, we
suppose that the subset of data points π(E) ⊂ A com-
ing from some ellipse E satisfies the “homogeneity
property”, i.e. we assume that the set π(E) is uni-
formly scattered around ellipse E, and the number
ρ(π) =
|π(E)|
|E|
, (1)
where |E| is the length of the ellipse E, will be called
the local density of data point set π(E).
By using the parameters MinPts and ε(A) from
the DBSCAN method (Ester et al., 1996) it is possi-
ble to estimate the lower bound for the local den-
sity of the whole set A. According to (Scitovski and
Sabo, 2019b) we determine the parameter MinPts =
blog|A|c and parameter ε(A) in the following way.
For each a ∈ A we determine radius ε
a
> 0 of the
smallest disc centered at a and containing at least
MinPts elements of the set A . Then 99.5% quantile
of the set {ε
a
: a ∈A} is marked with ε(A).
Remark 1. Since for almost all points a ∈A the cor-
responding disc with the center a and the radius ε(A)
Sabo, K. and Scitovski, R.
Multiple Ellipse Detection by using RANSAC and DBSCAN Method.
DOI: 10.5220/0008879301290135
In Proceedings of the 9th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2020), pages 129-135
ISBN: 978-989-758-397-1; ISSN: 2184-4313
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
129

contains at least MinPts elements of the set A, the
lower bound of the local density ρ(A) of the whole
set A can be estimated with
MinPts
2ε(A)
.
Now, let us define the Multiple Ellipse Detection
problem (Akinlar and Topal, 2013; Grbi
´
c et al., 2016;
Maro
ˇ
sevi
´
c and Scitovski, 2015). If the number k ≥ 1
of ellipses is known in advance, the problem is con-
sidered as follows. For the given set of data points
A one should estimate the unknown parameters of el-
lipses E
j
(p
j
, q
j
, ξ
j
, η
j
, ϑ
j
), j = 1, . . . , k:
x(t)
y(t)
=
p
j
q
j
+U(ϑ)
ξ
j
cost
η
j
sint
, t ∈ [0,2π], (2)
where S
j
= (p
j
, q
j
)
T
are the centers, ξ
j
, η
j
> 0 are
the lengths of semiaxes, ϑ
j
are the angles and U (ϑ) =
cosϑ −sin ϑ
sinϑ cosϑ
are the matrices of rotation, by solv-
ing the following global optimization problem
argmin
p,q,ξ,η,ϑ
F(p, q, ξ, η, ϑ), (3)
F(p, q, ξ, η, ϑ) =
m
∑
i=1
min
1≤j≤k
D(a
i
, E
j
(p
j
, q
j
, ξ
j
, η
j
, ϑ
j
)),
where D is some distance-like function defining the
distance from a point a ∈ A to the ellipse E
j
(for ex-
ample, like (11)).
If E is understood as the cluster center (E-cluster-
center), then multiple ellipse detection problem (3)
can be interpreted as the problem of searching for a
k-globally optimal partition Π = {π
1
, . . . , π
k
}
argmin
Π∈Part(A;k)
F (Π), (4)
F (Π) =
k
∑
j=1
∑
a
i
∈π
j
D(a
i
, E
j
),
where E
j
is perceived as the E-cluster-center of clus-
ter π
j
and Part(A; k) is the set of all k-partitions of the
set A (Morales-Esteban et al., 2014; Scitovski and Sc-
itovski, 2013).
The minimizing function F is nonconvex and
nondifferentiable, but, similarly as in (Scitovski and
Sabo, 2019a), it can prove to be Lipschitz-continuous.
In order to solve the global optimization problem
(3) we can apply one of the known global optimiza-
tion methods (Horst and Tuy, 1996; Paulavi
ˇ
cius and
ˇ
Zilinskas, 2014). For example, one could try to
solve the problem by using the well-known DIRECT
global optimization algorithm (Grbi
´
c et al., 2013;
Jones et al., 1993). However, due to the property of
the DIRECT algorithm to search for all points of the
global minimum, using this algorithm would prove to
be a very inefficient procedure (Scitovski and Sabo,
2019a).
In the case of an unknown number of ellipses us-
ing, for example, incremental method (see Grbi
´
c et al.
(2016); Bagirov et al. (2011)), an optimal k-partition
for k = 1, 2, . . . is searched for. After that, by using
some indexes adapted for E-cluster-centers (see e.g.
Grbi
´
c et al. (2016); Scitovski and Sabo (2020)), a par-
tition with the most appropriate number of clusters
can be determined.
There are several methods known for solving this
problem in the literature. Most of them are based
on the Hough transform (Mukhopadhyay and Chaud-
huri, 2015), center based clustering (Maro
ˇ
sevi
´
c and
Scitovski, 2015; Moshtaghi et al., 2011; Morales-
Esteban et al., 2014) or geometric method (Isack and
Boykov, 2012; Prasad et al., 2013). The method
EDCircles proposed in Akinlar and Topal (2013) can
be used in real-time applications.
3 DETECTION OF ONE ELLIPSE
We first consider one ellipse detection problem in the
plane. An ellipse in the plane can be defined as a set of
points {(x, y)
T
∈R
2
: P(x, y) = 0}, where (Fitzgibbon
et al., 1999)
P(x, y) = ax
2
+ 2bxy + cy
2
+ dx + ey + f , (5)
where ac −b
2
= 1. For a given set A the optimal
values of parameters a, b, c, d, e, f , g can be obtained
by solving a constrained linear Least Squares problem
argmin
a,b,c,d,e, f ∈R
ac−b
2
=1
m
∑
i=1
(P(x
i
, y
i
))
2
, (6)
and can be written in the standard form (2), as shown
in the next subsection.
3.1 An Ellipse as a Mahalanobis Circle
An ellipse E(S, ξ, η, ϑ), S = (p, q)
T
, written in the
standard form (2), can be interpreted as a “unit” Ma-
halanobis circle (M-circle)
E = {u ∈ R
2
: (S −u)
T
Σ
−1
(S −u) = 1)}, (7)
where Σ = (σ
i j
) ∈ R
2×2
is the positive definite ma-
trix with eigenvalues ξ
2
, η
2
. Due to the insurance
of the monotonicity property of the k-means algo-
rithm, a normalized Mahalanobis distance-like func-
tion d
M
: R
2
×R
2
→ R
+
,
d
M
(u, v;Σ) :=
√
detΣ(u −v)
T
Σ
−1
(u −v)
= ku −vk
2
Σ
(8)
is introduced.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
130

An ellipse E(S,ξ, η, ϑ) can be written as M-circle
(Scitovski and Sabo, 2019a)
E(S,r, Σ) = {u ∈R
2
: d
M
(S, u; Σ) = r
2
}, (9)
where r
2
=
√
detΣ = ξη and conversely, an M-circle
corresponds to the ellipse E(S,ξ, η, ϑ), where
diag(ξ
2
, η
2
) = U
r
2
√
detΣ
Σ
U
T
, (10)
U =
cosϑ −sin ϑ
sinϑ cosϑ
, ϑ =
1
2
arctan
2σ
12
σ
11
−σ
22
.
Also, we can now define the algebraic distance
from the point a ∈ R
2
to the ellipse E (Morales-
Esteban et al., 2014; Maro
ˇ
sevi
´
c and Scitovski, 2015)
D(a, E) = (kS −ak
2
Σ
−r
2
)
2
, (11)
where kS −ak
2
Σ
= d
M
(a, S; Σ). Similarly, we could de-
fine Total Least Squares distance and Least Absolute
Deviations distance (Grbi
´
c et al., 2016).
3.2 An Ellipse Detection by using
Locally Optimization Method
For recognizing an ellipse on the basis of given set
of data points A which comes from an ellipse not
known in advance we apply some local optimization
method (Newton, Quasi-Newton (Dennis and Schn-
abel, 1996)). For that purpose, it is necessary to
have a good initial approximation. A very good ini-
tial approximation is (see Scitovski and Sabo (2019b,
2020)):
S
0
= Mean[A ], (12)
where Σ
0
=
1
m
∑
a∈A
(S
0
−a)(S
0
−a)
T
and
r
0
=
1
m
∑
a∈A
kS
0
−ak
2
Σ
0
,
because
∑
a∈A
kS
0
−ak
2
Σ
0
−r
2
2
≥
∑
a∈A
kS
0
−ak
2
Σ
0
−
1
m
∑
a∈A
kS
0
−ak
2
Σ
0
2
.
Note that the matrix Σ
0
is a covariance matrix written
using the Kronecker product.
Example 1. Data point set which comes from the el-
lipse E((5, 5), 5, 2,
π
4
) is shown in Fig. 1a (Grbi
´
c et al.,
2016). The corresponding initial approximation ob-
tained by (12) gives the ellipse shown in Fig. 1b. The
final solution obtained by Newton (Dennis and Schn-
abel, 1996) method is shown in Fig. 1c.
2 4 6 8 10
2
4
6
8
10
(a) Data points
2 4 6 8 10
2
4
6
8
10
(b) Initial approximation
2 4 6 8 10
2
4
6
8
10
(c) Solution
Figure 1: One ellipse detection using local optimization
method.
3.3 Ellipse Detection using the RANSAC
and the DBSCAN Method
RANSAC-method is proposed in the paper Fischler and
Bolles (1981). There are different areas of applica-
tions with this method (see e.g. Cupec et al. (2009);
Isack and Boykov (2012)). In our paper we also apply
this method to solve one and multiple ellipse detection
problem.
An ellipse in the form (5) can be determined on the
basis of several data points from the set A by solving
constrained linear Least Squares problem (6). For ex-
ample, if five chosen points (x
1
, y
1
)
T
, . . . , (x
5
, y
5
)
T
∈
A do not lie on a line, i.e. if the rank of the matrix
1 x
1
y
1
.
.
.
.
.
.
.
.
.
1 x
5
y
5
is equal to 3, we obtain an ellipse candi-
date E, which shall be written in the form of M-circle
E(S,r, Σ). Additionally, if E ⊂ ∆, we assume to have
gotten an acceptable candidate for the ellipse. Finally,
in the ε(A)-neighborhood of the acceptable ellipse we
determine the number of points from the set A. We
repeat the procedure N times (say, 10) and keep that
ellipse
ˆ
E for which the corresponding set of points is
the largest.
Ellipse
ˆ
E, written in the form of M-circle
ˆ
E(
ˆ
S, ˆr,
ˆ
Σ),
is a good initial approximation for the ellipse which
will be searched for by solving the local optimization
problem for the function
F(S, r, Σ) =
m
∑
i=1
D(a
i
, E(S,r, Σ)), (13)
with the initial approximation {
ˆ
S, ˆr,
ˆ
Σ}.
Example 2. The data point set which comes from the
ellipse E((5, 5), 5, 2,
π
4
) is shown in Fig. 1a (see also
Multiple Ellipse Detection by using RANSAC and DBSCAN Method
131

Grbi
´
c et al. (2016)). After N = 8 iterations we got five
points which resulted in the ellipse shown in Fig. 2a.
The final solution obtained by the Newton method is
shown in Fig. 2b and coincides with the ellipse ob-
tained in Example 1.
0 2 4 6 8 10
0
2
4
6
8
10
(a) Initial approximation
2 4 6 8 10
2
4
6
8
10
(b) Solution
Figure 2: One ellipse detection using the RANSAC method.
4 THE MULTIPLE ELLIPSE
DETECTION PROBLEM
Now, let us suppose that the data point set A comes
from several ellipses in the plane not known in ad-
vance. We will search for the solution of the multiple
ellipse detection problem by solving global optimiza-
tion problem (3), where D is the algebraic distance
given by (11). Unfortunately, direct application of
the well-known clustering method (see e.g. Domeni-
coni et al. (2016); Scitovski and Scitovski (2013)) is
impossible. Also, the method described in Subsec-
tion 3.2 cannot be applied in this case. For solving
this problem we show a generalization of the method
described in Subsection 3.3. The corresponding algo-
rithm will be called RANSAC for multiple ellipse detec-
tion problem (or abbreviated, RM-algorithm) and will
be described in the following way.
First, we randomly choose 5 points from the set A
not lying on the line. The ellipse determined on the
basis of these points by (6) and contained in rectangle
∆ is an acceptable candidate for the searched ellipse.
We write this ellipse in the form of M-circle E(S, r, Σ).
By repeating the procedure, we assume that we have
found N candidates. In this case the choice of ellipse
in whose ε(A)-neighborhood is the largest number of
points from the set A is no longer an acceptable cri-
terion for the best ellipse as it was in the case of one
ellipse detection (Subsection 3.3).
In multiple ellipse-case we will suppose that the
best ellipse
ˆ
E has the largest local density (1) of points
in its ε(A)-neighborhood. The cluster
ˆ
π := {a ∈
A : D(a,
ˆ
E) < ε(A)} ⊂ A of points from this ε(A)-
neighborhood should be dropped from the set A and
the procedure should be repeated on the rest of the set
A \
ˆ
π.
We repeat the whole procedure until the number of
the remaining sets becomes smaller than some num-
ber given in advance (for example, 5 MinPts). In that
way we obtain κ ellipses
ˆ
E
j
, j = 1, . . . , κ.
Furthermore, we determine the local density
ˆ
ρ
j
(
ˆ
E
j
) =
|
ˆ
π
j
|
|
ˆ
E
j
|
for each pair (
ˆ
π
j
,
ˆ
E
j
), where |
ˆ
π
j
| is the
number of points in the cluster
ˆ
π
j
, and |
ˆ
E
j
| is the
length (circumference) of the ellipse
ˆ
E
j
which can be
estimated using the well-known Ramanujan approxi-
mation
|
ˆ
E
j
| ≈π(
ˆ
ξ
j
+
ˆ
η
j
)
1 +
3h
10+
√
4−3h
, (14)
where h =
(
ˆ
ξ
j
−
ˆ
η
j
)
2
(
ˆ
ξ
j
+
ˆ
η
j
)
2
Note that, for that purpose, it will
be necessary to write the ellipse
ˆ
E
j
in the standard
form
ˆ
E
j
(
ˆ
S
j
,
ˆ
ξ
j
,
ˆ
η
j
,
ˆ
ϑ
j
) (see Subsection 3.1).
Using the lower bound for the local density of the
set A (see Section 2), the ellipses, for which (see Re-
mark 1)
ˆ
ρ
j
(
ˆ
E
j
) <
MinPts
2ε(A)
, (15)
will be dropped. We apply the Adaptive Mahalanobis
k-means algorithm to all the remaining ellipses (Grbi
´
c
et al., 2016; Maro
ˇ
sevi
´
c and Scitovski, 2015; Morales-
Esteban et al., 2014). The algorithm can be described
in following two steps which are repeated iteratively:
Step A: (Assignment step) For each set of mutu-
ally different M-circles E
1
(S
1
, r
1
, Σ
1
), . . . ,
E
k
(S
k
, r
k
, Σ
k
), the set A should be divided
into k disjoint nonempty clusters π
1
, . . . , π
k
by using the minimal distance principle;
Step B: (Update step) Given a partition
Π{π
1
, . . . , π
k
} of the set A , one can de-
fine the corresponding M-circle-centers
ˆ
E
j
(
ˆ
S
j
, ˆr
j
,
ˆ
Σ
j
) j = 1, . . . , k by using the
methods described in Subsection 3.2 or
Subsection 3.3;
Set E
j
(S
j
, r
j
, Σ
j
) =
ˆ
E
j
(
ˆ
S
j
, ˆr
j
,
ˆ
Σ
j
) for
j = 1,. . . , k;
Remark 2. Note that, in this way, the remaining el-
lipses will be similar to the original ones. Therefore,
it will not be necessary to use indexes for detecting
the most appropriate partition with ellipses-cluster-
centers in the RM-algorithm.
Note also that searching for new five randomly
chosen points in the RM-algorithm can be repeated so
long until the local density for obtained ellipse be-
comes greater than the lower bound
MinPts
2ε(A)
.
Example 3. Let us consider the data point set A
shown in Fig. 3a which comes from three ellipses.
The number of points is |A| = 563, and DBSCAN-
parameters are MinPts = 6, and ε(A) = 0.378. The
lower bound for the local density of whole set A in
this case is 15.9.
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
132
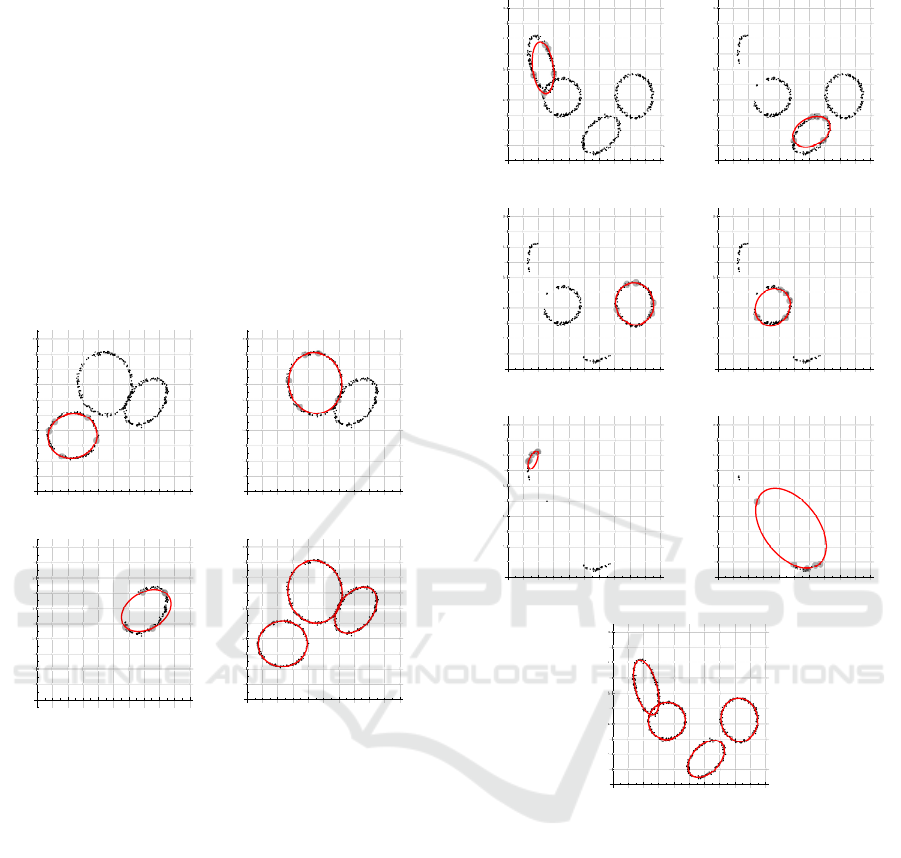
In order to detect ellipses from which the data
point set A comes, we apply the RM-algorithm for el-
lipses detection. First, the red ellipse shown in Fig. 3a
is obtained in 4
th
attempt. By dropping the points
in its ε(A)-neighborhood, the set of points shown in
Fig. 3b remains. After that, the next red ellipse shown
in Fig. 3b is obtained in 6
th
attempt. By dropping
the points in its ε(A )-neighborhood, the set of points
shown in Fig. 3c remains. Finally, the third red ellipse
shown in Fig. 3c is obtained in 5
th
attempt. By drop-
ping the points in its ε(A )-neighborhood, not a single
point of the set A remains. By applying Adaptive Ma-
halanobis k-means algorithm, three ellipses shown in
Fig. 3d are detected.
2 4 6 8 10
2
4
6
8
10
(a) Att.4: ρ(π
1
) = 18.7
2 4 6 8 10
2
4
6
8
10
(b) Att.6: ρ(π
1
) = 19.0
2 4 6 8 10
2
4
6
8
10
(c) Att.5: ρ(π
1
) = 17.0
2 4 6 8 10
2
4
6
8
10
(d) k-means algorithm
Figure 3: Three ellipses detection from Example 3.
Example 4. Let us consider data point set A shown
in Fig. 4a which comes from four ellipses. The num-
ber of points is |A |= 669 and DBSCAN-parameters are
MinPts = 6 and ε(A) = 0.284. Let us show how the
RM-algorithm can be applied in this case. The lower
bound for the local density in that case is 10.6.
In order to detect the ellipses, from which the data
point set A comes, we apply the RM-algorithm for el-
lipses detection. First, the red ellipse shown in Fig. 4a
is obtained in 61
st
attempt. By dropping the points
in its ε(A)-neighborhood, the set of points shown in
Fig. 4b remains. After that, the next red ellipse shown
in Fig. 4b is obtained in 96
th
attempt. By dropping
the points in its ε(A )-neighborhood, the set of points
shown in Fig. 4c remains. Furthermore, the next red
ellipse shown in Fig 4d is obtained in 103
rd
attempt.
By dropping the points in its ε(A )-neighborhood, the
set of points shown in Fig. 4e remains. After that,
the next red ellipse shown in Fig 4e is obtained in
17
th
attempt. By dropping the points in its ε(A)-
2 4 6 8 10
2
4
6
8
10
(a) Att.61: ρ(π
1
) = 22.6
2 4 6 8 10
2
4
6
8
10
(b) Att.96: ρ(π
2
) = 17.6
2 4 6 8 10
2
4
6
8
10
(c) Att.103: ρ(π
3
) = 21.0
2 4 6 8 10
2
4
6
8
10
(d) Att.167: ρ(π
4
) = 17.1
2 4 6 8 10
2
4
6
8
10
(e) Att.17: ρ(π
5
) = 9.6
2 4 6 8 10
2
4
6
8
10
(f) Att.5: ρ(π
6
) = 2, 4
2 4 6 8 10
2
4
6
8
10
(g) k-means algorithm
Figure 4: Based on the data point set from Example 4, the
RM-algorithm has detected four ellipses.
neighborhood, the set of points shown in Fig. 4f re-
mains. Finally, the next red ellipse shown in Fig 4f
is obtained in 5
th
attempt. By dropping the points in
its ε(A)-neighborhood, 5 points of the set A remain
remaining and theRM-algorithm is finished.
The clusters corresponding to the first four ellipses
have a local density greater than lower bound 10.6,
and the last two ellipses have a local density less than
the lower bound. Therefore, the last two ellipses will
be dropped, and the k-means algorithm will be ap-
plied to the remaining four ellipses. The results are
shown in Fig. 4g.
Note that the RM-algorithm does not require the
use of indexes for recognizing the most appropriate
partition with ellipse-cluster-centers. One can try to
Multiple Ellipse Detection by using RANSAC and DBSCAN Method
133

improve the efficiency of the method by multistarting
the method.
4.1 Real-world Problems
The proposed method for solving the multiple ellipse
detection problem can also be applied to real images.
For that purpose, we carried out the preprocessing of
the edge detection by using the Canny filter first (see
Bradski (2000); Wolfram Research (2016)).
In Fig 5a a fetal head detection on an ultrasound
image is shown. Corresponding edge curves obtained
by Canny filter in Fig 5b are shown. The red ellipse
in Fig 5a denotes the fetal head. Similarly, in Fig 6,
a detection problem for several cups on the table is
considered.
(a) Detection (b) Canny filter
Figure 5: Real image.
(a) Detection (b) Canny filter
Figure 6: Real image.
5 CONCLUSIONS
Solving multiple ellipse detection problem is impor-
tant in many applications. In our paper one and mul-
tiple ellipse detection problem are considered on the
basis of a data point set coming from a number of el-
lipses with noisy edges in the plane. Thereby, we sup-
pose that the subset of data points coming from some
ellipse satisfies the “homogeneity property”. For that
situation, a method based on the RANSAC-method is
proposed, whereby the DBSCAN-parameters MinPts
and ε play a significantly important role.
It is important to note that the RM-algorithm
does not require the use of indexes for recognizing
the most appropriate partition with ellipse-cluster-
centers. This is the basic advantage of this method
regarding the method EDCircles given in (Akinlar
and Topal, 2013) and method given in (Grbi
´
c et al.,
2016). Unlike our method, EDCircles does not rec-
ognize an ellipse with semi-axes (ξ, η),
ξ
η
≥ 4 and
cannot detect a single ellipse with a clear edge if
its shape departs significantly from a circular shape.
However, our method requires more computing time
than EDCircles.
The method proposed in our paper could be ap-
plied to the case of other geometrical objects too, but
its application is also possible in 3D.
ACKNOWLEDGEMENTS
The author would like to thank the referees and the
journal editors for their careful reading of the pa-
per and insightful comments that helped us improve
the paper. Especially, the author would like to thank
Mrs. Katarina Mor
ˇ
zan for significantly improving the
use of English in the paper. This work was supported
by the Croatian Science Foundation through research
grants IP-2016-06-6545 and IP-2016-06-8350.
REFERENCES
Akinlar, C. and Topal, C. (2013). Edcircles: A real-time cir-
cle detector with a false detection control. Pattern Recog-
nition, 46:725–740.
Bagirov, A. M., Ugon, J., and Webb, D. (2011). Fast mod-
ified global k-means algorithm for incremental cluster
construction. Pattern Recognition, 44:866–876.
Bradski, G. (2000). The opencv library, Dr. Dobb’s Journal
of Software Tools.
Cupec, R., Grbi
´
c, R., Sabo, K., and Scitovski, R. (2009).
Three points method for searching the best least absolute
deviations plane. Applied Mathematics and Computa-
tion, 215:983–994.
Dennis, J. J. and Schnabel, R. (1996). Numerical Methods
for Unconstrained Optimization and Nonlinear Equa-
tions. SIAM, Philadelphia.
Domeniconi, G., Semertzidis, K., Lopez, V., Daly, E. M.,
Kotoulas, S., and Moro, G. (2016). A novel method
for unsupervised and supervised conversational message
thread detection. In Proceedings of the 5th International
Conference on Data Management Technologies and Ap-
plications (DATA 2016) ISBN:, pages 43–54.
Ester, M., Kriegel, H., and Sander, J. (1996). A density-
based algorithm for discovering clusters in large spatial
databases with noise. In 2nd International Conference
on Knowledge Discovery and Data Mining (KDD-96),
pages 226–231, Portland.
Fischler, M. and Bolles, R. (1981). Random sample con-
sensus: a paradigm for model fitting with applications to
ICPRAM 2020 - 9th International Conference on Pattern Recognition Applications and Methods
134

image analysis and automated cartography. Communica-
tions of the ACM, 24:381–395.
Fitzgibbon, A., Pilu, M., and Fisher, R. B. (1999). Direct
least square fitting of ellipses. IEEE Transactions on Pat-
tern Analysis and Machine Intelligence, 21:476–480.
Grbi
´
c, R., Grahovac, D., and Scitovski, R. (2016). A
method for solving the multiple ellipses detection prob-
lem. Pattern Recognition, 60:824–834.
Grbi
´
c, R., Nyarko, E. K., and Scitovski, R. (2013). A mod-
ification of the DIRECT method for Lipschitz global op-
timization for a symmetric function. Journal of Global
Optimization, 57:1193–1212.
Horst, R. and Tuy, H. (1996). Global Optimization: Deter-
ministic Approach. Springer, 3rd, revised and enlarged
edition.
Isack, H. and Boykov, Y. (2012). Energy-based geometric
multi-model fitting. International Journal of Computer
Vision, 97:123–147.
Jones, D. R., Perttunen, C. D., and Stuckman, B. E.
(1993). Lipschitzian optimization without the Lipschitz
constant. Journal of Optimization Theory and Applica-
tions, 79:157–181.
Maro
ˇ
sevi
´
c, T. and Scitovski, R. (2015). Multiple ellipse
fitting by center-based clustering. Croatian Operational
Research Review, 6:43–53.
Morales-Esteban, A., Mart
´
ınez-
´
Alvarez, F., Scitovski, S.,
and Scitovski, R. (2014). A fast partitioning algorithm
using adaptive Mahalanobis clustering with application
to seismic zoning. Computers & Geosciences, 73:132–
141.
Moshtaghi, M., Havens, T. C., Bezdek, J. C., Park,
L., Leckie, C., Rajasegarar, S., Keller, J. M., and
Palaniswami, M. (2011). Clustering ellipses for anomaly
detection. Pattern Recognition, 44:55–69.
Mukhopadhyay, P. and Chaudhuri, B. B. (2015). A survey
of Hough transform. Pattern Recognition, 48:993–1010.
Paulavi
ˇ
cius, R. and
ˇ
Zilinskas, J. (2014). Simplicial Global
Optimization. Springer.
Prasad, D. K., Leung, M. K. H., and Quek, C. (2013). Elli-
fit: An unconstrained, non-iterative, least squares based
geometric ellipse fitting method. Pattern Recognition,
46:1449–1465.
Scitovski, R. and Sabo, K. (2019a). Application of the DI-
RECT algorithm to searching for an optimal k-partition
of the set A and its application to the multiple circle
detection problem. Journal of Global Optimization,
74(1),:63–77.
Scitovski, R. and Sabo, K. (2019b). DBSCAN-like cluster-
ing method for various data densities. Pattern Analysis
and Applications. DOI: 10.1007/s10044-019-00809-z.
Scitovski, R. and Sabo, K. (2020). The adaptation of the
k-means algorithm to solving the multiple ellipses detec-
tion problem by using an initial approximation obtained
by the DIRECT global optimization algorithm. Applica-
tions of Mathematics. (accepted for publication).
Scitovski, R. and Scitovski, S. (2013). A fast partitioning
algorithm and its application to earthquake investigation.
Computers & Geosciences, 59:124–131.
Wolfram Research, I. (2016). Mathematica. Wolfram Re-
search, Inc., Champaign, Illinois, version 11.0 edition.
Multiple Ellipse Detection by using RANSAC and DBSCAN Method
135
