
Fractal Generating Techniques
Younes S. Alwan
1a
, Khalid Saeed Lateef Al-badri
2b
, Ghazwan S. Alwan
3
and Marwah Q. Majeed
4
1
Electromechanical Engineering Dept., University of Samarra, Samarra City, Saladin, Iraq
2
Physics Dept., University of Samarra, Samarra City, Saladin, Iraq
3
Mechanical Engineering Dept., University of Tikrit, Tikrit City, Saladin, Iraq
4
Civil Engineering Dept., University of Samarra, Samarra City, Saladin, Iraq
Keywords: Fractal, Fractal Generator, Generation Techniques.
Abstract: Globally, researchers have been trying to produce the most comprehensive description of introducing fractals
and utilizing them in different sciences. Their effort lies in elaborating and recruiting the scope of fractals in
science and applications, such as antenna design, computer software programming. Further, the modern world
needs the products to be compact, efficient and economically suitable, where fractals bring such
recommendations. In this review article, we present a briefed description of fractals, types of fractals, merits
of fractals and, most importantly, fractal generator techniques along with their mathematical techniques and
software.
1 INTRODUCTION
In mathematics, a fractal is a complete, iterative-like,
and self-alike mathematical set whose Hausdorff
aspect or direction firmly overrides its topological
dimension. Fractals are available universally in nature
because of their predisposition to seem approximately
identical at different aspects, as appears in the
consecutively trivial amplifications of the Mandelbrot
set. Further, fractals have alike arrangements at
progressively small sizes that is similarly known as
intensifying symmetry or unfolding symmetry
(Mandelbrot, 1983). When this repetition is strictly the
same as the relating generated almost same copy at
every scale, like what appears in the Menger sponge, a
fractal has a self-similar arrangement.
Fractal is an, somehow, irregular or disjointed
geometric shape, which can be sub-partitioned in
parts, where each part is roughly a smaller copy of a
whole fractal object (Paul, 1991). It is a natural
phenomenon or a mathematical expression, which has
a repeating pattern that displays at every scale. If the
replication is the same at every scale, it is called a
self-similar pattern. Fractals can also be nearly the
same at different levels and includes the idea of a
a
https://orcid.org/0000-0002-9133-4705
b
https://orcid.org/0000-0003-3678-4954
detailed pattern that repeats itself. As seen in nature,
most physical systems, structures, objects and works
are not east-to-recognize systematic geometric and
are not mathematically calculated shapes of the
standard geometry.
Many patterns of fractals can be generated by
utilizing inspirations from the areas of natural
sciences. An example of such an inspiration is the
diffusion-limited aggregation (DLA) that describes,
apart from other descriptions, the diffusion-
aggregation of zinc ions in an electrolytic solution on
electrodes. Other examples of naturally generated
fractals because of their ultimate structure are the
flowers, vegetables, etc. Fractal would appear when
analyzing ice particles; hence, it shows a dramatic
presentation of fractal growths as monitored by
utilizing a specialized telescopic tool. Further, fractal
shows itself in the structure of many living organs and
bodies of animals. For instance, fractal patterns have
a critical role in fortifying and shaping the shell in
snails, where their shells revolve in an obvious way
of fractal shape. Such observation is noticeable in
almost every aspect of life (Douglas et al., 2003). In
addition, Large-scale objects like galaxies and small-
scale items like atoms are all offering different forms
of fractal generating initiatives. Moreover, movements,
motion, and interpolation mathematical processes in
science exhibit stochastic models that contain fractal
behavior; hence, every single item in the universe can
initiate a fractal behavior at some point.
This reviewing work is mostly dedicated for the
techniques by which fractals are generated, because
fractals have templates and/or functions with a
prototype item. At that point, the prototype grows
within some patterns to build the whole structure of
the fractal body. The paper, however, has been
divided into many divisions to comprehend and
visualize a full panorama of what to discuss about
fractal initiation and how to generate fractals. The
first division talks about an explanation of where the
idea of fractals have come from. In the next division,
merits of utilizing fractals are discussed, whereas the
following section collects many fractal generation
techniques with some supporting explanation.
Moreover in this work, the next section depicts the
mathematical representation of fractal generation.
Before the conclusion and references, the final
section mentions the computer software programs
dedicated for fractals.
2 FRACTALS CONCEPT
There have been tremendous number of researchers
and mathematicians around the globe trying to
elaborate the key philosophy of the fractal spreading
in the universe. The apparent behavior of natural
fractal pattern expose an attitude of the nature to build
living and non-living objects that mimic their own
items; i.e. as if the nature’s printer types the same
generator with different scaling factors to have such
infinite-like patterns; hence, nature would select the
simplest procedure to fill space and size. At that point,
the simplest way would be to accumulate almost-
similar structures in, somehow, different styles to
expose the final product.
Artificial fractals are useful to express and
modulate objects that may contain a base to start
from, such as decorations, computer images, civil
structures, architecture, interpolation, engineering
tools, economics, etc. The most important merit of
artificial fractals is the ability to comprehend current
solution needs and to create the suitable fractal
texture that fits the different desires. On the other
hand, natural fractals follow the needs of nature,
without an exact explanation as mentioned earlier.
However, it still needs further discovery to explain
the origin of fractals and why/how it has reached such
forms, but it is probably not able to explain without
utilizing deeper physical, mathematical theories and
maybe super computers and algorithms.
3 MERITS OF USING FRACTALS
Fractals have grabbed many properties into account,
inspired primarily from nature. Depending on the
field that uses iterative geometric properties, merits
of fractals can be classified into some items as listed
(Douglas et al., 2003).
1. In-fit size structure.
2. Low profile packages
3. Conformal
4. Broadband and/or multiband
5. Fast growing attitude
6. Predictable approach throughput
7. Easiness of programming and modelling
8. Fashion style and artistic design
9. Forecast of many life representations
10. Key to explain prospective and existing
theorems.
According to the aforementioned and other
properties, fractals and similar geometric designs
have become the desirable figures with respect to
researchers, designers, and programmers.
4 AGGREGATION OF SOME
FRACTAL GENERATION
FIGURES
Over ages, mathematicians and scientists have found
and developed fractal shapes depending on the
application they intend to adopt. This section presents
a comprehensive overview of some common fractal
geometries that have been developed or discovered.
These designs have been used in developing modern
and innovative designs of technological and
engineering system structures, such as demographic
mapping, computer software, systems models,
microwave assemblies and antennas.
4.1 Sierpinski Gasket
The first iterations in the construction of the
Sierpinski gasket are shown in Figure 1. The process
of the geometry of such construction is a fractal
beginning with an equilateral triangle, as illustrated in
the first stage of Figure 1. The next iteration in the
construction is to remove a central triangle that is
located at the mid of the original triangle. This newly
removed triangle has vertices at the centers of each
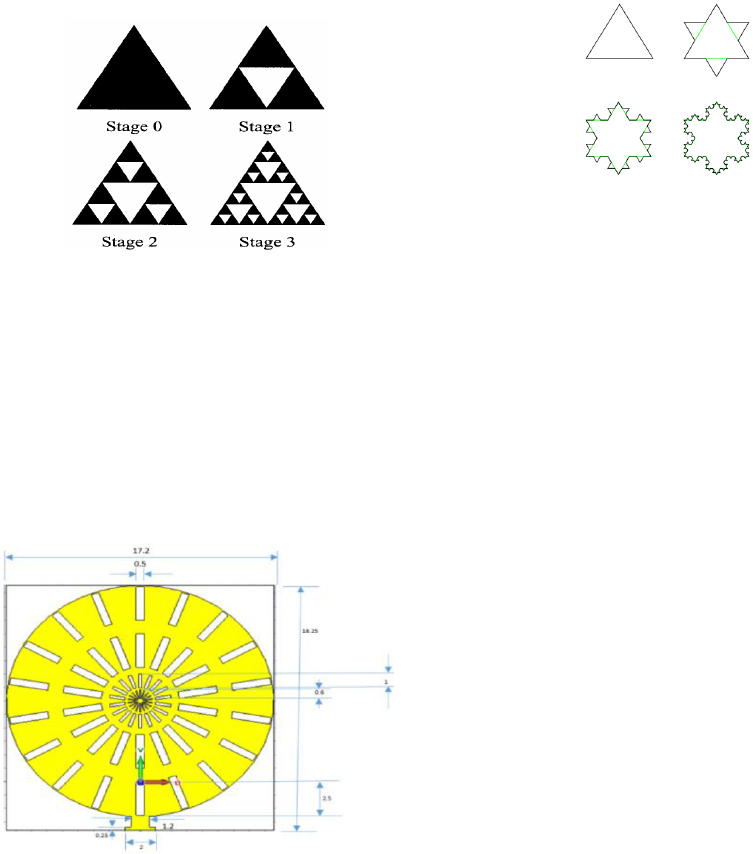
side of the original triangle as shown in Stage 1. This
process repeats itself for the remaining three
triangles, as shown in Stage 2, 3, and 4 for the same
figure. Consequently, the Sierpinski-gasket fractal is
generated by carrying out this consecutive process an
infinite amount of times. Further, Sierpinski gasket is
an example of a generally self-similar fractal. From
an RF engineering viewpoint, a practical clarification
of Figure (1) is that the black triangular areas
characterize a metallic conductor; while the white
triangular areas characterize regions where metal has
been removed (Douglas et al., 2003).
Figure 1: Sierpinski-gasket fractal construction.
4.2 Fracal by Entrenches
In this design, a new idea of patterning a fractal antenna
comes in a reality, where a circular patch that contains
entrenches was utilized in this process, as shown in
Figure 2. The process of this design takes the manner
of internally enclosed circles of entrenches. Further,
the first far tire has a designated number of slots, where
other tires have the same number as well with smaller
size of slots in each circle.
Figure 2: Fractal of entrenches.
4.3 Koch Snowflake Fracta
This design is another pattern of fractals, and is well
mentioned by many researchers around the world. For
instance, it takes its shape primarily from the
microscopic-scale design of a snowflake unit.
The design starts out as a solid equilateral triangle
like the Sierpinski gasket, as illustrated in Figure 2.
Nevertheless, unlike the Sierpinski gasket that is
formed by downgrading the size of the triangles from
the original structure, the Koch snowflake is
accumulated by adding downgrading triangles into
the structure in an iterative style, as in Figure 3
(Douglas et al., 2003).
Figure 3: Koch snowflake fractal iterations.
4.4 Self-similarity Fractals
It refers to objects that contain smaller copies or
duplicates of itself at arbitrary scales. Figure 4 shows
an example of a natural self-similarity fractal. Such
fractal can further be divided into three items of self-
similarity fractals.
4.4.1 Exact Self-similarity Fractal
The fractal is the same at diverse balances. Such
fractal is the sturdiest kind of the self-similarity type.
4.4.2 Quasi-self-similarity Fractal
The fractal is about to be alike at diverse balances.
This one is a fewer specific system of self-similarity
type. Such fractals comprehend minor duplicates of
the whole fractal in slanted forms.
4.4.3 Statistical Self-similarity
It is the weakest type of self-similarity; hence, this
fractal has computational or statistical measurements
that are preserved across scales. However, most
famous definitions of fractals imply some meaning of
statistical self-similarity (a dimension of a fractal is a
numerical measurement that is kept across scales).
Further, random fractals are kind of fractals that are
computationally or statistically self-similar, but
neither quasi-self-similar nor exactly self-similar
(Nicoletta, 2013).
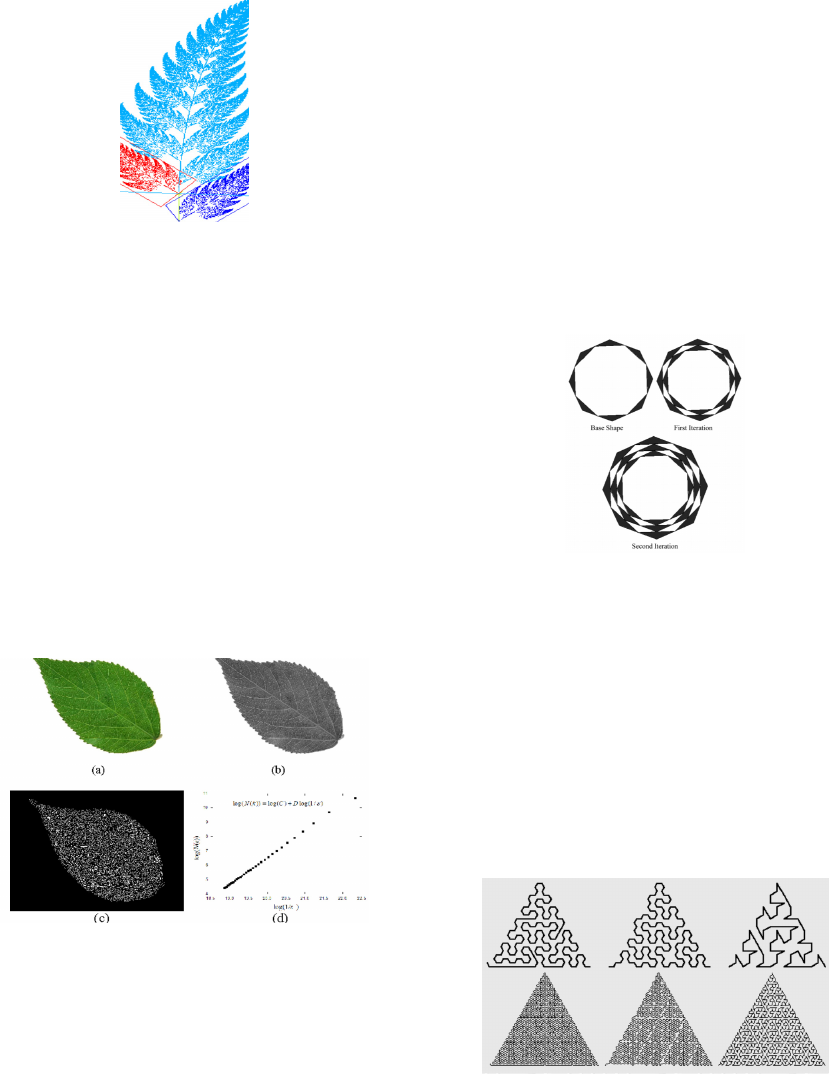
Figure 4: Barnsley fern exhibiting self-similarity fractal
behavior.
4.5 Pixel-covering Method Fractal
It is useful to compute the fractal dimensions of
objects, such as leaves, based on many plant species
acquired from several places for the sake of plant
classification and identification. Therefore, both
contour fractal dimension and the contour & nervure
fractal dimension can distinguish leaves between
different types effectively despite a little deficiencies.
The process works by adding the fractal dimension of
nervure details into the whole classification system
that can determine leaves more robustly than that of
contour and contour & nervure. Figure 5 depicts a
classification process by using pixel-covering method
(Wei et al., 2009).
Figure 5: A classification process by pixel-covering
method.
4.6 Fractals for Geo-chemical
Exploration Data of a Geological
Area
In this type of fractals, multi-fractal method is carried
out to process up to 1:200000 stream sediment geo-
chemical examination data of a geographical area.
Fractal dimension characteristics of a number of
elements connected with minerals are gained based
on (C-A) fractal technique, in addition to diverse geo-
chemical anomaly stages and components mixtures
(Shili Liao et al., 2012).
4.7 Growing-to-the-inside Fractals
This technique in generating fractals was proposed by
some researchers. Abolfazl Azari proposed an
example of such design (Abolfazl, 2011). The design
takes the shape of octagonal arrays formed by placing
elements in an equilateral triangular net. Hence, these
arrays can be viewed as involving of a single item at
the center, bounded by several concentric eight
element circular arrays. Figure 6 depicts the iterations
of the proposed design of such fractal.
Figure 6: The iterations of the proposed fractal by
(Abolfazl, 2011).
4.8 Space Filling Techniques as
Fractals
Space filling techniques can serve as a method of
generating fractals. They take the merit of packing
extra lines and curves as the rank of the technique gets
higher. For instance, the most famous techniques to fill
spaces are Hilbert, Peano, Moore, Dragon, Gosper,
Koch techniques. Figure 7 shows three patterns that fill
spaces in a deterministic mathematical style.
Figure 7: Three curves for filling spaces as fractals
(teachout).
4.9 Three-dimensional Fractals
They exist in nature and mathematics and cover many
aspects of fractalism in nature and artificial

computations. Most natural fractals are, somehow, in
the form of 3D pattern; hence, they mostly change
their way of spreading in more than one plane.
Moreover, some examples of three-dimensional
fractals are DNA, neurons, natural or artificial
surfaces, soil, clouds, etc. Figure 8 exposes an
example of a natural three-dimensional fractal.
Figure 8: A 3-D fractal shape.
4.10 Fractals of Multi-scroll Chaotic
Attractors
Attractors are sets of numerical values of a system
that goes to evolve, though they sometimes look
complicated and random. In fractals, sets of multi-
scroll chaotic attractors are hard to simulate and to be
put in a mathematical model to represent the fractal
structure. However, Lu Chen attractor and the
modified Chua chaotic attractor are examples of
modeling attractors and are applicable to comprehend
the fractal implementation. Figure 9 shows an
example of a multi-scroll chaotic attractor fractal.
Figure 9: Fractal of multi-scroll chaotic attractors.
5 MATHEMATICAL
REPRESENTATION OF
FRACTAL INITIATION
Fractals have wide scopes of mathematical
characterization that fill a specific boundary of
occupation. Further, large number of fractals are
deterministic, i.e. they commonly can be predicted by
utilizing mathematical and logical formulas. In
addition, it is likely to have fractals that are hard or
impossible to obtain a computational formula of
representation. In such a case many naturally built
fractal shapes, such as coral reefs, trees, landscapes,
etc. As indicated by many researchers around the
world, it is not completely known the precise reason
that explains the mathematical patterning of fractals
in nature. The following lists some mathematical
patterns of fractal characterization.
5.1 Fractal Interpolation
Chih-Chin Huang, Shu-Chen Cheng, and Yueh Min
Huang in the refrence (Chih-Chin et al., 2010)
investigated a new algorithm to generate a new
interpolation scheme. Such an algorithm is helpful in
the techniques concerning generating and forecasting
fractal numbers out of a few numbers. Figure 10
shows an example of fractal interpolation of images.
Figure 10: Fractal interpolation of images (Pantelis et al.,
2007).
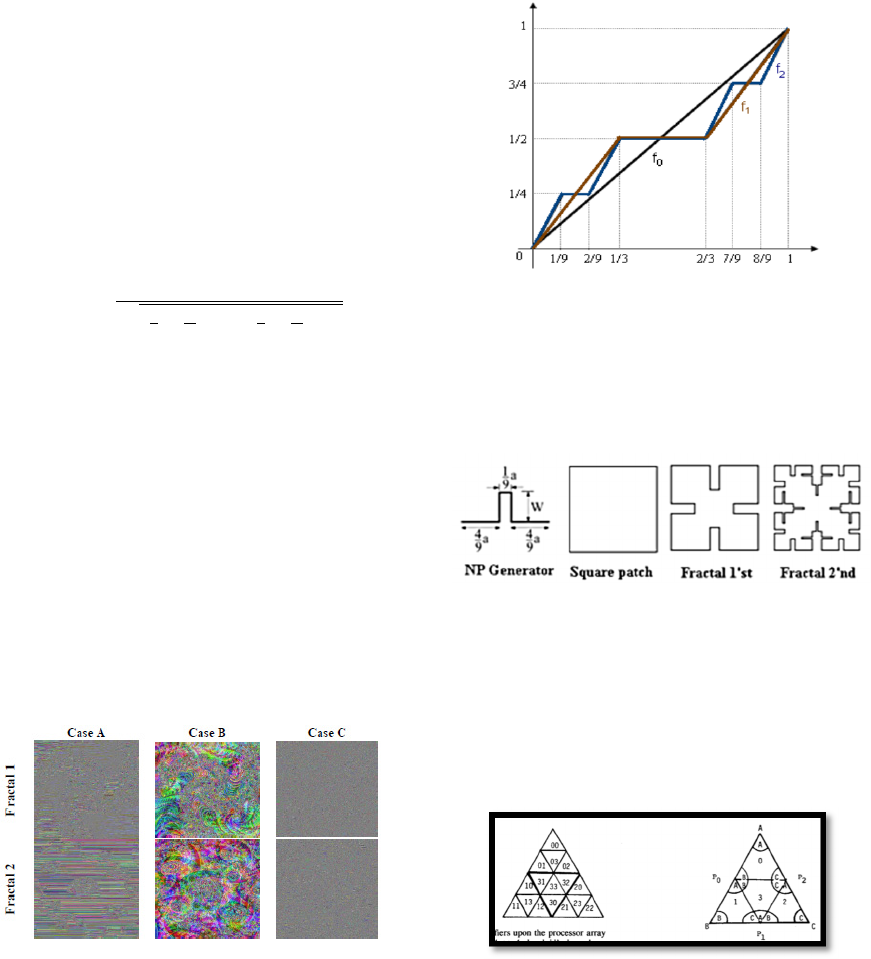
5.2 Iterated Function Systems
Iterated function systems, or (IFS), represent a very
various technique for properly generating a wide-
ranging useful fractal structures. Such iterated
function systems stand on the application of a series
of affine transformations as in figure 11 (Douglas et
al., 2003).
Figure 11: the construction of the standard Koch curve via
an iterated function system (IFS) approach.
5.3 Circulation of Fractals
As an example of such technique is what appears
earlier in this article in the item [Fractal by
entrenches]. When the designer used multi-circles of
entrenches (18 circle per rotation) that have the same
characteristics with different scales.
5.4 Super-formula
Johan Gielies presented this formula. Such a formula
mostly describes the natural fractal phenomenon
(Nicoletta, 2013). The following equation describes
the general formula of this theory.
𝑟𝑓∅
∅
∅
5.5 Logarithmic Fractals
This technique is mostly useful in the fractals that
relate to natural organs. Figure 5 represents a vital
organ having such technique (Wei et al., 2009).
5.6 Pseudo Random Key-stream
Generator
Pseudo random number generators have played a
critical research point due to the demand on quality-
encoded content that is essential in all of the structure
of the communication networks. Such technique has
many examples and can be found in variety of
research papers as in figure 12.
Figure 12: Example of Pseudo Random Keystream
Generator using Fractals (Sherif et al., 2013).
5.7 Space filling Curvature Formulas
There are many formulas to represent such
curvatures, such as Cantor function, Tietze extension
theorem, Euclidean metric, Lindenmayer system, L-
System, segment division, Weierstrass function, other
deterministic and un-deterministic methods. Figure
13 shows an example of Cantor function that has a
fractal extension in its higher order formulas.
Figure 13: A graph of Iterative Construction of Cantor
function.
5.8 NP Generator Model
It includes iterating a Narrow Pulse within a specific
shape as in figure 14.
Figure 14: A model of NP generator for a square patch
(Mahatthanajatuphat et al., 2007).
5.9 Triangular Sub-divisions
This kind of fractal formation may exist in fractal-
related computer processors and arrays (Wainer,
1988). An example of such generator can be shown in
figure 15.
Figure 15: A sub-divisions method process (Wainer, 1988).
5.10 Multi-scroll Chaotic Attractor
Generator
Many models represent such structures and have an
evolving approach, resembling Lu Chen and the
modified Chua chaotic attractors. Figure 16 shows an
example of a system of fractal processes and
transformation Φ (Bouallegue, 2011).

Figure 16: System of fractal processes and transformation
as an example of Multi-scroll chaotic attractor generator.
5.11 Random Iteration Algorithm
The preliminary set is a single point and at each point
of iteration, only one of the essential affine
transformations is used to compute the following
level (Ankit et al., 2014). Moreover, Hsuan T. Chang
presented a group of decoded images by the random
iteration algorithm as in figure 17 (Hsuan, 2001).
Figure 17: Decoded images of fractals by the random
iteration algorithm: (a) Sierpin´ski triangle, (b) fern, (c)
castle, and (d) snowflake.
5.12 Stochastic Fractal Search (SFS)
Algorithm
Such algorithm is considered to be a development of
Evolutionary Algorithms (EAs), and it uses the
diffusion merit that is seen frequently in random
fractals. The particles in such algorithm discover the
searching space more powerfully and is used
optimization processes (Salimi, 2015).
6 FRACTAL-GENERATING
SOFTWARE
Fractal generation software represents every kind of
software of graphics generating images of fractals.
However, there are numerous programs of fractal
generation obtainable, together open and profitable.
Mobile applications are accessible to play with fractal
designs. Various programmers generate fractal
software for their interest due to the innovation and
due to the challenges in comprehending the related
mathematical problems. Therefore, generating
fractals has directed many large difficulties and
projects for pure mathematics.
Mainly, there are two key approaches of two-
dimensional generation of fractals. First of which is
to conduct a process of iteration to simplify
calculations by recursion generation (Daniel, 2017).
On the other hand, the other chief approach is with
Iterated-Function-Systems (IFS) that consist of an
amount of affine alterations. In method number one,
every pixel within fractal images is assessed based on
a function and, at that time, colored, beforehand the
similar procedure is conducted to the following pixel.
Hence, the previous technique characterizes the
traditional stochastic method, whereas the second
builds a linear model of fractals. Utilizing recursion
have permitted program operators to generate
complicated images over modest direction [19-21].
• Chaotica:
A commercialized fractal art software
and renderer prolonging flam3 as well as
Apophysis function.
• Apophysis:
An open-source fractal flame
software intended for Microsoft Windows and
Macintosh.
• Fractint:
Free software to display numerous
types of fractals. The software was created on
MS-DOS, after that transported to the Atari ST,
Macintosh and Linux.
• Electric Sheep:
An open-source spread screen
saving software, and was established by S.
Draves.
• Kalles Fraktaler:
A free Windows built fractal
zooming program.
• Milkdrop:
A hardware with accelerated music
visualizing plugin intended for Winamp that was
initially advanced by R. Geiss.
• XaoS:
A fractal zooming software with
interaction.
• Fyre:
An open source cross-platform apparatus
intended for creating images centered about
histograms of repeated chaotic functions.

• OpenPlaG: It generates fractal by sketching
modest functions and is PHP based.
• MojoWorld Generator: It was a commercial
fractal landscape initiator intended for Windows.
• Sterling: Freeware fractal generator software
inscribed with C language.
• Picogen: A freeware open source cross platform
terrain initiator written in C++.
• Terragen: A generator of fractal terrain, which
can handle animations in Mac OS X and
Windows.
• Wolfram Mathematica: Dedicated for many
computer science software and for creating
fractal images as well.
• Ultra Fractal: A rendering generator for fractals
in Mac OS X and Windows.
7 CONCLUSION
In this research-reviewing article, the authors give a
summarized idea of collecting what many researchers
have been investigating in the field of fractals. During
decades, the concept of understanding fractals in
nature has led to employ this idea in the industrialized
and artificial forms. Backed from its history, area of
fractals is developing in terms of classification,
benefits, future employment, further understanding
and relation with life origins. It is expected, in
addition, that such field in researching fractals and
utilizing it in modern-life employment would
enhance the efforts in finding new algorithms to
expand the atmosphere that fractals deploy.
Furthermore, there is a fact that utilizing fractals in
the fields of microwave and antenna engineering has
practically occupied the most complicated and
expanded effort by engineers and researchers through
theory, simulation, and prototyping.
For the sake of future direction, fractal generating
techniques will develop further to comprehend the
increasing demands in variety of applications; hence,
the incoming trend is seeking for more compact and
practical designs and concepts.
REFERENCES
Mandelbrot, Benoit B. “The fractal geometry of nature,"
Macmillan, 1983.
Paul Bourke, “An Introduction to Fractals," 1991.
Douglas H. Werner and Suman Gangul, “An Overview of
Fractal Antenna Engineering Research," IEEE
Antennas and Propagation Magazine. Vol. 45, NO. 1,
p.p. 38 – 57, February 2003.
Nicoletta Sala, “Fractal geometry and super formula to
model natural shapes," IJRRAS, Vol.16, Issue 4, p.p. 78
– 92, Oct. 2013.
Wei Jiang, Cui-Cui Ji, and Hua Jun Zhu, “Fractal Study on
Plant Classification and Identification," International
Workshop on Chaos-Fractals Theories and
Applications, Shenyang, China, p.p. 434 – 438, 6-8
Nov. 2009.
Shili Liao, Shouyu Chen, and Xiaohu Deng, “Application
of Fractal Approach to Process Geochemical
Exploration Data of Baiyin Area, Gansu Province,"
Fifth International Workshop on Chaos-fractals
Theories and Applications, Dalian, China, p.p. 303 –
307, 18 – 21 Oct. 2012.
Abolfazl Azari, “A New Super Wideband Fractal
Microstrip Antenna," IEEE Transactions on Antennas
and Propagation, Vol. 59, No. 5, p.p. 1724 – 1727, May
2011. Website: http://teachout1.net/village/copyright.
html/Gary, teachout
Chih-Chin Huanga, Shu-Chen Chengb, and Yueh M.
Huanga, “The Design of a Fractal-based Number
Generator," International Workshop on Chaos-Fractal
Theory and its Applications, Kunming, China, p.p. 435
– 439, Oct. 29 – 31, 2010.
Pantelis Bouboulis, Pantelis Bouboulis, “A general
construction of fractal interpolation Functions on grids
of IRn," European Journal of Applied Mathematics,
18:449-476, August 2007.
Sherif H. AbdElHaleem, Ahmed G. Radwan and Salwa K.
Abd-El-Hafiz, “Design of Pseudo Random Keystream
Generator Using Fractals," IEEE 20th International
Conference on Electronics, Circuits, and Systems
(ICECS), United Arab Emirates, p.p. 887 – 880, Dec.
2013.
Mahatthanajatuphat, Chatree, and Prayoot Akkaraekthalin,
“Fractal Array Antennas with NP Generator Model," In
ISAP, 1202-5. Japan, 2007.
M.Wainer, “Generating Fractal-Like Surfaces on General
Purpose Mesh-Connected Computers," IEEE
Transactions on computers, Vol. 37, No. 7, p.p. 882 –
886, July 1988.
Bouallegue, K. “Generation of Multi-Scroll Chaotic
Attractors from Fractal and Multi-Fractal Processes," In
2011 Fourth International Workshop on Chaos-Fractals
Theories and Applications, p.p. 398 – 402, 2011.
https://doi.org/10.1109/IWCFTA.2011.87.
Ankit Garg, Akshat Agrawal and Ashish Negi, “A Review
on Natural Phenomenon of Fractal Geometry,"
International Journal of Computer Applications (0975 –
8887), p.p. 1 – 7, Vol. 86, No. 4, January 2014.
Hsuan T. Chang, “Relocation, scaling, and quantization
effects on fractal images," Optical Engineering, 40 (6),
p.p. 941 – 951, June 2001.
Salimi, Hamid. “Stochastic Fractal Search: A Powerful
Metaheuristic Algorithm." Knowledge-Based Systems
75 (February 1, 2015): 1 – 18. https://doi.org/10.1016/
j.knosys.2014.07.025.
Daniel Shi_man. "Chapter 8. Fractals". The Nature of Code.
Retrieved 5 March 2017.
Chen, Yan Qui, and Guoan Bi. “3-D IFS Fractals as Real-
Time Graphics Model," Computers & Graphics,
Computer Graphics in China, 21, no. 3 (May 1, 1997):
367 – 70. https://doi.org/10.1016/S0097-8493(97)000
14-9.
Nikiel, Slawomir S. “True-Colour Images and Iterated
Function Systems." Computers & Graphics 22, no. 5
(October 1, 1998): 635-40. https://doi.org/10.1016/S0
097-8493(98)00072-7.
Peitgen, Heinz-Otto; Peter Richter (1986). The Beauty of
Fractals. Springer-Verlag. p. 2. ISBN 978-0883859711.
Retrieved 7 May 2017.
