Energy and Latency Minimization in a Mobile Edge Computing System
Mohamed El Ghmary
1 a
, Youssef Hmimz
1 b
, Tarik Chanyour
1 c
and Mohammed Ouc¸amah Cherkaoui Malki
1 d
1
Department of Computer Sciences, SidiMohamed Ben Abdellah University, FSDM, Fez, Morocco
Keywords:
Mobile edge computing, computation offloading, energy, processing time, bi-objective optimization, heuristic,
multi-task.
Abstract:
Mobile Edge Computing (MEC) extends the Cloud Computing paradigm to the edge of the network, thus
enabling a new breed of applications and services; hence it is considered as a promising technique to meet the
demands of computing intensive and delay sensitive applications. This article describes the value for a trade
off between processing time and energy in a MEC environment. The optimization problem formulated takes
into account both the processing time and the dedicated energy capacity. To solve this problem we proposed
a heuristic solution scheme. To evaluate our solution, we performed a comparative study with a brute force
search solution. The results obtained are entirely very satisfactory.
1 INTRODUCTION
Cloud computing (CC) invaded and promised a better
way to improve server efficiency, shrink infrastruc-
ture footprint and allowed the use of centralized stor-
age and made computing units available and on de-
mand for the end user. However, with the rapid grow-
ing amount of data caused by the massive diffusion of
Internet of Things (IoT), which refers to the billions
of physical devices with limited computing capacities
that are connected to the internet and need a real-time
data processing (Bilal, 2018), CC is no longer consid-
ered as a suitable solution. Therefore, Mobile Cloud
Computing (MCC) was introduced as a potential so-
lution to these limitations (Dinh et al., 2013) at first,
but the data processing and storage were still in the
Clouds which leads us to a new concept called Fog
computing where the data remains distributed among
the Fog nodes (Al-Qamash et al., 2018) hence the per-
formance is still limited because of its dependence on
the Cloud.
Motivated by the above challenges and the need to
make a move towards the next cellular network gener-
ation 5G that aspires to achieve substantial improve-
ment on quality of service (Hassan et al., 2019) for
IoT devices users, Mobile Edge Computing appeared
a
https://orcid.org/0000-0001-5970-481X
b
https://orcid.org/0000-0001-7625-2106
c
https://orcid.org/0000-0002-7676-0749
d
https://orcid.org/0000-0001-8811-9820
with capabilities such as storage and computational
capacities that offer low latency, proximity since they
are located at the Edge of the network which means
within the Radio Access Network (RAN) and base
stations (Hassan et al., 2019), location awareness and
higher bandwidth (Sabella et al., 2016). However, the
main challenge is that the IoT will connect a large
number of heterogeneous devices with limited local
computing resources, which will require a strategy
that enables these devices to offload their intensive
tasks to other servers. Therefore, mobile edge server
should be able to make an effective offloading deci-
sion.
The crucial part in computation offloading is de-
ciding whether to offload or not, according to (Hmimz
et al., 2019),(El Ghmary et al., 2020) we can find
three possibilities: local execution, partial offloading
and full offloading. In this regard, many studies have
proposed a variety of solutions in order to reduce to-
tal energy consumption in a single device multi-task
environment. The authors (Li, 2018) compared an
algorithm that selects tasks with large data size and
heavy calculation burden to another algorithm that re-
lies on a probabilistic technique. Meanwhile in a sin-
gle server, multi-user environment, (You et al., 2016)
investigated the energy efficiency using a centralized
method that makes a binary offloading decision for
each mobile where users will perform the offloading
with high or low priorities according to a given thresh-
old. However,(Rahati-Quchani et al., 2019) consider

optimizing energy consumption by offloading mobile
users with only a better utility. Finally, considering
a multi-server, multi-user environment, (Huang et al.,
2019) and (Lyu et al., 2016) used a decentralized as-
signment mechanism where the MEC aims to select
mobile devices with better benefits to minimize en-
ergy consumption, and (Xu et al., 2019) employed
the enumerating algorithm and branch-and-bound to
get the optimal decision that minimizes energy con-
sumption, while (Chen, 2014) proposed a decentral-
ized computation offloading game theory that allows
users to make the offloading decision assuming that
they know how to keep the system balanced.
Many studies (Li, 2018), (Lyu et al., 2016),
(Rahati-Quchani et al., 2019), (Xu et al., 2019) and
(Chen, 2014) neglected the response time while send-
ing the output from the MEC to the Mobile device
assuming that the output is much smaller than the in-
put, hence the return time has little effect on the to-
tal time consumption. In a single device multi-task
environment, we are going to consider the local exe-
cution time, the required time to send the input data
to the MEC, the execution time on the server and fi-
nally the response time to send the output to the end
user in order to reduce the global time of the offload-
ing process. In this paper, we consider a single smart
mobile device multi-task offloading environment, be-
sides, we introduce the available energy of the smart
mobile device (SMD) as a constraint. Moreover, we
introduced the MEC Server’s frequency and the SMD
frequency as a decision variable in our optimization
problem. Therefore, we can extend the battery life-
time of the SMD and reduce the processing time of
its tasks.
The rest of this paper is structured as follows: Sec-
tion 2 gives the system model. The optimization prob-
lem formulation and its solution are discussed in Sec-
tions 3, 4 and 5. Then, the simulation results are dis-
cussed in Section 6. And finally, we conclude this
paper in section 7.
2 SYSTEM MODEL
In this system model, we will consider a single user
scenario where a SMD has N independent tasks that
are executed locally or offloaded to the MEC Server
for computation.
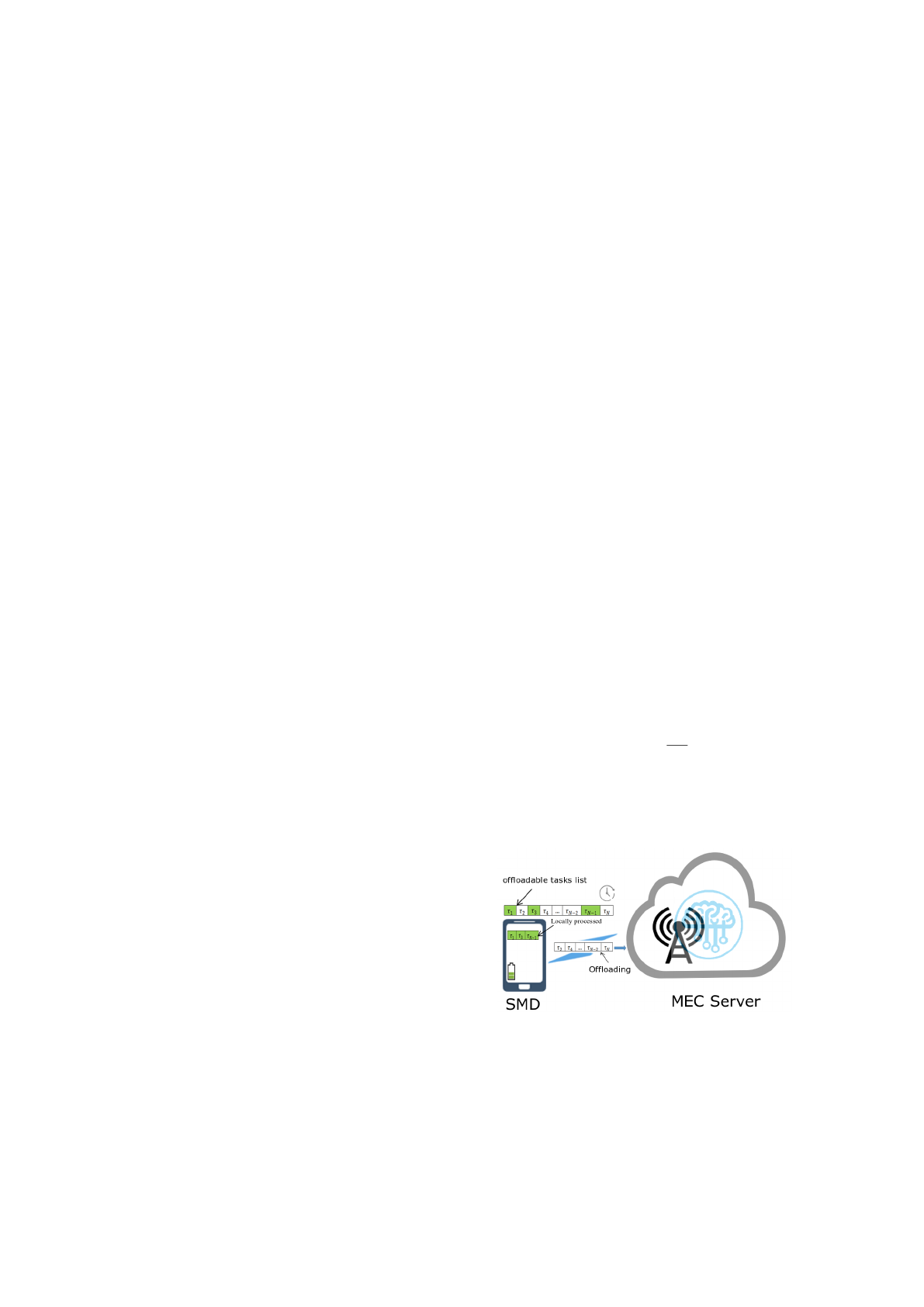
Figure 1 shows a general network topology that
connects a SMD to a MEC Server. This SMD intends
to offload a list of independent tasks by the means of
an Edge Access Point (EAP). In this paper, we aim
to examine the behavior of the offloading process in a
MEC environment, while we optimize computing re-
sources disposable at the SMD as well as at the MEC
Server. Especially, the energy which can be taken by
the SMD for tasks execution is restricted. Moreover,
in the context of offloading, some parts of a computa-
tionally intensive application are splitted into several
mutually independent offloadable tasks (Chun et al.,
2011). Consequently, depending on the free compu-
tational and radio resources, some tasks are selected
from the tasks list to be offloaded to the MEC Server
for processing. The remaining tasks are handled lo-
cally by the MDS itself. The completion of all tasks
must take place within the application deadline. In ad-
dition, we assume that the SMD can simultaneously
perform computations and wireless transmission.
Let note: τ ,
{
τ
1
,τ
2
,...,τ
N
}
a list of N indepen-
dent tasks, these tasks are assumed heavy and delay
sensitive. In addition, these tasks can be executed by
the SMD or by the MEC Server. Besides, the pro-
cessing time of the task τ
i
cannot exceed a required
maximum latency T
sup
i
and the overall energy for the
execution of all the tasks locally must be less than
the quantity of energy tolorated E
sup
. Also, Every
task represents an atomic input data that cannot be di-
vided into sub-tasks and it is mainly characterized by
three parameters τ
i
,

Γ
i
,d
i
,T
sup
i

where γ
i
[cycles]
identifies the workload needed to accomplish the ex-
ecution of this task, d
i
[bits] identifies the input data
size and program codes to deliver from the SMD to
the MEC Server. and T
sup
i
refers to the maximum la-
tency required for this task. In addition, In line with
Shannon equation, the transmission rate(bits/s) can be
expressed in the following formula as equation ( 1).
r = B log

1 +
p
T
g
BN
0

(1)
where B stands for upstream bandwidth, p
T
is the
transmission power required by SMD to offload the
input data to MEC Server, g is its channel gain, and
N
0
is the noise power spectral density. The execu-
Figure 1: System model illustration
tion decision for a task τ
i
either locally by SMD or
by offloading to the MEC Server is denoted y
i
where
y
i
∈ {0;1}. y
i
= 1 indicates that the SMD has to of-
fload τ
i
to the MEC Server, and y
i
= 0 indicates that

τ
i
is locally executed.
If the task τ
i
executed locally by the SMD, the time of
its local execution is: t
smd
i
=
γ
i
f
smd
[seconds]. And for
all tasks we have:
t
smd
=
N
∑
i=1
(1 − y
i
)
γ
i
f
smd
[seconds], (2)
where f
smd
stands for CPU local frequency.
The energy consumption of its local execution is
given by: e
smd
i
= k
smd
f
2
smd
γ
i
[J]. Consequently, the to-
tal energy consumption for all tasks locally executed
by the SMD is given by:
e
smd
=
∑
N
i=1
e
smd
i
(1 − y
i
) = k
smd
f
2
smd
∑
N
i=1
γ
i
(1 − y
i
)[J].
(3)
If task τ
i
is offloaded to the MEC Server, The total
computing time is: t
mec
i
= t
C
i
+ t
S
i
+ t
R
i
, where t
C
i
is
the time to offload the task to the MEC Server, and
it is given by: t
C
i
=
d
i
r
[seconds].t
S
i
is the time to pro-
cess the task τ
i
at the MEC Server, and it is given
by: t
S
i
=
γ
i
f
mec
+t
R
i
[seconds]. t
R
i
is the time to send the
result out from the MEC Server. We ignore this re-
sponse time and its energy consumption as adopted by
(Zhang et al., 2016) since the output data size is usu-
ally ignored compared to the input data size. Hence,
for the τ
i
task: t
mec
i
= y
i

d
i
r
+
γ
i
f
mec

[seconds]. And
for all tasks, we have:
t
mec
=
∑
N
i=1
y
i

d
i
r
+
γ
i
f
mec

[seconds],
(4)
where f
mec
stands for MEC Server frequency.
Thus, the communication energy can be formu-
lated as: e
C
i
=
p
T
d
i
r
[J]. And for all tasks, we have e
C
=
p
T
∑
N
i=1
y
i
d
i
r
[J]. Similarly, energy consumption (Chen
et al., 2015) at the MEC Server while executing τ
i
is
given by: e
mec
i
= k
mec
f
2
mec
γ
i
[J]. The total energy con-
sumption for all tasks executed by the MEC Server is
given by:
e
mec
= k
mec
f
2
mec
N
∑
i=1
γ
i
y
i
[J].
(5)
Finally, given the offloading decision set Y ,
{
x
1
,x
2
,...,x
N
}
for all tasks, the SMD execution fre-
quency f
smd
and the MEC Server execution frequency
f
mec
, the total processing time for all tasks can be for-
mulated as:
T (Y, f
smd
, f
mec
) =
∑
N
i=1
γ
i
−
∑
N
i=1
γ
i
y
i
f
smd
+
∑
N
i=1
d
i
y
i
r
+
∑
N
i=1
γ
i
y
i
f
mec
.
(6)
Similarly,the total energy consumption for all tasks
can be formulated as:
E (Y, f
smd
, f
mec
) = K
∑
N
i=1
γ
i
y
i
+ k
smd
f
2
smd
∑
N
i=1
γ
i
+
p
T
∑
N
i=1
y
i
d
i
r
,
(7)
where K = k
mec
f
2
mec
− k
smd
f
2
smd
.
3 PROBLEM FORMULATION
Now, we present in this section our optimization prob-
lem formulation that plans to minimize the total en-
ergy consumption and total processing time in the of-
floading process, while maintaining the battery life-
time. The obtained problem is written as follows:
CT E(Y, f
smd
, f
mec
) =
α
T
sup
T (Y, f
smd
, f
mec
) +
β
E
sup
E(Y, f
smd
, f
mec
)
(8)
Where α and β are the weights given to the two objec-
tives, respectively, with α + β = 1. The role of E
sup
and T
sup
= max
i

T
sup
i

, is to eliminate the units of
energy and of processing time and to normalize them
in the objective function.
P
1
:



































min
{
CT E(Y, f
smd
, f
mec
)
}
s.t.
(C
1.1
) y
i
∈
{
0;1
}
; i ∈ [[1; N]]
(C
1.2
) F
in f
smd
≤ f
smd
≤ F
sup
smd
(C
1.3
) 0 < f
mec
≤ F
S
(C
1.4
)
(1−y
i
)
∑
i
k=1
γ
k
(1−x
k
)
f
smd
≤ T
sup
i
; i ∈ [[1; N]]
(C
1.5
) y
i
∑
i
k=1
x
k
(
d
k
r
+
γ
k
f
s
) ≤ T
sup
i
; i ∈ [[1; N]]
(C
1.6
) k
smd
f
2
smd
∑
N
i=1
γ
i
(1 − y
i
) +
p
T
r
∑
N
i=1
y
i
d
i
≤ E
sup
In this paper, each task can be either executed locally
by the SMD or offloaded to the MEC Server. So, ev-
ery feasible offloading decision solution has to satisfy
the constraints below:
The first constraint (C
1.1
) refers to the offloading de-
cision variable y
i
for task τ
i
which equals 0 or 1. The
second constraint (C
1.2
) indicates that the allocated
variable local frequency f
smd
belongs to a priori fix
interval given by [F
in f
smd
,F
sup
smd
]. Similarly, the allocated
variable remote MEC Server frequency f
mec
belongs
to the interval ]0,F
S
] in the third constraint (C
1.3
). The
fourth constraint (C
1.4
) shows that the execution time
of all decided local tasks must be less than the given
latency requirement T
sup
i
. In the same way, in the fifth
constraint (C
1.5
), the offloading time of all decided re-
mote tasks must satisfy the same latency requirement
T
sup
i
. The final constraint (C
1.6
) is important espe-
cially if the SMD’s battery power is critical. It im-
poses that the local execution energy must not exceed
the specified amount E
sup
.
4 PROBLEM RESOLUTION
In this section, we present how we could resolve the
obtained optimization problem.

4.1 Problem Decomposition
In our suggested model, the offloading decision set
for all the tasks is denoted Y. Let declare the set that
contains the offloadable tasks’ identifiers:
Y
0
= {i ∈ Y/y
i
= 0} and Y
1
= {i ∈ Y/y
i
= 1}.
We define: Γ
i
=
∑
i
k=1
γ
k
, Γ
1
i
=
∑
i
k=1
x
k
γ
k
, Γ =
Γ
N
− Γ
N
1
, D
i
=
∑
i
k=1
d
k
and D
1
i
=
∑
i
k=1
x
k
d
k
.
Given the decision set Y
0
, constraint (C
1.4
) for a
local task can be reformulated as
Γ
i
−Γ
1
i
T
sup
i
≤ f
smd
;
∀i ∈ [[1; N]], that is max
i
n
Γ
i
−Γ
1
i
T
sup
i
o
≤ f
smd
. The con-
straint (C
1.5
) for an offloadable task implies
D
1
i
r
+
Γ
1
i
f
mec
≤ T
sup
i
; ∀i ∈ [[1;N]]. Then
D
1
i
r
and
Γ
1
i
f
mec
must
be strictly less than T
sup
i
; ∀i ∈ [[1; N]]; in particu-
lar min
i
n
T
sup
i
−
D
1
i
r
o
> 0. In that case, the con-
straint (C
1.5
) can be reformulated as:
Γ
1
i
T
sup
i
−
D
1
i
r
≤
f
mec
;i ∈ [[i; N]]. Eventually, it sums to a constraint:
max
i
n
Γ
1
i
T
sup
i
−
D
1
i
r
o
≤ f
mec
. The constraint (C
1.6
) can
be written as: f
smd
≤
q
E
sup
k
smd
Γ
N
−Γ
1
N
. For more facili-
tation of use, we note: f
−
smd
= max
i
n
Γ
i
−Γ
1
i
T
sup
i
o
, f
+
smd
=
q
E
sup
k
smd
(
Γ
N
−Γ
1
N
)
and f
−
mec
= max
i
n
Γ
1
i
T
sup
i
−
D
1
i
r
o
. Hence,
for a given offloading decision set Y, Considering
the continuous variables f
smd
and f
mec
, P1 is an op-
timization problem with continuous multivariables.
The objective function CT E(Y, f
smd
, f
mec
) can be di-
vided into two independent functions: CT E
1
( f
smd
)
and CT E
2
( f
mec
) where:
CT E
1
( f
smd
) = Γ
α
T
sup
f
smd
+
βk
smd
f
2
smd
E
sup
!
(9)
CT E
2
( f
mec
) = Γ
N
1

α
T
sup
f
mec
+
βk
mec
f
2
mec
E
sup

+
D
N
1
r

α
T
sup
+
βp
T
E
sup

.
(10)
P
2.1
(Y) :







min{CT E
1
( f
smd
)}
s.t.
(C
2.1.1
) F
in f
smd
≤ f
smd
≤ F
sup
smd
(C
2.1.2
) f
−
smd
≤ f
smd
≤ f
+
smd
P
2.2
(Y) :



min{CT E
2
( f
mec
)}
s.t.
(C
2.2.1
) f
−
mec
≤ f
mec
≤ F
S
4.2 Problems Resolution
For the P2.1 problem, variation study of the objec-
tive function CT E
1
( f
smd
) shows that it has an optimal
minimum value at the point
3
q
αE
sup
2βk
smd
T
sup
i
without con-
sidering constraints (C
2.1.1
) and (C
2.1.2
). Then, the
optimum f
∗
smd
of the CT E
1
( f
smd
) function given by:
f
∗
smd
=























0 if Y = Y
1
/
0 if E
sup
≤
p
T
D
N
1
r
or f
−
smd
> F
sup
smd
or f
+
smd
< F
in f
smd
or f
−
smd
> f
+
smd
f
−
smd
if
3
q
αE
sup
2βk
smd
T
sup
< f
−
smd
f
+
smd
if
3
q
αE
sup
2βk
smd
T
sup
> f
+
smd
3
q
αE
sup
2βk
smd
T
sup
otherwise
(11)
For the P2.2 problem, variation study of the objec-
tive function CT E
2
( f
mec
) shows that it has an optimal
minimum value at the point
3
q
αE
sup
2βk
smd
T
sup
i
without con-
sidering constraint (C
2.2.1
). Therefore, the optimum
f
∗
mec
of the CT E
2
( f
mec
) function given by:
f
∗
mec
=

















0 if Y = Y
0
/
0 if f
−
mec
> F
S
or
D
N
1
r
> T
sup
f
−
mec
if
3
q
αE
sup
2βk
mec
T
sup
< f
−
mec
F
S
if
3
q
αE
sup
2βk
mec
T
sup
> F
S
3
q
αE
sup
2βk
mec
T
sup
otherwise
(12)
5 PROPOSED SOLUTIONS
Next, the problem relies on identifying the optimal
offloading decision set Y that gives the optimal energy
consumption and the optimal processing time. Yet, to
iterate over all possible combinations of a set of N
binary variables, the time complexity is exponential.
However, this is not practical for large values of N.
To solve this problem, we propose a low complexity
approximate algorithm.
5.1 Exact Solution
For a comparison purpose, we introduce the Exhaus-
tive Search Offloading (ESO) method for feasible
small values of N. This method explores all cases of
offloading decisions and saves the one with the mini-
mum trade off between energy and processing time as
well as its completion time.
5.2 Heuristic Solution
In this section, we present our proposed solution,
which we denote Simulated Annealing Offloading
(SAO), we utilize a Simulated Annealing based
heuristic (Fan et al., 2013) and (Chen et al., 2017).
We begin by a random offloading decision state Y.
Then, for every step, some neighboring state Y
∗
of the

current state Y and probabilistically decides between
moving the system to state Y
∗
or staying in state Y. In
practice, varying a state consists of changing the deci-
sion to offload certain tasks to the MEC Server. These
probabilistic transitions eventually cause the system
to switch to lower energy states. Usually, this step
is repeated until a good compromise between energy
and processing time is reached, or until a given num-
ber of iterations is reached.
6 EVALUATION AND RESULTS
6.1 Simulation Setup
All developed C++ simulation programs were built
with GCC version 6.4.0. and run using a 2.7GHz In-
tel Core i7-2620M processor in a PC with a maximum
8GB of RAM. The reached results in this paper are av-
eraged for 100 time executions. Moreover, the basic
parameters of the simulation experiments are listed in
Table 1.
Table 1: Simulations’ parameters.
Parameter values
F
in f
smd
1MHz
F
sup
smd
60MHz
F
S
6GHz
p
T
0.1Watt
k
smd
10
−26
k
mec
10
−29
T
sup
i
[0.5,2]
E
sup
[0.6,0.8]Γk
smd
(F
sup
smd
)
2
d
i
[30,300]KB
γ
i
[60;600]MCycles
r 100KB/s
Temp
0
100
α 0.5
6.2 Evaluation
The proposed solutions solve the general problem in
two phases. The first phase consists in finding the op-
timal local frequency f
smd
as well the remote MEC
Server’s frequency f
mec
according to (11) and (12).
The second phase consists in finding an optimal com-
promise between the total energy and the overall pro-
cessing time.
For the evaluation purpose, we performed an ex-
periment to compare the performance of the opti-
mal ESO solution and the heuristic SAO solution that
solve the formulated optimization problem. We vary
the number of tasks (N) between 2 and 26. Next, we
study two metrics: total energy consumption and total
processing time.
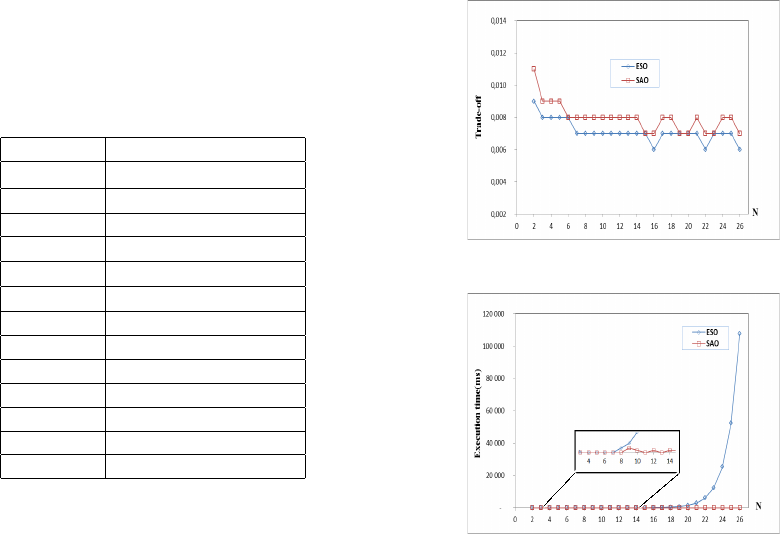
Figure 2 shows the average obtained results. It
shows a small difference between the optimal ESO
solution and the heuristic SAO solution. This differ-
ence ranges from 0.00% to 2.00%.
Figure 3 shows the average execution time of
both solutions ESO and SAO while we vary N be-
tween 2 and 26. In fact, with N = 26 SAO solution
reaches only 0, 31ms; whereas ESO solution attains
107702,35ms.
Indeed, this experiment shows that the higher the
number of tasks N is, the longer the execution time is.
Additionally, figure 3 shows an exponential variation
of the execution time for the optimal ESO solution.
It shows stable execution time for SAO with compa-
rable output in terms of the trade-off between energy
efficiency and processing time for both solutions.
Figure 2: Trade-off energy-time w.r.t. N.
Figure 3: Decision time w.r.t. N.
7 CONCLUSION
In this paper we have proposed a heuristic solution
that jointly optimizes two metrics, namely the min-
imization of the total processing time and the total
energy consumption of all the tasks. We have dealt
with a two-objective optimization problem. For that
purpose, we based ourselves on an approach of ag-
gregation of the weights which consider well spec-

ified weights for each of the two metrics in order
to achieve a compromise between them. Our solu-
tion has been validated by comparing the results ob-
tained with an accurate solution based on an exhaus-
tive search method.
REFERENCES
Al-Qamash, A., Soliman, I., Abulibdeh, R., and Saleh, M.
(2018). Cloud, fog, and edge computing: A software
engineering perspectivee. In 2018 International Con-
ference on Computer and Applications (ICCA), pages
276–284. IEEE.
Bilal, Kashif & Khalid, O. . E. A. . K. S. U. (2018). Poten-
tials, trends, and prospects in edge technologies: Fog,
cloudlet, mobile edge, and micro data centers. Com-
puter Networks, 130:94–120.
Chen, L., Wu, J., Long, X., and Zhang, Z. (2017). En-
gine: Cost effective offloading in mobile edge com-
puting with fog-cloud cooperation. arXiv preprint
arXiv:1711.01683.
Chen, X. (2014). Decentralized computation offloading
game for mobile cloud computing. IEEE Transactions
on Parallel and Distributed Systems, 26(4):974–983.
Chen, X., Jiao, L., Li, W., and Fu, X. (2015). Effi-
cient multi-user computation offloading for mobile-
edge cloud computing. IEEE/ACM Transactions on
Networking, 24(5):2795–2808.
Chun, B.-G., Ihm, S., Maniatis, P., Naik, M., and Patti, A.
(2011). Clonecloud: elastic execution between mobile
device and cloud. In Proceedings of the sixth confer-
ence on Computer systems, pages 301–314.
Dinh, H. T., Lee, C., Niyato, D., and Wang, P. (2013). A
survey of mobile cloud computing: architecture, ap-
plications, and approaches. Wireless communications
and mobile computing, 13(18):1587–1611.
El Ghmary, M., Chanyour, T., Hmimz, Y., and Malki,
M. O. C. (2020). Processing time and computing
resources optimization in a mobile edge computing
node. In Embedded Systems and Artificial Intelli-
gence, pages 99–108. Springer.
Fan, Z., Shen, H., Wu, Y., and Li, Y. (2013). Simulated-
annealing load balancing for resource allocation in
cloud environments. In 2013 International Confer-
ence on Parallel and Distributed Computing, Appli-
cations and Technologies, pages 1–6. IEEE.
Hassan, N., Yau, K.-L. A., and Wu, C. (2019). Edge com-
puting in 5g: A review. IEEE Access, 7:127276–
127289.
Hmimz, Y., Chanyour, T., El Ghmary, M., and
Cherkaoui Malki, M. O. (2019). Energy efficient
and devices priority aware computation offloading to
a mobile edge computing server. In 2019 5th Interna-
tional Conference on Optimization and Applications
(ICOA), pages 1–6. IEEE.
Huang, L., Feng, X., Zhang, L., Qian, L., and Wu, Y.
(2019). Multi-server multi-user multi-task computa-
tion offloading for mobile edge computing networks.
Sensors, 19(6):1446.
Li, H. (2018). Multi-task offloading and resource allocation
for energy-efficiency in mobile edge computing. Int.
J. Comput. Tech, 5:5–13.
Lyu, X., Tian, H., Sengul, C., and Zhang, P. (2016). Mul-
tiuser joint task offloading and resource optimization
in proximate clouds. IEEE Transactions on Vehicular
Technology, 66(4):3435–3447.
Rahati-Quchani, M., Abrishami, S., and Feizi, M. (2019).
An efficient mechanism for computation offload-
ing in mobile-edge computing. arXiv preprint
arXiv:1909.06849.
Sabella, D., Vaillant, A., Kuure, P., Rauschenbach, U., and
Giust, F. (2016). Mobile-edge computing architecture:
The role of mec in the internet of things. IEEE Con-
sumer Electronics MagazinEE, 5(4):84–91.
Xu, J., Hao, Z., and Sun, X. (2019). Optimal offloading de-
cision strategies and their influence analysis of mobile
edge computing. Sensors, 19(14):3231.
You, C., Huang, K., Chae, H., and Kim, B.-H. (2016).
Energy-efficient resource allocation for mobile-edge
computation offloading. IEEE Transactions on Wire-
less Communications, 16(3):1397–1411.
Zhang, K., Mao, Y., Leng, S., Zhao, Q., Li, L., Peng, X.,
Pan, L., Maharjan, S., and Zhang, Y. (2016). Energy-
efficient offloading for mobile edge computing in 5g
heterogeneous networks. IEEE access, 4:5896–5907.