Optimization of Cholera Spreading using Sanitation, Quarantine,
Education and Chlorination Control
Subchan Subchan
1
, Sentot D. Surjanto
1
, Irma Fitria
2
and Dwita S. Anggraini
1
1
Departement of mathematics, Institut Teknologi Sepuluh Nopember, Surabaya, Indonesia
2
Departement of mathematics, Institut Teknologi Kalimantan, Balikpapan, Indonesia
Keywords:
Cholera Model, Optimal Control, Pontryagin Minimum Principle.
Abstract:
Cholera is a contagious and deadly disease that requires an effective prevention and control actions. In this
paper, several efforts are made to prevent the cholera spreading by reconstructing the mathematical model and
adding control sanitation, treatment consisted of quarantine and education as well as chlorination on to the
bacteria. The Pontryagin Minimum Principle is employed to derive the optimal control solution and solved by
Runge-Kutta method. The computational results showed that the control was able to minimize the number of
individuals infected by cholera with mild symptoms at the final time as many as 2 individuals and individuals
infected by cholera with severe symptoms at the final time as many as 7 individuals as well as minimize the
number of bacteria concentrations at the final time as much as 517 cell/ml.
1 INTRODUCTION
Cholera is an acute diarrhea infection which is caused
by the consumption of food or water contaminated
with Vibrio cholerae bacteria (Organization, 2008).
These bacteria secrete enterotoxins in the intestinal
tract which cause diarrhea accompanied with acute
and severe vomiting. Therefore, an individual will
lose a lot of body fluids only in several days and get
dehydration. This condition can cause death if not
handled quickly (Johnson and R, 2006). The spread-
ing process of cholera can occur through the mouth,
when Vibrio Cholerae bacteria successfully entered
through the mouth and ingested, then these bacte-
ria will be quickly killed when exposed to stomach
acid. However, if Vibrio Cholerae bacteria success-
fully passes the stomach acid, the bacteria will de-
velop in the small intestine (Setiadi, 2014).
About 75% of people infected with Vibrio cholera
do not experience any symptoms, even though the
bacteria are in their feces for 7-14 days after infected
(Organization, 2008), but when there is an infec-
tion attack then the diarrhea and vomiting suddenly
occur with serious condition as acute attack (Sack
et al., 2004). Since 1917, cholera has been known
as seven pandemics which spread to Europe. The
Vibrio Cholerae bacteria first appeared in Sulawesi,
Indonesia and caused a cholera epidemic. Cholera
then spread rapidly to other East Asian countries and
reached Bangladesh in 1963, India in 1964 and the
Soviet Union, Iran and Iraq in 1965-1966 (Setiadi,
2014).
Cholera is rapidly spreading in densely populated
areas, poor water sanitation and lack of clean wa-
ter supply. Therefore, cholera is widely identified in
poor and developing countries (Subchan et al., 2019).
So that it does not rule out the possibility of cholera
spreading in Indonesia, for it is important to conduct
research on controlling the spread of cholera in order
to minimize cases of the spread of cholera.Effective
precautions of controlling for cholera depend on pro-
viding adequate environmental health services, such
as increasing access to clean water, sanitation, avail-
ability of cholera vaccines, quarantine and treatment
(Organization, 2008).
The mathematical model related to cholera
spreading with its control had been many conducted
in the previous research. The research about cholera
disease had been examined by Bakhtiar (Bakhtiar,
2015). He studied optimum control approach of con-
tagious disease with the control variable was the role
of education and chlorination. After that, Lemos-
Paiao et al (Lemos-Pai
˜
ao et al., 2016), concerned on
cholera spreading model by giving control in the form
of treatment done to the population of quarantined
people. The population infected which was given a
treatment would be quarantined so that it obtained the
quarantined population. In addition, Subchan et al
236
Subchan, ., Surjanto, S., Fitria, I. and Anggraini, D.
Optimization of Cholera Spreading using Sanitation, Quarantine, Education and Chlorination Control.
DOI: 10.5220/0009881902360240
In Proceedings of the 2nd International Conference on Applied Science, Engineering and Social Sciences (ICASESS 2019), pages 236-240
ISBN: 978-989-758-452-7
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

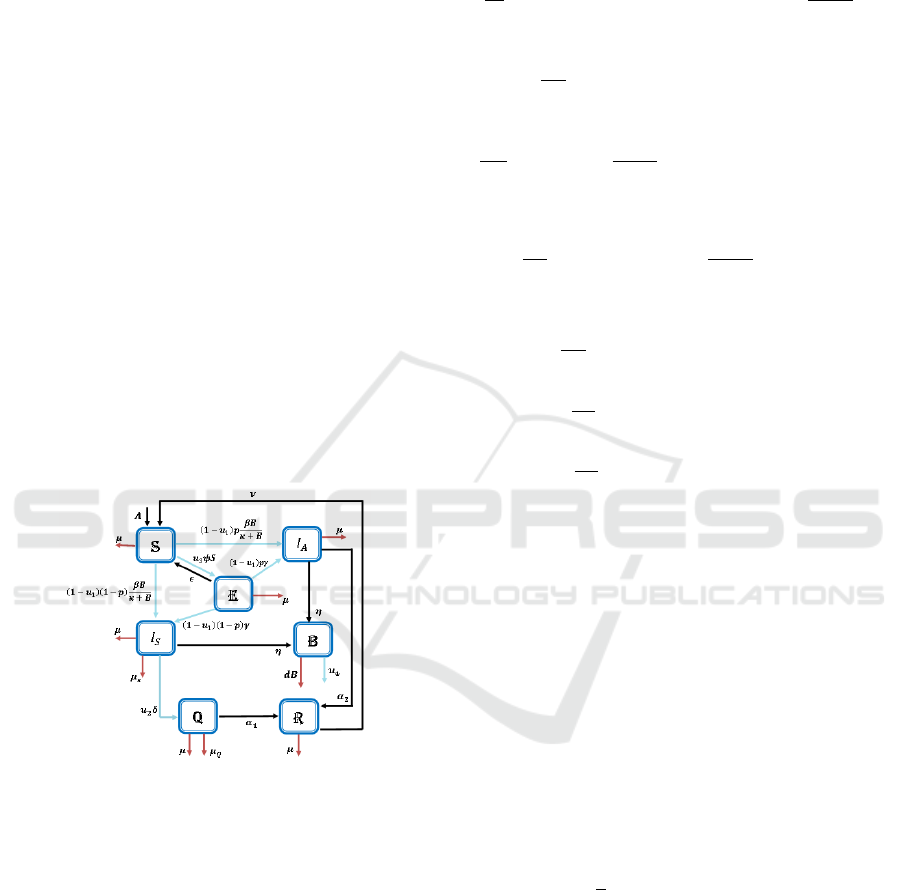
(Subchan et al., 2019). reasearched cholera disease
spreading model by giving the optimal control in the
forms of medication and intervention through the im-
provement of sanitation, education and quarantine.
In this research, the problem was reconstructed by
the mathematical model of the spread of cholera with
the control variable in the form of chlorination in bac-
teria, improved sanitation, education and quarantine.
Control was given to reduce the number of individuals
infected with cholera with mild and severe symptoms
and reduce proliferation of the Vibrio Cholerae bacte-
ria.
2 MATHEMATICAL MODEL
In this research, the type of mathematical model of
cholera spreading used was the type of SEIQR which
was reconstructed by adding chlorine to the bacteria
(u
4
). Other optimal controls were based on the re-
search (Subchan et al., 2019), which are improvement
of sanitation (u
1
), control treatment in the form of
medication during quarantine for infected individuals
(u
2
) and education for vulnerable individuals (u
3
).
Figure 1: SEIQR Compartment Diagram the Spread of
Cholera.
The spread of water-based diseases, especially
cholera, can be reduced by the use of chlorine which
is believed to be effective in reducing bacteria. In ad-
dition, sanitation improvements are carried out to re-
duce the level of absorption of bacteria caused by in-
fected individuals. Control treatment is also given to
people with cholera through quarantine to accelerate
healing of infected individuals and prevent spread to
vulnerable individuals. In addition, education is also
provided to individuals who are vulnerable to cholera
as an effort to prevent the outbreak of the disease.
The interpretation of the mathematical model of
cholera spreading by giving optimal control to the
compartment diagram as shown in the Fig. 1. The
mathematical models of the spread of cholera are as
follows.
ds
dt
= Λ +νR + εE −µS −u
a
ψ− (1− u
1
)
βB
κ + B
S (1)
dE
dt
= uaψS − εE − µE − (1 −u
1
)γE (2)
dI
A
dt
= (1 −u
1
)p
βB
κ + B
S + (1 − u
1
)pγE − µI
A
− α
2
I
A
(3)
dI
s
dt
= {(1 −u
1
)(1 − p)
βB
κ + B
S + (1 − u
1
)
(1 − p)γE − µI
s
− µ
s
I
s
= u
2
δI
s
}
(4)
dQ
dt
= u
2
δI
s
− µQ −µ
Q
Q − α
1
Q (5)
dR
dt
= α
1
Q + α
2
I
A
− µR −νR (6)
dB
dt
= ηI
A
+ ηI
S
− dB −U
4
B (7)
with the variables and parameters that formed up
the system can be seen in Figure 2. It is assumed
that S, E, I
A
, I
S
, Q, R ≥ 0 and all parameters are posi-
tive, which are taken from (Subchan et al., 2019)
3 OPTIMAL CONTROL
PROBLEMS
The purpose of this research is to obtain control by
minimizing the number of infected human popula-
tions, bacterial populations and minimizing the costs
incurred for controls by considering equations (1)-(7).
The objective function can be defined as follows
J(x, u) = {
1
2
Z
t
0
t
f
[C
1
I
2
S
(t)] +C
2
I
2
A
(t)
+C
3
B
2
(t) +C
4
u
2
1
(t) +C
5
u
2
2
(t)
+C
6
u
2
3
(t) +C
7
u
2
4
(t)d t}
(8)
with t
0
as initial time and t
f
is final time, and
C
i
was the parameter weight or price coefficient is-
sued at each control, where C
i
> 0 for each i =
1, 2, 3, 4, 5, 6, 7.
Optimization of Cholera Spreading using Sanitation, Quarantine, Education and Chlorination Control
237

The first step to solve the optimal control problem
using the Pontryagin Minimum Principle is to define
(Subchan and Zbikowski, 2007) as follows
H = {
1
2
(C
1
I
2
S
(t) +C
2
I
2
A
(t)
+C
3
B
2
(t) +C
4
u
2
1
(t) +C
5
u
2
2
(t)
+C
6
u
2
3
(t) +C
7
u
2
4
(t))+
λ
S
(Λ + νR + εE − µS − u
3
ψS − (1 − u
1
)
βB
(κ + B)
S) + λ
E
(u
3
ψS − εE−
µE − (1 − u
1
)γE) + λ
(
I
A
)((1 −u
1
)p
βB
(κ + B)
S + (1 − u
1
)pγE−
µI
A
− α
2
I
A
) + λ
(
I
S
)((1 − u
1
)(1 − p)
βB
(κ + B)
S + (1 − u
1
)(1 − p)γE
− µI
S
− µ
S
I
S
− u
2
δI
S
) + λ
Q
(u
2
δI
S
− µQ − µ
Q
Q − α
1
Q)
+ λ
R
(α
1
Q + α
2
I
A
− µR − νR)
+ λ
B
(ηI
A
+ ηI
S
− dB − u
4
B)}
(9)
where λ
i
for each i = S, E, I
A
, I
S
, Q, R, B was the
costate vector or Lagrange multiplier that depended
on the state. Next, the optimal control value u
∗
1
, u
∗
2
, u
∗
3
and u
∗
4
was found as follows
u
∗
1
= {
1
C
4
(
βB
κ + B
S(Pλ
I
A
+ λ
I
S
(1 − p) − λ
S
)
+ γE(λ
I
A
P + λ
I
S
(1 − p) − λ
E
)}
(10)
u
∗
2
=
δI
S
(λ
I
S
− λ
Q
)
C
5
(11)
u
∗
3
=
ΨS(λ
S
− λ
E
)
C
6
(12)
u
∗
4
=
λ
B
B
C
7
(13)
The optimal control u
∗
was obtained from
∂H
∂u
and
had the following characteristics
u
∗
1
= min(u
1min
, max(
ˆ
u
∗
1
, u
1max
))
u
∗
2
= min(u
2min
, max(
ˆ
u
∗
2
, u
2max
))
u
∗
3
= min(u
1min
, max(
ˆ
u
∗
3
, u
1max
))
u
∗
4
= min(u
1min
, max(
ˆ
u
∗
4
, u
1max
))
Figure 2: Variables and Parameters on Mathematical Mod-
els of the Spread of Cholera.
Equations (10)-(13) were substituted to Equation
(9) so that it had the optimal Hamiltonian function
H
∗
. The next step was to determine the state equation
(Subchan and Zbikowski, 2007) as follows
˙
S
∗
= {Λ + νR + εE − µS − u
∗
3
ΨS − (1 − u
∗
1
)
βB
(κ + B)
S}
(14)
˙
E
∗
= u
∗
3
ΨS − εE − µE − (1 − u
∗
1
)γE
(15)
˙
I
∗
A
= p
βB
(κ + B)
S + (1 − u
∗
1
)pγE − µI
A
− α
2
I
A
(16)
˙
I
∗
S
= {(1 − u
∗
1
)(1 − p)
βB
(κ + B)
S + (1 − u
∗
1
)
(1 − p)γE − µI
S
− µ
S
I
S
− u
∗
2
δI
S
}
(17)
˙
Q
∗
= u
∗
2
δI
S
− µQ − µ
Q
Q − α
1
Q
(18)
˙
R
∗
= α
1
Q + α
2
I
A
− µR − νR
(19)
˙
B
∗
= ηI
A
+ ηI
S
− dB − u
∗
4
B
(20)
And costate equations can be derived as follows
λ
∗
S
= − (−µλ
S
− u
∗
3
ψλ
S
− (1 − u
∗
1
)
βB
κ + B
λ
S
+ u
∗
3
ψλ
E
+ (1 − u
∗
1
)p
βB
κ + B
λ
I
A
+ (1 − u
∗
1
)(1 − p)
βB
κ + B
λ
I
S
)
(21)
λ
∗
E
= − (ελ
S
− ελ
E
− µλ
E
− (1 − u
∗
1
)
γλ
E
+ (1 − u
∗
1
)pγλ
I
A
+ (1 − u
∗
1
)
(1 − p)γλ
I
S
)
(22)
λ
∗
I
A
= − (C
2
I
A
− µλ
I
A
− α
2
λ
I
A
+ α
2
λ
R
+ ηλ
B
)
(23)
ICASESS 2019 - International Conference on Applied Science, Engineering and Social Science
238

λ
∗
I
S
= − (C
1
I
S
− µλ
I
S
− µ
S
λ
I
S
− u
∗
2
δλ
I
S
+ u
∗
2
δλ
Q
+ ηλ
B
)
(24)
λ
∗
Q
= − (−µλ
Q
− µ
Q
λ
Q
− α
1
λ
Q
+ α
1
λ
R
)
(25)
λ
∗
R
= − (νλ
S
− µλ
R
− νλ
R
)
(26)
λ
∗
R
= − (C
3
B + λ
S
(1 − u
∗
1
)
βS
κ
(κ + B)
2
+ λ
I
A
(1 − u
∗
1
)
pβS
κ
(κ + B)
2
+ λ
I
S
(1 − u
∗
1
)
(27)
The optimal state and costate then can be deter-
mined by considering the boundary condition x(0)
= x
0
and λ(t
f
) = 0.
4 COMPUTATIONAL RESULT
The parameter values are taken from (Subchan et al.,
2019) and used for numerical simulation. The simu-
lation is solved by using Fordward-Backward Sweep
Runge-Kutta Order 4 method (Lenhart and Work-
man, 2007; Burden et al., 2016; Lindfield and Penny,
1995). The purpose of numerical simulation was to
determine the effectiveness of optimal control in each
population. The simulation result on every population
can be seen on Fig. 3 and the control can be seen on
Fig. 4.
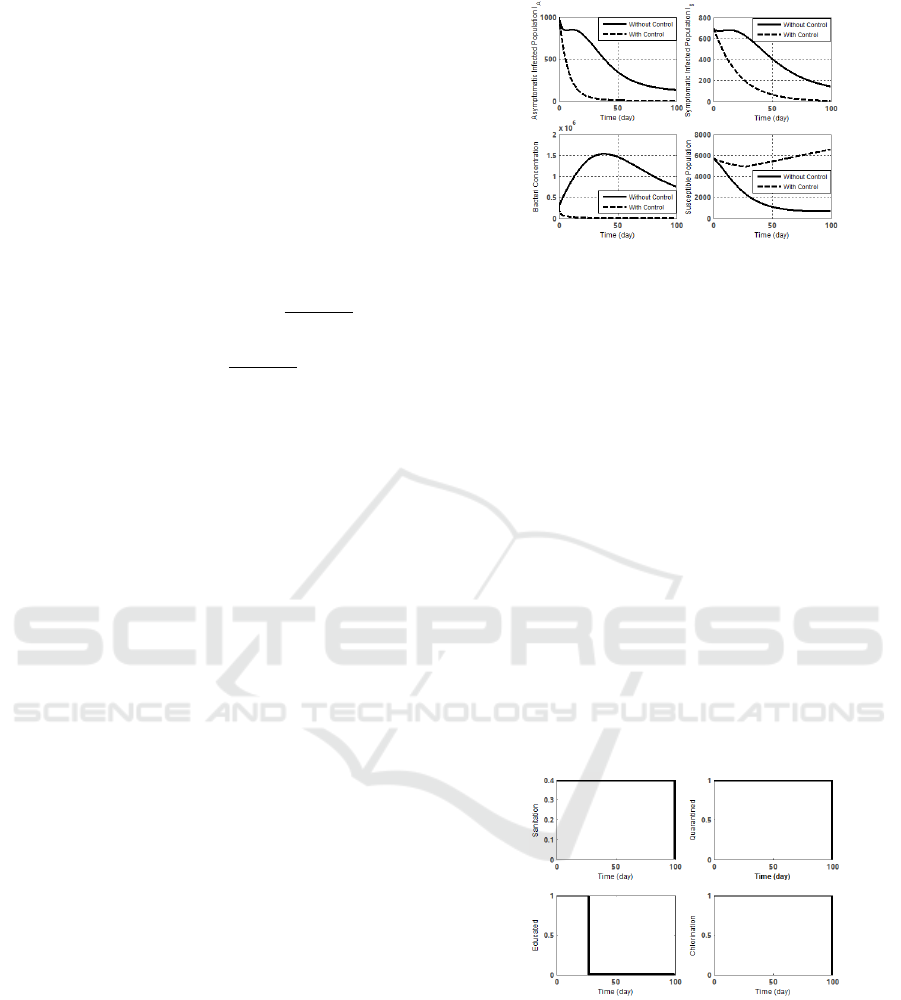
Based on Fig. 2, it was known that infected
asymptomatic individual decreased. The number of
infected asymptomatic individuals with the final time
without optimal control was 133 individuals while
with control the number of individuals at the end of
time was 2 individuals. This was due to the large in-
fluence of β parameter, which was the level of con-
sumption of bacteria through contaminated sources.
If the value of β was getting bigger, then the number
of individuals without optimal control would be even
less. It caused the individuals with mild symptoms to
change into severe symptoms if individuals were not
aware of the symptoms because of lacking the knowl-
edge or neglected the individual education. So, in this
case the effectiveness of giving control in the infected
asymptomatic subpopulation had an effect of 98.50%.
So, the objective to minimize the number of individu-
als with mild symptoms had been reached.
Figure 3: The Change of Rate on the Number of Infected
Asymptomatic (I
A
) population, Infected Symptomatic (I
S
),
Bacteria and Susceptible concentration.
Furthermore, the infected symptomatic individual
also decreased when control is given. The number of
infected symptomatic individuals with the final time
without control was 145 individuals while with con-
trol, the number of individuals at the end was 7 in-
dividuals. The number of infected symptomatic indi-
viduals without control increased 680 individuals at
t = 15, while with control, the number of infected
symptomatic individuals were decreased at the begin-
ning until the end. It means that the level of control
effectiveness had an effect of 95.17%. The concentra-
tion of bacteria decreased with control. The amount
of bacterial concentration at the end without control
was 7, 5 ∗ 10
5
while with control the number of bac-
terial concentrations at the end was 517. In this case,
control had an effect of 99.93%. Based on Fig. 3,
it was shown that the level of control of individuals
and bacteria was on maximum value 1 and sanitation
control was at value 0.4.
Figure 4: Sanitation (u
∗
1
), Quarantine (u
∗
2
), Education (u
∗
3
)
and Chlorination (u
∗
4
).
Based on Fig. 5, it can be seen that the level of
susceptible population decreased since the beginning.
This was caused by the number of susceptible popu-
lation interacted with cholera bacterial-contaminated
environment so the population were infected. Further-
more, the population increased at about t = 27. The
educated population was increased from the very first
time and it was proportional to susceptible population
level. The quarantine population increased sharply at
Optimization of Cholera Spreading using Sanitation, Quarantine, Education and Chlorination Control
239

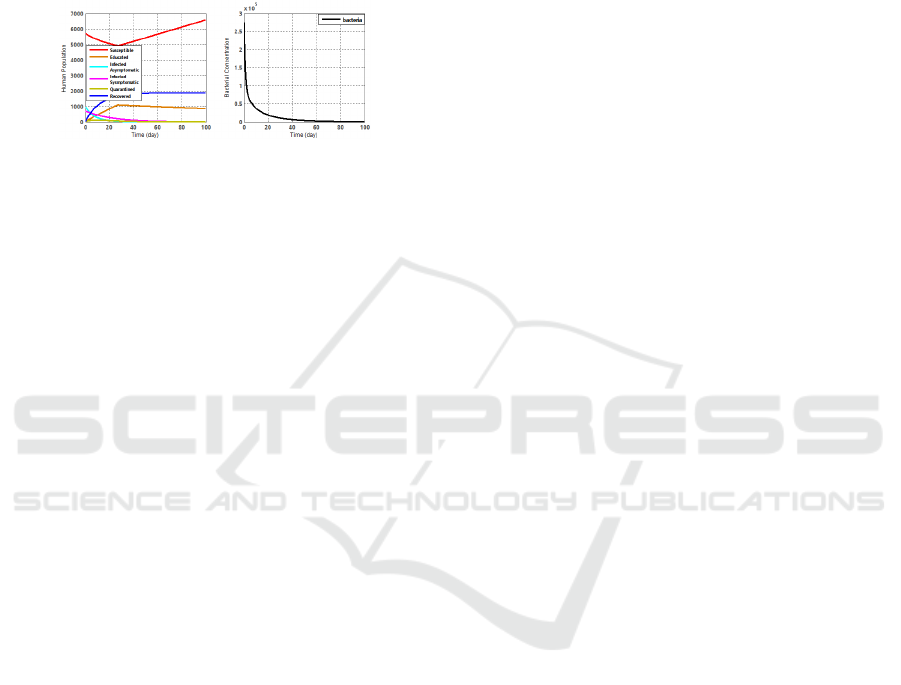
the beginning till day 15, then it decreased until the
end. This is caused by infected symptomatic popula-
tion decreased.
In this case, the recovered population increased
from the beginning then it stay in the certain value
until the end. The asymptomatic and symptomatic in-
fected population decreased because bacteria concen-
tration level kept decrease until the end.
Figure 5: The Change of Subpopulation Rate and Bacteria
Concentration with Control.
5 CONCLUSION
In this paper, system of differential equations were
given as the dynamics model of cholera spreading
that was divided into human population and bacteria
population classes. The optimal control in the form
of sanitation, chlorination, education, and quarantine
were given as the attempt to control cholera spread-
ing.
The simulation result showed the effect of the
given control. Based on the computational result,
controls affected the number of infected population
and bacteria experienced decline so that cholera en-
demic was not quite big problem. This showed that
the optimum control strategy in the form of sanitation,
chlorination, education, and quarantine gave signifi-
cant positive effect to minimize the spread of cholera.
ACKNOWLEDGEMENTS
The authors wish to thank Department of Mathemat-
ics, Institut Teknologi Sepuluh Nopember and Institut
Teknologi Kalimantan for their support and funding.
REFERENCES
Bakhtiar, T. (2015). Peran edukasi dan klorinasi dalam pen-
gendalian penyakit menular: Sebuah pendekatan kon-
trol optimum. Semirata, 1.
Burden, R., Faires, J., and Burden, A. (2016). Numerical
Analysis. Cengage Learning, Boston USA.
Johnson and R, L. (2006). Mathematical modeling of
Cholera: from bacterial life histories to human epi-
demics. s.l.:University of California, Santa Cruz.
Lemos-Pai
˜
ao, S., a., A., Torres, C., and FM, D. (2016). An
epidemic model for cholera with optimal control treat-
ment. Journal of Computational and Applied Mathe-
matics.
Lenhart, S. and Workman, J. T. (2007). Optimal control
applied to biological models. CRC Press, Taylor and
Francis Group, London.
Lindfield, G. and Penny, J. (1995). Numerical Method Us-
ing MATLAB. MPG Book Ltd, Botmin Cornwall.
Organization, W. H. (2008). Prevention and control of
cholera outbreaks: WHO policy and recommenda-
tions. s.n, s.l.
Sack, David, A., Sack, R., Nair, G., and Siddique, A.
(2004). Cholera. Lancet, 363:223–33.
Setiadi, S. (2014). Ilmu Penyakit Dalam. Interna Publish-
ing, Jakarta.
Subchan, S., A.M., a. I., and F. (2019). An epidemic cholera
model with control treatment and intervention. IOP
Publishing, s.l.
Subchan, S. and Zbikowski, R. (2007). Computational op-
timal control of the terminal bunt manoeuvre—part 1:
Minimum altitude case. Optimal Control Applications
and Methods, 28(5):311–325.
ICASESS 2019 - International Conference on Applied Science, Engineering and Social Science
240