On Bayes Factors for Success Rate A/B Testing
Maciej Skorski
DELL, Austria
Keywords: Hypothesis Testing, Bayesian Statistics, AB Testing, Information Geometry.
Abstract:
This paper discusses Bayes factors, an alternative to classical frequentionist hypothesis testing, within the
standard A/B proportion testing setup - observing outcomes of independent trails (which finds applications
in industrial conversion testing). It is shown that the Bayes factor is controlled by the Jensen-Shannon di-
vergence of success ratios in two tested groups, and the latter one is bounded (under mild conditions) by
Welch’s t-statistic. The result implies an optimal bound on the necessary sample size for Bayesian testing, and
demonstrates the relation to its frequentionist counterpart (effectively bridging Bayes factors and p-values).
1 INTRODUCTION
1.1 Background and Motivation
A/B Proportions Testing. A/B testing is the
methodology of collecting data from two parallel ex-
periments, and deciding which group performs better
by means of statistical inference (to account for ef-
fects that may be due to change). The most frequent
use case concerns two success-counting experiments,
for example how many customers convert (purchase,
subscribe etc) on two versions of a web page (for ex-
ample the old page vs the optimized one).
In order to make the decision statistic-driven the
business question is formulated as the question about
unknown conversion rates p
1
, p
2
in the compared
groups, that are to be estimated from collected (ob-
served) data D . Usually one states the problem as
choosing one of the two possibilities
(a) The null hypothesis states that conversion rates
are equal (zero-effect), written as H
0
= {p
1
= p
2
}
(b) The alternative hypothesis claims a difference,
for example H
a
= {p
1
6= p
2
} or H
a
= {p
1
=
p
2
+ δ}
A/B Model Assumptions. We assume that in each
of the two groups we observe r independent Bernoulli
variables (each one is success or failure). Success
rates p
i
for group i are to be estimated from ths data
(we allow unknown rates p
i
to depend on hypothe-
ses via prior distributions). The data set D contains
two binary sequences describing outcomes (success
or failure for each trial) for each of the two groups.
Statistical Testing and Bayes Factors. The fre-
quentionist approach falsifies the null hypothesis
based on the two-sample t-test (Welch, 1938), so that
it is rejected when the test value is sufficiently un-
likely for given data (probability of which, falsely re-
jecting the null, is p-value).
The Bayesian approach is more coherent and flex-
ible as it directly compares the likelihoods of two hy-
potheses (for given data). By Bayes’ theorem
Pr[H
0
|D]
Pr[H
a
|D]
| {z }
posterior odds
=
Pr[D|H
0
]
Pr[D|H
a
]
| {z }
data likelihood ratio
·
Pr[H
0
]
Pr[H
a
]
| {z }
prior odds
(1)
where the likelihood ratio
K =
Pr[D|H
0
]
Pr[D|H
a
]
(2)
is also called the Bayes factor. Prior odds usually
equal 1, when one gives no prior preference to H
0
or
H
a
. Then the posterior odds equal K and the decision
depends on its magnitude: the bigger K from 1, the
more it supports H
0
. This may be also seen as decid-
ing upon the expected (posterior) cost of a certain risk
function (Lavine and Schervish, 1999).
Confidence scales depending on the magnitude
have been developed (Kass and Raftery, 1995; Jef-
freys, 1998; Lee and Wagenmakers, 2014).
Hypotheses are arbitrary “prior” probabilities on
rates p
1
, p
2
which can be formally written as H =
{(p
1
, p
2
) → P
H
(p
1
, p
2
)}. This includes point state-
ments of the form H = {p
1
= p
2
= 0.01} as well
us uncertainty distributions such as beta priors H =
{p
1
= p
2
= p, p ∼ Beta(0.5,0.5)}. Priors usually are
weakly informative, that is they give less preference
to “unrealistic” values like those near 0 or 1.
332
Skorski, M.
On Bayes Factors for Success Rate A/B Testing.
DOI: 10.5220/0007954503320339
In Proceedings of the 8th International Conference on Data Science, Technology and Applications (DATA 2019), pages 332-339
ISBN: 978-989-758-377-3
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Under prior distributions specified the data likeli-
hood equals
Pr[D|H] =
Z
Pr[D|p
1
, p
2
] ·dP
H
(p
1
, p
2
)
=
Z
2
∏
i=1
p
¯p
i
r
i
(1 −p
i
)
(1− ¯p)
i
r
·dP
H
(p
1
, p
2
)
(3)
where r is the number of events and ¯p
i
is the success
rate observed for each group i in the collected data
D. Computation of the corresponding factor K can
be done in statistical software such as in R package
BayesFactor (Morey and Rouder, 2018).
1.2 Problem: Bayesian A/B testing
Estimates, neither frequentionist nor bayesian, will
not be conclusive without sufficiently many samples.
Frequentionists widely use rules of thumbs that are
derived based on t-tests. Under the bayesian method-
ology this is little more complicated because hypothe-
ses can be arbitrary priors over parameters (hence
composed out of infinitely many choices). Under the
described A/B model, we answer the following ques-
tions
• When, given data, a bayesian hypothesis on zero
effect may be rejected (we want to guarantee that
for any H
0
it holds K  1 for some H
a
)?
• What is the relation to the classical t-test?
• What are most plausible null and alternative hy-
pothesis, for a given dataset?
This will allow us to understand data limitations when
doing bayesian inference, and relate them to widely-
spread frequentionists rules of thumb. It is impor-
tant to note that Bayesian modelling has recently be-
come very popular in industrial conversion optimiza-
tion (Keser, 2017), so that these questions are also of
considarable practical interest.
1.3 Related Works and Contribution
Our problem, as stated, is a question about maximiz-
ing minimal Bayes factor; this is because we compare
any null against its most favorable alternative. For
certain simple problems, particularly for testing nor-
mality, minimal Bayes factors are known to be related
to frequentionists p-values (Edwards et al., 1963;
Kass and Raftery, 1995; Goodman, 1999), which
bridges the Bayesian and frequentionists worlds. This
should be contrasted with a wide-spread belief that
both methods are very incompatible (Kruschke and
Liddell, 2018).
The novel contributions of this paper are (a) de-
termining the Bayes factor - for testing success ratios
(b) demonstrating the relation to the frequentionist ap-
proach and (c) discussion of Bayesian sample bounds.
To the best author’s knowledge, this is the first result
of this sort in the context of testing success rates in
independent trials.
1.3.1 Main Result: Bayes Factor and Welch’s
Statistic
The following theorem shows that no “zero-effect”
hypothesis can be falsified, unless the number of sam-
ples is big in relation to a certain data statistic. This
statistic turns out to be the Jensen-Shannon diver-
gence, well-known in information theory; we further
show how to relate it to the Welch’s t-statistic. Doing
so we connect the classical frequentionist analysis and
the Bayes factors analysis.
Theorem 1 (Bayes Factors for Success Rate Testing).
Consider two experiments, each with r independent
trials with unknown success probabilities p
1
and p
2
respectively. If observed data D has r · ¯p
i
successes
for group i = 1,2, then
max
H
0
:{p
1
=p
2
}
min
H
a
Pr[D|H
0
]
Pr[D|H
a
]
= e
−2r·JS( ¯p
1
, ¯p
2
)
(4)
where the maximum is over null hypotheses H
0
such
that p
1
= p
2
, the minimum is over all valid alternative
hypotheses (priors) H
a
over p
1
, p
2
, and JS denotes
the Jensen-Shannon divergence.
When comparing the Jensen-Shannon divergence
with the Welch’s t-statistic one should note that the
second one is unbounded, as illustrated in Figure 1.
Specifically, the Welch’s t is unbounded where one
rate is close to zero but the second one is closed to
one. It is however possible to have a bound of the
form JS = Ω(t
2
Welch
), under mild additional assump-
tions for example when both rates are smaller than 0.5
(which in practice don’t limit the usability). The re-
sult is formally stated in the theorem below, the proof
appears in Section 4. We note that the current proof
fails to achieve the optimal constant (see Section 5).
Theorem 2 (Comparison with T-Test). Under the
condition 0 6 ¯p
1
, ¯p
2
6
1
2
it holds that the Jensen-
Shannnon divergence is bounded from below by the
Welch’s t-statistic
JS( ¯p
1
, ¯p
2
) >
t
Welch
(r, ¯p
1
, ¯p
2
)
2
32r
(5)
so that the Bayes factor in Equation (4) can be
bounded by
max
H
0
:{p
1
=p
2
}
min
H
a
Pr[H
0
|D]
Pr[H
a
|D]
6 e
−t
Welch
(r, ¯p
1
, ¯p)
2
/16
. (6)
On Bayes Factors for Success Rate A/B Testing
333

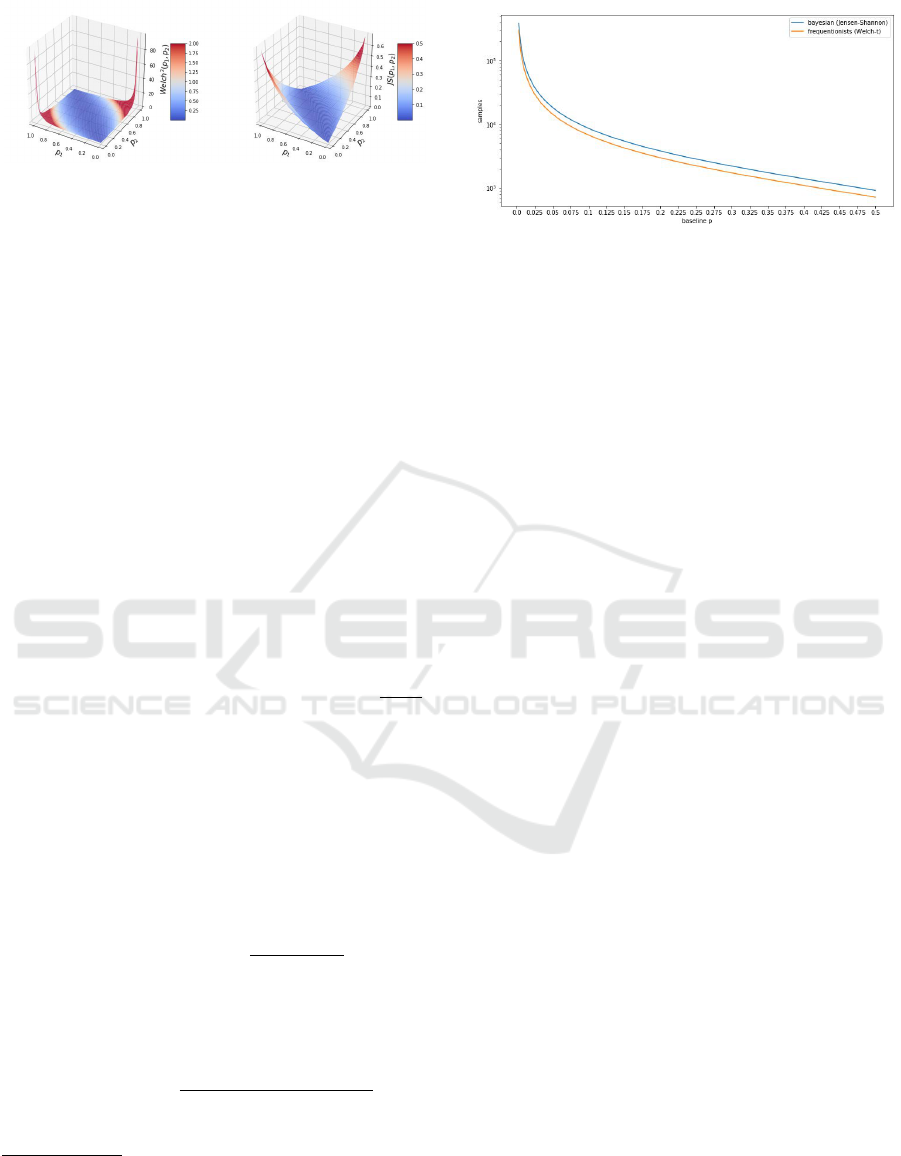
Figure 1: Surface plots of the squared t-statistic t
2
Welch
(left) and Jensen-Shannon divergence JS which controls the
Bayes factor (right), as functions of success rates p
1
, p
2
.
Note that t
Welch
is unbounded (around the corners).
Remark 1 (Min-max Game Intepretation). The min-
max formula in Equation (6) comes from the fact that
we evaluate every null against its most plausible al-
ternative (so that the bound holds regardless of the
null prior). This can be seen as a two-player zeros-
sum game where one player chooses the null hypothe-
sis, the second player chooses the alternative and the
payoff is the Bayes factor. Theorem 1 describes the
saddle point in this game.
The following corollary shows what are most
“plausible” null and alternatives for a given data set
(they realize equality in Equation (4))
Corollary 1 (Characterization of Most Favorable Hy-
potheses). Note that
• Maximally favorable alternative (H
a
which maxi-
mizes Pr[D|H
a
]) is p
1
= ¯p
1
and p
2
= ¯p
2
• Maximally favorable null H
0
on zero-effect, that is
of the form p
1
= p
2
, is given by p
1
= p
2
=
¯p
1
+ ¯p
2
2
If null is of the form p
1
= p
2
= p for some constant p,
then the bound becomes e
−r·KL( ¯p
1
,p)−r·KL( ¯p
2
,p)
.
1.3.2 Application: Sample Bounds
The main result implies the following sample size rule
Corollary 2 (Bayesian Sample Bound). To confirm
the non-zero effect (p
1
6= p
2
) the number of samples r
for the bayesian method should be
r
bayes
> log K
critical
·
1
2JS( ¯p
1
, ¯p
2
)
(7)
where usually K
critical
≈10
1
. Under the frequenionist
method the rule of thumb is t
Welch
 t
critical
, which
gives (see Section 2)
r
f req
> t
critical
·
¯p
1
(1 − ¯p
1
) + ¯p
2
(1 − ¯p
2
)
( ¯p
1
− ¯p
2
)
2
(8)
where usually t
critical
≈ 1.9
2
1
This corresponds to the Bayes factor of 10
−1
against
null, interpreted as strong evidence in common scales (Lee
and Wagenmakers, 2014).
2
This roughly holds for the significance level of 0.95,
the exact value depends also on degrees of freedom.
Figure 2: Comparison of the bayesian (7) and the frequen-
tionist (8) sample lower bounds, where observed data are
¯p
1
= p and ¯p
2
= p ·(1 + δ) for δ = 0.1 (relative uplift by
10%), and the zero-effect hypothesis p
1
= p
2
is to be re-
jected. Bounds are away by a constant factor, here are very
close for constants calibrated under typical rejection rules:
t-statistic of 1.9 and Bayes factor of 0.1.
Note that both formulas needs assumptions on lo-
cations of expected rates; testing smaller effects or
smaller conversion rates require more samples.
Exact constants, hidden under K
critcal
and t
critcal
,
depend on the significance one wants to achieve: p-
value for the extreme t-statistic, respectively the mag-
nitude of the Bayes factor. Apart from constants
(or when constants are callibrated for “typical” tests
strength) bounds in Equation (7) and Equation (8) are
close to each other. The difference is illustrated on
Figure 2, for the case when one wants to prove the
difference (reject the zero-effect hypothesis) in pres-
ence of an observed lift of 10%. The code is attached
in Section 5.
It is important to stress that our lower bounds hold
with respect to zero-effect hypotheses and regardless
of priors, testing effect of a fixed size or using more
diffuse priors may require more samples.
1.3.3 Application: Bayes Factors vs P-Values
Since high values of t
Welch
mean small p-values, we
conclude that the frequentionist p-values bound the
Bayes factor and indeed are evidence against a null-
hypothesis in the well-defined bayesian sense.
However, because of the scaling t
Welch
→
e
−Ω(t
2
Welch
)
in the minimal Bayes factor in Equa-
tion (6), Bayesian rejection corresponds to p-values
much lower than the standard frequentionist thresh-
old of 0.05. In a way, the bayesian approach is more
conservative and reluctant to reject than frequention-
ist tests; this conclusion is shared with (Goodman,
1999).
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
334

2 PRELIMINARIES
Entropy, Divergence. The binary cross-entropy of
p and q is defined by
H(p,q) = −plog q −(1 −p) log(1 −q) (9)
which becomes the standard (Shannon) binary en-
tropy when p = q, denoted as H(p) = H(p, p). The
Kullback-Leibler divergence is defined as
KL(p,q) = H(p,q) −H(p) (10)
and is non-negative. The Jensen-Shannon diver-
gence (Lin, 1991) is defined as
JS(p,q) =
1
2
KL

p,
p + q
2

+
1
2
KL

q,
p + q
2

(11)
being symmetric and non-negative (because KL di-
vergence is non-negative). Alternatively, using Equa-
tion (10) and Equation (9) we can write
JS(p,q) = H

p + q
2

−
1
2
H(p) −
1
2
H(q) (12)
which shows that the Jensen-Shannon divergence is
bounded.
The following lemma shows that the cross-entropy
function is convex in the second argument. This
should be contrasted with the fact that the entropy
function (of one argument) is concave.
Lemma 1 (Convexity of Cross-entropy). For any p
the mapping x →H(p, x) is convex in x.
Proof. Since −plog(·) for fixed p ∈ [0,1] is convex
we obtain
−γ
1
plog x
1
−γ
2
plog x
2
> −p log(γ
1
x
1
+ γ
2
x
2
)
for any x
1
,x
2
and any γ
1
,γ
2
> 0, γ
1
+ γ
2
= 1. Replac-
ing x
i
by 1 −x
i
and p by 1 −p in the above inequality
gives us also
−γ
1
(1 −p) log(1 −x
1
) −γ
2
(1 −p) log(1 −x
2
)
> −(1 − p)log(γ
1
(1 −x
1
) + γ
2
(1 −x
2
))
= −(1 − p)log(1 −γ
1
x
1
) −γ
2
x
2
)
Adding side by side yields
γ
1
H(p,x
1
) + γ
2
H(p,x
2
) > γ
1
H(p,x
1
) + γ
2
H(p,x
2
)
which finishes the proof. This argument works for
multivariate case, when p,x are probability vectors.
Convexity Properties of Jensen-Shannon Diver-
gence.
Lemma 2. Let δ = p −q, then for every fixed q we
have
∂
2
∂δ
2
JS(p,q) =
1
2

p
2
−2pq −q
2
+ 2q

p(p −1)(p + q)(p + q −2)
(13)
which is strictly positive for 0 < p, q < 1.
Proof. The derivative is calculated in Section 5, with
the Python package SymPy (Meurer et al., 2017). The
numerator (skiping the constant
1
2
) can be written as
2q(1 −q) + (p −q)
2
which is non-negative. The de-
numerator is non-negative because p,q are between 0
and 1.
Bernoulii Variables. For a Bernoulli variable with
success probability p we denote by Var(p) = p(1 −
p) the variance. We have the following identity
Var(p) + Var(q) = 2Var

p + q
2

−
(p −q)
2
2
(14)
which in particular demonstrates that the variance is
concave.
2-Sample Test. To decide whether means in two
groups are equal, under the assumption of unequal
variances, one performs the Welch’s t-test with the
statistic given by (Derrick et al., 2016)
t
Welch
=
µ
1
−µ
2
r
s
2
1
r
1
+
s
2
2
r
2
(15)
where s
i
are sample variances and µ
i
are sample
means for group i = 1,2. The null hypothesis is re-
jected unless the statistic is sufficiently high (in abso-
lute terms). In our case the formula simplifies to
Claim 1. If rθ
1
and rθ
2
success out of r trials have
been observed, respectively in the first and the second
group, then
t
Welch
(r,θ
1
,θ
2
) = r
1
2
·
θ
1
−θ
2
p
θ
1
(1 −θ
1
) + θ
2
(1 −θ
2
)
(16)
3 PROOF OF THEOREM 1
Notation. We change the notation slightly, un-
known success rates will be p and q, and the number
of observed successes r ·θ
1
,r ·θ
2
.
On Bayes Factors for Success Rate A/B Testing
335

Best Alternative. Maximizing over alll possible
priors P
a
over pairs (p,q) and using Equation (3) we
get
max
P
a
Pr[D|H
a
] =
max
P
a
Z
e
−rH(θ
1
,p)−rH(θ
1
,q)
P
a
(p,q)d(p,q) (17)
Since H(θ
1
, p) = H(θ
1
, p) + KL(θ
1
, p), H(θ
1
,q) =
H(θ
1
,q)+KL(θ
1
,q) and KL is non-negative we con-
clude that the maximum over the integrals equals
max
P
a
Pr[D|H
a
] = e
−rH(θ
1
)−rH(θ
2
)
(18)
achieved for P
a
being a unit mass at (p,q) = (θ
1
,θ
2
),
that is at observed rates.
Best Null. Let H
0
states that the effect is 0. This is
equivalent to a prior P
0
(p) on the baseline conversion
p with the condition q = p. We obain
Pr[D|H
0
] =
Z
e
−rH(θ
1
,p)−rH(θ
2
,p)
dP
0
(p) (19)
The integrand, due to Lemma 1, has a global maxi-
mum at some p. Thus the integral is maximized for
dP
0
(p) being a point mass.
Bayes Factor. Using the above observations on
most plausible hypotheses we can write the max-min
Bayes factor (in favor of H
0
) as
max
H
0
min
H
a
Pr[D|H
0
]
Pr[D|H
a
]
=
max
H
0
Pr[D|H
0
]
max
H
a
Pr[D|H
a
]
= e
−r·(H(θ
1
,p)+H(θ
1
,p)−H(θ
1
)−H(θ
2
))
(20)
Using the relation between the KL divergence and
cross-entropy we obtain
max
H
0
min
H
a
Pr[D|H
0
]
Pr[D|H
a
]
= e
−rKL(θ
1
,p)−rKL(θ
2
,p)
(21)
We will use the following observation
Claim 2. The expression KL(θ
1
, p) + KL(θ
2
, p) is
minimized under p = θ
∗
=
θ
1
+θ
2
2
, and achieves value
2JS(θ
1
,θ
2
).
Proof. We have
KL(θ
1
, p) + KL(θ
2
, p)
= H(θ
1
, p) + H(θ
2
, p) −H(θ
1
) −H(θ
2
)
Now the existence of the minimum at p = θ
∗
follows by convexity of p → H(θ
1
, p) + H(θ
2
, p),
proved in Lemma 1. We note that H(θ
1
, p) +
H(θ
2
, p) = 2H

θ
1
+θ
2
2
, p

for any p (by definition),
and thus for p =
θ
1
+θ
2
2
= θ
∗
we obtain H(θ
1
, p) +
H(θ
2
, p) = 2H(θ
∗
) and KL(θ
1
, p) + KL(θ
2
, p) =
2H(θ
∗
) −H(θ
1
) −H(θ
2
). This combined with the
definition of the Jensen-Shannon divergence finishes
the proof.
We can now bound Equation (21) as
min
H
a
Pr[D|H
0
]
Pr[D|H
a
]
6 e
−2r·JS(θ
1
,θ
2
)
(22)
This ends the proof of Theorem 1, from the proof we
also conclude Corollary 1.
4 PROOF OF THEOREM 2
In order to compare JS and t
Welch
we use the
parametrization q = p + δ. For convenience we
slightly abuse the notation writing t
Welch
(p,q) =
t
Welch
(r, p,q)/
√
r = t
Welch
(1, p, q). The result reduces
to the following lemma
Lemma 3 (Convexity of the Gap between
Jensen-Shannon Divergence and Welch’s t). In
the region
0 6 q 6 p 6
1
2
(23)
we have that JS(p,q) −
1
32
·t
Welch
(p,q)
2
is convex in
δ = p −q for any fixed q. In particular for every q it
achieves the minimal value at δ = 0, which is equal to
0.
Proof. It suffices to consider q 6 p as both JS and
t
Welch
are symmetric. Because of continuity we con-
sider the strict inequalities 0 < q < p <
1
2
. The proof
involves symbolic differentiation and factoring which
we do in the Python package SymPy (Meurer et al.,
2017).
We start with the ratio of the second derivatives
Claim 3 (Second Derivatives Ratio). We have that
∂
2
∂δ
2
JS(p,q)
∂
2
∂δ
2
t
Welch
(p,q)
=
1
4
·ψ ·φ (24)
where
ψ(p,q) =

p − p
2
+ q −q
2

3
p(1 − p)(p + q)(2 − p −q)
φ(p,q) =
p
2
−2pq −q
2
+ 2q
−2p
3
q + p
3
+ 3p
2
q + 6pq
3
−9pq
2
−3q
3
+ 4q
2
Proof of Claim. The code deriving formulas is in-
cluded in Section 5.
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
336

Claim 4 (Denumerator of φ is non-negative). Let V =
−2p
3
q + p
3
+3p
2
q +6pq
3
−9pq
2
−3q
3
+4q
2
be the
denumerator of φ. Then V > 4p
2
(1 −p
2
).
Proof of Claim. It holds that
∂
2
V
∂p
2
= 6·(p+q−2pq) =
6(p(1 −q) + q(1 − p)) which shows that V is con-
vex in p for all (p,q) ∈ [0, 1]
2
. Next, we have
∂V
∂p
=
−3(p −q)

2pq − p + 2q
2
−3q

. Looking for global
minimas we note that the second factor 2pq − p +
2q
2
−3q = −q(1 − p) − p(1 −q) −2q(1 −q) is al-
ways non-positive and zero if and only if p = q = 0
or p = q = 1. The first factor gives us q = p. Sum-
ming up, the global minimum for each p is given by
q = p. Substituting this we obtain V (p,q) > V (q,q) =
4p
2
(1 −p)
2
which finishes the proof.
Claim 5 (Bound on φ). Let U,V be as before. Un-
der the condition 0 < q < p <
1
2
we have U · p(1 −
p) −
1
2
V > 0, and the claim before implies φ =
U
V
>
1
2p(1−p)
.
Proof of Claim. We have
U p(1 −p) −
V
2
=
p −q
2

1
2
−p

1
2
p
2
−pq −
3
2
q
2
+ 2q

=
p −q
2

1
2
−p

(p −q)
2
2
+ 2q(1 −q)

which is non-negative when
1
2
> p > q > 0. By the
previous claim U is non-negative so that we can di-
vide both sides. For completeness we include the
code used for deriving the formulas in Section 5.
Summing up, from the claims we obtain
Claim 6 (Bounding the Second Derivative Ratio).
Under the condition 0 < q < p <
1
2
we have
∂
2
∂δ
2
JS(p,q)
t
Welch
(p,q)
>
(Var(p) + Var(q))
3
32Var
2
(p)Var

p+q
2

(25)
which is bigger than
1
32
.
Proof of Claim. The previous claim implies
∂
2
∂δ
2
JS(p,q)
t
Welch
(p,q)
=
1
4
·ψ ·φ
>
1
4
·ψ ·
1
2p(1 − p)
(26)
which is equivalent to Equation (25) if we consider
the explicit form of ψ and use variance expressions.
The lower bound of
1
32
follows as under the assump-
tion 0 < q < p <
1
2
we have
Var(q) < Var

p + q
2

< Var(p) (27)
The convexity part in the lemma follows directly
from the last claim. The minimum for each q exists
because of convexity and is achieved for δ = 0, as at
this point the first derivative vanishes (see calculations
in Section 5).
5 CONCLUSION
We have studied Bayes factors in the context of A/B
testing of event rates, which is relevant to the impor-
tant problem of conversion optimization.
The result can be easily extended to cover the case
of unequal group sizes. Also it is possible to derive
bounds for testing a fixed-size effect δ instead of zero-
effect as the null hypothesis.
Finally, regarding the problem of comparing the
Welch’s t and Jensen-Shannon divergence we conjec-
ture that the inequality in Theorem 2 can be improved,
namely
Proposition 1 (Open problem). Let 0 6 q 6 p 6
1
2
.
Find the biggest constant C such that
JS(p,q) > C ·
t
Welch
(r, p,q)
2
r
(28)
The current proof is based on global convexity
which works under a subptimal constant C =
1
32
.
ACKNOWLEDGMENTS
The author thanks to Evan Miller for inspiring discus-
sions.
REFERENCES
Derrick, B., Toher, D., and White, P. (2016). Why welch’s
test is type i error robust. The Quantitative Methods
in Psychology, 12(1):30–38.
Edwards, W., Lindman, H., and Savage, L. J. (1963).
Bayesian statistical inference for psychological re-
search. Psychological Review, 70(3):193–242.
Goodman, S. N. (1999). Toward evidence-based medical
statistics. 2: The bayes factor. Annals of internal
medicine, 130 12:1005–13.
Jeffreys, H. (1998). The Theory of Probability. Oxford
Classic Texts in the Physical Sciences. OUP Oxford.
Kass, R. E. and Raftery, A. E. (1995). Bayes fac-
tors. Journal of the American Statistical Association,
90(430):773–795.
Keser, A. (2017). Goodbye, t-test: new stats models
for a/b testing boost accuracy, effectiveness. https:
//www.widerfunnel.com/goodbye-t-test-new-stats-
models-for-ab-testing-boost-accuracy-effectiveness/.
On Bayes Factors for Success Rate A/B Testing
337

Kruschke, J. K. and Liddell, T. M. (2018). The bayesian
new statistics: Hypothesis testing, estimation, meta-
analysis, and power analysis from a bayesian perspec-
tive. Psychonomic Bulletin & Review, 25(1):178–206.
Lavine, M. and Schervish, M. J. (1999). Bayes factors:
What they are and what they are not. The American
Statistician, 53(2):119–122.
Lee, M. D. and Wagenmakers, E.-J. (2014). Bayesian cog-
nitive modeling: A practical course. Cambridge uni-
versity press.
Lin, J. (1991). Divergence measures based on the shannon
entropy. IEEE Transactions on Information Theory,
37(1):145–151.
Meurer, A., Smith, C. P., Paprocki, M.,
ˇ
Cert
´
ık, O., Kir-
pichev, S. B., Rocklin, M., Kumar, A., Ivanov, S.,
Moore, J. K., Singh, S., Rathnayake, T., Vig, S.,
Granger, B. E., Muller, R. P., Bonazzi, F., Gupta, H.,
Vats, S., Johansson, F., Pedregosa, F., Curry, M. J.,
Terrel, A. R., Rou
ˇ
cka, v., Saboo, A., Fernando, I., Ku-
lal, S., Cimrman, R., and Scopatz, A. (2017). Sympy:
symbolic computing in python. PeerJ Computer Sci-
ence, 3:e103.
Morey, R. D. and Rouder, J. N. (2018). BAYESFACTOR:
computation of bayes factors for common designs. r
package version 0.9.12-4.2. http://CRAN.R-project.
org/package=BayesFactor.
Welch, B. L. (1938). The significance of the difference be-
tween two means when the population variances are
unequal. Biometrika, 29(3/4):350–362.
APPENDIX
Code
The following Python code implements the compari-
son sketched on Figure 2.
import numpy a s np
from m a t p l o t l i b import p y p l o t a s p l t
H=lambda p , q:−p ∗np . l o g ( q)−(1−p ) ∗ np . l o g (1−q )
KL=lambda p , q :H( p , q)−H( p , p )
JS=lambda p , q : ( KL( p , ( p+q ) / 2 ) + KL( q , ( p+q ) / 2 ) ) / 2
Welch=lambda p , q : ( p−q ) / np . s q r t ( p∗(1 −p )+ q∗(1 −q ) )
r b a y e s = lambda p , q : np . l o g ( 1 0 ) / ( 2 ∗ JS ( p , q ) )
r f r e q = lambda p , q : 1 . 9 ∗∗2 ∗Welch ( p , q )∗∗( −2)
p= np . l i n s p a c e ( 0 , 0 . 5 , 2 0 1 )
d e l t a = 0 . 1
q= p ∗(1+ d e l t a )
p l t . f i g u r e ( f i g s i z e = ( 1 2 , 6 ) )
p l t . p l o t ( r b a y e s ( p , q ) , \
l a b e l = ’ b a y e s i a n ( JS ) ’ )
p l t . p l o t ( r f r e q ( p , q ) , \
l a b e l = ’ f r e q u e n t i o n i s t s ( Welch−t ) ’ )
p l t . y s c a l e ( ’ l o g ’ )
p l t . x t i c k s ( np . a r a n g e ( 0 , 2 0 1 , 1 0 ) , \
np . l i n s p a c e ( 0 , 0 . 5 , 2 1 ) . round ( 3 ) )
p l t . l e g e n d ( )
p l t . y l a b e l ( ’ sa m p l e s ’ )
p l t . x l a b e l ( ’ b a s e l i n e p ’ )
p l t . show ( )
Proof of Lemma 3
Below we compute the formula in Claim 3
import sympy
p , q , d = sympy . s y m bo l s ( r ’ p q d ’ )
# d e f i n e JS and Welch ’ s t
wel c h = ( p−q ) ∗∗2 / ( p∗(1−p ) + q∗(1−q ) )
H = −p ∗sympy . l o g ( p)−(1−p ) ∗sympy . l o g (1−p )
JS = H . s u b s ( p , ( p+q ) / 2 ) − 1 / 2 ∗H − 1 / 2 ∗H . s u b s ( p , q )
# s e c o n d d e r i v a t i v e s
o u t 1 = JS . s u b s ( p , q+d ) . d i f f ( d , 2 ) . su b s ( d , p−q )
o u t 2 = wel c h . s u b s ( p , q+d ) . d i f f ( d , 2 ) . s u b s ( d , p−q )
# r a t i o o f s e c o n d d e r i v a t i v e s
( o u t 1 / o u t 2 ) . f a c t o r ( )
o u t
Below we include the code used to derive formu-
las in the proof of Claim 5
import sympy
p , q = sympy . s ym bo l s ( r ’ p q ’ )
U = ( p ∗∗2 − 2∗p∗q − q ∗∗2 + 2∗q )
V = (−2∗p ∗∗3∗q + p ∗∗3 + 3∗p ∗∗2∗q \
+6∗p∗q ∗∗3 − 9∗p ∗q ∗∗2 − 3∗q ∗∗3 + 4∗q ∗∗2 )
(U∗p ∗(1−p ) −1/2 ∗V ) . f a c t o r ( )
The following piece of code is used to validate the
claim about the global minimum at δ = 0, the end of
the proof of Lemma 3
import sympy
wel c h = ( p−q ) ∗∗2 / ( p∗(1−p ) + q∗(1−q ) )
H = −p ∗sympy . l o g ( p)−(1−p ) ∗sympy . l o g (1−p )
JS = H . s u b s ( p , ( p+q ) / 2 ) − 1 / 2 ∗H − 1 / 2 ∗H . s u b s ( p , q )
# ou t 1 = JS . s u b s ( p , q+d ) . d i f f ( d , 2 ) . s u b s ( d , p−q )
# ou t 2 = w e l c h . s u b s ( p , q+d ) . d i f f ( d , 2 ) . s u b s ( d , p−q )
# ( o u t 1 / o u t 2 ) . f a c t o r ( )
d e r i v a t i v e = ( JS −1/32∗we lc h ) . s u b s ( p , q+d ) . d i f f ( d , 1 )
d e r i v a t i v e . s u b s ( d , 0 )
The next piece of code evaluates the second
derivative in Lemma 2
H = −p ∗sympy . l o g ( p)−(1−p ) ∗sympy . l o g (1−p )
JS = H . s u b s ( p , ( p+q ) / 2 ) − 1 / 2 ∗H − 1 / 2 ∗H . s u b s ( p , q )
JS . s u b s ( p , q+d ) . d i f f ( d , 2 ) . s u b s ( d , p−q ) . f a c t o r ( )
DATA 2019 - 8th International Conference on Data Science, Technology and Applications
338

Plots
import nump y as np
from m a tp l ot l ib import pyp l o t as plt
from scip y import sp e cia l as sc
H = lambda p : -sc . x l ogy ( p , p )- sc . x logy (1 - p ,1 - p )
JS = lambda p , q : H (( p + q ) /2) -0.5* H ( p ) -0.5* H (q )
Welch = lambda p , q : np . d ivid e ((p - q ) , np . sqrt ( p *(1 - p )+ q *(1 -q )) ,
out = np . ze r os _ li k e ( p ) , wh e re = p *(1 - p )+ q *(1 - q ) >0)
p = np . lins p ace (0 ,1 ,1 0 0 + 1 )
q = np . lins p ace (0 ,1 ,1 0 0 + 1 )
xx , yy = np . me sh g rid (p , q )
zz_js =JS ( xx ,yy )
zz_ w el c h = Welc h (xx , yy )
zz = z z_w e lch
labe l s = { ’ We l c h ’: ’ $ W elch ˆ2( p_1 , p_2 ) $ ’ , ’ JS ’: ’ $JS ( p_1 , p_2 ) $ ’}
vmax = { ’ Wel c h ’ :2 , ’ JS ’ :0 . 5 }
fig = plt . figure ( fi g siz e =(1 6 ,6))
for i ,( zz , label ) in enumerate(zip([ z z _we l ch **2 , zz_j s ],
labe l s . key s () ) ) :
ax = fig . add_ sub pl o t (1 ,2 ,1+ i , proj e ct i on =’ 3 d ’)
surf = ax . plot _s u rf a ce (xx , yy , zz ,
cmap = p lt . cm . c o o l w a r m , rstr i de =1 , cst r ide =1 ,
li n ewi d th =0 , vmax = vm ax [ l abel ])
ax . se t _x l ab e l ( r " $p _ 1 $ " )
ax . se t _y l ab e l ( r " $p _ 2 $ " )
ax . se t _z l ab e l ( label s [ labe l ])
ax . zaxis . lab e lpa d =10
ax . in v er t_ x ax i s ()
fig . c olo r ba r ( surf , s hrin k =0.5 , a s pect =5)
plt . rc ( ’ a x es ’ , l abe lsi z e =15)
plt . show ()
On Bayes Factors for Success Rate A/B Testing
339