Branching Poisson Process Modelling for Reliability Analysis of
Repairable Mechanical System
Nicolas La Roche-Carrier
1
, Guyh Dituba Ngoma
1
,Yasar Kocaefe
2
and Fouad Erchiqui
1
1
School of Engineering, University of Quebec in Abitibi-T
´
emiscamingue,
445 Boulevard de l’Universit
´
e, Rouyn-Noranda, Canada
2
Department of Applied Sciences, University of Quebec in Chicoutimi, 555 Boulevard de l’Universit
´
e, Chicoutimi, Canada
Keywords:
Reliability, Modelization, Branching Poisson Process (BPP), Non-homogeneous Poisson Process (NHPP).
Abstract:
In a series of mechanical system maintenance it is possible to observe failures, sometimes intermittent, which
cause series of unsuccessful repair attempts before the correct fault is detected and the repair is effective.
Unsuccessful repairs performed for the same failure are not negligible and must be taken into account for the
reliability analysis. To solve this type of problem, the model proposed is the branching Poisson process (BPP).
This process is the representation of a primary failure that triggers one or more subsidiary failures. A summary
and an adaptation for the resolution of the branching Poisson with failures time of repairable mechanical
system were highlighted including some clarification regarding the steps of resolution implemented.
1 INTRODUCTION
The reliability is the probability of a system
performing its purpose correctly without defects
according to the given conditions within a certain
time (Barlow and Proschan, 1965). It plays an
important role in accomplishing the steps leading
to improved maintenance. The understanding of its
concepts is essential in order to model the system state
and to find an acceptable maintenance scenario. A
mechanical system is said repairable if it is possible
to restore its primitive qualities when it fails (Ascher
and Feingold, 1984). When the failure system occurs
at a specific age, maintenance is carried out to restore
its initial qualities. These maintenance actions can
affect the overall behavior of the system and involve
its operation due to variable maintenance resources
such as human errors, parts quality and preventive
action performance (Procaccia et al., 2011).
Four stochastic processes are commonly cited
to analyze the reliability of repairable system: the
renewal process (RP), the homogeneous Poisson
process (HPP), the non-homogeneous Poisson
process (NHPP) and the branching Poisson process
(BPP) (Ascher and Feingold, 1984; Garmabaki et al.,
2015). The renewal process is an arrival process
whose intermediate intervals (times of failure) are
positive, independent and identically distributed data
(Barlow and Proschan, 1965). The random feature of
the renewal process supposes that maintenance has
restored the initial primitive qualities to the system,
so that it can be considered new and the assumption
“as good as new” is applicable. With this process,
it is then possible to use conventional statistical
techniques to evaluate reliability functions. The
HPP is a particular case of the renewal process in
which the failure times are i.d.d. whose interarrival
distribution is closely related to the exponential
distribution (Tobias and Trindade, 2012). The NHPP
applies when the “as bad as old” assumption is
considered and the reliability has not been improved
since the last failure (Barlow and Hunter, 1960).
The repair action is just enough to make the system
operational again and the failure intensity function
remains the same or worse as last maintenance
before, which, over time, will degrade the integrity
of the system. The BPP is implemented when the
failure times are identically distributed but are not
independent. This article is focused on this specific
Poisson process using a case study. This process
is poorly documented in the literature on reliability
analysis : it is often referred like a milestone in
the process of analyzing failure data, but hardly
applied since it is very common that failure data are
independent.
202
Roche-Carrier, N., Ngoma, G., Kocaefe, Y. and Erchiqui, F.
Branching Poisson Process Modelling for Reliability Analysis of Repairable Mechanical System.
DOI: 10.5220/0007772302020208
In Proceedings of the 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2019), pages 202-208
ISBN: 978-989-758-381-0
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 MATHEMATICAL
FORMULATION
This section summarizes the theory and the model
adaptation of branching Poisson process from
references (Lewis, 1964a; Lewis, 1964b; Cox and
Lewis, 1966; Rigdon and Basu, 2000). In addition,
some clarifications are provided in relation with the
established model.
2.1 Branching Poisson Theory
The process is characterized by random variables
Z
1
,Z
2
,... ,Z
k
defined as the times between the
primary failures (i.e. time to the k
th
primary event)
and the random variables Y
1
,Y
1
+ Y
2
,. .. ,Y
1
+ .. . +
Y
s+1
defined as the times between the subsidiary
failures and triggered by primary failures (i.e. time
to the s
th
subsidiary event). If the term H(t) is the
expected number of subsidiary failures in the finite
renewal process, then for a time interval [0,t], the
contribution of the k
th
event in the subsidiary process
for the expected number of events is:
E
h
N
(k)
(t)
i
=
t
Z
0
H(t − z) f
k
(z)dz (1)
where f
k
(t) denote the probability density function
of primary events. In the time interval [0,t],
the expected number of failures E
h
N
(0)
(t)
i
of the
complete process is the sum of the primary failures
number and the cumulative sum of the subsidiary
failures number from the k
th
event.
E
h
N
(0)
(t)
i
= E [N(t)] +
∞
∑
k=1
E
h
N
(k)
(t)
i
= M
z
(t) +
t
R
0
H(t − z)

∞
∑
k=1
f
k
(z)

dz
(2)
where M
z
(t) is the expected number of primary events
in [0, t]. By definition:
m
z
(t) =
dM
z
(t)
dt
=
∞
∑
k=1
f
k
(t) (3)
Then, Equation (2) becomes:
E
h
N
(0)
(t)
i
= M
z
(t) +
t
Z
0
H(t − z)m
z
(t)dz (4)
If the primary process is considered a Poisson
process, then the probability density function is equal
f
z
(t) = λ exp(−λt) and the expected number of events
of the primary process becomes M
z
(t) = λt. The
expected number of events M(t) of the complete
process is thus obtained:
M(t) = E
h
N
(0)
(t)
i
= λt + λ
t
Z
0
H(t − z)dz (5)
The rate of occurrence of failures function or the
intensity function m(t) of the complete process is
defined by:
m(t) =
dM(t)
dt
= λ[1 + H(t)] (6)
If the number of subsidiary S failures is known, the
expected number of events E [H(t)
|
S] should tend to
S since all subsidiary failures are required to occur
(Rigdon and Basu, 2000). Applying the limit to H(t):
lim
t→∞
H(t) = E(S) (7)
From Equation (6), the intensity function for the
branching Poissson process is:
lim
t→∞
m(t) = lim
t→∞
λ[1 + H(t)] = λ [1 + E(S)] (8)
2.2 Branching Poisson Modelling
The principle of the branching Poisson modelling
is to represent the main process from occurrence
of the primary failures and the process from
occurrence of the subsidiary failures, which is
dependent on the main process. Some probability
functions are applicable to modeling the first order
of branching Poisson like the exponential and the
gamma distributions. The objective is to compare the
empirical reliability function R
n
0
with the theoretical
data modeled by the reliability function R
T
(t), which
defines the branching Poisson process. Validation
of the model adopted are done by comparing the
reliability functions on a logarithmic scale (Lewis,
1964a). The logarithmic definition of empirical
reliability function R
n
0
of i for the i
th
failure is:
lnR
n
0
(i) = ln

1 −
i
n
0
+ 1

(9)
where n
o
is the number of failures. According to
the branching Poisson process, the reliability function
R
T
(t) of the time between failure t
i
is given by:
R
T
(t) =
[1 + aR
Y
(t)]
(1 + a)
· E
1
where
E
1
= exp

−λt − λa
t
R
0
R
Y
(u)du

(10)
Branching Poisson Process Modelling for Reliability Analysis of Repairable Mechanical System
203

where R
Y
(t) is the reliability function of the
subsidiary process (exponential or gamma) and the
parameter a = E(S) is the expected number of
subsidiary failures. The probability density function
f
T
(t) of the branching Poisson process is defined by:
f
T
(t) =

λ + a f
Y
(t) + 2λaR
Y
(t) + λa
2
R
2
Y
(t)

(1 + a)
· E
1
(11)
where f
Y
(t) is the probability density function of the
subsidiary process. For a time t  E(Y ), R
Y
(t) → 0
and
t
R
0
R
Y
(u)du → E(Y ) (Karyagina et al., 1998).
By substituting b = E(Z)

E(Y ) = 1

{
λE(Y )
}
and
applying the logarithm to the reliability function
R
T
(t) from equation (10), the next equation is formed:
lnR
T
(t) ≈ ln(1 + a) −
a
b
− λt (12)
The term λ is estimated as the slope of the straight
line on the tail of the distribution lnR
n
0
(i) (if the
slope is obvious for the sample). The tail of the
distribution is defined from the point of truncation,
i.e. where there is a decrease in the occurrence
of subsidiary failures data. This truncation point is
arbitrary and is determined with the values generated
with Equation (9). The term a is according to the
intensity function from Equation (8):
a =
E(Z)
E(T )
− 1 (13)
where E(T ) is the expected value of the interarrival
times t and E(Z) = 1

λ is the expected value of the
times adjusted to the tail of the distribution lnR
n
0
(i).
If the term a is small (a < 1), then the resulting
curve will be very close to the logarithm of the
homogeneous Poisson distribution (Karyagina et al.,
1998). The term b of Equation (12) is the intercept of
line fitted to the tail of the distribution ln R
n
0
(i). The
expected value E(Y ) for the subsidiary distribution
{Y
i
} is given by:
E(Y ) =
E(Z)
b
(14)
The failure rate z
T
(t) of the branching Poisson
process is the ratio of the probability density function
on the reliability function.
z
T
(t) =
f
T
(t)
R
T
(t)
(15)
The probability density function f
Y
(t) for the
exponential function is:
f
Y
(t) = βexp(−βt) (16)
where β = 1

E(Y ) is the intensity parameter.
Determined from the integral of f
Y
(t), the reliability
function of the subsidiary process R
Y
(t) for the
exponential function is:
R
Y
(t) = exp(−βt) (17)
From Equations (10) and (17), the logarithm of the
reliability function for an exponential function R
T
(t)
is given by :
lnR
T
(t) = ln

[1 + a exp(−βt)]
(1 + a)
· E
2

where
E
2
= exp

−λt − λa

1 − exp(−βt)
β

(18)
If the choice of the distribution for {Y
i
} is a gamma
function, then the probability density function f
Y
(t)
is (Hogg and Craig, 1978):
f
Y
(t) =
β
k
t
k−1
exp(−βt)
Γ(k)
(19)
where Γ is the gamma function, β = k

E(Y ) is the
intensity parameter and k is the shape parameter.
The cumulative distribution function F
Y
(t) of gamma
function is defined by (Abramowitz and Stegun,
1972):
F
Y
(t) =
1
Γ(k)
t
Z
0
h
(βt)
(k−1)
exp(−βt)
i
dt (20)
If the parameter k is a strictly positive integer, then the
cumulative distribution function follows the Erlang
distribution (Papoulis, 1991):
F
Y
(t) = 1 − exp(−βt)
k−1
∑
υ=0

(βt)
υ
υ!

(21)
The reliability R
Y
(t) for the gamma distribution is:
R
Y
(t) = 1 − F
Y
(t) = exp(−βt)
k−1
∑
υ=0

(βt)
υ
υ!

(22)
From Equations (10) and (22), the model adapted to
a logarithm reliability function for a gamma function
R
T
(t) is given by:
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
204

lnR
T
(t) = ln





1 + a exp(−βt)
k−1
∑
υ=0

(βt)
υ
υ!

(1 + a)
· E
3




where
E
3
= exp

−λt − ab

1 − exp

−
kt
E(Y )

· E
4

E
4
=
k−1
∑
υ=0

t
E(Y )

υ
k
υ−1
(k − υ)
υ!

(23)
3 RELIABILITY ANALYSIS
PROCESS
In the reliability analysis process for reparable
system, the first step is to verify if the independence
hypothesis of the failure data is respected. If
the hypothesis validation is not confirmed then
classical statistical techniques cannot be applied and
it is necessary to use the non-homogeneous Poisson
process (Ascher and Feingold, 1984). Independent
data implies that there is no trend: each failure
is independent of the previous or the next failure.
Identical distributions indicate that data come from
the same probability distribution. If the process is
free of trends, the application of the dependency
test will specify whether the data follow a renewal
process or a branching Poisson process. The detection
and the anlalysis of dependency can be realized with
the correlation coefficient (Lewis, 1964a). If there
is acceptance of the hypothesis which accepts the
existence of correlation between data, it is possible to
model the failures by the branching Poisson process.
The process to analyze the reliability of repairable
system with applicable tests is presented in Figure 1.
3.1 Trend and Dependence Tests
After the collection, sorting and classification of
the chronological failures data, the trend evolution
can be examined with hypothesis testing methods.
Since some trend tests have a greater sensitivity
to the number of events, it is preferable to
apply different investigations to validate the same
assumption of resolution. In this study, the Laplace
test and Military Handbook test (MIL-HDBK-189)
are effective hypothesis methods to validate the null
hypothesis of homogenous Poisson process (HPP), in
order to verify non-trend behavior. The Laplace test
compares the mean value of the observed data with
the midpoint of the interval and a trend is observed
Database
Trend ?
Laplace Test
MIL-HDBK-189 Test
Non-Homogeneous
Poisson Process (NHPP)
Crow/AMSAA model
Goodness of Fit
Cram
´
er-von Mises Test
Dependance ?
Pearson Correlation Test
Branching Poisson
Process (BPP)
Renewal Process (RP)
Independent and Identically
Distributed Data
Choosing a
Proability Distribution
Goodness of Fit
Acceptance as
Probability Distribution
Constant failure rate ?
Homogeneous
Poisson Process (HPP)
Reliability and maintenance analysis
yes
no
yes
no
no
yes
Figure 1: Reliability analysis process (adapted from Ascher
and Feingold, 1984).
in the data when the mean value of the failure time
moves away from the central point. The Laplace
test statistic criterion for testing H
0
(HPP) against
H
1
(NHPP) is based on the normality of the variable
Z
L
with the significance level α. The test, with the
number of failures ˆn, the occurrence of failures time t
i
and the time interval of observation [T
a
, T
b
], is given
by (Kvaløy and Lindqvist, 1998):
Z
L[T
a
,T
b
]
=
ˆn
∑
i=1
t
i
−
1
2
ˆn(T
b
+ T
a
)
(T
b
− T
a
)
q
ˆn

12
(24)
The MIL-HDBK-189 test compares a null
hypothesis test H
0
associated to a HPP against
the alternative hypothesis H
1
associated to a NHPP
(U.S. Department of Defense, 1981). The test is
distributed according to a chi-squared distribution
with 2 ˆn degree of freedom with the significance level
α. The statistic with the number of failures ˆn and the
occurrence of failures time t
i
, is defined for a time
interval of observation [T
a
, T
b
] as follows (Stephens,
2012):
MH = 2
ˆn
∑
i=1
ln

T
b
− T
a
t
i
− T
a

(25)
When the situation gives opposite hypothesis
validation for the trend tests, then the Cram
´
er-von
Mises goodness-of-fit test can be used to confirm
Branching Poisson Process Modelling for Reliability Analysis of Repairable Mechanical System
205

the assumption for the trend. This test verifying the
null hypothesis H
0
associated to a NHPP against the
alternative hypothesis H
1
associated to a rejection of
NHPP and when the statistic’s value C
2
M
is greater
than the critical value, then the hypothesis H
0
is
rejected at the significance level α chosen. This
statistic is expressed in this form (Crow, 1990):
C
2
M
=
1
12M
+
M
∑
i=1

Z
i
¯
β
−
(2i − 1)
2M

2
(26)
where M = n, Z
i
= t
i
/T , T is the total time on the test,
β is the shape parameter from the NHPP, defined by
the power law model (Rigdon and Basu, 2000):
β =
n − 1
n
∑
i=1
ln

T
t
i

(27)
The dependency between observed data can be found
by the correlation test. In this paper, the numerical
analysis of the dependence is given with the Pearson
correlation coefficient (Cox and Lewis, 1966).
r
k
=
Cov(X
i
,X
i+k
)
Var(X)
(28)
where k is the time lag, Var(X) is the variance of the
X, Cov(X, X
i+k
), σ(X
i
) and σ(X
i+k
) are respectively
the covariance and the standard deviations of
the quantitative variables X
i
et X
i+k
. The test
rejection criterion is based on the null hypothesis
H
0
which admits an absence of correlation and the
alternative hypothesis H
1
which admits the existence
of correlation. The test calculating the variable t
0
and
comparing it to the value of the significance level α
from the Student’s t-distribution (Vaurio, 1999).
4 RESULTS AND DISCUSSION
4.1 Data Collection
The data selected come from a mechanical repairable
system of Load-Haul-Dump vehicle, more precisely
from the powertrain system (transmission, parking
brakes, gear box, drive lines front axle and rear
axle), and represented by the recorded time between
failures (TBF). These failures can be examined and
evaluated for the applicability of the BPP. In some
industrial context, it is not possible to take the failure
data since the beginning of the procedure: a series of
events was taken between two times of the system
operation. The initial time interval T
a
corresponds to
the first observation time of failure. Since the failures
are censored by time, the time T
b
corresponds to the
final recording time. Table 1 shows the failures time
and the operating age range.
Table 1: Time between failures.
n
o
t
i
(h) n
o
t
i
(h)
1 11 977 16 13 820
2 12 450 17 13 867
3 12 513 18 13 917
4 12 654 19 14 042
5 12 844 20 14 075
6 13 066 21 14 240
7 13 155 22 14 560
8 13 280 23 14 933
9 13 380 24 15 275
10 13 394 25 15 369
11 13 440 26 15 635
12 13 479 27 16 625
13 13 515 28 16 729
14 13 525 29 17 380
15 13 605 30 17 400
T = T
b
18 000
4.2 Analysis of Times Between Failures
The failures trend was validated with three methods:
the Laplace test, the Military Handbook test
(MIL-HDBK-189) and the Cram
´
er-von Mises test.
Table 2 illustrates the trend tests performed on failures
data. It is possible to notice that the null hypothesis
H
0
which admits a homogeneous Poisson process
is rejected by the Laplace test, but accepted by the
Military Handbook test. With the application of
the third test, the Cram
´
er-von Mises goodness-of-fit
test, it is possible to settle on this dilemma. The
execution of this last test demonstrates that the null
hypothesis H
0
is rejected, which admits a rejection
of the non-homogeneous Poisson process. Then, the
results favor the assumption that failures data are
without trend and identically distributed.
The next step is the correlation verification
between failures. The dependency test was calculated
with a two lag parameters (k = 1 and k = 2) and the
correlation coefficients maximum between r
1
and r
2
was considered.
By analyzing the test results shown in Table 3, it
is obvious that the null hypothesis H
0
which admits a
lack of correlation (r = 0) is rejected since the value
of t
0
is greater than the citrical value. In this case,
failures data follow a BPP.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
206

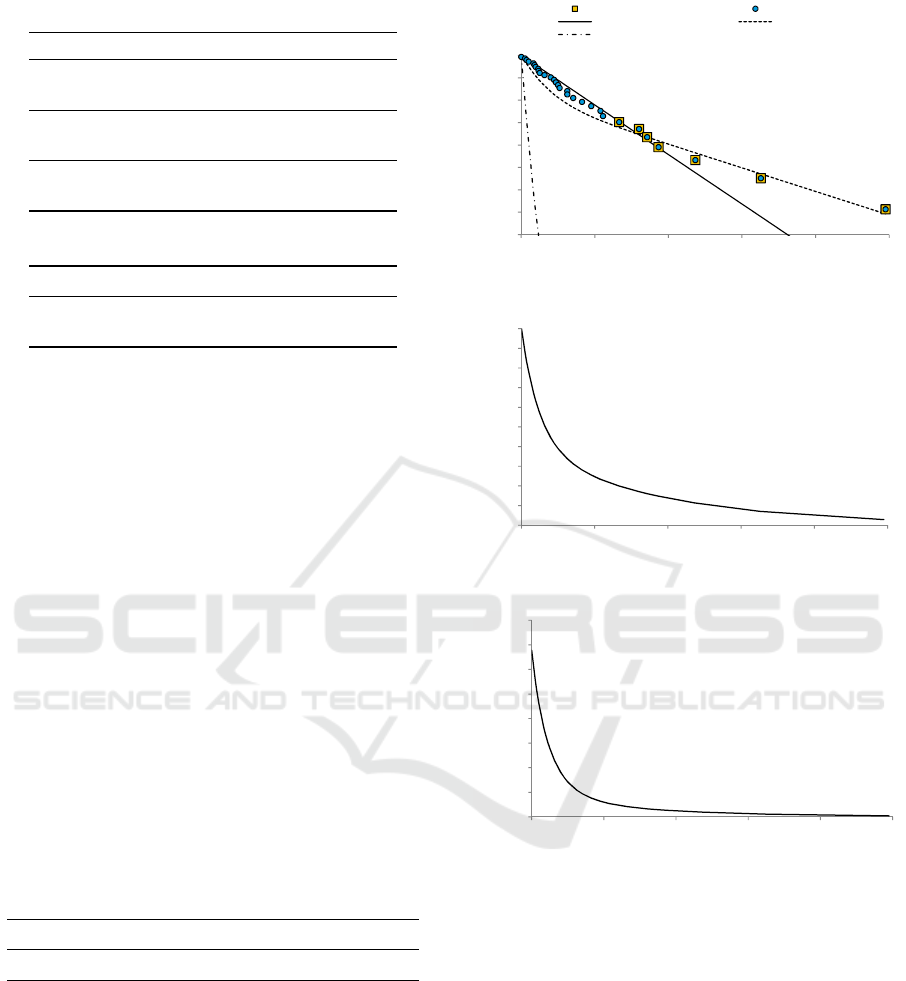
Table 2: Computed value for trend tests.
Rejection of null hypothesis H
0
at 5 % level of significance
Laplace Rejected p-value
(-2.68 < -1.96) 0.007
MIL-HDBK-189 Not rejected p-value
(79.08 > 68.45 > 43.19) 0.788
Cram
´
er–von Mises Rejected
(0.642 > 0.217)
Table 3: Computed value for dependency test.
Rejection of null hypothesis H
0
at 5 % level of significance
r
1
r
2
p-value Rejected
0.04 0.38 0.04 (0.219 > 0.205)
4.3 Application of the BPP
The definition of the failure intensity depends on
the subsidiary distribution {Y
i
} and the distribution
S. With some initial assumptions, the distribution
of {Y
i
} and the parameters associated with the BPP
can be estimated from the failure data. As seen
in Figure 2, the chart of the logarithmic reliability
function ln R
T
(t) was done initially with the plotting
of the empirical values represented by the function
from equation (9). From these empirical values, the
tail of the distribution has been defined from the
point truncation, chosen arbitrarily. The truncation
point was selected at interarrival time t = 250 h from
where there is a decrease on the number of events
representing the subsidiary failures. This new plot is
represented by the tail distribution on the chart. With
the tail distribution line, it is possible to estimate the
parameters from the branching Poisson model. The
main parameters of the BPP model, like expected
values from processes, are available in Table 4.
Table 4: Parameters estimation of BPP.
λ [slope] Intercept E(Z) a b E(Y ) β
0.00263 -0.9308 380 1.1 5.82 65 0.01533
Then, the logarithm of the reliability from BPP
model, according to the exponential and gamma
distributions (k = 2), was calculated and represented
on Figure 2. Also, it has been added the curve of
the reliability function represented by HPP model.
As shown in Figure 2, it is obvious that the gamma
distribution applied to the BPP model does not fit well
with failures data. Moreover, since the curve lnR
T
(t)
is concave upward, it is possible to rule out the gamma
function (k > 1) for the distribution of {Y
i
} (Lewis,
1964a).
-4
-3,5
-3
-2,5
-2
-1,5
-1
-0,5
0
0 200 400 600 800 1000
lnR
T
(t)
Interarrival times
Tail Distribution
ln(Rn0)
ln(RT) [HPP]
ln(RT) [BPP
-
Exp.]
ln(RT) [BPP
-
Gamma]
Figure 2: Log survivor of reliability function.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 200 400 600 800 1000
R
T
(t)
Interarrival times
Figure 3: Reliability function of BPP model.
0,000
0,002
0,004
0,006
0,008
0,010
0,012
0,014
0,016
0 200 400 600 800 1000
f
T
(t)
Interarrival times
Figure 4: Probability density function of BPP model.
In this case study, the branching Poisson process
with an exponential distribution is the best model
according to failures data. Figures 3 and 4 present
respectively the reliability function R
T
(t) and the
probability density function f
T
(t) modeling the BPP
process from the reparable mechanical system.
The smaller value of E(Y ) compared to mean
between failures 1/λ of the main process is
consistent: before the source of the system failure
is located and adequately repaired, there is a
probability that unsuccessful maintenance events can
reduce system operation after attempting a failure
repair. Calculated by the parameter a, the higher
intensity function from the mechanical system could
be predominantly due to a series of imperfect
Branching Poisson Process Modelling for Reliability Analysis of Repairable Mechanical System
207

repairs. For this case, it is better to wait for more
maintenance data to validate if an improvement from
the mechanical system is visible and validate if the
stochastic process that defines the failures is then
a renewal process. Otherwise, it will be necessary
to consider modifying the maintenance policy by
implementing more preventive action in order to
follow up and repair the state of the system. However,
beyond the reality of imperfect maintenance, the
correlation between data can come from anomalies
may be related to insufficient data collection or other
situations not representative of the failure process.
5 CONCLUSION
In this study, the reliability and the probability density
from repairable mechanical system were evaluated.
The correlation test accepts the assumption of
dependency for failures data and thereby, they follow
a branching Poisson process. This process could
be modeled from the graph based on a logarithmic
scale and the equations defined in mathematical
formulation section. For practical purposes, the
estimated parameters of first order properties from
the modeling are sufficient to give an interpretation
of the branching process Poisson followed by the
failure data. Given the verification of the Branching
Poisson process model from the mechanical system,
the interest remains in the value of the failure rate λ
and the efficiency of the system repair E(S). Then,
the main utility of the branching Poisson process is
that it can be used to give a physical interpretation of
the deviation for the time between failures.
ACKNOWLEDGMENT
The authors are grateful to support of the Natural
Sciences and Engineering Research Council of
Canada (NSERC) and the Fonds de recherche du
Qu
´
ebec - Nature et technologies (FRQNT).
REFERENCES
Abramowitz, M. and Stegun, I. (1972). Handbook of
Mathematical Functions with Formulas, Graphs, and
Mathematical Tables. U.S. Government Printing
Office, Washington, D.C.
Ascher, H. and Feingold, H. (1984). Repairable System
Reliability: Modeling, Inference, Misconceptions and
Their Cause. Marcel Dekker, New York.
Barlow, R. E. and Hunter, L. (1960). Optimum preventive
maintenance policies. Operations research,
8(1):90–100.
Barlow, R. E. and Proschan, F. (1965). Mathematical
Theory of Reliability. Wiley, New York.
Cox, D. and Lewis, P. A. W. (1966). The Statistical Analysis
of Series of Events. Chapman and Hall, London.
Crow, L. H. (1990). Evaluating the reliability of
repairable systems. In Reliability and Maintainability
Symposium, 1990, pages 275–279, Los Angeles,
USA. IEEE.
Garmabaki, A., Ahmadi, A., Mahmood, Y. A., and
Barabadi, A. (2015). Reliability modelling of multiple
repairable units. Quality and Reliability Engineering
International, 32(7):2329–2343.
Hogg, R. and Craig, A. (1978). Introduction to
Mathematical Statistics. MacMillan, New York, 4th
edition.
Karyagina, M., Wong, W., and Vlacic, L. (1998).
Life cycle cost modelling using marked point
processes. Reliability Engineering & System Safety,
59(3):291–298.
Kvaløy, J. T. and Lindqvist, B. H. (1998). TTT-based
tests for trend in repairable systems data. Reliability
Engineering & System Safety, 60(1):13–28.
Lewis, P. A. W. (1964a). A branching Poisson process
model for the analysis of computer failure patterns.
Journal of the Royal Statistical Society. Series B
(Methodological), pages 398–456.
Lewis, P. A. W. (1964b). Implications of a failure model
for the use and maintenance of computers. Journal of
Applied Probability, 1(02):347–368.
Papoulis, A. (1991). Probability, Random Variables, and
Stochastic Processes. McGraw-Hill, New York, 3rd
edition.
Procaccia, H., Ferton, E., and Procaccia, M. (2011).
Fiabilit
´
e et maintenance des mat
´
eriels industriels
r
´
eparables et non r
´
eparables. Lavoisier, Paris.
Rigdon, S. and Basu, A. (2000). Statistical Methods for the
Reliability of Repairable Systems. Wiley, New York.
Stephens, K. (2012). Reliability Data Analysis with Excel
and Minitab. ASQ Quality Press, Milwaukee.
Tobias, P. A. and Trindade, D. C. (2012). Applied
Reliability. CRC Press, Boca Raton, 3rd edition.
U.S. Department of Defense (1981). Military Handbook,
Reliability Growth Management (MIL-HDBK-189).
U.S. Government Printing Office.
Vaurio, J. (1999). Identification of process and
distribution characteristics by testing monotonic and
non-monotonic trends in failure intensities and hazard
rates. Reliability Engineering & System Safety,
64(3):345–357.
SIMULTECH 2019 - 9th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
208