Lazy Agents for Large Scale Global Optimization
Joerg Bremer
1
and Sebastian Lehnhoff
2
1
Department of Computing Science, University of Oldenburg, Uhlhornsweg, Oldenburg, Germany
2
R&D Division Energy, OFFIS – Institute for Information Technology, Escherweg, Oldenburg, Germany
Keywords:
Global Optimization, Distributed Optimization, Multi-agent Systems, Lazy Agents, Coordinate Descent
Optimization.
Abstract:
Optimization problems with rugged, multi-modal Fitness landscapes, non-linear problems, and derivative-free
optimization entails challenges to heuristics especially in the high-dimensional case. High-dimensionality
also tightens the problem of premature convergence and leads to an exponential increase in search space
size. Parallelization for acceleration often involves domain specific knowledge for data domain partition or
functional or algorithmic decomposition. We extend a fully decentralized agent-based approach for a global
optimization algorithm based on coordinate descent and gossiping that has no specific decomposition needs
and can thus be applied to arbitrary optimization problems. Originally, the agent method suffers from likely
getting stuck in high-dimensional problems. We extend a laziness mechanism that lets the agents randomly
postpone actions of local optimization and achieve a better avoidance of stagnation in local optima. The
extension is tested against the original method as well as against established methods. The lazy agent approach
turns out to be competitive and often superior in many cases.
1 INTRODUCTION
Global optimization of non-convex, non-linear prob-
lems has long been subject to research (B
¨
ack et al.,
1997; Horst and Pardalos, 1995). Approaches can
roughly be classified into deterministic and proba-
bilistic methods. Deterministic approaches like inter-
val methods (Hansen, 1980), Cutting Plane methods
(Tuy et al., 1985), or Lipschitzian methods (Hansen
et al., 1992) often suffer from intractability of the
problem or getting stuck in local optima (Simon,
2013). In case of a rugged fitness landscape of multi-
modal, non-linear functions, probabilistic heuristics
are indispensable. Often derivative free methods are
needed, too.
Many optimization approaches have so far been
proposed for solving these problems; among them
are evolutionary methods or swarm-based methods
(B
¨
ack et al., 1997; Dorigo and St
¨
utzle, 2004; Simon,
2013; Hansen, 2006; Kennedy and Eberhart, 1995;
Storn and Price, 1997). In (Bremer and Lehnhoff,
2017a), an agent-based methods has been proposed
with the advantaged of good scaling properties as with
each new objective dimension an agent is added lo-
cally searching along the respective dimension (Bre-
mer and Lehnhoff, 2017a). The approach uses the
COHDA protocol (Hinrichs et al., 2013). In this ap-
proach, the agents perform a decentralized block co-
ordinate descent (Wright, 2015) and self-organized
aggregate locally found optima to an overall solution.
In (Hinrichs and Sonnenschein, 2014; Anders
et al., 2012), the effect of communication delays in
message sending and the degree of variation in such
agent systems on the solution quality has been scru-
tinized. Increasing variation (agents with different
knowledge interact) leads to better results. An in-
crease in inter-agent variation can also be achieved
by letting agents delay individual decisions. Hence,
we combine the ideas from (Bremer and Lehnhoff,
2017a) and (Hinrichs and Sonnenschein, 2014) and
extend the agent approach to global optimization by
integrating a decision delay into the agents. In this
way, the agents sort of behave lazy with regard to their
decision duty.
Agents in the COHDA protocol act after the
receive-decide-act metaphor (Hinrichs et al., 2013).
When applied to local optimization, the decide pro-
cess decides locally on the best parameter position
with regard to just one respective dimension of the
objective function. Thus, the agent performs a 1-
dimensional optimization along an intersection of the
objective function and takes the other dimensions (his
72
Bremer, J. and Lehnhoff, S.
Lazy Agents for Large Scale Global Optimization.
DOI: 10.5220/0007571600720079
In Proceedings of the 11th International Conference on Agents and Artificial Intelligence (ICAART 2019), pages 72-79
ISBN: 978-989-758-350-6
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

belief on the other agent’s local optimizations) as
fixed for the moment. We extend this approach by a
mechanism that postpones the decision process. Thus
the agent gathers more information from other agents
(including transient ones with more communication
hops) and may decide on a more solid basis.
The rest of the paper is organized as follows. Af-
ter a brief recap of (large scale) global optimization,
heuristics, and the agent approach for solving, the ex-
tension of laziness to the agents is explained. The
effectiveness is demonstrated by comparing with the
original approach and with standard algorithms.
2 RELATED WORK
Global optimization comprises many problems in
practice as well as in the scientific community. These
problems are often hallmarked by presence of a
rugged fitness landscape with many local optima and
non-linearity. Thus optimization algorithms are likely
to become stuck in local optima and guaranteeing the
exact optimum is often intractable; leading to the use
of heuristics.
Evolution Strategies (Rechenberg, 1965) for ex-
ample have shown excellent performance in global
optimization especially when it comes to complex
multi-modal, high-dimensional, real valued problems
(Kramer, 2010; Ulmer et al., 2003). Each of these
strategies has its own characteristics, strengths and
weaknesses. A common characteristic is the genera-
tion of an offspring solution set by exploring the char-
acteristics of the objective function in the immediate
neighborhood of an existing set of solutions. When
the solution space is hard to explore or objective eval-
uations are costly, computational effort is a common
drawback for all population-based schemes. Real
world problems often face additional computational
efforts for fitness evaluations; e. g. in Smart Grid load
planning scenarios, fitness evaluation involves simu-
lating a large number of energy resources and their
behaviour (Bremer and Sonnenschein, 2014).
Especially in high-dimensional problems, prema-
ture convergence (Leung et al., 1997; Trelea, 2003;
Rudolph, 2001) entails additional challenges onto the
used optimization method. Heuristics often converge
too early towards a sub-optimal solution and then get
stuck in this local optimum. This might for instance
happen if an adaption strategy decreases the mutation
range and thus the range of the currently searched sur-
rounding sub-region and possible ways out of a cur-
rent trough are no longer scrutinized.
On the other hand, much effort has been spent
to accelerate convergence of these methods. Ex-
ample techniques are: improved population initial-
ization (Rahnamayan et al., 2007), adaptive popula-
tions sizes(Ahrari and Shariat-Panahi, 2015) or ex-
ploiting sub-populations (Rigling and Moore, 1999).
Sometimes a surrogate model is used in case of com-
putational expensive objective functions (Loshchilov
et al., 2012) to substitute a share of objective function
evaluations with cheap surrogate model evaluations.
The surrogate model represents a learned model of
the original objective function. Recent approaches
use Radial Basis Functions, Polynomial Regression,
Support Vector Regression, Artificial Neural Network
or Kriging (Gano et al., 2006); each approach with in-
dividual advantages and drawbacks.
Recently, the number of large scale global op-
timizations problems grows as technology advances
(Li et al., 2013). Large scale problems are dif-
ficult to solve for several reasons (Weise et al.,
2012). The main reasons are the exponentially grow-
ing search space and a potential change of an ob-
jective function’s properties (Li et al., 2013; Weise
et al., 2012; Shang and Qiu, 2006). Moreover, eval-
uating large scale objectives is expensive, especially
in real world problems (Sobieszczanski-Sobieski and
Haftka, 1997). Growing non-separability or variable
interaction sometimes entail further challenges (Li
et al., 2013).
For faster execution, different approaches for par-
allel problem solving have been scrutinized in the
past; partly with a need for problem specific adaption
for distribution. Four main questions define the de-
sign decisions for distributing a heuristic: which in-
formation to exchange, when to communicate, who
communicates, and how to integrate received infor-
mation (Nieße, 2015; Talbi, 2009). Examples for
traditional meta-heuristics that are available as dis-
tributed version are: Particle swarm (Vanneschi et al.,
2011), ant colony (Colorni et al., 1991), or parallel
tempering (Li et al., 2009). Distribution for gaining
higher solution accuracy is a rather rare use case. An
example is given in (Bremer and Lehnhoff, 2016).
Another class of algorithms for global optimiza-
tion that has been popular for many years by prac-
titioners rather than scientists (Wright, 2015) is that
of coordinate descent algorithms (Ortega and Rhein-
boldt, 1970). Coordinate descent algorithms itera-
tively search for the optimum in high dimensional
problems by fixing most of the parameters (compo-
nents of variable vector x
x
x) and doing a line search
along a single free coordinate axis. Usually, all com-
ponents of x
x
x a cyclically chosen for approximating the
objective with respect to the (fixed) other components
(Wright, 2015). In each iteration, only a lower dimen-
sional or even scalar sub-problem has to be solved.
Lazy Agents for Large Scale Global Optimization
73

The multi-variable objective f (x
x
x) is solved by looking
for the minimum in one direction at a time. There
are several approaches for choosing the step size for
the step towards the local minimum, but as long as
the sequence f (x
x
x
0
), f (x
x
x
1
),... , f (x
x
x
n
) is monotonically
decreasing the method converges to an at least local
optimum. Like any other gradient based method this
approach gets easily stuck in case of a non-convex
objective function.
In (Hinrichs et al., 2013) an agent based approach
has been proposed as an algorithmic level decomposi-
tion scheme for decentralized problem solving (Talbi,
2009; Hinrichs et al., 2011), making it especially suit-
able for large scale problems.
Each agent is responsible for one dimension of
the objective function. The intermediate solutions for
other dimensions (represented by decisions published
by other agents) are regarded as temporarily fixed.
Thus, each agent only searches along a 1-dimensional
cross-section of the objective and thus has to solve
merely a simplified sub-problem. Nevertheless, for
evaluation of the solution, the full objective function
is used. In this way, the approach achieves an asyn-
chronous coordinate descent with the ability to escape
local minima by parallel searching different regions of
the search space. The approach uses as basis a proto-
col from (Hinrichs et al., 2013).
In (Hinrichs et al., 2013) a fully decentralized
agent-based approach for combinatorial optimization
problems has been introduced. Originally, the combi-
natorial optimization heuristics for distributed agents
(COHDA) had been invented to solve the problem of
predictive scheduling (Sonnenschein et al., 2014) in
the Smart Grid.
The key concept of COHDA is an asynchronous
iterative approximate best-response behavior, where
each participating agent – originally representing a
decentralized energy unit – reacts to updated informa-
tion from other agents by adapting its own action (se-
lect an energy production scheme that enables group
of energy generators to fulfil an energy product from
market as good as possible). All agents a
i
∈ A initially
only know their own respective search space S
i
of fea-
sible energy schedules that can be operated by the
own energy resource. From an algorithmic point of
view, the difficulty of the problem is given by the dis-
tributed nature of the system in contrast to the task of
finding a common allocation of schedules for a global
target power profile.
Thus, the agents coordinate by updating and ex-
changing information about each other. For privacy
and communication overhead reasons, the potential
flexibility (alternative actions) is not communicated
as a whole by an agent. Instead, the agents communi-
cate single selected local solutions (energy production
schedules in the Smart Grid case) within the approach
as described in the following.
First of all, the agents are placed in an artificial
communication topology based on the small-world
scheme, (e. g. a small world topology (Watts and Stro-
gatz, 1998), such that each agent is connected to a
non-empty subset of other agents. This overlay topol-
ogy might be a ring in the least connected variant.
Each agent collects two distinct sets of informa-
tion: on the one hand the believed current configu-
ration γ
i
of the system (that is, the most up to date
information a
i
has about currently selected schedules
of all agents), and on the other hand the best known
combination γ
∗
i
of schedules with respect to the global
objective function it has encountered so far.
Beginning with an arbitrarily chosen agent by
passing it a message containing only the global ob-
jective (i. e. the target power profile), each agent re-
peatedly executes the three steps perceive, decide, act
(cf. (Nieße et al., 2014)):
Algorithm 1: Basic scheme of an agent’s decision on local
optima in the extension of COHDA to global optimization.
1: // let x
x
x ∈ R
d
an intermediate solution
2: x
k
←
(
x
k
if x
k
∈ K
a
j
x ∼ U(x
min
,x
max
) else
∀k 6= j
3: // solve with Brent optimizer:
4: x
j
← argmin f
j
(x) = f (x,x
x
x) =
f (x
1
,.. . , x
j−1
,x, x
j+1
,.. . , x
d
)
5: if f (x
x
x) < f (x
x
x
old
) then
6: update workspace K
j
7: end if
1. perceive: When an agent a
i
receives a mes-
sage κ
p
from one of its neighbors (say, a
p
), it
imports the contents of this message into its own
memory.
2. decide: The agent then searches S
i
for the best
own local solution regarding the updated system
state γ
i
and the global objective function. Local
constraints are taken into account in advance if
applicable. Details regarding this procedure have
been presented in (Nieße et al., 2016). If a local
solution can be found that satisfies the objective, a
new solution selection is created. For the follow-
ing comparison, only the global objective function
must be taken into account: If the resulting mod-
ified system state γ
i
yields a better rating than the
current solution candidate γ
∗
i
, a new solution can-
didate is created based on γ
i
. Otherwise the old
solution candidate still reflects the best combina-
tion regarding the global objective, so the agent
reverts to its old selection stored in γ
∗
i
.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
74

3. act: If γ
i
or γ
∗
i
has been modified in one of the
previous steps, the agent finally broadcasts these
to its immediate neighbors in the communication
topology.
During this process, for each agent a
i
, its observed
system configuration γ
i
as well as solution candidate
γ
∗
i
are filled successively. After producing some in-
termediate solutions, the heuristic eventually termi-
nates in a state where for all agents γ
i
as well as γ
∗
i
are identical, and no more messages are produced by
the agents. At this point, γ
∗
i
is the final solution of the
heuristic and contains exactly one schedule selection
for each agent.
The COHDA protocol has meanwhile been ap-
plied to many different optimization problems (Bre-
mer and Lehnhoff, 2017b; Bremer and Lehnhoff,
2017c). In (Bremer and Lehnhoff, 2017a) COHDA
has also been applied to the continuous problem of
global optimization.
3 LAZY COHDAGO
In (Bremer and Lehnhoff, 2017a) the COHDA pro-
tocol has been applied to global optimization (CO-
HDAgo). Each agent is responsible for solving one
dimension x
i
of a high-dimensional function f (x
x
x) as
global objective. Each time an agent receives a mes-
sage from one of its neighbors, the own knowledge-
base with assumptions about optimal coordinates x
x
x
∗
of the optimum of f (with x
x
x
∗
= argmin f (x
x
x)) is up-
dated. Let a
j
be the agent that just has received a
message from agent a
i
. Then, the workspace K
j
of
agent a
j
is merged with information from the received
workspace K
i
. Each workspace K of an agent con-
tains a set of coordinates x
k
such that x
k
reflects the
kth coordinate of the current solution x
x
x so far found
from agent a
k
. Additionally, information about other
coordinates x
k
1
,.. . , x
k
n
reflecting local decisions of
a
k
1
,.. . , a
k
n
that a
i
has received messages from is also
integrated into K
j
if the information is newer or out-
dates the already known. Thus each agent gathers also
transient information; finally about all local decisions.
In general, each coordinate x
`
that is not yet
in K
j
is temporarily set to a random value x
`
∼
U(x
min
,x
max
) for objective evaluation. W.l.o.g. all
unknown values could also be set to zero. But, as
many of the standard benchmark objective function
have their optimum at zero, this would result in an un-
fair comparison as such behavior would unintention-
ally induce some priori knowledge. Thus, we have
chosen to initialize unknown values with a random
value.
perceive:
update knowledge
act:
send workspace
𝑎
2
𝑎
3
𝑎
1
𝑎
5
𝑎
4
Κ
𝑖
Κ
𝑗
integrate
Κ
𝑗
subset of 1-
dimensinal
solutions
decide:
optimize sub-problem
𝑎
𝑗
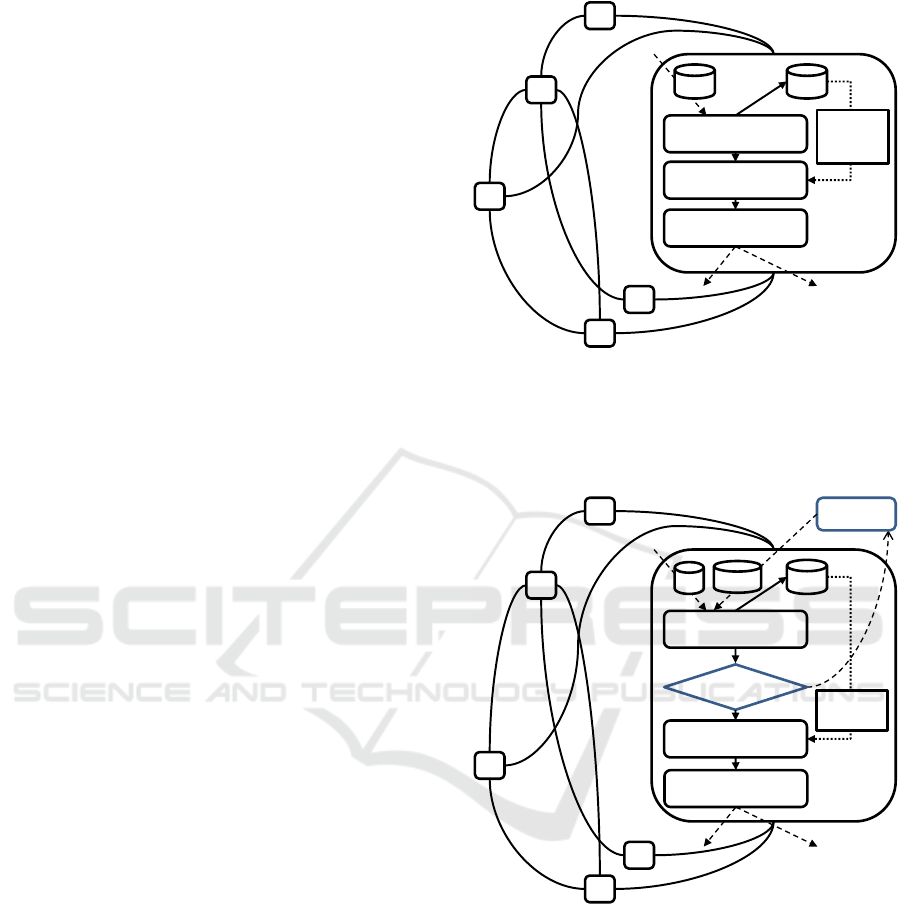
Figure 1: Internal receive-decide-act architecture of an
agent with decision process. The agent receives a set of op-
timum coordinates from another agent, decides on the best
coordinate for the dimensions the agent accounts for and
sends the updated information to all neighbors; cf. (Bremer
and Lehnhoff, 2017a).
perceive:
update knowledge
act:
send workspace














integrate


subset of 1-
dimensinal
solutions
decide:
optimize sub-problem


    
postpone


Figure 2: Extended agent protocol for integrating laziness
into the protocol from Figure 1.
After the update procedure, agent a
j
takes all el-
ements x
k
∈ x
x
x with k 6= j as temporarily fixed and
starts solving a 1-dimensional sub-problem: x
j
=
argmin f (x,x
x
x); where f is the objective function with
all values except element x
j
fixed. This problem with
only x as the single degree of freedom is solved using
Brent’s method (Brent, 1971). Algorithm 1 summa-
rizes this approach.
Brent’s method originally is a root finding pro-
cedure that combines the previously known bisec-
tion method and the secant method with an inverse
quadratic interpolation. Whereas the latter are known
Lazy Agents for Large Scale Global Optimization
75

for fast convergence, bisection provides more relia-
bility. By combining these methods – a first step was
already undertaken by (Dekker, 1969) – convergence
can be guaranteed with at most O(n
2
) iterations (with
n iterations for the bisection method). In case of a
well-behaved function the method converges even su-
perlinearly (Brent, 1971). We used an evaluated im-
plementation from Apache Commons Math after a
reference implementation from (Brent, 1973).
After x
j
has been determined with Brent’s method,
x
j
is communicated (along with all x
`
previously re-
ceived from agent a
i
) to all neighbors if f (x
x
x
∗
) with x
j
gains a better result than the previous solution candi-
date. Figure 1 summarizes this procedure.
Into this agent process, we integrated laziness.
Figure 2 shows the idea. As an additional stage in
the receive-decide-act protocol, a random decision is
made whether to postpone a decision on local opti-
mality based on aggregated information. In contrast
to the approach of (Anders et al., 2012), aggrega-
tion is nevertheless done with this additional stage.
Only after information aggregation and thus after be-
lief update it is randomly decided whether to continue
with the decision process of the current belief (local
optimization of the respective objective dimension)
or with postponing this process. By doing so, addi-
tional information – either update information from
the same agent, or additional information from other
agents – may meanwhile arrive and aggregate. The
delay is realized by putting the trigger message in
a holding stack and resubmitting it later. Figure 3
shows the relative frequencies of delay (additional ag-
gregation steps) that occur when a uniform distribu-
tion U(0, 1) is used for deciding on postponement.
The likelihood of being postponed is denoted by λ. In
this way, information may also take over newer infor-
mation and thus may trigger a resumption at an older
search branch that led to a dead-end. In general, the
disturbance within the system increases, and thus pre-
mature convergence is better prevented. We denote
this extension lazyCOHDAgo.
4 RESULTS
For evaluation, we used a set of well-known test func-
tions that have been developed for benchmarking op-
timization methods: Elliptic, Ackley (Ulmer et al.,
2003), Egg Holder (Jamil and Yang, 2013), Rastri-
gin (Aggarwal and Goswami, 2014), Griewank (Lo-
catelli, 2003), Quadric (Jamil and Yang, 2013), and
examples from the CEC ’13 Workshop on Large Scale
Optimization (Li et al., 2013).
In a first experiment, we tested the effect of lazy
0 10 20 30 40
50
0
0.2
0.4
0.6
delay
rel. frequency
λ = 0.3
λ = 0.6
λ = 0.9
Figure 3: Probability density of postponement delay for dif-
ferent laziness factors λ denoting the probability of post-
poning an agent’s decision process.
agents and solved a set of test functions with agents
of different laziness λ. Table 1 shows the result for
50-dimensional versions of the test functions. In this
rather low dimensional cases the effect is visible, but
not that prominent. In most cases a slight improve-
ment can be seen with growing laziness factor (λ = 0
denotes no laziness at all and thus responds to the
original COHDAgo). The Elliptic function for ex-
ample shows no improvement. In some cases, e. g.
for the Quadric function the result quality deterio-
rates. But, also an overshoot can be observed with
the Griewank function where the best result is ob-
tained with a laziness of λ = 0.3. When applied
to more complex and higher-dimensional objective
functions the effect is way more prominent as can be
seen in Table 2. The CEC f
1
function (Li et al., 2013)
is a shifted elliptic function which is ill-conditioned
with condition number ≈ 10
6
in the 1000-dimensional
case. Due to dimensionality these results have also
been obtained with a laziness of λ = 0.99) From the
wide range of solution qualities for λ = 0.9 – the
achieved minimum result out of 20 runs was (200-
dimensional case) 3.40 × 10
−19
, which is almost as
good as the result for λ = 0.9 – it can be concluded
that the agent system is less susceptible to prema-
ture convergence and thus yields better mean results.
The Rosenbrock function is a asymmetrically, non-
linearly shifted version of (Rosenbrock, 1960) multi-
plied by the Alpine function.
Finally, we compared the results of the lazy agent
approach with other established meta-heuristics for
functions where the agent approach was successful.
Please note that for some function (e. g. . the result in
table 1) were not that promising. For comparison we
used the co-variance matrix adaption evolution strat-
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
76

Table 1: Performance of the lazy agent approach on different 50-dimensional test functions for different laziness factors λ.
function λ = 0.0 λ = 0.3 λ = 0.6 λ = 0.9
Elliptic 1.527 × 10
−21
± 2.876 × 10
−28
1.527 × 10
−21
± 1.976 × 10
−28
1.527 × 10
−1
± 2.594 × 10
−29
1.527 × 10
−21
± 7.48 × 10
−28
Ackley 1.306 × 10
1
± 2.988 × 10
−1
1.217 × 10
1
± 1.665 × 10
−1
1.205 × 10
1
± 1.86 × 10
−1
1.124 × 10
1
± 2.088 × 10
−1
EggHolder 1.453 × 10
4
± 8.639 × 10
2
1.423 × 10
4
± 8.81 × 10
2
1.384 × 10
4
± 9.119 × 10
2
1.345 × 10
4
± 9.441 × 10
2
Rastrigin 2.868 × 10
2
± 2.493 × 10
0
2.87 × 10
2
± 1.569 × 10
0
2.868 × 10
2
± 2.427 × 10
0
2.858 × 10
2
± 3.088 × 10
0
Griewank 2.95 × 10
−3
± 9.328 × 10
−3
1.478 × 10
−3
± 4.674 × 10
−3
1.59 × 10
−3
± 3.219 × 10
−2
3.07 × 10
−2
± 4.132 × 10
−2
Quadric 6.51 × 10
−26
± 6.525 × 10
−26
1.196 × 10
−25
± 8.128 × 10
−26
3.65 × 10
−5
± 5.141 × 10
−25
4.43 × 10
−15
± 1.40 × 10
−14
Table 2: performance of the lazy agent approach on different high-dimensional, ill-conditioned test functions for different
laziness factors λ.
function λ = 0.0 λ = 0.9 λ = 0.99
CEC f
1
, d = 200 1.81 × 10
10
± 5.78 × 10
9
2.20 × 10
8
± 4.11 × 10
8
3.40 × 10
−19
± 1.54 × 10
−23
CEC f
1
, d = 500 4.28 × 10
9
± 8.28 × 10
9
6.55 × 10
4
± 1.85 × 10
5
3.760 × 10
−19
± 1.31 × 10
−21
Rosenbrock
∗
d = 250 1.01 × 10
−5
± 1.71 × 10
−5
2.41 × 10
−7
± 5.37 × 10
−7
5.68 × 10
−8
± 1.60 × 10
−7
Table 3: Comparison of the lazy agent approach with different established meta-heuristics.
f CMA-ES DE PSO lazy COHDAgo
Elliptic 3.41 × 10
−5
± 7.47 × 10
−5
4.48 × 10
−9
± 2.24 × 10
−9
2.65 × 10
5
± 8.37 × 10
5
1.14 × 10
−21
± 2.64 × 10
−27
Ackley 1.02 × 10
1
± 7.07 × 10
0
4.73 × 10
−2
± 7.06 × 10
−5
2.0 × 10
1
± 0.0 × 10
0
1.54 × 10
1
± 1.01 × 10
−1
Alpine 4.2 × 10
0
± 3.96 × 10
0
2.82 × 10
−3
± 9.18 × 10
−5
6.61 × 10
−9
± 1.29 × 10
−8
4.51 × 10
−12
± 1.32 × 10
−13
Griewank 9.99 × 10
−4
± 3.11 × 10
−3
4.41 × 10
−4
± 1.51 × 10
−5
8.92 × 10
−3
± 4.54 × 10
−3
5.11 × 10
−16
± 9.2 × 10
−16
Table 4: Respective best results (residual error) out of 20 runs each for the comparison from Table 3.
f CMA-ES DE PSO lazy COHDAgo
Elliptic 9.28 × 10
−7
1.89 × 10
−9
1.04 × 10
−4
1.14 × 10
−21
Ackley 6.02 × 10
−6
4.73 × 10
−2
2.0 × 10
1
1.52 × 10
1
Alpine 1.28 × 10
−1
2.7 × 10
−3
1.2 × 10
−15
4.3 × 10
−12
Griewank 3.57 × 10
−6
4.23 × 10
−4
1.51 × 10
−5
0.0 × 10
0
egy (CMA-ES) from (Hansen and Ostermeier, 2001)
with a parametrization after (Hansen, 2011), Differ-
ential Evolution (Storn and Price, 1997) and Particle
Swarm Optimization (Kennedy and Eberhart, 1995).
The lazy COHDAgo approach has been parametrized
with a laziness of λ = 0.9. Table 3 shows the result.
As the agent approach terminates by itself if no
further solution improvement can be made by any
agent and no further stopping criterion is meaningful
in an asynchronously working decentralized system,
we simply logged the number of used function eval-
uations and gave this number as evaluation budget to
the other heuristics. In this way we ensured that every
heuristics uses the same budget of maximum objec-
tive evaluations. As CMA-ES was not able to succeed
for some high-dimensional functions with this limited
budget, this evolution strategy was given the 100 fold
budget.
The agent approach is competitive for the Ackley
function. In most of the cases lazyCOHDAgo suc-
ceeds in terms of residual error, but also, when look-
ing at the absolute best solution out of 20 run each
(Table 4), the lazy agent-approach is successful.
5 CONCLUSION
Large scale global optimization is a crucial task for
many real world applications in industry and en-
gineering. Most meta-heuristics deteriorate rapidly
with growing problem dimensionality. We proposed
a laziness extension to an agent-based algorithm for
global optimization and achieved a way better perfor-
mance when applied to large scale problems. By ran-
domly postponing the agent’s decision on local opti-
mization leads to less vulnerability to premature con-
vergence, obviously due to an increasing inter-agent
variation (Anders et al., 2012) and thus to the incor-
poration of past (outdated) information. This may re-
stimulate search in already abandoned paths. Delay-
ing the reaction of the agents in COHDA is known to
increase the diversity in the population and thus lead-
ing to at least equally good results but with a larger
number of steps (Hinrichs and Sonnenschein, 2014),
but for some use cases – like large scale global opti-
mization also to better results.
The lazy COHDAgo approach has shown good
and sometimes superior performance especially re-
Lazy Agents for Large Scale Global Optimization
77

garding solution quality. In future work, it may also
be promising to further scrutinize the impact of the
communication topology as design parameter.
REFERENCES
Aggarwal, S. and Goswami, P. (2014). Implementation of
dejong function by various selection method and ana-
lyze their performance. IJRCCT, 3(6).
Ahrari, A. and Shariat-Panahi, M. (2015). An improved
evolution strategy with adaptive population size. Op-
timization, 64(12):2567–2586.
Anders, G., Hinrichs, C., Siefert, F., Behrmann, P., Reif,
W., and Sonnenschein, M. (2012). On the Influence
of Inter-Agent Variation on Multi-Agent Algorithms
Solving a Dynamic Task Allocation Problem under
Uncertainty. In Sixth IEEE International Conference
on Self-Adaptive and Self-Organizing Systems (SASO
2012), pages 29–38, Lyon, France. IEEE Computer
Society. (Best Paper Award).
B
¨
ack, T., Fogel, D. B., and Michalewicz, Z., editors (1997).
Handbook of Evolutionary Computation. IOP Pub-
lishing Ltd., Bristol, UK, UK, 1st edition.
Bremer, J. and Lehnhoff, S. (2016). A decentralized
PSO with decoder for scheduling distributed electric-
ity generation. In Squillero, G. and Burelli, P., editors,
Applications of Evolutionary Computation: 19th Eu-
ropean Conference EvoApplications (1), volume 9597
of Lecture Notes in Computer Science, pages 427–
442, Porto, Portugal. Springer.
Bremer, J. and Lehnhoff, S. (2017a). An agent-based ap-
proach to decentralized global optimization: Adapt-
ing cohda to coordinate descent. In van den Herik,
J., Rocha, A., and Filipe, J., editors, ICAART 2017
- Proceedings of the 9th International Conference on
Agents and Artificial Intelligence, volume 1, pages
129–136, Porto, Portugal. SciTePress, Science and
Technology Publications, Lda.
Bremer, J. and Lehnhoff, S. (2017b). Decentralized coali-
tion formation with agent-based combinatorial heuris-
tics. ADCAIJ: Advances in Distributed Computing
and Artificial Intelligence Journal, 6(3).
Bremer, J. and Lehnhoff, S. (2017c). Hybrid Multi-
ensemble Scheduling, pages 342–358. Springer Inter-
national Publishing, Cham.
Bremer, J. and Sonnenschein, M. (2014). Parallel tempering
for constrained many criteria optimization in dynamic
virtual power plants. In Computational Intelligence
Applications in Smart Grid (CIASG), 2014 IEEE Sym-
posium on, pages 1–8.
Brent, R. (1973). Algorithms for Minimization Without
Derivatives. Dover Books on Mathematics. Dover
Publications.
Brent, R. P. (1971). An algorithm with guaranteed conver-
gence for finding a zero of a function. Comput. J.,
14(4):422–425.
Colorni, A., Dorigo, M., Maniezzo, V., et al. (1991). Dis-
tributed optimization by ant colonies. In Proceedings
of the first European conference on artificial life, vol-
ume 142, pages 134–142. Paris, France.
Dekker, T. (1969). Finding a zero by means of successive
linear interpolation. Constructive aspects of the fun-
damental theorem of algebra, pages 37–51.
Dorigo, M. and St
¨
utzle, T. (2004). Ant Colony Optimiza-
tion. Bradford Company, Scituate, MA, USA.
Gano, S. E., Kim, H., and Brown II, D. E. (2006). Compar-
ison of three surrogate modeling techniques: Datas-
cape, kriging, and second order regression. In Pro-
ceedings of the 11th AIAA/ISSMO Multidisciplinary
Analysis and Optimization Conference, AIAA-2006-
7048, Portsmouth, Virginia.
Hansen, E. (1980). Global optimization using interval anal-
ysis – the multi-dimensional case. Numer. Math.,
34(3):247–270.
Hansen, N. (2006). The CMA evolution strategy: a compar-
ing review. In Lozano, J., Larranaga, P., Inza, I., and
Bengoetxea, E., editors, Towards a new evolutionary
computation. Advances on estimation of distribution
algorithms, pages 75–102. Springer.
Hansen, N. (2011). The CMA Evolution Strategy: A Tuto-
rial. Technical report.
Hansen, N. and Ostermeier, A. (2001). Completely deran-
domized self-adaptation in evolution strategies. Evol.
Comput., 9(2):159–195.
Hansen, P., Jaumard, B., and Lu, S.-H. (1992). Global op-
timization of univariate lipschitz functions ii: New al-
gorithms and computational comparison. Math. Pro-
gram., 55(3):273–292.
Hinrichs, C. and Sonnenschein, M. (2014). The Effects
of Variation on Solving a Combinatorial Optimiza-
tion Problem in Collaborative Multi-Agent Systems.
In Mller, J. P., Weyrich, M., and Bazzan, A. L., edi-
tors, Multiagent System Technologies, volume 8732 of
Lecture Notes in Computer Science, pages 170–187.
Springer International Publishing.
Hinrichs, C., Sonnenschein, M., and Lehnhoff, S. (2013).
Evaluation of a Self-Organizing Heuristic for Inter-
dependent Distributed Search Spaces. In Filipe, J.
and Fred, A. L. N., editors, International Conference
on Agents and Artificial Intelligence (ICAART 2013),
volume Volume 1 – Agents, pages 25–34. SciTePress.
Hinrichs, C., Vogel, U., and Sonnenschein, M. (2011). Ap-
proaching decentralized demand side management via
self-organizing agents. Workshop.
Horst, R. and Pardalos, P. M., editors (1995). Handbook of
Global Optimization. Kluwer Academic Publishers,
Dordrecht, Netherlands.
Jamil, M. and Yang, X. (2013). A literature survey of
benchmark functions for global optimization prob-
lems. CoRR, abs/1308.4008.
Kennedy, J. and Eberhart, R. (1995). Particle swarm op-
timization. In Neural Networks, 1995. Proceedings.,
IEEE International Conference on, volume 4, pages
1942–1948 vol.4. IEEE.
Kramer, O. (2010). A review of constraint-handling tech-
niques for evolution strategies. Appl. Comp. Intell.
Soft Comput., 2010:1–19.
ICAART 2019 - 11th International Conference on Agents and Artificial Intelligence
78

Leung, Y., Gao, Y., and Xu, Z.-B. (1997). Degree of pop-
ulation diversity - a perspective on premature con-
vergence in genetic algorithms and its markov chain
analysis. IEEE Transactions on Neural Networks,
8(5):1165–1176.
Li, X., Tang, K., Omidvar, M. N., Yang, Z., and Qin, K.
(2013). Benchmark functions for the cec2013 spe-
cial session and competition on large-scale global op-
timization. techical report.
Li, Y., Mascagni, M., and Gorin, A. (2009). A decentralized
parallel implementation for parallel tempering algo-
rithm. Parallel Computing, 35(5):269–283.
Locatelli, M. (2003). A note on the griewank test function.
Journal of Global Optimization, 25(2):169–174.
Loshchilov, I., Schoenauer, M., and Sebag, M. (2012). Self-
adaptive surrogate-assisted covariance matrix adapta-
tion evolution strategy. CoRR, abs/1204.2356.
Nieße, A. (2015). Verteilte kontinuierliche Einsatzplanung
in Dynamischen Virtuellen Kraftwerken. PhD thesis.
Nieße, A., Beer, S., Bremer, J., Hinrichs, C., L
¨
unsdorf, O.,
and Sonnenschein, M. (2014). Conjoint Dynamic Ag-
gregation and Scheduling Methods for Dynamic Vir-
tual Power Plants. In Ganzha, M., Maciaszek, L. A.,
and Paprzycki, M., editors, Proceedings of the 2014
Federated Conference on Computer Science and In-
formation Systems, volume 2 of Annals of Computer
Science and Information Systems, pages 1505–1514.
IEEE.
Nieße, A., Bremer, J., Hinrichs, C., and Sonnenschein, M.
(2016). Local Soft Constraints in Distributed En-
ergy Scheduling. In Proceedings of the 2016 Feder-
ated Conference on Computer Science and Informa-
tion Systems (FEDCSIS), pages 1517–1525. IEEE.
Ortega, J. M. and Rheinboldt, W. C. (1970). Iterative solu-
tion of nonlinear equations in several variables.
Rahnamayan, S., Tizhoosh, H. R., and Salama, M. M.
(2007). A novel population initialization method for
accelerating evolutionary algorithms. Computers &
Mathematics with Applications, 53(10):1605 – 1614.
Rechenberg, I. (1965). Cybernetic solution path of an exper-
imental problem. Technical report, Royal Air Force
Establishment.
Rigling, B. D. and Moore, F. W. (1999). Exploitation of
sub-populations in evolution strategies for improved
numerical optimization. Ann Arbor, 1001:48105.
Rosenbrock, H. H. (1960). An Automatic Method for Find-
ing the Greatest or Least Value of a Function. The
Computer Journal, 3(3):175–184.
Rudolph, G. (2001). Self-adaptive mutations may lead to
premature convergence. IEEE Transactions on Evolu-
tionary Computation, 5(4):410–414.
Shang, Y.-W. and Qiu, Y.-H. (2006). A note on the extended
rosenbrock function. Evol. Comput., 14(1):119–126.
Simon, D. (2013). Evolutionary Optimization Algorithms.
Wiley.
Sobieszczanski-Sobieski, J. and Haftka, R. T. (1997). Mul-
tidisciplinary aerospace design optimization: survey
of recent developments. Structural optimization,
14(1):1–23.
Sonnenschein, M., L
¨
unsdorf, O., Bremer, J., and Tr
¨
oschel,
M. (2014). Decentralized control of units in smart
grids for the support of renewable energy supply. En-
vironmental Impact Assessment Review, (0):–. in
press.
Storn, R. and Price, K. (1997). Differential evolution – a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of Global Optimiza-
tion, 11(4):341–359.
Talbi, E. (2009). Metaheuristics: From Design to Imple-
mentation. Wiley Series on Parallel and Distributed
Computing. Wiley.
Trelea, I. C. (2003). The particle swarm optimization algo-
rithm: convergence analysis and parameter selection.
Information Processing Letters, 85(6):317 – 325.
Tuy, H., Thieu, T., and Thai, N. (1985). A conical algo-
rithm for globally minimizing a concave function over
a closed convex set. Math. Oper. Res., 10(3):498–514.
Ulmer, H., Streichert, F., and Zell, A. (2003). Evolu-
tion strategies assisted by gaussian processes with im-
proved pre-selection criterion. In in IEEE Congress
on Evolutionary Computation,CEC 2003, pages 692–
699.
Vanneschi, L., Codecasa, D., and Mauri, G. (2011). A
comparative study of four parallel and distributed pso
methods. New Generation Computing, 29(2):129–
161.
Watts, D. and Strogatz, S. (1998). Collective dynamics of
’small-world’ networks. Nature, (393):440–442.
Weise, T., Chiong, R., and Tang, K. (2012). Evolution-
ary optimization: Pitfalls and booby traps. Journal
of Computer Science and Technology, 27(5):907–936.
Wright, S. J. (2015). Coordinate descent algorithms. Math-
ematical Programming, 151(1):3–34.
Lazy Agents for Large Scale Global Optimization
79