Feature Extraction of Epileptic EEG in Spectral Domain via Functional

Data Analysis

Shengkun Xie

and Anna Lawniczak

Ted Rogers School of Management, Ryerson University, Toronto, Canada

Department of Mathematics and Statistics, University of Guelph, Guelph, Canada

Keywords:

Functional Data Analysis, Power Spectrum, Functional Principal Component Analysis, EEG, Epilepsy

Diagnosis.

Abstract:

Functional data analysis is a natural tool for functional data to discover functional patterns. It is also often

used to investigate the functional variation of random signals. In this work, we propose a novel approach by

analyzing EEG signals in the spectral domain using functional data analysis techniques including functional

descriptive statistics, functional probes, and functional principal component analysis. By ﬁrst transforming

EEG signals into their power spectra, the functionality of random signals is greatly enhanced. Because of this

improvement, the application of functional data analysis becomes meaningful in feature extraction of random

signals. Our study also illustrates a great potential of using functional PCA as a feature extractor for EEG

signals in epilepsy diagnosis.

1 INTRODUCTION

Feature extraction of high dimensional data has been

an important research area in machine learning (Bou-

veyron et al., 2007; Kriegel et al., 2009; Yu and Liu,

2003; Jimenez and Landgrebe, 1998). It aims at ob-

taining a set of key features, so that, the complexity

of data classiﬁcation can be greatly reduced. Ideally,

in feature extraction, one looks for a highly separable

feature vector as an input for the classiﬁcation prob-

lem. However, the degree of inseparability signiﬁ-

cantly affects the choice of a classiﬁcation method.

If the extracted features are either linearly or non-

linearly separable, there is no extra effort needed to

select a suitable classiﬁcation method. In biomedi-

cal signal classiﬁcation (such as EEG or ECG classi-

ﬁcation), due to its high dimensional nature, feature

extraction of the given signals is often the most im-

portant step to meet the success of classiﬁcation (Al-

ickovic et al., 2018; Truong et al., 2017; Fergus et al.,

2016). After the feature vector is obtained, a classi-

ﬁcation method such as linear discriminate analysis

(LDA), k-nearest neighbor (KNN), or support vector

machines (SVM) is then applied to determine a group

membership.

In many real-world applications of biomedical

signal classiﬁcation (Qazi et al., 2016; Li et al., 2005;

Phinyomark et al., 2012; Gandhi et al., 2011; Subasi

and Gursoy, 2010), a low dimensional and linear or

non-linearly separable feature vector is highly desir-

able for both, the ease of data visualization in med-

ical devices and a possibility of using a simple clas-

siﬁcation method, such as a linear classiﬁer or the k-

nearest neighbor method. To meet this goal, there is a

lot of current research focusing on feature extraction

of signals in the time domain using sparse represen-

tation of signals (Zhang et al., 2015). This type of

research aims at extracting a low dimensional feature

vector through sparse decomposition of signals and

improvement of the linear or non-linear separability

by selecting its most discriminative features. Often

the ﬁrst goal is easy to achieve by enforcing the spar-

sity on signal approximation, but it is more difﬁcult to

make a set of good features, which are linearly or non-

linearly separable. Among many published research

works, the time-frequency decomposition technique

is the most popular within this type. It decomposes

the signal in terms of time and frequency domain

components. By doing time-frequency domain de-

composition, the separability of signals is greatly im-

proved. The classiﬁcation is then based on extracted

features in time and frequency domains, which are the

coefﬁcients of the selected time-frequency basis func-

tions (Nyan et al., 2006; Garcia et al., 2003).

Functional data analysis (FDA) is a natural tool

for studying functional data, such as images, temper-

118

Xie, S. and Lawniczak, A.

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis.

DOI: 10.5220/0007353301180127

In Proceedings of the 8th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2019), pages 118-127

ISBN: 978-989-758-351-3

ature data, or growth curves (Ramsay, 2005; Wang

et al., 2016; Ramsay and Silverman, 2007). This is

due to the existence of stable, and highly observable

deterministic patterns contained in the data, as a part

of the key signal features. When data is functional

in nature and discriminative, a set of coefﬁcients of

basis functions can be obtained by signal representa-

tion using common basis functions. From statistical

point of view, this belongs to a functional regression

problem, and it is usually addressed by an ordinary

least square method or a regularization based least

square method. The classiﬁcation of signals can be

done by classifying the extracted coefﬁcients obtained

from signal representation using basis functions. On

the other hand, FDA allows us to investigate the func-

tional variation at various levels. This creates another

layer of feature extraction by further looking at the de-

composition of data variation. When random signals

are not functional in nature, the application of FDA

may not be successful. In theory, a random signal can

be represented in terms of a linear combination of in-

ﬁnite basis functions. This essentially allows applica-

bility of using FDA for random signals. However, for

decomposition of random signals, the coefﬁcients of

basis functions, from signal to signal, are often highly

volatile, due to the fact that the signals are lacking

functional nature. The classiﬁcation of extracted fea-

tures may be difﬁcult due to high variability, high di-

mensionality and lack of separability of the features.

This may call for a novel approach in order to improve

the functionality of random signals in a given domain.

In this work, we propose a novel approach and

illustrate it by analyzing EEG signals in the spec-

tral domain using functional data analysis techniques

including functional descriptive statistics, functional

probes and functional principal component analysis.

We ﬁrst transform EEG signals into power spectra to

improve the functionality of EEG signals. We then

use functional PCA to extract signal features. We also

demonstrate the application of the proposed method

for epilepsy diagnosis (Lima et al., 2009; Liang et al.,

2010). The signiﬁcance of this work is the novelty of

the proposed method and the achieved high separabil-

ity of the considered data, as well as the high applica-

bility of the method to other types of signals such as

ﬁnancial time series and long-term observational eco-

nomical data for classiﬁcation or pattern recognition

problems. Unlike the regular use of functional princi-

pal component analysis, which aims at either estimat-

ing the functionality or capturing functional data vari-

ation, our work emphasizes the feature extraction of

signals. This paper is organized as follows. In Section

2, we discuss the proposed methods including spectral

analysis and functional data analysis. In Section 3,

the analysis of publicly available EEG data and sum-

mary of main results are presented. Finally, we con-

clude our ﬁndings and provide further remarks in Sec-

tion 4.

2 METHODS

Statistical measures, models or distributions are often

used for pattern recognition of high dimensional data

or signals. Most of the real-life signals are stochas-

tic and the pattern of how they are related is mea-

sured by sample auto-covariance matrix or sample

auto-correlation matrix in the time domain. The auto-

covariance matrix is then further decomposed using

various matrix decomposition methods to reduce the

dimension of feature space. For epileptic EEG sig-

nals, our study shows that there is a better functional

relationship between the periodograms and the fre-

quency values than the pattern in the time domain.

This motivates us to study functional data analysis in

a spectral domain for clustering EEG signals, instead

of analyzing signals in the original time domain. We

will ﬁrst discuss the transformation of a signal to the

spectral domain.

2.1 Spectral Analysis

For a given signal X

of length n, sampled at discrete

times, we deﬁne the discrete Fourier transform (DFT)

to be

d(ω

) = n

−1/2

∑

t=1

−2πiω

(1)

for j = 0, 1,..., n − 1, where the frequency ω

= j/n.

Transforming the signal by discrete Fourier transform

allows to obtain a concentration of signal powers us-

ing a small set of more dominant frequencies. This

means that one is able to focus on a selected ω

and

its transformed values d(ω

) only.

By applying the inverse DFT to d(ω

), the signal

can be exactly recovered as follows:

= n

−1/2

n−1

∑

j=0

d(ω

2πiω

. (2)

The periodogram for each frequency ω

is deﬁned as

I(ω

) = | d(ω

) |

∑

t=1

∑

s=1

−

X)(X

−

X)e

−2πiω

(t−s)

n−1

∑

h=−(n−1)

n−|h|

∑

t=1

t+|h|

−

X)(X

−

X)e

−2πiω

n−1

∑

h=−(n−1)

γ(h)e

−2πiω

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis

119

where

γ(h) is the auto-covariance function of time lag

h. In the above, we used the fact that

∑

t=1

−2πiω

= 0. (3)

Notice that the periodogram is just the Fourier trans-

form of the auto-covariance function, which captures

the quadratic covariation of signal in the spectral do-

main.

Furthermore, we can express the periodogram as a

sum of squared sine and cosine transforms of a signal

as follows:

| d(ω

) |

= d

(ω

) + d

(ω

) (4)

where d

(ω

) is the cosine transform and d

(ω

) is

the sine transform of the signal. These transforms are

deﬁned, respectively, as follows:

(ω

) = n

−1/2

∑

t=1

cos(2πω

t) (5)

(ω

) = n

−1/2

∑

t=1

sin(2πω

t), (6)

where j = 0,1, 2, ...,n − 1. I(ω

) is also called a

power spectrum of a signal X

. Because of its deﬁni-

tion, a periodogram captures the distribution of vari-

ation of a signal in the spectral domain. The larger

a value of the periodogram the more dominant is its

corresponding frequency. Thus, the dominant val-

ues determine the signal power spectra. Often these

more dominant frequencies correspond to smaller fre-

quency values, which implies that local patterns are

more signiﬁcant than the global one, after the signal

is transformed into the spectral domain. Because of

this, we only focus on the analysis of the power spec-

trum in a sub-interval, i.e. we analyze only the ﬁrst

200 frequency values for the given signals.

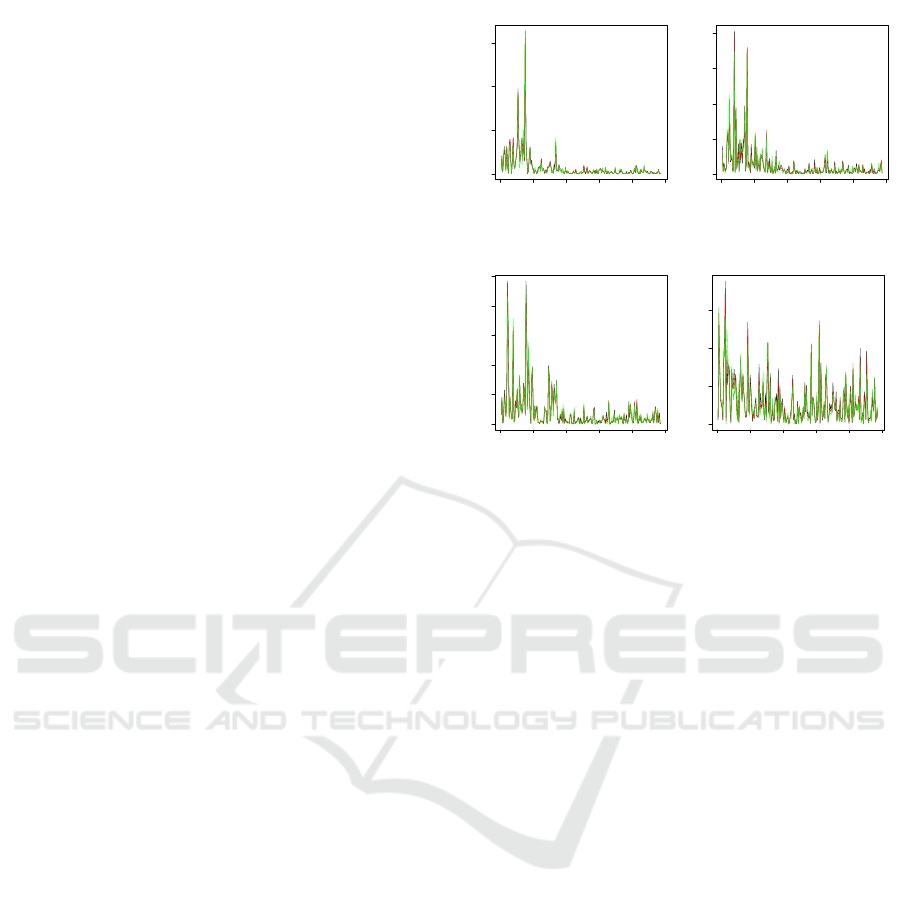
To illustrate the above points, we present a set

of results of the power spectra for selected different

types of EEG signals in Figure 1 (the data set will be

discussed later). One can clearly see that the power

spectra of the ﬁrst 200 frequency values behave sim-

ilarly within each set of data, but their patterns look

differently over different frequency values.

2.2 Functional Data Analysis

Often a signal is sampled at discrete times. However,

functional data analysis allows us to model the power

spectrum of a signal with discrete observations by a

linear combination of a set of continuous basis func-

tions. Mathematically, for the ith signal in a given

data set, we can expand the power spectrum I

(ω) by

(ω) =

∑

k=1

(ω), (7)

0.00 0.01 0.02 0.03 0.04 0.05

0 50000 100000 150000

Frequency

Signal Power

(a) Set A

0.00 0.01 0.02 0.03 0.04 0.05

0 50000 100000 150000 200000

Frequency

Signal Power

(b) Set B

0.00 0.01 0.02 0.03 0.04 0.05

0e+00 2e+04 4e+04 6e+04 8e+04 1e+05

Frequency

Signal Power

0.00 0.01 0.02 0.03 0.04 0.05

0 20000 40000 60000

Frequency

Signal Power

(d) Set D

Figure 1: Sample plots of the power spectra for data sets A

(Normal: Eyes Closed), B (Normal: Eyes Open), C (Non-

epileptogenic zone) and D (Epileptogenic zone), respec-

tively. Each plot contains three sample power spectra of

the ﬁrst 200 frequency values.

where ω is the frequency value, α

is the coefﬁcient

of the kth basis function and K is the total number of

basis functions. In feature extraction, since our objec-

tive is not to fully represent a power spectrum using

a set of functional basis, often a small ﬁnite number

K is chosen. That is, we approximate the power spec-

trum by a linear combination of a small number of

K basis functions. Notice that, within the discussion

of this section, we do not separate the mean function

from the representation of a signal, but in the later dis-

cussion we will separate the mean function from the

signal expansion because we will study the functional

variation of the signal power spectra.

For a sample of N signals, the matrix notation of

power spectrum becomes

I(ω) = CΦ(ω) (8)

where I(ω) is a column vector of length N, Φ(ω) is a

column vector of length K containing the basis func-

tions, and C is the coefﬁcient matrix of size N × K.

Notice that the basis function φ(ω) can be different

for various groups of signals. However, because we

will consider the signals which share many common-

alities in the spectral domain, it is more reasonable

to use the same basis functions for all the considered

groups of signals. This will allow us to extract sig-

nal features within the same feature space. In func-

tional data analysis, there are two types of basis func-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

120

tions: periodical basis functions and non-periodical

basis functions. In this work, we select non-periodical

basis functions as we don’t expect that power spectra

to be periodic. Within non-periodical basis functions,

B-spline basis function is the most popular one, there-

fore we choose this type of basis function for our in-

vestigation (De Boor et al., 1978; Unser et al., 1993).

Of course, we cannot rule out the possibility of the ef-

fect of selected basis functions, so we will investigate

this effect in this work.

2.2.1 Functional Descriptive Statistics

Summary statistics are often the key features, which

are useful for signal classiﬁcation. Since we have

the functional representation of data, the basic sum-

mary statistics can be expressed in functional form as

a function of frequency ω.

For a given set of sample of length N, the func-

tional mean power spectrum is given as follows:

I(ω) = N

−1

∑

i=1

(ω) = N

−1

∑

i=1

∑

k=1

(ω)

∑

k=1

(ω), (9)

where

is the average of the coefﬁcients at a given

frequency of the N signals. When N → ∞,

→ α

where α

is the true coefﬁcient of φ

(ω). In this case,

we can denote the mean power spectrum by

µ(ω) =

∑

k=1

(ω). (10)

Similarly to the sample variance, the functional vari-

ance, calculated based on N sample power spectra, is

given by

i(ω)

N − 1

∑

i=1



(ω) −

I(ω)



N − 1

∑

i=1



∑

k=1

(ω) −

∑

k=1

(ω)



N − 1

∑

i=1



∑

k=1

(α

−

)φ

(ω)



. (11)

For a given sample of N signals, the functional

variance-covariance at two different frequency values

and ω

can be estimated by

v(ω

,ω

) =

N − 1

∑

i=1



(ω

) −

I(ω

)





(ω

) −

I(ω

)



. (12)

2.2.2 Functional Probes

Purely descriptive statistics such as functional mean,

functional variance, or functional covariance, allow

us to see the functional central tendency and the func-

tional variation pattern of signal power spectra. How-

ever, they are high dimensional statistics. In signal

classiﬁcation, the dimensions of these functional de-

scriptive statistics must be further reduced. Here, we

consider an application of functional probes. A probe

is a measure allowing us to see speciﬁc variation

by deﬁning a functional weight ξ(ω), and it is deﬁned

ξ(ω)I(ω)dω. (13)

This is an inner product of functions ξ(ω) and I(ω).

The ξ(ω) has been structured so that we can extract

speciﬁc features or patterns of the variation in power

spectrum I(ω). In this work, we choose functional

mean and functional standard deviation of the power

spectrum from a given group of signals as weight

functions. The probe values for the ith signal power

spectrum using functional mean and functional stan-

dard deviation of the jth group power spectrum be-

comes

i j

( j )

(ω)I

(ω)dω

∑

( j )

(ω)φ

(ω)dω,

i j

( j )

i(ω)

(ω)dω. (14)

The functional probe values capture the similarity

between the weight function and the ith power spec-

trum of a signal. When the basis functions are or-

thonormal ( i.e.,

(ω)φ

(ω)dω = 0, for k

6= k

and

(ω)dω = 1, for k = 1,2,..., K), the probe

value using a functional mean becomes

i j

∑

k=1

( j )

, (15)

which can be interpreted as a similarity measure be-

tween two different groups of signals in the spectral

domain. However, the closed form does not exist for

probe value using functional standard deviation.

So far, we have discussed functional probe values

based on the power spectrum I(ω). If we replace I(ω)

by v(ω

,ω

), i.e. the variance-covariance function,

the functional probe value becomes

ξ(ω

)v(ω

,ω

)dω

. (16)

This is exactly the left hand side of the eigen-equation

for solving eigenvalues and eigenvectors in func-

tional principal component analysis, which will be

discussed in the next section.

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis

121

2.2.3 Functional Principal Component Analysis

In multivariate statistics, principal component anal-

ysis (PCA) of p-variate random vector X =

,... ,X

) looks for a set of weight values,

=(ξ

1 j

,ξ

2 j

,... ,ξ

p j

), so that, at the jth step, the lin-

ear combination of variables X

has the greatest vari-

ance. That is Var(

∑

i=1

i j

), or in the matrix nota-

tion, Var(ξ

X) is maximized. For j = 1,2,. . ., p, this

process is repeated by replacing each X

by the value

obtained after subtracting the previous principal com-

ponent, subject to

∑

i=1

i j

= 1 and

∑

i=1

i j

= 0 for

j < l, and 1 ≤ l, j ≤ p. The actual implementation of

this procedure can be done by a singular value decom-

position (SVD) of the data matrix X, which contains

N realizations of X. In this work, data matrix X be-

comes I(ω), which is also an N × p data matrix, where

p is the total number of frequency values being con-

sidered. Formally, the SVD of I(ω) is a factorization

of the form UΣV, where U is a N × N unitary matrix,

Σ is a N × p matrix consisting of eigenvalues of I(ω),

and V is a p× p unitary matrix. The columns of U and

the columns of V are called the left eigenvector and

the right eigenvector of I(ω), respectively. Also, each

column of V is just the weight vector ξ

. The feature

extraction of data matrix I(ω) becomes the computa-

tion of I(ω)ξ

, for j = 1,2,. .., p. For example, the

ﬁrst principal component scores set is I(ω)ξ

, and the

second principal component scores set is I(ω)ξ

Notice that, the functional probes discussed above

aim at capturing the variation of data associated with

the weight function. If we carefully select the func-

tional weight ξ(ω), so that the variance of func-

tional probe values in (13) is maximized, subject

to the constraint that

(ω)ξ

(ω)dω = 0 for l 6=

j, and

(ω)dω = 1, then this becomes the func-

tional PCA. In this case, functional probe values are

the principal component scores and the weight func-

tion becomes functional principal component loading.

From the discussion above, we can see the connection

between the multivariate PCA and functional PCA. If

we focus on only the discrete values of ω, then func-

tional PCA becomes multivariate PCA. However, the

functional PCA allows us to explore the functional

variation of different principal components.

Suppose that the power spectrum of a given signal

can be expanded using K basis functions, which is

given as follows:

(ω) = µ(ω) +

∑

k=1

(ω), (17)

where µ(ω) is the functional mean of power spectrum.

We may then express this in a matrix notation

I − µ = Cφ, (18)

where C is the N × K coefﬁcient matrix, and

φ=(φ

,φ

,... ,φ

)

. Now, we consider how to obtain

the function principal components and their scores.

First let us denote the variance-covariance function by

v(ω

,ω

). This function is deﬁned in (12). In matrix

form the variance-covariance function is

v(ω

,ω

) =

N − 1

(ω

Cφ(ω

). (19)

Next, to ﬁnd the principal component weight func-

tions, we have to solve the following eigen-equation

for the appropriate eigenvalue λ

v(ω

,ω

)ξ(ω

)dω

= λξ(ω

). (20)

Suppose that the eigen-function ξ(ω) has an expan-

sion

ξ(ω) =

∑

k=1

(ω), (21)

or in the matrix notation

ξ(ω) = φ

(ω)b, (22)

where b=(b

,... ,b

). This yields

v(ω

,ω

)ξ(ω

)dω

N − 1

(ω

φ(ω

)φ

(ω

)bdω

N − 1

(ω

CΦb,

where Φ=

φ(ω)φ

(ω)dω is a K × K matrix. Thus,

the eigen-equation (20) becomes

N − 1

(ω)C

CΦb = λφ

(ω)b. (23)

Since equation (23) must hold for all ω, this implies

the following matrix equation

N − 1

CΦb = λb. (24)

To obtain the required principal components, we de-

ﬁne u = Φ

1/2

b, thus the equation (24) becomes

N − 1

1/2

CΦ

1/2

u = λu. (25)

By solving the symmetric eigenvalue problem in (25)

for u, and then computing b = Φ

−1/2

u one gets the

eigen-function ξ(ω), which is given by

ξ(ω) = φ

(ω)Φ

−1/2

u. (26)

If φ

(ω) are orthogonal, then Φ becomes the K ×

K identity matrix. Thus, the eigen-analysis of the

functional PCA problem in (24) reduces to

N − 1

Cb = λb, (27)

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

122

which is the multivariate PCA that replaces variance-

covariance matrix by the coefﬁcient matrix C ob-

tained from the function approximation of power

spectrum. From the discussion above, we notice that

the multivariate PCA conducts eigen-analysis for a

p × p covariance matix. With the function approxi-

mation using K basis functions, the eigen-analysis of

functional PCA is applied to a K × K coefﬁcient ma-

trix, which depends on the value of K. In the case

of using sparse approximation, which gives a small

value of K, the problem is more efﬁcient in terms of

computational complexity.

0.00 0.01 0.02 0.03 0.04 0.05

0 5000 10000 15000 20000 25000 30000 35000

Frequency

Signal Power

(a) Set A

0.00 0.01 0.02 0.03 0.04 0.05

0 10000 20000 30000 40000 50000

Frequency

Signal Power

(b) Set B

0.00 0.01 0.02 0.03 0.04 0.05

0 5000 10000 15000 20000 25000 30000

Frequency

Signal Power

0.00 0.01 0.02 0.03 0.04 0.05

0 5000 10000 15000 20000 25000 30000 35000

Frequency

Signal Power

(d) Set D

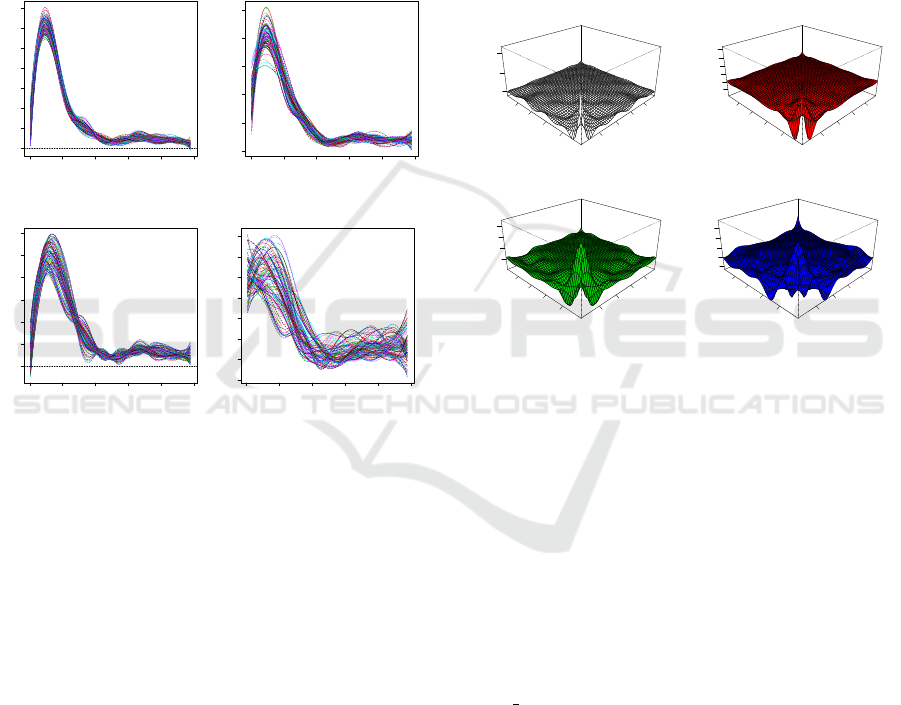
Figure 2: The plots of functional power spectrum for data

sets A (Normal: Eyes Closed), B (Normal: Eyes Open),

C (Non-epileptogenic zone) and D (Epileptogenic zone) re-

spectively. 10 B-splines basis functions are used to smooth

sample power spectra.

2.2.4 Feature Extraction by Functional

Principal Component Analysis

After the eigen-function ξ(ω) is obtained, we can ex-

tract the principal component scores, denoted by P

for the given power spectrum I(ω) by the following

formula

I(ω)ξ

(ω)dω, j = 1,.. .,K. (28)

Subsitituting (18) and (26) into the equation

above, we get

(µ(ω) + Cφ(ω))φ

(ω)Φ

−1/2

dω. (29)

µφ

−1/2

Cφφ

−1/2

= ¯µΦ

−1/2

+ CΦ

−1/2

, (30)

where ¯µ =

µ(ω)φ

(ω)dω. Thus, P

to the ﬁrst prin-

cipal component score vector of the N signal power

spectra, and P

is the second principal component

score vector, and so on.

Notice that, to fully represent a given power

spetrum I

(ω), the number of basis functions K may

approach to inﬁnity. However, for the purpose of fea-

ture extraction, we aim for a low dimensional fea-

ture subspace, which may require a choice of small

K value. We then use a cubic B-spline basis, which

gives the order number to be 4, and we select the num-

ber of basis functions K to be 10. This selection leads

to a good approximation of the power spectra.

Frequency

0.01

0.02

0.03

0.04

Frequency

0.01

0.02

0.03

0.04

0e+00

5e+06

1e+07

(a) Set A

Frequency

0.01

0.02

0.03

0.04

Frequency

0.01

0.02

0.03

0.04

-1e+07

0e+00

1e+07

2e+07

3e+07

4e+07

(b) Set B

Frequency

0.01

0.02

0.03

0.04

Frequency

0.01

0.02

0.03

0.04

0.0e+00

5.0e+06

1.0e+07

1.5e+07

Frequency

0.01

0.02

0.03

0.04

Frequency

0.01

0.02

0.03

0.04

-1e+07

0e+00

1e+07

2e+07

3e+07

(d) Set D

Figure 3: The plots of functional covariance of power spec-

tra for data sets A (Normal: Eyes Closed), B (Normal: Eyes

Open), C (Non-epileptogenic zone) and D (Epileptogenic

zone), respectively.

3 RESULTS

In order to demonstrate the application of the pro-

posed method to epilepsy diagnosis, we use a

set of EEG signals coming from healthy volun-

teers and from patients during seizure-free inter-

vals. This database is from the University of

Bonn, Germany (http://epileptologie-bonn.de/cms/

front content.php?idcat=193). There are four differ-

ent sets of EEG data, denoted, respectively by A, B,

C, and D. Data in sets A and B are normal signals

with eyes closed and open, respectively. Data in sets

C and D are epileptic signals coming from patients

suffering from epilepsy. Signals in the set C are col-

lected from the patients’ non-epileptogenic zone, and

signals in the set D are from the patients’ epilepto-

genic zone. Each dataset contains 100 single channel

scalp EEG segments of a 23.6 second duration. To

achieve this the EEG signals, were sampled at 173.61

Hz (i.e., T =4096).

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis

123

0.00 0.01 0.02 0.03 0.04 0.05

0 5000 10000 15000 20000 25000 30000

Frequency

Mean Signal Power

(a) Set A

0.00 0.01 0.02 0.03 0.04 0.05

10000 20000 30000 40000

Frequency

Mean Signal Power

(b) Set B

0.00 0.01 0.02 0.03 0.04 0.05

5000 10000 15000 20000 25000

Frequency

Mean Signal Power

0.00 0.01 0.02 0.03 0.04 0.05

10000 15000 20000 25000

Frequency

Mean Signal Power

(d) Set D

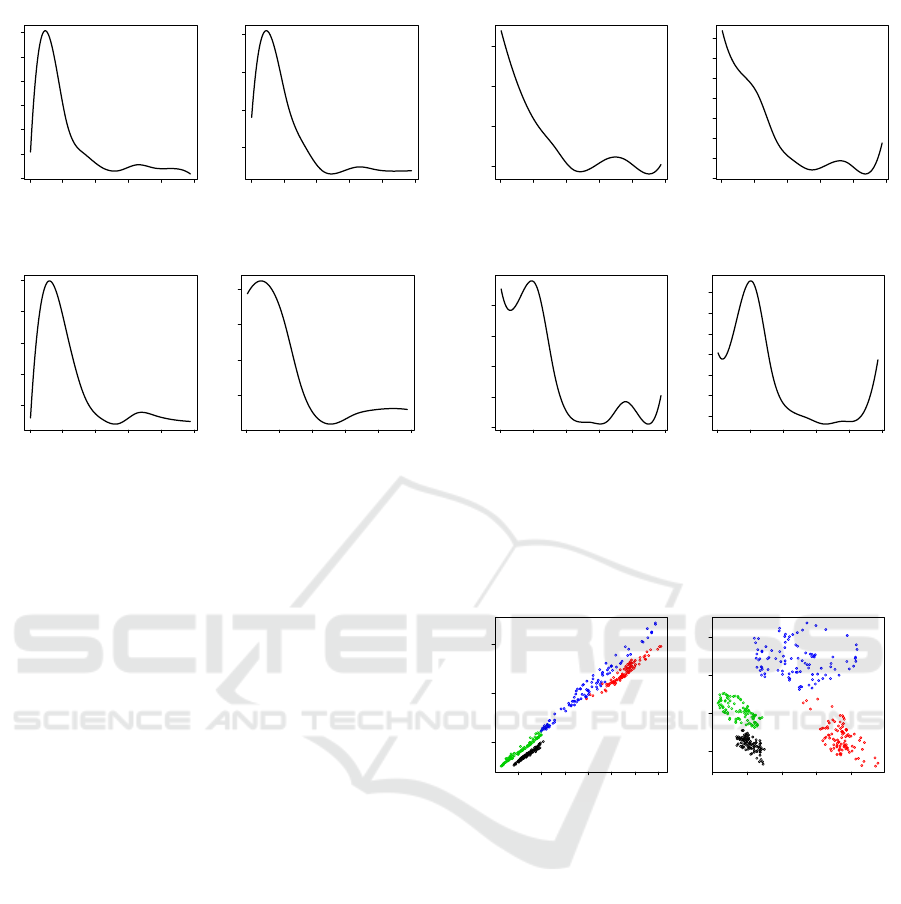
Figure 4: The plots of functional mean power spectra for

data sets A (Normal: Eyes Closed), B (Normal: Eyes

Open), C (Non-epileptogenic zone) and D (Epileptogenic

zone), respectively.

From the results displayed in Figure 2, one can

see that the smoothed signal power spectra behave

similarly for both signals from healthy people (sets

A and B) and signals from patients, which were col-

lected from a non-epileptogenic zone (set C). How-

ever, there are still some differences that we can see

among the graphs. This may suggest that further clas-

siﬁcation is needed based on these power spectra to

recognize the differences hidden in the power spectra.

Also, one can see that the power spectra of signals

collected from patients’ epileptogenic zone (set D)

are more volatile and look different from the signals

of healthy people. However, they share some com-

monalities with signals from the set C. The graphical

dispay offers some evidence that suitable clustering

methods may differentiate these types of signals suc-

cessfully.

Many clustering methods, including PCA are ap-

plied to the variance-covariance data matrix to recog-

nize the differences among different groups of data.

Therefore, we further examine the auto-covariance

data matrices for each set of signals. The results dis-

played in Figure 3 show that the auto-covariances are

signiﬁcant only at low-frequency values. This sug-

gests that it may be sufﬁcient to extract features from

small signal windows only. Thus, the focus on more

dominant powers within the spectral domain may lead

to a dimension reduction and this expectation is con-

ﬁrmed by our results displayed in Figure 1.

0.00 0.01 0.02 0.03 0.04 0.05

500 1000 1500 2000

Frequency

Signal Power Std

(a) Set A

0.00 0.01 0.02 0.03 0.04 0.05

500 1000 1500 2000 2500 3000 3500 4000

Frequency

Signal Power Std

(b) Set B

0.00 0.01 0.02 0.03 0.04 0.05

500 1000 1500 2000 2500

Frequency

Signal Power Std

0.00 0.01 0.02 0.03 0.04 0.05

2000 2500 3000 3500 4000 4500 5000

Frequency

Signal Power Std

(d) Set D

Figure 5: The plots of the functional standard deviations

of power spectra for data sets A (Normal: Eyes Closed), B

(Normal: Eyes Open), C (Non-epileptogenic zone) and D

(Epileptogenic zone), respectively.

7.0e+06 8.0e+06 9.0e+06 1.0e+07 1.1e+07 1.2e+07 1.3e+07

1500000 2000000 2500000

Probe Values based on Mean

Probe Values based on Std

(a) Functional Probes

-1000 -500 0 500 1000

-500 0 500 1000

First PC scores

2nd PC scores

(b) PC scores

Figure 6: The extracted probe values using the functional

mean and the functional standard deviation of power spec-

trum of signals of the Set D as the functional probe for

data sets A (Normal: Eyes Closed, Black), B (Normal:

Eyes Open, Red), C (Non-epileptogenic zone, Green) and

D (Epileptogenic zone, Blue) are displayed in (a). The plot

for extracted principal component scores for ﬁrst two com-

ponents of power spectra for data sets A (Normal: Eyes

Closed, Black), B (Normal: Eyes Open, Red), C (Non-

epileptogenic zone, Green) and D (Epileptogenic zone,

Blue) are displayed in (b).

In Figures 4 and 5, the functional mean and the

functional standard deviation are reported for each set

of signals. In these ﬁgures, we observe the strong

commonalities and similarities among the respective

functional statistics of the sets A, B, and C, but these

statistics look different from the ones of the set D.

This may imply a different nature of EEG signals

among the patients and non-patients (including sig-

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

124

2 4 6 8 10

0e+00 1e+05 2e+05 3e+05 4e+05

Principal Components

Eigenvalues

(a) Eigenvalues

2 4 6 8 10

0.6 0.7 0.8 0.9 1.0

Principal Components

Variance Proportion

(b) Cumulative Variance

0.00 0.01 0.02 0.03 0.04 0.05

5000 10000 15000 20000 25000 30000

Frequency

mean value

0.00 0.01 0.02 0.03 0.04 0.05

-10 -5 0 5 10 15

Frequency

values

(d) First Three Harmonics

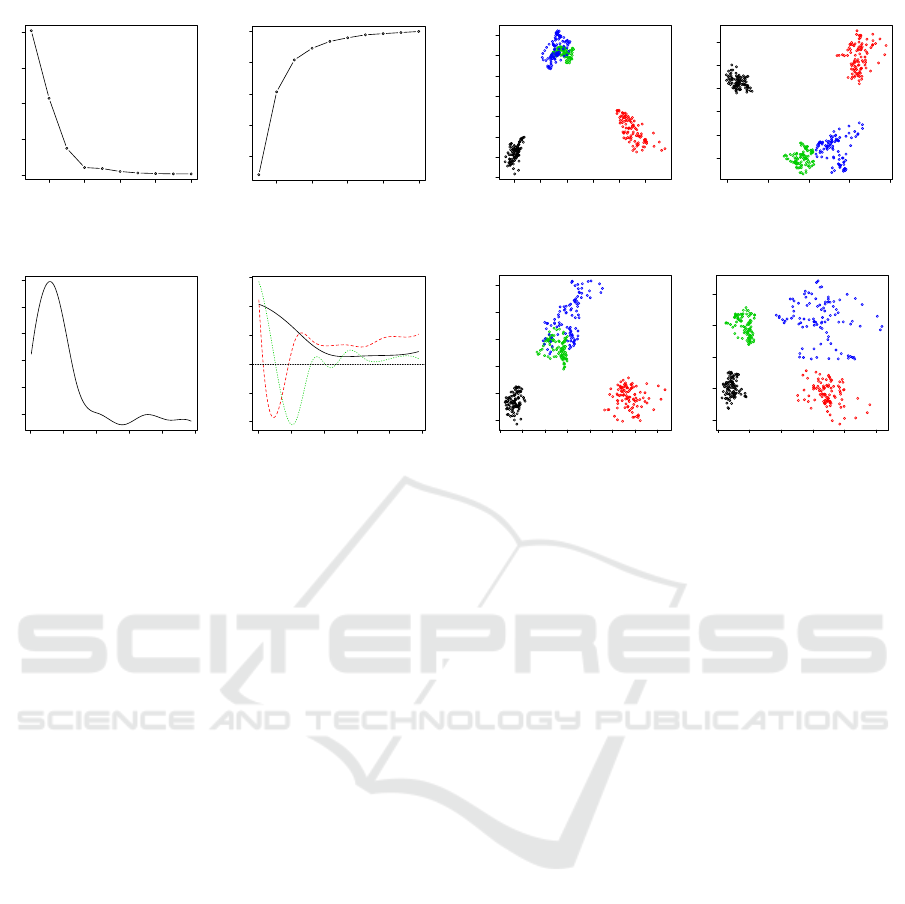
Figure 7: The results of principal components of power

spectra including eigenvalues, variance proportion, overall

functional mean and the ﬁrst three eigenfunctions. The ﬁrst

eigenfunction is in black, the second eigenfunction is in red

and the third one is in green.

nals from non-epileptogenic zone). Also, we observe

that the functional variation at high frequency is much

higher for patitents’ data, particularly for the set D. To

further reduce the dimensionality of the power spec-

trum and its functional mean and its functional stan-

dard deviation, the functional probe values are calcu-

lated based on the inner product of a selected func-

tional mean and a given signal power spectrum. The

results using functional standard deviation as a weight

function are also obtained. In our study, the best re-

sults, in terms of separability of features, are the ones

that use the functional mean and the functional stan-

dard deviation calculated from the set D. Using these

two functional probes, we extract a two-dimensional

feature vector from a given signal power spectrum.

The Figure 6 (a) clearly display the pattern, which

shows a great separability of extracted features (i.e.,

functional probe values), due to the dimension reduc-

tion. We also see that the relationship between these

two features seem to be linear for all cases. This

implies that the feature variation within each group

might not have been maximized, due to the pre-ﬁxed

functional probes. When compared to the results ob-

tained by PCA, we conﬁrm that indeed this is the case.

Principal component extractions aim at obtaining

a set of scores, so that, further investigation can be

done by using them. Our goal is to obtain a set of

principal components scores that form clusters for dif-

-2000 -1000 0 1000 2000 3000

-2000 -1500 -1000 -500 0 500 1000 1500

First PC scores

2nd PC scores

(a) K=200

-2000 -1000 0 1000 2000

-1000 -500 0 500 1000 1500

First PC scores

2nd PC scores

(b) K = 100

-1500 -1000 -500 0 500 1000 1500 2000

-1000 -500 0 500 1000 1500

First PC scores

2nd PC scores

-1000 -500 0 500 1000 1500

-1000 -500 0 500 1000

First PC scores

2nd PC scores

(d) K = 25

Figure 8: The Evolution of extracted ﬁrst two principal

component scores of power spectra under different choices

of K for data sets A (Normal: Eyes Closed, Black), B (Nor-

mal: Eyes Open, Red), C (Non-epileptogenic zone, Green)

and D (Epileptogenic zone, Blue).

ferent groups of signals. The obtained principal com-

ponent scores are reported in Figure 6 (b) under the

selection of K = 10, which is considered to be the op-

timal value in terms of feature separability. From the

displayed results, we can see that in clustering power

spectra of the four sets of signals the functional PCA

is more successful than the functional mean and the

functional standard deviation as the probes, as can be

seen from the previously discussed results. We no-

tice that, the principal components scores of power

spectra are completely separable from other groups.

Overall, the principal components scores form bet-

ter into clusters that have clear centroids and more

homogenous variations. This is particularly impor-

tant and useful for model-based classiﬁcation meth-

ods such as Gaussian mixture models. The Figure 7

displays more results of the principal component anal-

ysis including eigvenvalues, cumulative variance pro-

portion, functional grand mean and functional prin-

cipal components. The displayed results show that

the ﬁrst three principal components are dominant in

terms of explanation of data variation. The functional

grand mean reﬂects, mainly, the pattern of the power

spectra of the sets A, B, and C. These sets have ei-

ther signals from healthy people or signals from a

non-epileptogenic zone of a patient. The main char-

acteristics of power spectra of the set D are reﬂected

in both second and third principal components, while

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis

125

the ﬁrst principal component captures the functional

grand mean. This helps to explain why by taking the

functional mean and the functional standard deviation

of power spectrum from set D as functional probes

also produce separable functional probe values.

We further investigate the effect of the number

of basis functions (i.e., K) on the separability of

extracted signal features (i.e., principal component

scores of power spectra). The obtained results are

displayed in Figure 8. We observe that the proposed

method is highly successful in separating the artifacts

(i.e., open/closed eyes) as the results did not depend

on how the number of basis functions was selected.

The feature separability increases with the decrease of

K, i.e., the number of basis functions. This may sug-

gest that the sparsity in approximation of the signal

power spectra plays an important role in the success

of applying functional principal component analysis.

When K=200, the extracted features for epileptic sig-

nals overlap signiﬁcantly. This overlapping changes

when K decreases, and features start to be fully sepa-

rable when K is relatively small, for example, around

25. However, the overall separability between healthy

and epileptic signals is not affected by the number of

basis functions.

4 CONCLUDING REMARKS

Clustering and classiﬁcation of highly dimensional

data are important tasks in pattern recognition and ar-

tiﬁcial intelligence. To be successful in using machine

learning techniques, including clustering and classiﬁ-

cation, dimension reduction of data is a key approach.

In this work, we have conisdered an approach that

ﬁrst transforms signals to the spectral domain and ob-

tains their power spectra. Next, we have applied the

functional data analysis techniques to further investi-

gate the charateristics of the signals. We have demon-

strated that functional data analysis in spectral domain

is useful for understanding the key features of differ-

ent types of EEG signals. Especially, the extracted

features, using functional principal component anal-

ysis, can be used for classiﬁcation of different types

of EEG signals. Also we have investigated the effect

of sparsity on the performance of separating signal

features. The obtained results demonstrate that the

proposed method may be useful for an epilepsy diag-

nosis. Future work will focus on the study of wavelet

spectral domain functional PCA and its application to

clustering random signals.

ACKNOWLEDGEMENT

The authors acknowledges partial support from

NSERC (Natural Sciences and Engineering Research

Council of Canada).

REFERENCES

Alickovic, E., Kevric, J., and Subasi, A. (2018). Perfor-

mance evaluation of empirical mode decomposition,

discrete wavelet transform, and wavelet packed de-

composition for automated epileptic seizure detection

and prediction. Biomedical Signal Processing and

Control, 39:94–102.

Bouveyron, C., Girard, S., and Schmid, C. (2007). High-

dimensional data clustering. Computational Statistics

& Data Analysis, 52(1):502–519.

De Boor, C., De Boor, C., Math

ematicien, E.-U., De Boor,

C., and De Boor, C. (1978). A practical guide to

splines, volume 27. Springer-Verlag New York.

Fergus, P., Hussain, A., Hignett, D., Al-Jumeily, D., Abdel-

Aziz, K., and Hamdan, H. (2016). A machine learning

system for automated whole-brain seizure detection.

Applied Computing and Informatics, 12(1):70–89.

Gandhi, T., Panigrahi, B. K., and Anand, S. (2011). A com-

parative study of wavelet families for eeg signal clas-

siﬁcation. Neurocomputing, 74(17):3051–3057.

Garcia, G. N., Ebrahimi, T., and Vesin, J.-M. (2003).

Support vector eeg classiﬁcation in the fourier and

time-frequency correlation domains. In Neural En-

gineering, 2003. Conference Proceedings. First Inter-

national IEEE EMBS Conference on, pages 591–594.

IEEE.

Jimenez, L. O. and Landgrebe, D. A. (1998). Supervised

classiﬁcation in high-dimensional space: geometrical,

statistical, and asymptotical properties of multivariate

data. IEEE Transactions on Systems, Man, and Cyber-

netics, Part C (Applications and Reviews), 28(1):39–

54.

Kriegel, H.-P., Kr

oger, P., and Zimek, A. (2009). Clustering

high-dimensional data: A survey on subspace cluster-

ing, pattern-based clustering, and correlation cluster-

ing. ACM Transactions on Knowledge Discovery from

Data (TKDD), 3(1):1.

Li, D., Pedrycz, W., and Pizzi, N. J. (2005). Fuzzy wavelet

packet based feature extraction method and its appli-

cation to biomedical signal classiﬁcation. IEEE Trans-

actions on biomedical engineering, 52(6):1132–1139.

Liang, S.-F., Wang, H.-C., and Chang, W.-L. (2010). Com-

bination of eeg complexity and spectral analysis for

epilepsy diagnosis and seizure detection. EURASIP

Journal on Advances in Signal Processing, 2010:62.

Lima, C. A., Coelho, A. L., and Chagas, S. (2009). Auto-

matic eeg signal classiﬁcation for epilepsy diagnosis

with relevance vector machines. Expert Systems with

Applications, 36(6):10054–10059.

ICPRAM 2019 - 8th International Conference on Pattern Recognition Applications and Methods

126

Nyan, M., Tay, F., Seah, K., and Sitoh, Y. (2006). Classiﬁ-

cation of gait patterns in the time–frequency domain.

Journal of biomechanics, 39(14):2647–2656.

Phinyomark, A., Phukpattaranont, P., and Limsakul, C.

(2012). Feature reduction and selection for emg sig-

nal classiﬁcation. Expert Systems with Applications,

39(8):7420–7431.

Qazi, K. I., Lam, H., Xiao, B., Ouyang, G., and Yin, X.

(2016). Classiﬁcation of epilepsy using computational

intelligence techniques. CAAI Transactions on Intel-

ligence Technology, 1(2):137–149.

Ramsay, J. (2005). Functional data analysis. Encyclopedia

of Statistics in Behavioral Science.

Ramsay, J. O. and Silverman, B. W. (2007). Applied

functional data analysis: methods and case studies.

Springer.

Subasi, A. and Gursoy, M. I. (2010). Eeg signal classiﬁca-

tion using pca, ica, lda and support vector machines.

Expert systems with applications, 37(12):8659–8666.

Truong, N. D., Kuhlmann, L., Bonyadi, M. R., Yang, J.,

Faulks, A., and Kavehei, O. (2017). Supervised learn-

ing in automatic channel selection for epileptic seizure

detection. Expert Systems with Applications, 86:199–

207.

Unser, M., Aldroubi, A., Eden, M., et al. (1993). B-spline

signal processing: Part i theory. IEEE transactions on

signal processing, 41(2):821–833.

Wang, J.-L., Chiou, J.-M., and M

uller, H.-G. (2016). Func-

tional data analysis. Annual Review of Statistics and

Its Application, 3:257–295.

Yu, L. and Liu, H. (2003). Feature selection for high-

dimensional data: A fast correlation-based ﬁlter solu-

tion. In Proceedings of the 20th international confer-

ence on machine learning (ICML-03), pages 856–863.

Zhang, Z., Xu, Y., Yang, J., Li, X., and Zhang, D. (2015).

A survey of sparse representation: algorithms and ap-

plications. IEEE access, 3:490–530.

Feature Extraction of Epileptic EEG in Spectral Domain via Functional Data Analysis

127