Security Analysis and Efficient Implementation
of Code-based Signature Schemes
Partha Sarathi Roy
1
, Kirill Morozov
2
, Kazuhide Fukushima
1
, Shinsaku Kiyomoto
1
and Tsuyoshi Takagi
3
1
Information Security Laboratory, KDDI Research, Inc., 2-1-15 Ohara, Fujimino-shi, Saitama 356-8502, Japan
2
Department of Computer Science and Engineering, University of North Texas, Denton, TX 76207, U.S.A.
3
Department of Mathematical Informatics, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan
Keywords:
Post-quantum Cryptography, Code-based Cryptography, Signature Scheme, Fiat-Shamir Transformation,
Identification Scheme.
Abstract:
In this paper, we derive code-based signature schemes using Fiat-Shamir transformation on code-based zero-
knowledge identification schemes, namely the Stern scheme, the Jain-Krenn-Pietrzak-Tentes scheme, and the
Cayrel-Veron-El Yousfi scheme. We analyze the security of these code-based signature schemes and derive the
security parameters to achieve the 128-bit level security. Furthermore, we implement these signature schemes
and compare their performance on a PC.
1 INTRODUCTION
Digital signatures are essential components of IT-
security solutions. Security of the schemes, already
used in practice, relies on the number-theoretic hard-
ness assumptions. Unfortunately, these problems are
known to be solvable in polynomial time on quan-
tum computers using Shor’s algorithm (Shor, 1994).
Hence, quantum computers would be able to break
popular cryptosystems such as RSA or ElGamal (in-
cluding its elliptic-curve variant) in polynomial time.
Given these circumstances, it is important to consi-
der the transition to post-quantum digital signature
schemes. In this work, we focus on the practical use
of code-based signature scheme as one of the post-
quantum candidates.
CFS (Courtois et al., 2001), KKS (Kabatianskii
et al., 1997), and their variants are the most celebrated
code-based signature schemes. Unfortunately, there
are various drawbacks in respect of security, computa-
tion time, key or signature size. The CFS scheme was
proven existentially unforgeable under chosen mes-
sage attack (EUF-CMA) by Dallot (Dallot, 2008) un-
der the hardness of the Goppa-Parametrized Boun-
ded Decoding problem and the Goppa-Code Distin-
guishing (GD) problem. Even with the existence of
a distinguisher (Faug
´
ere et al., 2011) for the Goppa
codes of high rate, a simple modification can pro-
vide Strong EUF-CMA security for the CFS signature
(Morozov et al., 2018). However, from the practical
prespective, signing time of CFS signature is somew-
hat high due to the difficulty of finding decodable syn-
dromes. Debris-Alazard et al. (Debris-Alazard et al.,
2017) exposed a problem with the recently introdu-
ced SURF signature scheme. The main drawback of
the KKS-like signature schemes is their security as
shown by Otmani et al. (Otmani and Tillich, 2011).
Therefore, we will explore the time-tested approach
to signature schemes via the Fiat-Shamir transform
over zero-knowledge identification schemes.
Our Contribution. In this paper, we study code-
based signature schemes via Fiat-Shamir transforma-
tion on zero-knowledge (ZK) identification schemes.
The Fiat-Shamir transform seems to be the promi-
sing avenue to have both efficient and secure code-
based signature schemes. We chose to study and
compare zero-knowledge identification schemes by
Stern (Stern, 1994), Jain et al. (Jain et al., 2012) and
Cayrel et al. (Cayrel et al., 2010). Note that Jain
et al. (Jain et al., 2012) pointed out a flaw in the
proof of zero-knowledge property of Veron’s code-
based identification scheme (V
´
eron, 1997), and so
Jain et al. provided an alternative scheme which is
indeed ZK. As security assumption, Jain et al. used
the so-called Exact-LPN (xLPN) problem (Jain et al.,
Roy, P., Morozov, K., Fukushima, K., Kiyomoto, S. and Takagi, T.
Security Analysis and Efficient Implementation of Code-based Signature Schemes.
DOI: 10.5220/0007259102130220
In Proceedings of the 5th International Conference on Information Systems Security and Privacy (ICISSP 2019), pages 213-220
ISBN: 978-989-758-359-9
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
213

2012), which is, in fact, identical to the general deco-
ding problem considered both in Veron’s paper, and
in this work.
1
There are some existing studies on
the efficient implementation of Stern’s scheme by Ga-
borit et al. (Gaborit and Girault, 2007), and Cayrel
et al. (Cayrel et al., 2008). El Yousfi et al. (Ala-
oui et al., 2013) have studied the implementations of
Stern (Stern, 1994), Veron (V
´
eron, 1997) and Cay-
rel et al. (Cayrel et al., 2010). However, these works
show system parameters for identification schemes
that achieve 80-bit security. Due to the growing power
of modern computing systems, it seems preferable to
investigate the performance of the signature schemes
for 128-bit security benchmark. We implement in C
the digital signatures based on Stern’s (Stern, 1994),
Jain et al.’s (Jain et al., 2012) and Cayrel et al.’s (Cay-
rel et al., 2010) identification schemes, and compare
their performance on a PC.
2 PRELIMINARIES
2.1 Notations
We will use the following notations throughout the
article.
• {0,1}
∗
: bit string of arbitrary length.
• F
q
: Galois field of q elements.
• F
n
q
: Vector with n elements over F
q
.
• F
m×n
q
: Matrix with m rows and n columns whose
elements are in F
q
.
• wt(c): Hamming weight of string c, i.e., the num-
ber of non-zero positions of the string.
• k: Concatenation of strings. We see a string as a
column vector.
2.2 Zero-knowledge Identification
Scheme
An identification scheme consists of three probabilis-
tic, polynomial-time algorithms (G,P,V ) such that:
• The randomized key generation algorithm G takes
as input the security parameter 1
λ
. It outputs a
pair of keys (pk,sk), where pkis called the public
key and sk is called the private key. We assume
1
Jain et al. presented the ZK identification scheme ba-
sed on the standard LPN problem as well, but it has higher
soundness error as compared to the xLPN-based one. Hence
it would result in signatures of larger size, and hence it is out
of the scope of this work.
the security parameter is implicit in both pk and
sk.
• P and V are interactive protocols. The prover al-
gorithm P takes as input a private key sk and
the verification algorithm V takes as input a pu-
blic key pk. At the conclusion of the protocol, V
outputs 1 or ⊥.
It holds the following properties:
Completeness: [P(sk),V (pk)] = 1.
Honest V always accepts honest P.
Soundness: Pr([P
∗
,V (pk)] = 1) = negl (λ).
Cheating P
∗
(not knowing sk) is rejected with
overwhelming probability.
Zero-knowledge: [P(sk),V
∗
(pk)] ≈ [Sim,V
∗
(pk)].
Cheating V
∗
learns nothing about sk.
2.3 Digital Signature
A digital signature scheme Σ = (Key Generation,
Signature Generation, Signature Verification) is
consists of three algorithms.
Key Generation: The key generation algorithm ta-
kes a security parameter 1
λ
and outputs a pair of
keys (pk, sk).
Signature Generation: The signature generation al-
gorithm takes a message m and a private key skas
inputs and outputs a signature σ on the message
m.
Signature Verification: The signature verification
algorithm takes as input a public key pk, a mes-
sage m and a signature σ, and outputs a bit deno-
ting accept or reject, respectively.
The standard security notion for a signature
scheme is existential unforgeability against chosen
message attack (EUF-CMA): The forger gets a public
key from a challenger who generates a key pair (sk,
pk). The forger can query a signing oracle on polyno-
mially many messages m
i
hereby obtaining signatures
σ
i
. The forger can also issue a hash query and obtains
its hash value. We say that the forger wins the EUF-
CMA game, if the forger successfully outputs a pair
(m
∗
,σ
∗
), where σ
∗
is a valid signature of a message
m
∗
under the private key with the restriction that m
∗
has never appeared in the query phase.
2.4 Security Assumptions
An [n,k] Linear Code C is a subspace of dimension k
of the vector space F
n
q
. A linear code can be described
by its Parity-check matrix H. The parity-check matrix
describes the code as follows:
x ∈C ⇔ Hx = 0 (∀x ∈F
n
q
).
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
214

The product Hx is known as the syndrome of the vec-
tor x.
Definition 1. Gilbert-Varshamov Bound:
Let C be an [n,k] linear code over F
q
. The Gilbert-
Varshamov (GV) Distance is the largest integer ω
such that
k
n
= 1 −H
q

ω
n

,
where H
q
is the q-ary entropy function
Now, we describe the main hard problems on
which the security of code-based signature schemes,
presented in the paper, relies.
Definition 2. Syndrome Decoding Problem
(SDP) (Augot et al., 2003):
Input: a matrix H ∈ F
(n−k)×n
2
, a positive integer ω,
and a vector s ∈ F
n−k
2
.
Output: a codeword x such that wt(x) = ω
0
where
0 < ω
0
≤ ω and Hx = s.
This problem is NP-complete (Berlekamp et al.,
1978), which means that at least some instances of
the problem are difficult. However, it is a common be-
lief that they should be difficult on average (for well-
chosen parameter ranges), which means that random
instances are difficult. It is also proved that there ex-
ists a unique solution to SDP if the weight ω is below
the GV Bound.
Definition 3. General Decoding Problem (GDP):
Input: a matrix G ∈F
k×n
2
, a non negative integer ω,
and a vector y ∈ F
n
2
.
Output: a pair (m,e) ∈F
k
2
×F
n
2
such that wt(e) = ω
0
where 0 < ω
0
≤ ω and mG ⊕e = y.
An extension of SDP over arbitrary finite field is
as follows:
Definition 4. q-ary Syndrome Decoding Problem (q-
SDP) (Augot et al., 2003):
Input: a matrix H ∈F
(n−k)×n
q
, a non negative integer
ω and a vector s ∈ F
n−k
q
.
Output: a codeword x such that of wt(x) = ω
0
where
0 < ω
0
≤ ω and Hx = s.
q-SDP is proven to be NP-hard by S.Barg (Barg,
1994).
Definition 5. Exact Learning Parity with Noise
(xLPN) (Jain et al., 2012):
The the decisional-xLPN problem is (n,t,ε)-hard if
for every distinguisher D running in time t




Pr
s,A,e
[D(A,As ⊕e) = 1] −Pr
A,r
[D(A,r) = 1]




≤ ε
where s ←$ F
n
2
, e ←$ {0,1}
n
such that wt(e) = ω,
r ←$ F
k
2
and A ←$ F
k×n
2
.
3 SIGNATURE SCHEME
In this section, we will derive the signature scheme
from code-based zero-knowledge identification sche-
mes. Using Fiat-Shamir transformation (Pointcheval
and Stern, 2000), we can derive signature schemes
from the Stern (Stern, 1994) and Jain et al. (Jain et al.,
2012) identification schemes. We need to use the ex-
tended version of Fiat-Shamir transformation (Alaoui
et al., 2012) to derive a signature scheme from Cayrel
et al.’s scheme (Cayrel et al., 2010).
3.1 Stern Signature Scheme.
System Parameters. The Stern signature scheme
uses the following system parameters:
• Positive integer n (length of codeword),
• Positive integer k such that k < n (dimension of
the code),
• Positive integer ω (minimum distance of the
code),
• Matrix H ∈ F
(n−k)×n
2
sampled randomly.
• random oracle: h : {0,1}
∗
→ {0,1}
∗
• random oracle: O : {0,1}
∗
→ {0,1,2}
Key Generation. The key generation algorithm
outputs the pair of the private key s and public key
y.
1. Sample a vector s ∈ F
n
2
such that wt(s) = ω.
2. Calculate a vector y ∈ F
n−k
2
as y = Hs.
3. Output private key s and public key y.
Signature Generation. Takes as input private key s
and a message m, and output Sig. The detailed algo-
rithm is described in Algorithm 3.
Signature Verification. Takes as input public key y,
message m, Sig. Compute b
i
← O(mkc
i
) and output
1 if the following respective equation is valid for all
1 ≤ i ≤ δ:













Check c
i,0
= h(σ
i
kHu
i
) and c
i,1
= σ
i
(u
i
). (b
i
= 0)
Check c
i,0
= h(σ
i
kH(u
i
⊕s) ⊕y) and
c
i,2
= h(σ
i
(u
i
⊕s)). (b
i
= 1)
Checkc
i,1
= σ
i
(u
i
),c
i,2
= h(σ
i
(u
i
) ⊕σ
i
(s)),
and wt(σ
i
(s)) = ω. (b
i
= 2)
,
or ⊥ otherwise.
Security Analysis and Efficient Implementation of Code-based Signature Schemes
215

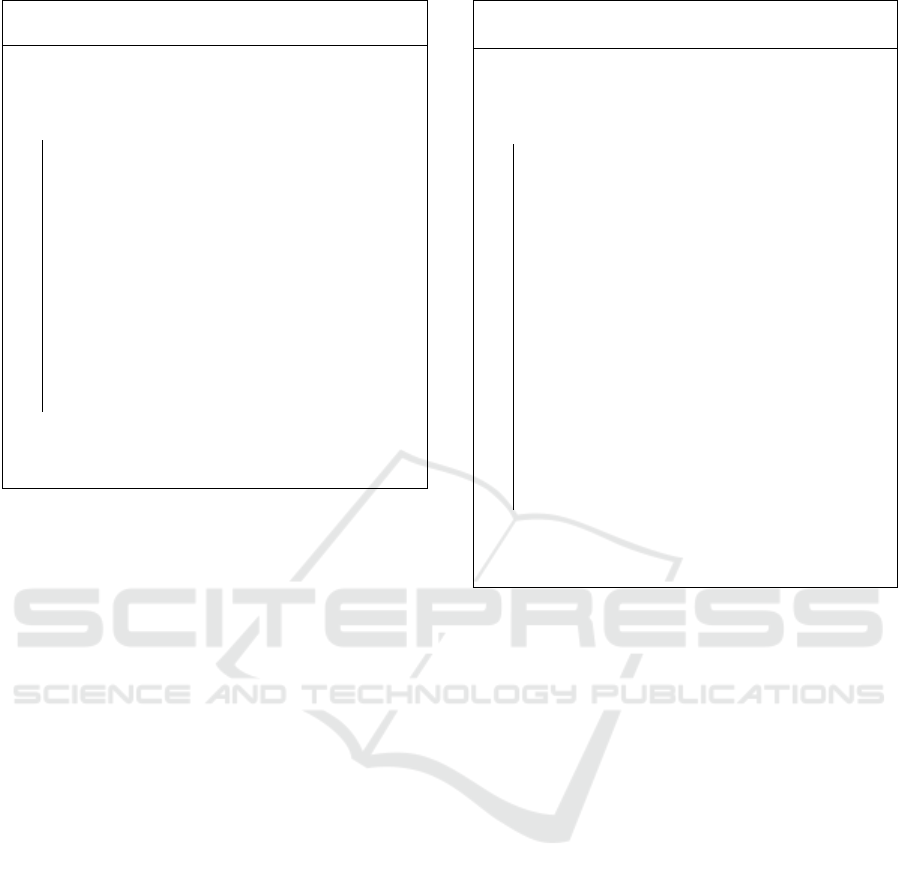
Algorithm 1: Signature Generation in Stern signa-
ture scheme.
Input: Private key s, Message m, and System
parameters
Output: Signature Sig
for i ← 0 to δ −1 do
1 u
i
←$ F
n
2
;
2 σ
i
←$ S
n
;
3 c
i,0
← h(σ
i
kHu
i
);
4 c
i,1
← σ
i
(u
i
);
5 c
i,2
← h(σ
i
(u
i
⊕s));
6 c
i
= (c
i,0
kc
i,1
kc
i,2
);
7 b
i
= O(mkc
i
);
8 rsp
i
←





σ
i
ku
i
(b
i
= 0)
σ
i
k(u
i
⊕s) (b
i
= 1)
σ
i
(u
i
)kσ
i
(s) (b
i
= 2)
;
9 sig
i
= c
i
krsp
i
;
end
10 Sig ←sig
0
ksig
1
k···ksig
δ−1
;
return Sig;
3.2 Jain et al. Signature Scheme
In this section, we will derive the signature scheme
from the identification scheme of (Jain et al., 2012).
We will modify the design a little, without any secu-
rity breach, for the sake of fast implementation.
System Parameters. The signature scheme uses
the system parameters as in Stern signature scheme
apart from random sampling of A ∈ F
k×n
2
instead of
H ∈ F
(n−k)×n
2
.
Key Generation. The key generation algorithm
outputs the pair of the private key e and public key
y.
1. Sample (s,e) ←$ F
k
2
×F
n
2
such that wt(e) = ω.
2. Calculate y = sA ⊕e.
3. Output private key e and public key y.
Signature Generation. The signature generation
algorithm takes private key e and a message m, output
Sig, and system parameters as inputs. Algorithm 2
describes the detailed algorithm.
Signature Verification. The signature verification
algorithm takes as input public key y, message m, Sig,
and system parameters. It computes b
i
← O(mkc
i
)
and outputs 1 if the following respective equation is
valid for all 0 ≤ i ≤ δ −1:
Algorithm 2: Signature Generation in Jain et al.
signature scheme.
Input: Private key e, Message m, and System
parameters
Output: Signature Sig
for i ← 0 to δ −1 do
1 u
i
←$ F
n
2
;
2 v
i
←$ F
k
2
;
3 σ
i
←$ S
n
;
4 y
i,0
← v
i
A ⊕u
i
;
5 c
i,0
← h(σ
i
ky
i,0
);
6 y
i,1
← σ
i
(u
i
);
7 c
i,1
← h(y
i,1
);
8 y
i,2
← σ
i
(u
i
⊕e);
9 c
i,2
← h(y
i,2
);
10 c
i
← c
i,0
kc
i,1
kc
i,2
;
11 b
i
← O(mkc
i
);
12 rsp
i
←





σ
i
ky
i,0
ky
i,1
(b
i
= 0)
σ
i
ky
i,0
ky
i,2
(b
i
= 1)
y
i,1
ky
i,2
(b
i
= 2)
;
13 sig
i
← c
i
krsp
i
;
end
14 Sig ←sig
0
ksig
1
k···ksig
δ−1
;
return Sig;

































Check c
i,0
← h(σ
i
ky
i,0
),
c
i,1
← h(y
i,1
), (b
i
= 0)
y
i,0
⊕σ
−1
i
(y
i,1
) = xA, for some x and σ
i
∈ S
n
Check c
i,0
← h(σ
i
ky
i,0
),
c
i,2
← h(y
i,2
), (b
i
= 1)
and y
i,0
⊕σ
−1
i
(y
i,2
) ⊕y = xA,for some x
Check c
i,1
← h(y
i,1
),
c
i,2
← h(y
i,2
), (b
i
= 2)
and wt(y
1,i
⊕y
2,i
) = ω
,
or ⊥ otherwise.
3.3 Cayrel et al. Signature Scheme
To present the Cayrel et al., signature scheme, first we
introduce a special transformation that will be used in
the scheme.
Definition 6. Let σ ∈S
n
and γ = (γ
1
,··· , γ
n
) ∈ (F
∗
q
)
n
such that γ
i
6= 0 for all i. The transformation Π
γ,σ
is
defined as follows:
Π
γ,σ
:F
n
q
→ F
n
q
v 7→

γ
σ[0]
v
σ[0]
,γ
σ[1]
v
σ[1]
,··· , γ
σ[n−1]
v
σ[n−1]

.
Notice that this transformation is linear transfor-
mation, and satisfies Π
γ,σ
(v+w) = Π
γ,σ
(v)+Π
γ,σ
(w)
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
216

and Π
γ,σ
(αv) = αΠ
γ,σ
(v) for all v, w, α ∈ F
q
. Furt-
hermore, the transformation preserves the Hamming
weight of the vector.
Now, we are in the state to present the signature
scheme:
System Parameters. The signature scheme uses
the following system parameters:
• Positive integer n (length of codeword),
• Positive integer k such that k < n (dimension of
the code),
• Positive integer ω (minimum distance of the
code),
• Matrix H ∈ F
(n−k)×n
q
sampled randomly,
• Random oracle h : {0,1}
∗
→ {0,1}
∗
,
• Random oracle O
1
: {0,1}
∗
→ F
n
q
,
• Random oracle O
2
: {0,1}
∗
→ {0,1}.
Key Generation. The key generation algorithm
outputs the pair of the private key s and public key
y.
1. Sample a vector s ∈ F
n
q
such that wt(s) = ω.
2. Calculate a vector y ∈ F
n−k
q
as y = Hs.
3. Output private key s and public key y.
Signature Generation. The signature generation
algorithm takes as input private key s and a message
m, and output a signature Sig. The detailed algorithm
is described in Algorithm 3.
Signature Verification. The signature verification
algorithm takes public key y, message m, and signa-
ture Sig as inputs. It computes α
i
← O
1
(mkc
i
) and
b
i
← O
2
(mkc
i
kα
i
kβ
i
); then, it outputs 1 if the follo-
wing respective equation is valid for all 0 ≤i ≤δ−1:



Check c
i,0
= h(σ
i
kγ
i
kHΠ
−1
γ
i
,σ
i
(β
i
) −α
i
y) (b
i
= 0)
Check c
i,1
= h(β
i
−α
i
Π
γ
i
,σ
i
(s)kΠ
γ
i
,σ
i
(s))
and wt(Π
γ,σ
(s)) = ω (b
i
= 1)
,
or ⊥ otherwise.
4 SECURITY ANALYSIS AND
PARAMETER SELECTION
Best Known Attack: It is required to consider struc-
tural attack and key-recovery attack to measure the
security of code-based signature schemes. Due to the
Algorithm 3: Signature Generation in Cayrel et al.
signature scheme.
Input: Private key s, Message m, and System
parameters
Output: Signature Sig
for i ← 0 to δ −1 do
1 u
i
←$ F
n
q
;
2 σ
i
←$ S
n
;
3 γ
i
←$ (F
q
\{0})
n
;
4 c
i,0
← h(σ
i
kγ
i
kHu
i
);
5 c
i,1
← h(Π
γ
i
,σ
i
(u
i
)kΠ
γ
i
,σ
i
(s));
6 c
i
← c
i,0
kc
i,1
;
7 α
i
← O
1
(mkc
i
);
8 β
i
← Π
γ
i
,σ
i
(u
i
+ α
i
s);
9 b
i
← O
2
(mkc
i
kα
i
kβ
i
);
10 rsp
i
←
(
σ
i
kγ
i
(b
i
= 0)
Π
γ
i
,σ
i
(s) (b
i
= 1)
;
11 sig
i
= c
i
kβ
i
krsp
i
;
end
12 Sig ←sig
0
ksig
1
k···ksig
δ−1
;
return Sig;
use of random code only, consideration of structu-
ral attack abolish. Signature schemes, constructed by
using Fiat-Shamir transformation and it is extended
version on zero knowledge identification schemes, are
EUF-CMA secure (Pointcheval and Stern, 2000; Ala-
oui et al., 2012). Moreover, EUF-CMA security in-
cludes the security against key-recovery attack. The-
refore, to choose secure parameters, it is required to
measure the hardness of the problem, where the proof
of EUF-CMA security is reduced.
The security of the Stern and Cayrel et al. signa-
tures are reduced to the hardness of SDP and qSDP,
respectively. The most efficient known algorithm to
attack SDP is the Information Set Decoding (ISD)
algorithm by Stern (Stern, 1988). Further, there are
few many improvements over (Stern, 1988). One of
the intermediate notable improvement is by Finiasz
et al. (Finiasz and Sendrier, 2009). Further impro-
vements over (Finiasz and Sendrier, 2009) are asymp-
totic (May et al., 2011; Becker et al., 2012). So, we
have used the measurement of (Finiasz and Sendrier,
2009) to measure the hardness of SDP. The hardness
of q-ary SDP is measured by the formulation of (Nie-
buhr et al., 2017), which is the extension of (Finiasz
and Sendrier, 2009) from binary to an arbitrary finite
field.
Security of Jain et al. signature scheme is redu-
ced to the hardness of xLPN. However, in actuality,
the number of sample of the instance is small, and we
cannot apply the BKW algorithm to solve the xLPN
problem. So, the hardness is turned down to the hard-
Security Analysis and Efficient Implementation of Code-based Signature Schemes
217

Table 1: System parameters and data sizes for Stern signa-
ture scheme.
Parameter 80-bit Security 128-bit Security
Independent parameters:
n 620 1,024
δ 137 219
Derived parameters:
k 310 512
ω 68 112
Data size:
sk 620 bit 1024 bit
pk 310 bit 512 bit
Signature 93.3 kB 245 kB
Systemf param. 24.0 kB 65.5 kB
ness of the general decoding problem. We thus have
used the measurement of (Finiasz and Sendrier, 2009)
to measure the hardness.
4.1 Stern Signature Scheme
We select parameters n, k and ω so that they lie on the
GV bound i.e.,
k
n
= 1 −H
2

ω
n

, (1)
to maximize the security against attacks using the
ISD algorithm. We select k = n/2 and ω is around
0.110n. The complexity of the ISD (Finiasz and Sen-
drier, 2009) is
WF
ISD
(n,k,ω) = min
p
2l min

n
ω

,2
r

(1 −e
−1
)

r−l
ω−p

q

k+l
p

(2)
where
l = log
2
2ω
s

k
p

!
for the parameters on the GV bound, and n should
satisfy WF
ISD
(n,k,ω) > 2
λ
.
The number of rounds δ depends on a soundness
error of the underlying identification scheme. The
soundness error of the Stern identification scheme
(Stern, 1994) is 2/3. So, δ should satisfy (2/3)
δ
<
2
−λ
. System parameters and data sizes are presented
in Table 1.
4.2 Jain et al. Signature Scheme
We select parameters n, k and ω according to the
equation 1 & 2. The number of rounds δ depends on
the Soundness error of the underlying identification
scheme. Soundness error of the Jain et al. identifica-
tion scheme (Jain et al., 2012) is 2/3. So, δ should
satisfy (2/3)
δ
< 2
−λ
. System parameters and data si-
zes are presented in Table 2.
Table 2: System parameters and data sizes of Jain et al.
signature scheme.
Name 80-bit Security 128-bit Security
Independent parameters:
n 620 1,024
δ 137 219
Derived parameters:
k 310 512
ω 68 112
Data size:
sk 930 bit 1536 bit
pk 620 bit 1024 bit
Signature 95.11 kB 263 kB
System param. 24.0 kB 65.5 kB
4.3 Cayrel et al. Signature Scheme
We select parameters n, k and ω so that they lie on the
GV bound i.e.,
k
n
= 1 −H
q

ω
n

,
to maximize the security against attacks using the ISD
algorithm. We select k = n/2 and ω is around 0.380n.
The relevant formula to evaluate work factor is as
follows (Niebuhr et al., 2017):
WF
qISD
(n,k, ω,q)
= min
l,p
1
,p
2
N
p,q
(l)
√
q −1
λ
−1
q
2(q −1)l
(q

l
p
0
2

(q −1)p
0
2
+ p
2
!
×
s

k
p
1

l
p
2

(q −1)
p−1
+ K
q

k
p
1

l
p
2

(q −1)
p−1
q
l
!
where
N
p,q
(l) =
min(

n
ω

(q −1)
ω
,q
n−k
)

n−k−l
ω−p

k
p
1

i
p
2

(q −1)
ω
,
p = p
1
+ p
2
, p
0
2
= bp
2
/2c, λ
q
= 1 −e
−1
≈ 0.63 and
bp
2
/2c means maximum integer that does not exceed
p
2
/2. n should satisfy WF
ISD
(n,k,ω) > 2
λ
.
The number of rounds δ depends on the Soundness
error of the underlying identification scheme. Sound-
ness error of the Cayrel et al. identification scheme
(Cayrel et al., 2010) is 1/2. So, δ should satisfy
(1/2)
δ
< 2
−λ
. System parameters and data sizes are
presented in Table 3.
5 IMPLEMENTATIONS
We implement the Stern, Jain et al. and Cayrel et al.
signature schemes with 128-bit level security in C lan-
guage. Execution time and data sizes are presented in
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
218

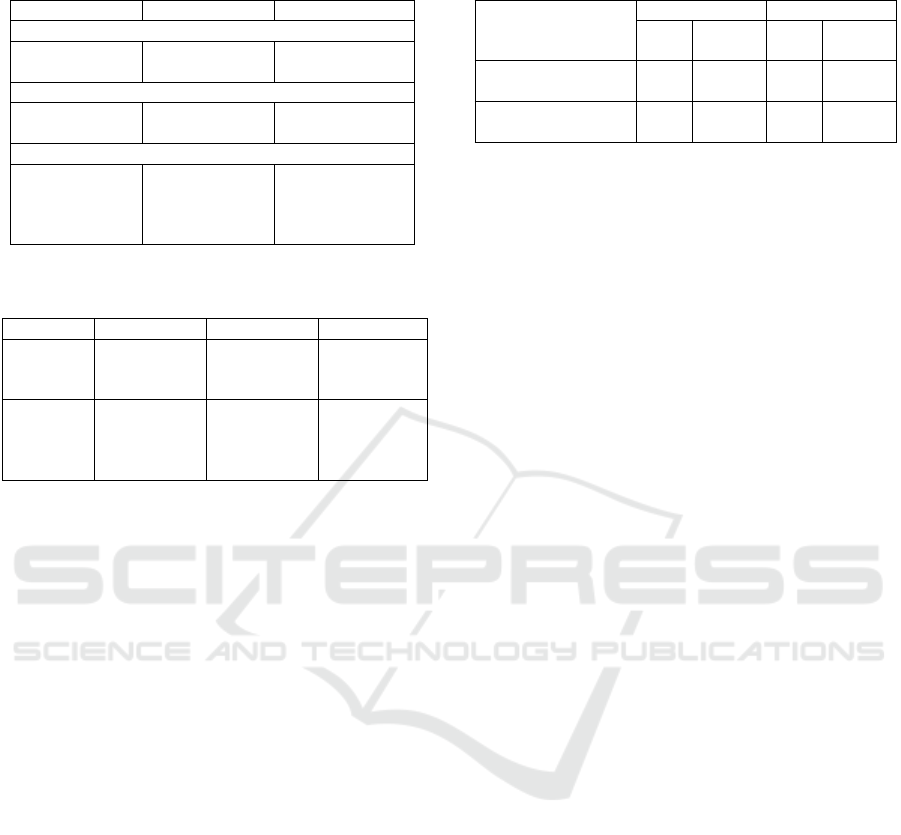
Table 3: System parameters and data sizes for Cayrel et al.
signature scheme over F
256
.
Parameter 80-bit Security 128-bit Security
Independent parameters:
n 144 230
δ 80 128
Derived parameters:
k 72 115
ω 54 87
Data size:
sk 1,152 bits 1,840 bits
pk 576 bits 920 bits
Signature 89.6 kB 229 kB
System param. 10.4 kB 26.5 kB
Table 4: Execution time and data sizes of the three signature
schemes for 128-bit security level.
Stern Jain et al. Cayrel et al.
Key-gen 0.0170 ms 0.0201 ms 0.339 ms
Sign 31.5 ms 16.5 ms 24.3 ms
Verify 2.27 ms 135 ms 9.81 ms
sk 1024 bit 1536 bit 1840 bit
pk 512 bit 512 bit 920 bit
(+ 65.5 kB)
∗
(+ 65.5 kB)
∗
(+ 229 kB)
∗
Signature 245 kB 263 kB 229 kB
∗
System parameters
Table 4. Eight variables of F
2
in the Stern and Jain
et al. signature schemes, and a variable of F
256
in
the Cayrel signature scheme are stored in an eight-
bit uint8 variable. Our implementation uses a pre-
computation table for multiplication between F
256
elements. We used SHA3-256 to implement random
oracles used in the signature schemes. For example, a
random oracle h : {0,1}
∗
→{0, 1}
1024
is implemented
as v 7→ SHA3-256(0x00kv)kSHA3-256(0x01kv)k
SHA3-256(0x02kv)kSHA3-256(0x03kv). One byte
prefix 0x00, 0x01, . . . , 0x03 are auxiliary inputs
to achieve independent hash functions. Durstenfeld
Shuffle (Durstenfeld, 1964) that outputs a random
permutation within O (n) computational complexity,
is used in the signature schemes.
The signature size in the Cayrel et al. signature
scheme is smaller and the execution time of the sig-
nature generation algorithm is smaller comparing to
the Stern signature scheme. Conversely, the signature
verification algorithm in the Stern signature scheme is
faster than that in the Cayrel et al. signature scheme
since it consists only of hash calculations, permuta-
tions, exclusive-or operations, and Hamming weight
checks. Table 4 show the execution time of the signa-
ture schemes on a PC with a 3.5 GHz CPU and 16 GB
of RAM and the size of the secret key, public key, and
a signature. The size of the input messages is 32 B.
Alaoui et al. (Alaoui et al., 2013), implemented
the signature schemes of Stern, Veron and Cayrel et
al. for 80 bits of security. Further, security of Veron’s
Table 5: Comparison between our Implementation and
(Alaoui et al., 2013).
Stern Cayrel et al.
Sign Verific. Sign Verific.
(ms) (ms) (ms) (ms)
Our Impliment. 31.5 2.27 24.3 9.81
(128 bits of sec.)
(Alaoui et al., 2013) 7.18 3.57 4.25 1.90
(80 bits of sec.)
scheme is fixed by Jain et al. We have implemented
the signature schemes of the Stern, Jain et al. and
Cayrel et al. for 128 bits of security. In table 5, we
have provided a comparison with the Stern and Cayrel
et al. schemes.
6 CONCLUSION
We derived code-based signature schemes using
Fiat-Shamir transformation on code-based zero-
knowledge identification schemes: the Stern scheme,
the Jain-Krenn-Pietrzak-Tentes scheme, and the
Cayrel-Veron-Alaoui scheme. We then analyzed the
security of the three signature schemes and derived
the security parameters to achieve the 128-bit level of
security. Furthermore, we implemented these signa-
ture schemes and compared their performance on a
PC. Our security analysis and implementation show
the Stern signature scheme is the most efficient re-
garding the size of the secret and public key and the
execution time of key generation and signature veri-
fication, and the Cayrel et al. scheme is the most su-
perior in terms of signature size. The signature ge-
neration of the Jain et al. scheme is the fastest, but
the signature verification of the scheme is slowest. In
our future work, we will optimize the implementation
for IoT devices and study techniques for reducing the
signature size.
REFERENCES
Alaoui, S. M. E. Y., Cayrel, P.-L., Bansarkhani, R. E., and
Hoffmann, G. (2013). Code-Based Identification and
Signature Schemes in Software. In CD-ARES Works-
hops 2013, pages 122–136.
Alaoui, S. M. E. Y., Dagdelen,
¨
O., V
´
eron, P., Galindo, D.,
and Cayrel, P.-L. (2012). Extended security arguments
for signature schemes. In International Conference on
Cryptology in Africa, pages 19–34. Springer.
Augot, D., Finiasz, M., and Sendrier, N. (2003). A Fast Pro-
vably Secure Cryptographic Hash Function. Crypto-
logy ePrint Archive, Report 2003/230. https://eprint.
iacr.org/2003/230.
Security Analysis and Efficient Implementation of Code-based Signature Schemes
219

Barg, S. (1994). Some new np-complete coding problems.
Problemy Peredachi Informatsii, 30(3):23–28.
Becker, A., Joux, A., May, A., and Meurer, A. (2012). De-
coding random binary linear codes in 2n/20: How 1+
1= 0 improves information set decoding. In Annual
International Conference on the Theory and Appli-
cations of Cryptographic Techniques, pages 520–536.
Springer.
Berlekamp, E., McEliece, R., and van Tilborg, H. (1978).
On the Inherent Intractability of Certain Coding Pro-
blems. IEEE Transactions on Information Theory,
24(3):384–386.
Cayrel, P.-L., Gaborit, P., and Prouff, E. (2008). Secure im-
plementation of the stern authentication and signature
schemes for low-resource devices. In International
Conference on Smart Card Research and Advanced
Applications, pages 191–205. Springer.
Cayrel, P.-L., V
´
eron, P., and Alaoui, S. M. E. Y. (2010).
A zero-knowledge identification scheme based on the
q-ary syndrome decoding problem. In International
Workshop on Selected Areas in Cryptography, pages
171–186. Springer.
Courtois, N. T., Finiasz, M., and Sendrier, N. (2001).
How to Achieve a McEliece-Based Digital Signature
Scheme. In Advances in Cryptology – ASIACRYPT
2001. ASIACRYPT 2001. Lecture Notes in Computer
Science, volume 2248, pages 157–174.
Dallot, L. (2008). Towards a Concrete Security Proof of
Courtois, Finiasz and Sendrier Signature Scheme. In
Research in Cryptology. WEWoRC 2007. Lecture No-
tes in Computer Science, volume 4945, pages 65–77.
Debris-Alazard, T., Sendrier, N., and Tillich, J.-P. (2017).
The problem with the SURF scheme. https://arxiv.org/
abs/1706.08065v4.
Durstenfeld, R. (1964). Algorithm 235: Random permuta-
tion. Commun. ACM, 7(7):420–.
Faug
´
ere, J.-C., Gauthier-Umana, V., Otmani, A., Perret, L.,
and Tillich, J.-P. (2011). A Distinguisher for High-
Rate McEliece Cryptosystems. In Information Theory
Workshop (ITW), IEEE, pages 282–286.
Finiasz, M. and Sendrier, N. (2009). Security Bounds for
the Design of Code-Based Cryptosystems. In Advan-
ces in Cryptology – ASIACRYPT 2009, volume 5912,
pages 88–105.
Gaborit, P. and Girault, M. (2007). Lightweight code-based
identification and signature. In Information Theory,
2007. ISIT 2007. IEEE International Symposium on,
pages 191–195. IEEE.
Jain, A., Krenn, S., Pietrzak, K., and Tentes, A. (2012).
Commitments and efficient zero-knowledge proofs
from learning parity with noise. In International Con-
ference on the Theory and Application of Cryptology
and Information Security, pages 663–680. Springer.
Kabatianskii, G., Krouk, E., and Smeets, B. (1997). A
Digital Signature Scheme Based on Random Error-
Correcting Codes. In Proceedings of the 6th IMA In-
ternational Conference on Cryptography and Coding.
May, A., Meurer, A., and Thomae, E. (2011). Decoding
random linear codes in
˜
O(2
0.054n
). In International
Conference on the Theory and Application of Crypto-
logy and Information Security, pages 107–124. Sprin-
ger.
Morozov, K., Roy, P. S., Steinwandt, R., and Xu, R. (2018).
On the security of the courtois-finiasz-sendrier signa-
ture. Open Mathematics, 16(1):161–167.
Niebuhr, R., Persichetti, E., Cayrel, P.-L., Bulygin, S., and
Buchmann, J. (2017). On lower bounds for informa-
tion set decoding over &fopf; q and on the effect of
partial knowledge. International journal of informa-
tion and Coding Theory, 4(1):47–78.
Otmani, A. and Tillich, J.-P. (2011). An Efficient Attack on
All Concrete KKS Proposals. In Post-Quantum Cryp-
tography. PQCrypto 2011. Lecture Notes in Computer
Science, volume 7071, pages 98–116.
Pointcheval, D. and Stern, J. (2000). Security Arguments
for Digital Signatures and Blind Signatures. Journal
of Cryptology, 13(3):361–396.
Shor, P. (1994). Polynomial-time algorithm for prime fac-
torization and discrete logarithms on a quantum com-
puter: proc. In 35th Annual Symp. on the Foundations
of Computer Science, volume 124.
Stern, J. (1988). A method for finding codewords of small
weight. In International Colloquium on Coding The-
ory and Applications, pages 106–113. Springer.
Stern, J. (1994). A new identification scheme based on
syndrome decoding. In Advances in Cryptology –
CRYPTO 1993. Lecture Notes in Computer Science,
volume 773, pages 13–21.
V
´
eron, P. (1997). Improved identification schemes based on
error-correcting codes. Applicable Algebra in Engi-
neering, Communication and Computing, 8(1):57–69.
ICISSP 2019 - 5th International Conference on Information Systems Security and Privacy
220