Optimum Stocks Portfolio Selection using Fuzzy Decision Theory

Liem Chin, Erwinna Chendra and Agus Sukmana

Department of Mathematics, Parahyangan Catholic University, Ciumbuleuit 94, Bandung, Indonesia

Keywords: Portfolio Selection, Fuzzy Decision Theory, Mixed-integer Linear Programming.

Abstract: An investor wants the value of his or her money does not have a decline in value against inflation. For this

reason, investors need to invest in financial instruments, one of which is stocks. Thus, investors need to

create an optimum stock portfolio. Generally, the factors considered by investors in creating an optimum

portfolio are expectations of return and portfolio risk. However, besides these two factors, the liquidity is

also an important factor to be considered. These three factors will be discussed in this paper to form an

optimum portfolio. In addition, because stock transactions use lot units, the optimization problem here is a

mixed-integer linear programming optimization problem that will be solved using the Branch and Bound

algorithm that is available in toolbox Matlab 2016. This optimization problem will be applied to the

formation of a portfolio consisting of stocks in LQ45 index. The LQ45 Stock Index was chosen because

shares in this index have high liquidity levels according to the Indonesia Stock Exchange. The

computation results show that the portfolio rebalancing model can form a portfolio based on the level of

satisfaction of investor.

1 INTRODUCTION

In 1952, Markowitz selected the optimum portfolio

by minimizing portfolio risk expressed by the

covariance matrix (Markowitz, 1952). However, this

is not efficient for large-scale portfolios because the

model proposed by Markowitz is quadratic

programming. Moreover, in this Markowitz model

only two factors are considered, namely return

expectations and portfolio risk.

Then, Fang et. al. developed this Markowitz

model by adding the liquidity factor to assets (Fang

et al., 2005). Liquidity is an important role in

investment. Liquidity is the level of possibility in

converting investments in cash without losing

significant value. Thus, this liquidity measures how

easily investors can buy and sell their assets. An

investor's portfolio is not good if it only has a high

return and low risk while the assets in the portfolio

are not liquid. If the assets in the portfolio are

illiquid, it means that investors will have difficulty

changing the assets in cash when investors need

money. Moreover, Fang et. al. do not measure

portfolio risk using the covariance matrix but rather

using semi-absolute deviation. By using this semi-

absolute deviation, the optimization problem

becomes a linear programming problem that can be

solved by the simplex method. Because risk is

measured by semi-absolute deviations, the problem

becomes simpler and more efficient for creating

large-scale portfolios. However, this model cannot

be directly used if the formed portfolio consists only

of shares because the purchase of shares must be in

lots. This lot unit is a nonnegative integer.

In our previous studies, we discussed portfolio

selection by considering the number of lots of shares

an investor needs to buy (Chin et al., 2018; Sukmana

et al., 2019). The model discussed is quite complex

because the objective function of the optimization

problem is non-linear function. For this reason, in

this study we will not measure portfolio risk using

covariance matrices but instead using semi-absolute

deviations as suggested by Fang et. al. In addition,

we will also use fuzzy decision theory to solve

portfolio optimization problems by considering the

lot units in stock purchases. Using this theory, the

optimization problem is a mixed-integer linear

programming problem because the objective

function is linear and there are constraints in the

form of non-negative integers. Then, with this fuzzy

decision theory, we will also make portfolio

rebalancing to maintain the target expected by

investors.

Chin, L., Chendra, E. and Sukmana, A.

Optimum Stocks Portfolio Selection using Fuzzy Decision Theory.

DOI: 10.5220/0010137400002775

In Proceedings of the 1st International MIPAnet Conference on Science and Mathematics (IMC-SciMath 2019), pages 125-131

ISBN: 978-989-758-556-2

125

The developed model will be applied to create an

optimum portfolio where this portfolio consists only

of stocks listed in the LQ45 index. The LQ45 stock

index was first launched in February 1997. This

index is one of the benchmark indexes in the

Indonesian capital market. The Indonesia Stock

Exchange prescribe the principle of LQ45 index and

it consist of 45 shares. The criteria include liquidity

and market capitalization. In the regular market, the

liquidity is mainly measured by the transaction

value. However, since January 2005 the authority of

capital market in Indonesia added the transaction

frequency and the number of trading days as a

measure of liquidity (Indonesia Stock Exchange

(ISE), 2010). Stocks that are included in the LQ45

index calculation will be evaluated every three

months and the replacement of stocks in the LQ45

index is completed every six months, namely in

early February and August.

To solve the optimization problem in this study,

we will use the Branch and Bound method (Chen et

al., 2010). Then, this method will be implemented

with software Matlab. We will use five years the

shares price data, that is 1 July 2014 to 30 June 2019

(Yahoo Finance, 2019).

2 DISCUSSION OF THE MODEL

Assume that there are 𝑛 assets in a portfolio and 𝑟



represents the percentage return rate from the asset-𝑖

in the 𝑗-th period with 𝑖1,2,…,𝑛 and 𝑗

1,2,…,𝑇 and suppose that 𝑚𝑛. Moreover, let

𝑦





𝑖1,2,…,𝑛



represents the proportion of the

amount of investment for the asset-𝑖. The semi-

absolute deviation of return on the portfolio under

the expected return over the past period 𝑗, 𝑗

1,⋯ ,𝑇 given as

𝑣





𝒚



min0,𝑟



𝑟



𝑦













∑

𝑟



𝑟



𝑦









∑

𝑟



𝑟



𝑦







(1)

with 𝑦



𝑦



,𝑦



,⋯,𝑦







. If 𝑟



denote expected rate

of return of asset 𝑖, the portfolio risk (𝑉) can be

determined as (Fang et al., 2005)

𝑉



𝒚





𝑇

𝑣





𝑦













∑

𝑟



𝑟



𝑦









∑

𝑟



𝑟



𝑦







2𝑇







(2)

A fuzzy number 𝐹 is called trapezoidal with

tolerance interval



𝑎,𝑏



, left width 𝛼 and right width

𝛽 if its membership function takes the following

form

𝐹



𝑣





⎩

⎪

⎨

⎪

⎧

1

𝑎𝑣

𝛼

1

𝑣𝑏

𝛽

,if 𝑎𝛼𝑣a

,if 𝑎𝑣𝑏

,if 𝑎𝑣𝑏𝛽

otherwise

(3)

and we denote 𝐹 as 𝐹



𝑎,𝑏,𝛼,𝛽



. In this study,

the turnover rate of the stocks 𝑖 is defined by the

trapezoidal fuzzy number 𝑙









𝑙𝑎



,𝑙𝑏



,𝛼



,𝛽





. So,

the turnover rate of the portfolio 𝑦 is

∑

𝑙





𝑦







. The

crisp possibilistic mean value of the turnover rate of

the portfolio 𝑦 is represented by (Fang et al., 2005)

𝐸



𝑙





𝒚





𝐸𝑙





𝑦







𝐸𝑙





𝑦











𝑙𝑎



𝑙𝑏





𝛽



𝛼











𝑦



(4)

The equation (4) is used to measure the portfolio

liquidity.

To accommodate the investor’s desire, the 𝑆

shape membership function is used to proclaim the

aim of investment of an investor. The 𝑆 shape

membership function itself is given by

𝑓



𝑣





1ex



𝜏𝑣



(5)

With equation (5), the membership function for

expected return, risk and liquidity are given as

follows:

1) Membership function for expected return of

portfolio

𝜇





𝒚





1exp



𝛼



𝐸𝑟



𝒚



𝑟







(6)

with 𝛼



is investor’s satisfaction level about the

expected return and 𝑟



is the mid-point where

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

126

the membership function value is 0.5. This 𝑟



be regarded as the middle goal level for the

portfolio return.

2) Membership function for portfolio risk

𝜇





𝒚





1exp



𝛼





𝑤



𝒚



𝑤







(7)

With 𝛼



is the investor’s satisfaction level about

the risk portfolio and 𝑤



is the mid-point where

the membership function value is 0.5. This 𝑤



be regarded as the middle goal level for the

portfolio risk.

3) Membership function for portfolio liquidity

𝜇





𝒚





1exp



𝛼





𝐸



𝑙





𝒚





𝑙







(8)

With 𝛼



is the investor’s satisfaction level about

the liquidity and 𝑙



is the mid-point where the

membership function value is 0.5. This 𝑙



regarded as the middle goal level for the

portfolio liquidity.

Using the semi-absolute deviation, trapezoidal

fuzzy number and the 𝑆 shape membership function,

the model of selection portfolio is given as (Fang et

al., 2005)

max𝜃

(9)

subject to

𝛼



𝑟



𝑦







𝑝



𝑦





𝑦











𝜃

𝛼



𝑟



(10)

𝜃

𝛼



𝑇

𝑢







𝛼



𝑤



(11)

𝛼





𝑙𝑎



𝑙𝑏





𝛽



𝛼









𝑦



𝜃𝛼



𝑙



(12)

𝑢



𝑟



𝑟



𝑦







0,

𝑗

1,2,⋯,𝑇

(13)





𝑦





𝑦





𝑦











𝑝



𝑦





𝑦











1

(14)

𝑦



𝑦





𝑦





𝑦





,𝑖1,2,⋯,𝑛

(15)

0𝑦





𝑤



,𝑖1,2,⋯,𝑛

(16)

0𝑦





𝑦





,𝑖1,2,⋯,𝑛

(17)

𝑢



0,

𝑗

1,2,⋯,𝑇

(18)

𝜃0

(19)

where

𝑝 is the rate of transaction cost;

𝑦





is the proportion of the amount of investment for

the asset-𝑖 before portfolio rebalancing;

𝑦





,𝑦





are the proportion of the amount of

investment for an asset-𝑖 bought and sold by the

investor, respectively;

𝑤



is upper bound of the proportion of the amount of

investment to buy an asset-𝑖;

𝑙𝑎



,𝑙𝑏



,𝛽



,𝛼



is trapezoidal fuzzy number.

The problem (9) with constraints (10)-(19) is a linear

programming problem. This problem can be solved

using the simplex method, for an instance. If the

investor has not the portfolio yet, the 𝑦





’s is set to

zero so we only get the 𝑦





’s. It is clear because the

short selling is not allowed to form the portfolio.

Besides short selling is not allowed, stocks are

traded in lots in regular market in Indonesia Stock

Exchange, which 1 lot equal to 100 shares. So, if 𝑧



is the number of lots of shares traded, we have the

relationship between 𝑧



and 𝑦



as follow

𝑦



100

𝑧



𝑃



𝑀

(20)

where

𝑃



is price of stock 𝑖 and 𝑀 is an investor’s capital.

In similar way, we have the relation between

𝑦





,𝑦





,𝑦





and 𝑧





,𝑧





,𝑧





respectively as follow

𝑦





100

𝑧





𝑃





𝑀

(21)

𝑦





100

𝑧





𝑃





𝑀

(22)

𝑦





100

𝑧





𝑃





𝑀

(23)

where

𝑧





is the number of lots for the stock-𝑖 before

portfolio rebalancing;

𝑧





,𝑧





are the number of lots for the stock-𝑖 bought

and sold by the investor, respectively;

𝑃





is the price of stock 𝑖 before rebalancing;

𝑃





,𝑃





are the price of stock 𝑖 bought and sold by

the investor, respectively.

Next, substitute equation (20)-(23) to equation (15)

𝑧





𝑧





𝑃





𝑧





𝑃





𝑧





𝑃





𝑃



(24)

If the investor has not the portfolio yet, the 𝑧





’s is

set to zero so we only get the 𝑧





’s (because short

selling is not allowed). If the investor wants to

rebalance his portfolio, then we assume that the

Optimum Stocks Portfolio Selection using Fuzzy Decision Theory

127

purchase and selling price of stock is same, that is

𝑃





𝑃





𝑃



Finally, we can get the model for selection

portfolio with decision variable is a number of lots

for stock to buy or sell, that is

max𝜃

(25)

subject to

100

𝑀

𝛼



𝑟



𝑧



𝑃







𝑝



𝑧





𝑃





𝑧





𝑃













𝜃𝛼



𝑟



(26)

𝜃

𝛼



𝑇

𝑢







𝛼



𝑤



(27)

100

𝑀

𝛼





𝑙𝑎



𝑙𝑏





𝛽



𝛼









𝑧



𝑃



𝜃

𝛼



𝑙



(28)

𝑢





100

𝑀

𝑟



𝑟



𝑧



𝑃







0,

𝑗

1,2,⋯,𝑇

(29)

100

𝑀





𝑧





𝑃





𝑧





𝑃





𝑧





𝑃











𝑝



𝑧





𝑃





𝑧





𝑃











1

(30)

𝑧





𝑧





𝑃





𝑧





𝑃





𝑧





𝑃





𝑃



𝑖1,2,⋯,𝑛

(31)

0𝑧







𝑤



𝑀

100𝑃





,𝑖1,2,⋯,𝑛

(32)

0𝑧







𝑧





𝑃





𝑃





,𝑖1,2,⋯,𝑛

(33)

𝑢



0,

𝑗

1,2,⋯,𝑇

(34)

𝜃0

(35)

Actually, equation (31) is no longer needed because

we can substitute that to equation (26), (28) and

(29). Therefore, there are only nine constraints for

the model. The 𝑧





’s and 𝑧





‘s are non-negative

integer because they are number of lots for the

stock-𝑖 bought and sold by the investor. So, the

objective function in (25) with its constraints (26)-

(35) is a mixed-integer linear programming problem

rather than a linear programming problem. Here is

the complete model

max𝜃

(36)

subject to

100

𝑀

𝛼



𝑟



𝑧



𝑃







𝑝



𝑧





𝑃





𝑧





𝑃













𝜃𝛼



𝑟



(37)

𝜃

𝛼



𝑇

𝑢







𝛼



𝑤



(38)

100

𝑀

𝛼





𝑙𝑎



𝑙𝑏





𝛽



𝛼









𝑧



𝑃



𝜃

𝛼



𝑙



(39)

𝑢





100

𝑀

𝑟



𝑟



𝑧



𝑃







0,

𝑗

1,2,⋯,𝑇

(40)

100

𝑀





𝑧





𝑃





𝑧





𝑃





𝑧





𝑃











𝑝



𝑧





𝑃





𝑧





𝑃











1

(41)

0𝑧







𝑤



𝑀

100𝑃





,𝑖1,2,⋯,𝑛

(42)

0𝑧







𝑧





𝑃





𝑃





,𝑖1,2,⋯,𝑛

(43)

𝑢



0,

𝑗

1,2,⋯,𝑇

(44)

𝜃0

(45)

𝑧





,𝑧





∈ℤ



(46)

where 𝑧



is given by equation (24) and 𝑍



represent

non-negative integer. The optimization problem

above is solved using branch and bound algorithm.

This algorithm is available in Matlab 2016 which

syntax is intlinprog.

3 RESULTS

In this section, we give a numerical example to

illustrate the proposed portfolio rebalancing model.

There are 45 stocks in LQ45 index. We neglect six

stocks because five among of them have a negative

expected return rate and one stock just offered the

shares in 2016 through an initial public offering

(IPO). So, we use 39 stocks in total and collect

historical data from 1 July 2014 to 30 June 2019.

The data are downloaded from the web-site

www.finance.yahoo.com. Then, we use one month

as a period to obtain the historical return rate for 60

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

128

periods. Assume that the rate of transaction costs

for purchase and sell stock is 0.002.

Next, we give an example of the estimation

method for the fuzzy turnover rates for TLKM (PT

Telekomunikasi Indonesia Tbk.). Since the future

turnover rates of the stocks is assumed trapezoidal

fuzzy numbers, so tolerance interval, left width and

right width need to estimate. These parameters are

estimated using frequency statistic method. In this

study, we used the historical data of the stocks

turnover rates. First, the frequency of historical

turnover rates is calculated via daily turnover rates

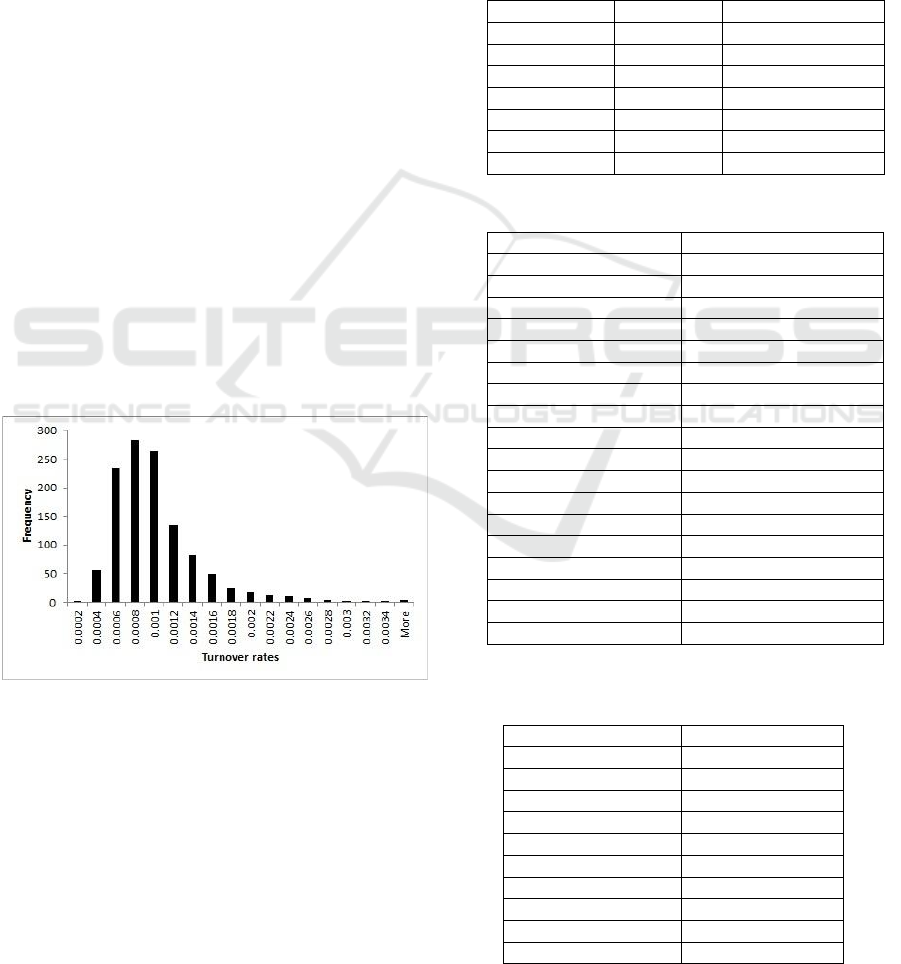
from 1 July 2014 to 30 June 2019. Figure 1

expresses the frequency distribution of historical

turnover rates for stock TLKM. Consider that the

most of the historical turnover rates fall into the

intervals



0.0004,0.0006





0.0006,0.0008





0.0008,0.0010



and



0.0010,0.0012



. We regard

that the left and right endpoints of the tolerance

interval, respectively, as the mid-points of the

intervals



0.0004,0.0006



and



0.0010,0.0012



So, the tolerance interval of the fuzzy turnover rate



0.0005,0.0011



. By observing all the historical

data, the minimum and the maximum possible

values of uncertain turnover rates in the future are

0.00014 and 0.00383, respectively. Assume that

the rate of transaction costs for purchase and sell

stock is 0.002.

Therefore, the left width is 0.00036 and the right

width is 0.002733.

Figure 1: Frequency of turnover rates of TLKM.

Thus, the fuzzy turnover rate of stock TLKM is



0.0005,0.0011,0.00036,0.002733



In general, there are two kinds of investor, i.e.

conservative and aggressive. So, in the following,

we give two kinds of computational results. For

conservative investor, the value of 𝑟



,𝑤



and 𝑙



given by 0.02,0.024 and 0.016 whereas for

aggressive investor, the value of 𝑟



,𝑤



and 𝑙



given by 0.05,0.06 and 0.04. For each case, we

propose two portfolios. The one, investor has not a

portfolio yet (so 𝑧





0 for all 𝑖) and the other,

investor has already a portfolio contain of seven

stocks with the number of lots as shown in Table 1.

Stock’s prices for portfolio rebalancing lots are

shown in Table 2 (prices appear only for stocks that

are bought or sold to rebalance the portfolios in

Table 3-6). For all cases, the value of 𝛼



,𝛼



and 𝛼



are given by 600,800 and 600, respectively. The

investor’s fund to form portfolios Table 3 and Table

4 is Rp 100,000,000.

Table 1: Number of lots of stocks.

Stoc

Lots Stock’s Price

(

AKRA 75 4,000

BBCA 10 29,400

HMSP 50 3,360

JSMR 60 5,700

PTBA 100 2,940

TLKM 20 4,040

UNVR 20 44,650

Table 2: Stock’s price for portfolio rebalancing.

Stoc

Stock’s Price (Rp)

AKRA 4,090

ANTM 845

BBCA 29,975

BBTN 2,460

BRPT 3,210

ELSA 378

ERAA 1,920

HMSP 3,140

INDY 1,680

INKP 9,375

JSMR 5,725

PTBA 2,960

PWON 730

SRIL 338

TKIM 12,575

TLKM 4,140

TPIA 4,970

UNVR 45,000

Table 3: Portfolio rebalancing lots with 𝑟



0.02,𝑤





0.024,𝑙



0.016 and 𝑧





0 for all 𝑖.

Stoc

Buy

AKRA 1

ANTM 1

BBTN 1

BRPT 35

ELSA 607

ERAA 51

INDY 30

PWON 213

SRIL 739

TLKM 23

Optimum Stocks Portfolio Selection using Fuzzy Decision Theory

129

Table 4: Portfolio rebalancing lots with 𝑟



0.05,𝑤





0.06,𝑙



0.04 and 𝑧





0 for all 𝑖.

Stoc

BRPT 40

ELSA 320

ERAA 122

HMSP 1

INDY 148

SRIL 739

Table 5: Portfolio rebalancing lots with 𝑟



0.02,𝑤





0.024,𝑙



0.016 and contain seven stocks as in Table 1.

Stoc

BR Buy Sell AR

AKRA 75 0 72 3

BBCA 10 0 10 0

BBTN 0 2 0 2

BRPT 0 100 0 100

ELSA 0 1378 0 1378

ERAA 0 126 0 126

HMSP 50 0 50 0

INDY 0 68 0 68

JSMR 60 0 60 0

PTBA 100 0 100 0

PWON 0 535 0 535

SRIL 0 1754 0 1754

TLKM 20 23 0 43

UNVR 20 0 20 0

Table 6: Portfolio rebalancing lots with 𝑟



0.05,𝑤





0.06,𝑙



0.04 and contain seven stocks as in Table 1.

Stoc

BR Bu

Sell AR

AKRA 75 0 75 0

BBCA 10 0 10 0

BBTN 0 1 0 1

BRPT 0 120 0 120

ELSA 0 589 0 589

ERAA 0 303 0 303

HMSP 50 0 50 0

INDY 0 352 0 352

JSMR 60 0 60 0

PTBA 100 0 100 0

SRIL 0 1754 0 1754

TLKM 20 0 20 0

UNVR 20 0 20 0

BR and AR in Table 5 and Table 6 refer to

number of lots of stocks before and after portfolio

rebalancing, respectively. From Table 3-6, it can be

seen that the portfolios owned by a conservative

investor (Table 3 and Table 5) are more numerous of

stocks than those of an aggressive investor (Table 4

and Table 6). On Table 3, it can be seen that almost

a half of investor’s fund is invested to buy SRIL and

ELSA whereas on Table 4, that fund is invested to

buy SRIL and ERAA.

If we assume that an investor already has the

portfolio in Table 1, then the investor’s fund is Rp

237.18 million. The results are slightly different

from the previous portfolios. Almost a half of

investor’s fund is invested to buy SRIL and ELSA

for a conservative investor (Table 5) and that fund is

invested to buy SRIL and INDY (Table 6).

4 CONCLUSIONS

Liquidity factor plays an important role besides

expected return and risk. Liquidity is measured

using the turnover rates of stocks. The levels of

investor’s goals are appraised to be fuzzy numbers

with a non-linear S shape membership function.

These goals are expected return, risk and liquidity.

Considering all these factors together with fuzzy

decision theory, transaction costs and a number of

lots for stocks as the decision variable, a mixed-

integer linear programming model for portfolio

rebalancing is proposed. The computation results

show that the portfolio rebalancing model can form

a portfolio based on the level of satisfaction of

investor.

ACKNOWLEDGEMENTS

This research is supported by Lembaga Penelitian

dan Pengabdian kepada Masyarakat (LPPM)

Parahyangan Catholic University.

REFERENCES

Chen, D. S., Batson, R. G., & Dang, Y. (2010). Applied

integer programming: modeling and solution. John

Wiley & Sons, Inc.

Chin, L., Chendra, E., & Sukmana, A. (2018). Analysis of

portfolio optimization with lot of stocks amount

constraint: case study index LQ45. IOP Conf. Series:

Materials Science and Engineering, 300.

Fang, Y., Lai, K. K., & Wang, S. Y. (2005). Portfolio

rebalancing model with transaction costs based on

fuzzy decision theory. European Journal of

Operational Research, 175(2), 879–893.

Indonesia Stock Exchange (ISE). (2010). Buku panduan

indeks harga saham Bursa Efek Indonesia.

https://idx.co.id/media/1481/buku-panduan-indeks-

2010.pdf

Markowitz, H. (1952). Portfolio Selection. The Journal of

Finance, 7(1), 91.

Sukmana, A., Chin, L., & Chendra, E. (2019). Analysis of

IMC-SciMath 2019 - The International MIPAnet Conference on Science and Mathematics (IMC-SciMath)

130

portfolio optimization with inequality constraints. IOP

Conf. Series: Journal of Physics, 1218.

Yahoo Finance. (2019). No Title.

Www.Finance.Yahoo.Com. 5 July 2019

Optimum Stocks Portfolio Selection using Fuzzy Decision Theory

131