Measuring Construct Validity and Students’ Mathematical Creative
Thinking Skills
Kadir
1
and Irna Rahmawati
1
1
Department of Mathematics Education, Universitas Islam Negeri Syarif Hidayatullah Jakarta
Keywords: Construct validity, mathematical creative thinking skills, confirmatory factor analysis.
Abstract: This study aims to measure construct validity tests of mathematical creative thinking skills (MCTS) and
analyze students' MCTS. This research was conducted at a Junior High Schools in the city of Bekasi. This
study was a survey involving 180 students as participants. Data analysis uses confirmatory factor analysis
(CFA) and path analysis. The results revealed that: (1) Tests of MCTS are valid and consistently measured
through fluency, elaboration, flexibility, and originality constructs; (2) Construct reliability of the fluency
indicator is 0.952, elaboration of 0.976, flexibility of 0.622, and originality of 0.710; (3) Overall the average
student's MCTS is 50.27 on a scale (0-100), where female students are 61.45 and male is 49.54.
Achievement the highest MCTS of students is obtained in the flexibility indicator of 68.08 then the fluency
is 66.95, elaboration is 34.30, and the lowest is the originality indicator 31.76; (4) Students' MCTS on the
fluency indicator has an indirect effect on the indicator of originality through moderating indicators of
elaboration and flexibility. The conclusion of this study is that MCTS are measured from indicators of
fluency, elaboration, flexibility, and originality. The overall MCTS of students is still relatively low, where
female students are quite good and higher than male students. The ability to solve problems in the
originality indicator is the core of MCTS.
1 INTRODUCTION
The intellectual factor needed to develop
competitiveness in the industrial revolution era 4.0 is
the ability to think creatively. It is included in the
category of high-level thinking skills (HOTs).
Educational institutions are the most conducive
place to develop curricula that can produce creative
and competitive graduates. (Saini, 2015), argued that
the development of the 2013 curriculum, strives to
improve the quality of education to produce
graduates who are creative and able to face future
challenges. The development and formation of
individual creativity potential must be integrated in
the curriculum content. Furthermore, (Sternbergn,
2001) and (Sternbergn & Lubart, 2000) suggested
that individual creative potential will be latent if not
developed and formed.
Mathematics as part of the curriculum plays an
important role in fostering students to have creative
thinking skills. It is a way or method of thinking and
is taught to build the mindset. Moreover, reasoning
of students in solving problems critically, logically
and precisely.
The vision of learning mathematics are: (1)
directing understanding of mathematical concepts
and ideas needed to solve mathematical and other
scientific problems, (2) providing opportunities for
developing logical, systematic, critical and careful,
creative reasoning abilities , fostering self-
confidence, and a sense of beauty towards the nature
of mathematics (Hendriana & Sumarmo, 2014).
Mathematical creativity is defined as a
framework of mathematical knowledge is the ability
to solve problems or to develop thinking in a
structure, taking into account the logic-deductive
nature that is typical of the discipline, and the
concepts produced. Because the definition is related
to originality and usability, the definition of
mathematics (Kadir, Lucyana, & Satriawati, 2017).
Mathematical creativity at a professional level,
defined as: 1) The ability to produce original works
that significantly expand the body of knowledge; 2)
The ability to open new questions for other
mathematicians; 3) Processes that produce unusual
and profound solutions to given problems or analog
problems; 4) Formulation of questions and / or new
Kadir, . and Rahmawati, I.
Measuring Construct Validity and Students’ Mathematical Creative Thinking Skills.
DOI: 10.5220/0009914406670674
In Proceedings of the 1st International Conference on Recent Innovations (ICRI 2018), pages 667-674
ISBN: 978-989-758-458-9
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
667

possibilities that allow old problems to be
considered from a new perspective (Sriraman, 2005)
Creative thinking includes aspects of cognitive,
affective, and metacognitive skills. The aspect of
cognitive skills contains the ability: identify
problems, compose different questions, identify
relevant and irrelevant data, generate many ideas
(fluency), different ideas (flexibility), new ideas,
change old mindsets and habits, compose new
relationships and renew plans or ideas (Siswono,
2008). The characteristics of creative thinking
abilities, includes: 1) Fluency, namely the ability to
produce many ideas, solve problems or questions; 2)
Flexibility, namely the ability to produce many
varied and different ways; 3) Originality, namely the
ability to think in new ways or with unique
expressions and unusual thoughts from thoughts that
are clearly known; 4) Elaboration, namely the ability
to detail an object, idea, or situation (Siswono,
2008). Based on this definition, it can be concluded
that the ability to think creatively in mathematics
learning which later became known as mathematical
creative thinking skills (MCTS) is an ability that
reflects fluency, flexibility, and originality in
thinking, as well as the ability to elaborate an idea in
solving mathematical problems. Thus, the indicator
of MCTS are fluency, elaboration, flexibility, and
originality.
But in reality, MCTS Indonesian students have
not been reached maximally. The results of an
international study of the 2015, Program for
International Student Assessment (PISA) showed
that only about 10% of Indonesian students were
able to answer level 4, 5, and 6 tests. Characteristics
of tests at level 4, 5, and 6, contained questions
which requires the ability to construct, express
explanations and compile arguments based on
interpretation. Work in complex situations, identify
constraints, choose, compare, and evaluate problem
solving strategies, use broad reasoning, reflect,
formulate and express interpretations and reasoning.
Think of high-level mathematics and put it right
about their findings, arguments, and accuracy in the
original situation (PISA, 2015). Furthermore, the
results of Fardah's research revealed that the
achievement of MCTS of elementary and secondary
school students is still in the low category, which is
46.67% (Fardah, 2012).
Some of the efforts to improve students’ MCTS,
are in providing learning interventions through work
on non-routine problem tests. Learning evaluations
that involve students in completing non-routine tests
must be presented in class. According to Novita et
al., (Novita, Zulkardi, & Hartono, 2012) that one of
the factors causing low scores obtained by students
on the PISA test is the test material and international
standardized test from PISA not yet taught in class.
Besides that most tests in the evaluation process are
still at a low level. Therefore, the mathematical
problem solving test formulated in PISA can be
adapted to develop MCTS tests.
Several recent studies in Indonesia are related to
the development of students’ MCTS instruments
(Fitriani & Yarmayani, 2018) (Fitriani &
Yarmayani, 2018) (Fitriarosah, 2016) (Moma,
2015). Generally this research is a development
research with validity analysis, reliability,
discriminating index, and item difficulty level. The
study has not developed and measured the construct
through the Confirmatory Factor Analysis
procedure. Almost no research has specifically
explained the theoretical constructs of the MCTS
test empirically. Therefore, this study aims to: (1)
measure the construct validity of MCTS tests, and
(2) analyze students' MCTS.
2 METHOD
This study was a survey conducted in 6 junior high
schools (SMP A, SMP B, SMP C, SMP D, SMP E
and SMP F) in the city of Bekasi involving 180
students (male = 98, female = 82) as participants. A
total of 30 students were taken randomly from each
school. The MCTS test developed in the form of an
essay consists of 11 items, representing fluency
indicators, elaboration, flexibility, and originality.
Representation of items into indicators, including:
fluency (1, 2, 3), elaboration (4, 5), flexibility (6, 7,
8), and originality (9, 10, 11). This study involves
rectangular flat geometry. Before empirically testing
MCTS test items, it was first assessed the feasibility
of expert panelists from the aspect of content and the
accuracy of items measuring indicators.
Furthermore, an assessment of student answers from
the MCTS test results uses a rubric adapted from
Bosch (Bosch, 2008). The rubrics of students'
creative mathematical thinking skills, in Table 1.
Table 1: Rubric of the MCTS Test
Indicator
Score
Descriptors
Fluency
0
No answer or no relevant
answer
1
Give an idea that is relevant to
problem solving but the
disclosure is less clear or
wrong.
2
Provide an idea that is relevant
to problem solving but the
ICRI 2018 - International Conference Recent Innovation
668

completion and disclosure is
incomplete or unclear.
3
Provide more than one
idea/answer that is relevant to
solving the problem but the
solution is unclear.
4
Provide more than one
idea/answer that is relevant to
problem solving and full and
clear disclosure.
Elaboration
0
Don't answer or give the wrong
answer.
1
There is a mistake in expanding
the situation without details.
2
There is a mistake in expanding
the situation and still not
detailed.
3
Extending the situation
correctly but not detailed.
4
Expand the situation correctly
and in detail.
Flexibility
0
Do not answer or give answers
in one way or more but
everything is wrong.
1
Give answers in only one way,
there are errors in the
calculation process, that the
results are wrong.
2
Give answers in one way, the
calculation process and the
results are correct.
3
Give answers in more than one
way (various) but the results are
wrong because there is a
mistake in the calculation
process.
4
Give answers in more than one
way (various), the calculation
process of the results is correct.
Originality
0
Do not give answers or give
wrong answers.
1
Give answers in their own way
but cannot be understood.
2
Providing an answer in its own
way, the calculation process is
directed but not completed.
3
Give answers in their own way
but the results are wrong
because there is a mistake in the
calculation process.
4
Give answers in their own way,
the calculation process and the
results are correct.
The data analysis technique uses Confirmatory
Factor Analysis (CFA) with Lisrel 88.00 and AMOS
version 20. CFA analysis techniques use SEM
(Structural Equation Modeling) with a measurement
model. Item validity is determined based on the
loading factor test. Empirically an indicator or item
is said to be valid measuring construct if the
estimation results of loading factor () > 0.5 or has a
t-test statistical value with a p-value < 0.05.
An indicator is said to be dominant if it has 
2
≥
0.70 (Hair, Black, Babin, & Anderson, 2010).
Determination of Composite Reliability is based on
a composite internal consistency of construct
measurement indicators. In general a construct,
unidimensional, precise, and consistent can be
measured by indicators / items, if: (a) the model is fit
with the data, (b) Loading factor () is significant
above 1.96 or () > 0.50 and (c) Estimation of the
coefficient of CR (Composite Reliability) ≥ 0.70 and
VE (Variance Extracted) ≥ 0.50 (Hair et al., 2010).
The Construct Reliability (CR) and Variance
Extracted (VE) formulas are as follows:
,=and=
2
1
1
2
1
2
1
k
VECR
k
i
i
i
k
i
i
k
i
i
k
i
i
i


































w
here:
i

= loading indicator factor to - i,
i

= indicator variance error to – i
k
= number of indicators in the model
3 RESULTS AND DISCUSSION
CFA analysis technique aims to estimate the
accuracy of the items that measure factors that have
been compiled based on theoretical constructs.
Through CFA analysis, the construct estimates are:
(1) fluency, (2) elaboration, (3) flexibility, and (4)
originality.
3.1 Construct Validity
The results of estimation of loading factor in Table
2.
Table 2: Results of estimated loading factor with CFA
Factors
No
Loading
Factor
t
observe
t
table
Decisi
on
Fluency
1
0.986
18.408
1.96
Sig
2
0.961
17.409
1.96
Sig
3
0.978
18.135
1.96
Sig
Elaboratio
n
4
0.986
17.571
1.96
Sig
5
0.990
17.681
1.96
Sig
Flexibility
6
0.277
2.108
1.96
Sig
7
0.359
2.270
1.96
Sig
8
0.065
0.576
1.96
Non
Sig
Originalit
y
9
0.713
7.527
1.96
Sig
10
0.319
3.616
1.96
Sig
11
0.473
5.449
1.96
Sig
Measuring Construct Validity and Students’ Mathematical Creative Thinking Skills
669

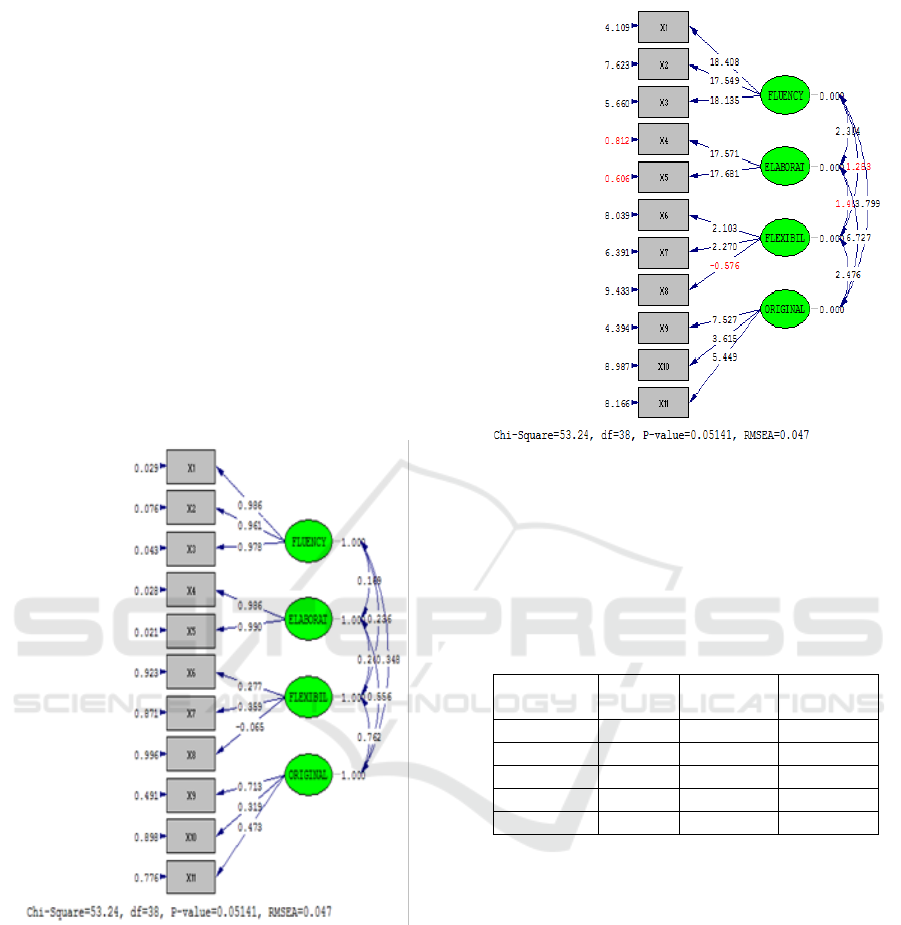
Based on the results of the analysis in Table 2, it
shows that all items except item number 8, have t-
observe > t-table = 1.96. This means that all items of
MCTS except item number 8 are declared valid
measuring constructs of fluency, elaboration,
flexibility, and originality. Thus, the MCTS
consisted of 10 items (valid) and four indicators,
namely fluency consisting of 3 items with loading
factors (0.986; 0.961; 0.978), elaboration consisting
of 2 items with loading factors (0.986; 0.990),
flexibility consisting of 2 items with loading factors
(0.277; 0.359) and originality consisted of 3 items
with loading factors (0.713; 0.319; 0.473). The
findings of this study, in contrast to the findings of
(Fitriarosah, 2016) about the MCTS, found a set of
MCTS test consisting of 4 valid items, the reliability
of good categories, also had a good discriminating
index and varying degrees of difficulty.
Visually loading factors from the MCTS test are
presented in the path diagram in Figure 1.
Figure 1: Path Diagram of Loading Factor
The path diagram of the factor loading estimation
results from the MCTS test with the t-test is
presented in Figure 2.
Figure 2: Path Diagram of the Loading Factor with the t-
test
3.2 Reliability
The reliability estimation results from the MCTS test
are presented in Table 3.
Table 3: Results of MCTS test reliability estimates
Factor
Number
of items
Construct
Reliability
Varians
Extracted
Fluency
3
0.952
0.952
Elaboration
2
0.976
0.976
Flexibility
2
0.622
0.503
Originality
2
0.710
0.578
Total
10
0.815
0.752
From the results of the analysis in Table 3, the
overall CR value is 0.815 and VE is 0.752. By using
criteria from estimates for CR ≥ 0.70 and VE ≥
0.50, this finding reveals that the construct of the
test, right, and consistently measuring MCTS or
having internal consistency is good (Hair et al.,
2010). This finding is similar to La Moma's finding
that the MCTS test reliability is 0.840 but uses the
Cronbach Alpha formula (Moma, 2015).
3.3 Test of Goodness of Fit Statistics
Testing fit models aimed at studying how precise the
measurement model proposed can fit the research
data. The results of the analysis relating to the size
of the model Fit, are presented in Table 4.
ICRI 2018 - International Conference Recent Innovation
670

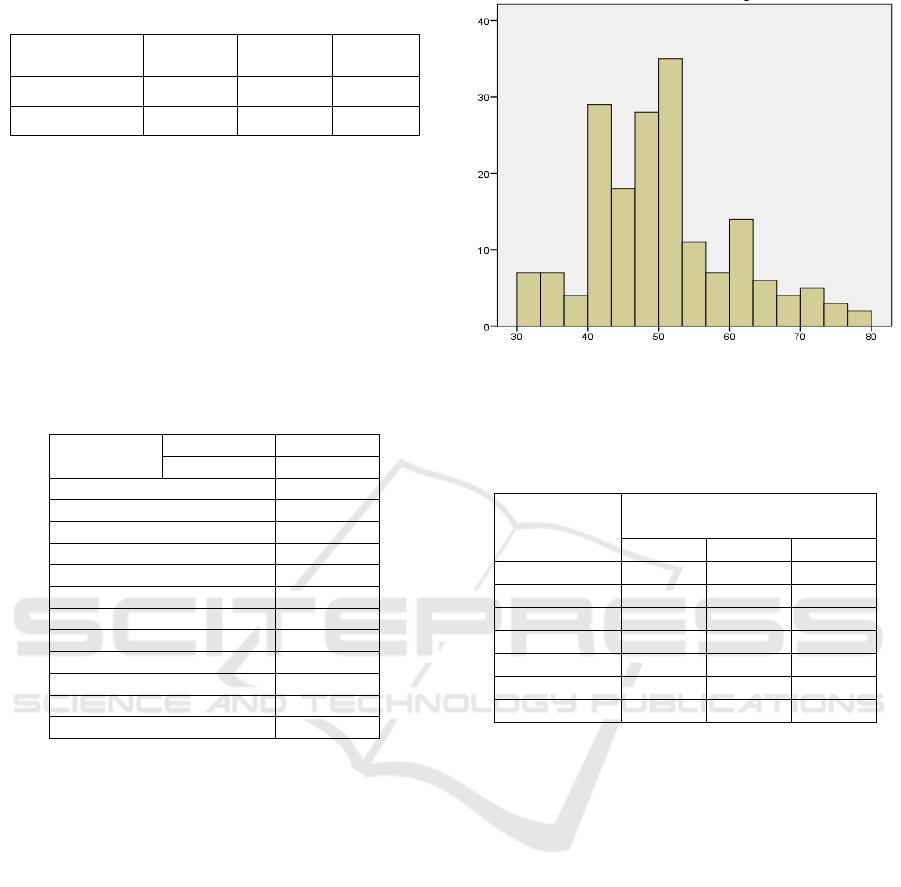
Table 4: Summary of fit model indication
Goodness of
Fit
Fit
Indicators
Result
Judge
Chi-Square (p)
p > 0.05
p = 0.051
fulfilled
RMSEA
< 0.05
0.047
fulfilled
The analysis in Table 4, shows that indicators
Goodness of Fit were fulfilled. This means that the
conceptual model of the proposed MCTS test is fit
with the data.
3.4 Mathematical Creative Thinking
Skill (MCTS)
Students' overall mathematical creative thinking
skills (MCTS) are presented in Table 5.
Table 5: Descriptive statistics of students' MCTS
N
Valid
180
Missing
0
Mean
50.27
Median
48.00
Mode
48
Std. Deviation
10.272
Variance
105.524
Skewness
.525
Std. Error of Skewness
.181
Kurtosis
.206
Std. Error of Kurtosis
.360
Range
48
Minimum
30
Maximum
78
It can be seen from Table 5, as a whole from 180
students as respondents, indicating that students'
mathematical creative thinking skills are still low in
level.
Visually the distribution of students' MCTS data,
as a whole is presented in Figure 3. Based on Figure
3, it is found that the MCTS data distribution has a
tendency to collect below the empirical average.
This means that the MCTS data distribution is
grouped below the average. Thus the ability of
MCTS students is still relatively low.
Figure 3: Frequency Histogram of students’ MCTS as a
whole
Students’ MCTS data by gender score in Table 6.
Table 6: Data on sudents’ MCTS
Statistics
Mathematical Creative
Thinking Skills (MCTS)
Male
Female
Total
N
98
82
180
Std. Deviation
1274
13.32
10.27
Mean
49.54
61.45
50.27
Median
48.75
49.88
48.00
Modus
50.83
52.50
48.00
Minimum
33
45
30
Maximum
70
83
78
The results of the analysis in Table 6, show that
from 180 students as respondents, an average score
of 50.27, a maximum value of 78 and a minimum of
30, a median of 48.00, Mode 48, and Std. Deviation
10.27. This finding reveals that the ability of
students' MCTS is still relatively low.
The findings of this study, similar to the research
of (Fitriani & Yarmayani, 2018) who developed the
MCTS rubric of students of Senior High School,
found that the classification of highly creative
abilities (75-96) was 0%, creative (50-74) as much
as 39.13 %, quite creative (25-49) of 60.86%, and
less creative (0-24) as much as 0% [12]. From Table
IV, also obtained the average MCTS score of male
students was 49.54 and female was 61.45. This
means that MCTS female students are higher than
male students. The findings of this study are in
accordance with the opinion of Krutestkii (Nafi’an,
2011), explaining that men are superior in reasoning,
women are superior in precision, accuracy, and more
careful in thinking. Men have better mathematical
and mechanical abilities than women, this difference
Measuring Construct Validity and Students’ Mathematical Creative Thinking Skills
671

is not apparent at the basic level but becomes more
apparent at a higher level.
Furthermore, student scores on each indicator
from MCTS based on the school in the Table 7.
Table 7: average student scores for each MCTS indicator
and school
Schoo
l
N
Average students' MCTS for each
indicator
Mean
Fluency
Elabor
Flexi
Origin
A
30
71.17
42.70
64.33
29.93
52.03
B
30
61.90
29.30
69.83
24.70
46.43
C
30
70.17
30.60
69.03
33.27
50.77
D
30
75.90
48.63
83.60
52.50
65.16
E
30
63.00
26.93
63.57
26.63
45.03
F
30
59.53
27.63
58.13
23.50
42.20
Mean
18
0
66.95
34.30
68.08
31,76
50.27
Based on the results of the analysis in Table 7,
the students' ability score on the fluency indicator is
66.95, elaboration is 34.30, flexibility is 68.08 and
originality is 31.76. Research findings confirm that
flexibility is an indicator that is better than fluency,
elaboration, and originality. The fluency indicator is
the ability to provide many answers, then the
elaboration indicator, namely the ability to write
information that is known to the problem. While the
flexibility indicator is the ability to provide
alternative ways to solve problems, and the
originality indicator is to produce unusual or unique
answers according to quadrilateral geometry. The
findings of this study are somewhat different from
the findings of (Fatimatuzahro & M Budiarto, 2014),
who reported that students with high mathematical
abilities had better creative thinking skills on
indicators of fluency and elaboration, while students
with moderate math ability were only better at
fluency indicators and students with low abilities did
not show creative thinking skills.
3.5 Test the Influence Hypothesis
among the MCTS Indicators
Hypothesis test results of the influence between the
MCTS indicators in Table 8.
Table 7: Results of influence among the MCTS indicators
Influence among
indicator
Est
S.E.
C.R.
p
Elaboration 
Fluency
.235
.054
3.234
.001
Flexibility  Fluency
.053
.070
.700
.484
Flexibility 
Elaboration
.166
.093
2.201
.028
Influence among
indicator
Est
S.E.
C.R.
p
Originality 
Flexibility
.200
.074
2.708
.007
Originality 
Elaboration
.052
.094
.689
.491
Originality  Fluency
.080
.069
1.068
.285
Based on the analysis results in Table 8, it shows
that the indicators: (1) fluency has an influence on
the elaboration indicator (p = 0.001 <0.05); (2)
fluency has an influence on flexibility (p = 0.484>
0.05); (3) elaboration has an influence on flexibility
(p = 0.028 <0.05); (4) flexibility has an influence on
originality (p = 0.007 <0.05); (5) elaboration has no
effect on originality (p = 0.491> 0.05); (6) fluency
does not have an influence on the originality
indicator (p = 0.285> 0.05). Thus the hierarchy of
influence according to the MCTS indicator starts
from the lowest position of fluency, elaboration,
flexibility and the highest position on originality.
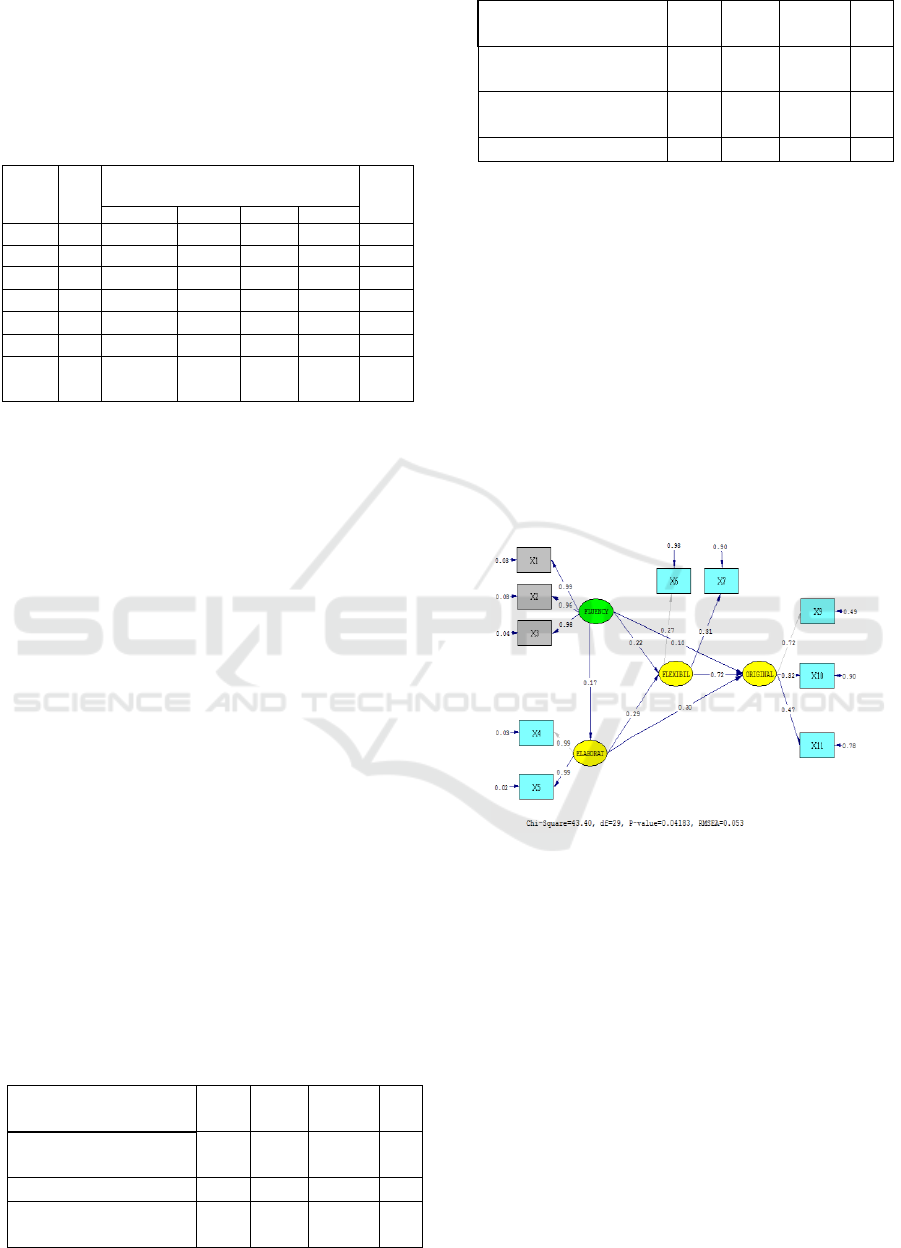
Visually the relationship between MCTS items
and indicators in Figure 4.
Figure 4: Relationship between test items and indicators
The research findings revealed that the students'
MCTS on the fluency indicator had a positive effect
on students' ability on the elaboration indicator.
Thus the higher the ability of students in the fluency
indicator, the higher the ability of students in
elaboration skills. This finding shows that the ability
to provide many ideas in determining the area and
circumference of the rectangle supports the students'
ability to enrich the detailed information of
rectangular Geometry problems. While the ability of
students on the elaboration indicator has a positive
effect on students' ability in flexibility. This means
that the ability of students on the elaboration
indicator determines students' abilities on flexibility
indicators. Thus the higher the student's ability in the
elaboration indicator, the higher the student's ability
ICRI 2018 - International Conference Recent Innovation
672

in flexibility. This finding confirms that students'
ability to detail details of information or data from a
rectangular flat geometry problem helps students
make several different interpretations in solving
rectangular-related problems.
Furthermore, the ability of students on the
flexibility indicator has a positive effect on students'
abilities in the originality indicator. This means that
the ability of students on the flexibility indicator can
actually explain students' abilities in the originality
indicator. This finding describes that the ability to
produce ideas, answers or questions that vary, can
see problems from different points of view, and are
able to find many alternatives or different directions
from the problem of rectangular geometry to a
capacity to express new and unique things, thinking
of unusual ways, and making unusual combinations
of rectangular elements.
The findings of this study also provide a
distinctive and novelty related to the MCTS test
measuring indicator, namely that through path
analysis between indicators, we find a hierarchy of
abilities as a sequence of abilities that starts from the
fluency indicator then elaboration, flexibility and
ends in the originality indicator as the highest ability
in creative thinking.
The following are examples of questions and
student answers to the originality indicator.
"Pay attention to the right triangle below. The
BR line is parallel to the PQ line with point P as the
midpoint of the BC line. Determine the area to be
shaded? "
A
B
P
6 cm
6 cm
Q
R
8 cm
C
Students' answers to the questions above are made in
two ways, namely:
Answer 1:
By constructing the flat trapezium into a rectangle
and parallelogram.
From this picture the area of shading = 1/2 the area
of parallelogram, while area of parallelogram = area
of rectangular area - 2 area of triangle.
Area of parallelogram = (6 x 8) –2 (½(4 x 6)) =
48 – 24 = 24 cm
2
. Dhus area of shading = 1/2 area
of parallelogram = ½ x 24 = 12 cm
2
Answer 2:
Draw a line from one of the trapezium points to
another.
A
It is seen that the area of the trapezium is formed of
several triangles. Dhus area of shading = 1/2 the area
of ABC right triangle = ½ x ½ (6 x 8) = ¼ x 48 = 12
cm
2
.
Thus the core of MCTS is developing the ability
to focus on the originality indicators. As with
Sriraman's definition, that mathematical creativity is
the ability to produce original works that
significantly extends the body of knowledge
(Sriraman, 2005). To maximize MCTS in the
originality indicator, the flexibility capability is
needed. While increasing flexibility is determined by
fluency and elaboration abilities. This finding
confirms that the role of fluency indicator capability
on originality can be mediated by indicators of
elaboration and flexibility. We believe that these
findings are new findings that complement previous
studies related to the ability to think creatively in
mathematics learning.
4 CONCLUSION
Based on the findings and discussion, it can be
concluded that the MCTS test is valid and
consistently measured through constructs or
indicators of fluency, elaboration, flexibility, and
originality. Overall, the MCTS test construct has an
internal consistency of 0.815 or a very good
Measuring Construct Validity and Students’ Mathematical Creative Thinking Skills
673

category. MCTS test consists of 10 items and four
indicators, namely fluency consisting of 3 items with
loading factors (0, 986; 0.961; 0.978) and construct
reliability of 0.952; elaboration consists of 2 items
with loading factors (0.986; 0.990) and construct
reliability of 0.976, Flexibility consists of 2 items
with loading factors (0.277; 0.359) and construct
reliability of 0.622, and originality consists of 3
items with loading factors (0.713; 0.319; 0.473) and
construct reliability of 0.710.
The overall MCTS of students is still relatively
low, which is an average of 50.27 on a scale (0-100).
Achievement the highest MCTS of students is
obtained in the flexibility indicator of 68.08; then the
fluency is 66.95, elaboration is 34.30, and the lowest
is the originality indicator 31.76. The average MCTS
of female students is 61.45 and male students are
49.54. Thus, MCTS of female students are quite
good and higher than male students. The influence
of ability on the fluency indicator on originality is
mediated by indicators of elaboration and flexibility.
The ability to solve problems in the originality
indicator is the core of students' creative thinking
ability. Therefore, it is suggested that to improve
students' creative thinking skills students should
begin gradually from problems that measure fluency
indicator abilities then elaboration, flexibility and
end with originality. To maximize students' ability to
think creatively mathematically on the originality
indicator, the best performance is needed on the
flexibility indicator. While increasing flexibility is
determined by fluency and elaboration abilities.
REFERENCES
Bosch, N. (2008). Rubric for Creative Thinking Skills
Evaluation. Kansas: KCCL.
Fardah, K. D. (2012). Analisis Proses dan Kemampuan
Berpikir Kreatif Siswa dalam Matematika Melalui
Tugas Open-Ended. Jurnal KREANO FMIPA UNNES,
3.
Fatimatuzahro, & M Budiarto. (2014). Identifikasi
Kemampuan Berpikir Kreatif Siswa SMP dalam
Menyelesaikan Soal Matematika Open-Ended Ditinjau
dari Perbedaan Kemampuan Matematika. Jurnal
MATHEdunesa Jurusan Matematika UNESA, 3, 85–
89.
Fitriani, S., & Yarmayani, A. (2018). Pengembangan
Rubrik Berpikir Kreatif Siswa Menengah Atas Dalam
Menyelesaikan Masalah Matematika. Jurnal
Mosharafa, 7.
Fitriarosah, N. (2016). Pengembangan Instrumen Berpikir
Kreatif Matematis Untuk Siswa SMP. Prosiding
Seminar Nasional Pendidikan Matematika, Malang:
Universitas Kanjuruhan Malang.
Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E.
(2010). Multivariate data analysis (7th ed.). New
Jersey: Pearson Prentice Hall.
Hendriana, H., & Sumarmo, U. (2014). Penilaian
Pembelajaran Matematika. Bandung: PT Refika
Aditama.
Kadir, Lucyana, & Satriawati, G. (2017). The
Implementation Of Open-Inquiry Approach To
Improve Students’ Learning Activities, Responses,
and Mathematical Creative Thinking Skills. Journal
on Mathematics Education, 8, 103–114.
Moma, L. (2015). Pengembangan Instrumen Kemampuan
Berpikir Kreatif Matematis untuk Siswa SMP. Delta-
Pi:Jurnal Matematika Dan Pendidikan Matematika, 4.
Nafi’an, M. I. (2011). Kemampuan Siswa Dalam
Menyelesaikan Soal Cerita Ditinjau Dari Gender Di
Sekolah Dasar. Prosiding Seminar Nasional
Matematika Dan Pendidikan Matematika, Jurusan
Pendidikan Matematika FMIPA UNY, 573 – 574.
Novita, R., Zulkardi, Z., & Hartono, Y. (2012). Exploring
Primary Student’s Problem Solving Ability by Doing
Tasks Like PISA’s Question. IndoMS, J.M.E, 3(2),
133–150. https://doi.org/10.1007/s13398-014-0173-
7.2
PISA. (2015). No Titl. Results Excellence and Equity in
Education, 1.
Saini, R. A. (2015). Inovasi pembelajaran. Jakarta: Bumi
Aksara.
Siswono, T. Y. E. (2008). Model Pembelajaran
Matematika Berbasis Pengajuan Masalah dan
Pemecahan Masalah untuk Meningkatkan
Kemampuan Berpikir Kreatif. Surabaya: Unesa
University Press.
Sriraman, B. (2005). Are giftedness & creativity
synonyms in mathematics? An analysis of constructs
within the professional and school realms. The Journal
of Secondary Gifted Education, 17, 20–36.
Sternbergn, R. J. (2001). Wildson, Intelligence, and
Creativity Synthesized. New York: Cambridge
University Press.
Sternbergn, R. J., & Lubart, T. L. (2000). The Concept of
Creativity: Prospects and Paradigms. In R.J.
Sternbergn (Ed.), Handbook of Creativity (pp. 27–39).
New York: Cambridge University Press.
ICRI 2018 - International Conference Recent Innovation
674