
A Modified iMOEA/D for Many-objective Optimization Problems
with Complicated Pareto Fronts
Ghizlane Aboulbaroud
1
and Driss Mentagui
2
1
Applied Mathematics Laboratory, Faculty of Sciences, Ibn Tofail University, Kenitra, Moroccoo
2
Dr Professor, Applied Mathematics Laboratory, Faculty of Sciences, Ibn Tofail University, Kenitra, Moroccoo
Keywords: Evolutionary algorithm, many-objective optimization, decomposition, Pareto front, MOEA/D, IPBI
approach.
Abstract: In real life, multiobjective evolutionary algorithms have many areas of applications, such as intelligence
transportations systems, management problems, data mining, data-analysis and so on. Due to the importance
of these problems, researchers have investigated several approaches to deal with them. Decomposition is
one of the basic strategies used in multiobjective evolutionary optimization. In this paper, a modified
iMOEA/D evolutionary algorithm based decomposition is suggested. This proposition allows dealing with
Many-objective optimization problems with complicated Pareto fronts. The performance of this algorithm is
demonstrated using a set of benchmark problems in comparison with other recently proposed algorithms.
1 INTRODUCTION
In the majority of real life problems, many
objectives (often conflicting) need to be optimized
simultaneously. In that case, the output is not a
single optimal solution but rather a set of possible
solutions called the optimal Pareto set.
Aggregating the multiple objectives into one
objective function is the simplest method to deal
with an optimization problem of a multiobjective
nature. The most widely used method is the
weighted sum method. However, the drawback of
this approach is that it is not always possible to find
the appropriate weighted function.
Multiobjective Optimization deals with such
simultaneous optimization of multiple, possibly
conflicting, objective functions, without combining
them in a weighted sum. The set of solutions of a
Multiobjective Optimization Problem (MOP) is
composed of the parameter vectors, which cannot be
improved in any objective without degrading in at
least one of the objectives, and this set called the
Pareto optimal set and its image in the objective
function space is usually called the Pareto front (PF).
Multiobjective Evolutionary Algorithms have
been recognized as the promising techniques for
solving multiobjective optimization problems. As
well as the domination based and the performance
indicator based algorithms, the multiobjective
evolutionary algorithms based on decomposition
(MOEA/D) (Zhang et al., 2014) have been widely
used and investigated recently and they have shown
its effectiveness. In MOEA/D, a MOP is
decomposed into single objective optimization sub-
problems and then solved in a single run. The
objective function in each sub-problem can be a
linear or nonlinear weighted aggregation function of
all the objective functions in the concerned MOP.
The main used approaches for converting MOP into
scalar sub-problems are: Weighted Sum (WS)
Approach, Tchebycheff (TCH) Approach and
Boundary Intersection (PBI) Approach.
These approaches have been widely detailed in
literature (Trividi et al., 2016). MOEA based
decomposition have shown its effectiveness in the
real-world applications.
Many-objective optimization (MaOPs) problems
(four or more number of objectives) are currently a
subject of great interest for the scientific research
94
Aboulbaroud, G. and Mentagui, D.
A Modified iMOEA/D for Many-objective Optimization Problems with Complicated Pareto Fronts.
DOI: 10.5220/0009774000940101
In Proceedings of the 1st International Conference of Computer Science and Renewable Energies (ICCSRE 2018), pages 94-101
ISBN: 978-989-758-431-2
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

community. A great number of algorithms have been
developed to solve this class of problems. In (Trividi
et al., 2016), a summary of studies on MOEAs based
on decomposition for many-objective optimization is
given.
In this article, we propose an improved MOEA/D
which deals with many-objective optimization
problems with complicated Pareto fronts. The
developed algorithm is based on recent research
papers (Hohuu et al., 2018) and (Zhang et al., 2014).
Our main contributions include the following
aspects:
Idea 1: We adopt the PBI approach in the first
phase for its effectiveness in handling Maops.
Idea 2: we adopt the inverted PBI scalarizing
approach to deal with problems with complicated
Pareto fronts.
This paper is organized as follows: section 2
summarizes the basic concepts and defintitions
related to evolutionary algorithms based
decomposition framework and introduces related
works. Section 3 presents our detailed algorithm.
Analysis and discussion are shown in section 4
followed by conclusion.
2 PRELIMNINARIES AND
RELATED WORKS
In this section, basic definitions and concepts are
presented and related works are introduced
2.1 Basic Definitions
Definition 1: Many-objective Optimization
Problem
A Many-objective Optimization Problem MaoP (1)
can be formulated as:
min
,…,
1
∈Ω
Where
,…,
is the decision variables
vector, Ω is the search space and is the number of
objective functions.
Definition 2: Domination
We say that a solution dominates a solution if
and only if is better than or equal to in all
objectives and better than in at least one.
predefined by the user.
is used to measure
convergence and
is used to measure diversity. A
solution with small
and
is considered as a
better solution close to the Pareto front.
Another decomposition approach is introduced. This
method is used in our proposed algorithm.
- The IPBI-Approach
Traditional decomposition approaches face difficulty
in approximating widely spread PF in some
problems like MOKPs (Sato, 2015). To deal with
this problem and to conceive a decomposition
method performant for many-objective optimization,
inverted PBI (IPBI) decomposition method is
proposed (Sato, 2015). In the conventional
decomposition methods such as the TCH and the
PBI, solutions are evolved towards the reference
point z by minimizing the scalarizing function value.
However, in the IPBI approach, solutions are
evolved from the nadir point by maximizing the
scalarizing function value. The experiments on
MOKPs and WFG4 problem (Sato, 2015), with 2-8
objectives, demonstrated that the IPBI approach can
better approximate widely spread PF in comparison
to other scalarizing approaches.
The expression of the Inverted Penalty Boundary
Intersection is given by:
|
6
Where
‖
‖
7
‖
‖
MOEA/D has been extended to several variants
using different decomposition approaches. The
MOEA/D has shown its effectiveness to outperform
NSGAII (Deb et al., 2002) and other existing
A Modified iMOEA/D for Many-objective Optimization Problems with Complicated Pareto Fronts
95

algorithms based decomposition (Zhang et al.,
2007).
In (Jiang et al., 2016), Jiang et Yang have
proposed MOEA/D-TPN to solve problems with
complex Pareto fronts. A two-phase strategy is
adopted. The TP strategy, which conditionally
divides the whole optimization process into two
phases and the niche-guided strategy, which helps
maintain the population diversity. The detail of this
algorithm is given in (Jiang et al., 2016).
In MOEA/D-AWA (Qi et al., 2014), Qi et al.
proceed in two stages strategy. In the first stage, a
set of weight vectors are used until the algorithm
converge to a certain extent. Then, to handle MOPs
with complex Pareto fronts an adaptive weight
vectors adjustment strategy is adopted.
The NSGA III algorithm proposed in (Deb et al.,
2014) is an improved version of NSGA II
framework. This algorithm can deal with many-
objective optimization problems using reference
points to implicitly decompose the objective space
and a niche preservation operator to increase
diversity of solutions close to every reference point.
The studies prove that NSGA III performs well than
MOEA/D-PBI and MOEA/D-TCH (Deb et al.,
2014). More detail is presented in (Deb et al., 2014).
RVEA (Cheng et al., 2016) is another algorithm
for solving many-objective optimization problems.
Cheng et al. adopt a reference vectors reconstruction
strategy and use a new scalarizing approach, namely
angle-penalized distance (APD). RVEA can deal
with MOPS with irregular Pareto Fronts and can
guarantee a uniform distribution of the reference
vectors. However, RVEA is unable to handle Pareto
fronts with long tails or sharp peaks (Cheng et al.,
2016).
iMOEA/D Concept
Combining the ideal point
∗
and nadir point
in Tchebycheff functions was reported as an
effective way to get a good distribution of optimal
solutions over a Pareto front. This combination
allows dealing with multiobjective optimization
problems characterized by complex fronts (Zhou et
al., 2017). Based on this, in (Jiang et al., 2016),
Jiang have designed an evolutionary algorithm
proceeding in two phases. Where the Tchebycheff
function with
∗
is employed in the first phase and
the Tchebycheff function with
is used in the
second phase. The second phase will only be
executed if a condition on the first phase is satisfied.
This strategy presents limitations that have been
overcome by Ho-huu in (Hohuu et al., 2018). These
limitations concern the difficulty of setting a number
of evaluations to pass from phase 1 to phase 2 and
the computational cost of solving a multiobjective
optimization problems if phase 2 is executed. In
(Hohuu et al., 2018), Ho-huu proposed an improved
MOEA/D (iMOEA/D) to deal with MOP with
complex fronts and to overcome the limitations
already mentioned. A new two phase strategy is
proposed. This strategy consists of dividing the
weights vector into two subsets: odd weight vectors
and even weight-vectors. In the first phase, the
population of the first subset is optimized using the
Tchebycheff function with the ideal point
∗
. The
Tchebycheff function with the nadir point is applied
for the second subset. The
is obtained from
the set solutions found in the first phase. The
algorithm proposed in (Hohuu et al., 2018) has
shown its effectiveness and competitiveness than
MOEA/D, MOEAD/TPN (Jiang et al., 2016) and
NSGA II, through many test functions with
complicated Pareto fronts. However, it is limited to
bi-objective optimization problems and cannot deal
with problems with more than 2 objective functions.
The pseudo-code of iMOEA/D (Ho-huu, 2018) is
given in Algorithm 1.
The iMOEA/D version includes some recent
developments related to MOEA/D which are an
adaptive replacement strategy (Zhang et al., 2009)
and a stopping criterion introduced in (Baskar et al.,
2016).
In the following section, we describe our
proposed algorithm.
Algorithm 1: iMOEA/D
Input: A MOP, subsets of odd and even weight
vectors, N subproblems,
Phase (1)
Initialization
Decomposition using the Tchebycheff function with
ideal point and the subset of the odd-weight vectors.
Update
Stopping criteria and output PS1 and PF1
Phase (2)
Initialization
Decomposition using the Tchebycheff function with
the z nadir and the subset of the even-weight vectors.
Update
Stopping criteria and output PS2 and PF2
PS=
1,2 Pareto set
PF=
1,2 Pareto front
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
96

3 PROPOSED ALGORITHM
This paper is a modified version of the iMOEA/D
algorithm proposed by (Ho-huu et al, 2018). The
said algorithm handles bio-objective optimization
problems with complicated Pareto fronts. To extend
the scope of this algorithm and make it suitable for
Many-objective optimization problems, we propose
a modified iMOEA/D which deals with many-
objective optimization problems (MaOP)
characterized by a complex Pareto front.
In our algorithm, we use both the PBI and the
inverted PBI scalarizing approaches.
We proceed in two phases. In the first phase we
run our algorithm using the PBI approach with the
set of the odd-weight vectors and the ideal point
∗
.
In the second phase, the Inverted PBI approach is
applied with the set of the even-weight vectors
and
. The
is determined using the
solutions obtained from the first phase.
Reasons behind using the PBI and the inverted
PBI approaches:
The Penalty Boundary Intersection is widely
applied in MOEA/D. In most cases, a uniform
distribution of weight vectors in PBI approach will
outcome a set of evenly distributed solutions on the
Pareto-optimal front (POF). The PBI-approach has
shown its performance for solving many-objective
optimization problems and to handle problems with
complex Pareto fronts, we apply the inverted PBI
approach in the second phase.
4 EXPERIMENTS AND RESULTS
In this section, we test our algorithm along with a set
of well-known algorithms including NSGA III,
RVEA and MOEA/D-PBI.
4.1 Test Problems
We use DTLZ1, DTLZ2, DTLZ3 and DTLZ4 to test
the ability of our algorithm to deal with more than 2
objectives. Table 1 describes the test instances, their
variable domains and instance characteristics used in
this work.
4.2 Parameters Setting
The population size in each algorithm is set to 800
for all test instances. The maximum number of
Algorithm 2 Main algorithm
Input:
A multiobjective optimization problem MOP,
N number of sub-problems
A StoppingCriterion
,…,
,,,…,: a set of odd-
weight vectors;
,…,
,,,…,: a set of
even-weight vectors;
: size of mating neighborhood;
: maximum size of replacement neighborhood;
: the probability for selection the mating parents
from the neighborhood;
: maximum iteration;
Output: Approximation to the PF
Phase (1)
Initialization
Set
the initial population,
∗
the ideal point
and
and
Set
: size of mating neighborhood
and maximum size of replacement neighborhood
Set
,…,
as mentioned in (Zhang et al.,
2014)
.
Decomposition using PBI scalarizing function
and
with
∗
.
Solution building: a solution is generated using the
‘DE/rand 1’ operator
Update solution
Stopping criterion and output PS1 and PF1
Phase (2)
Initialization
Define
with
∈,,…,
∈
Set the initial population
Decomposition using inverted PBI scalarizing
function and
with
Solution building
Update
Termination criterion and output PS2 and PF2
Output
PS={PS1,PS2}
PF={PF1,PF2}
A Modified iMOEA/D for Many-objective Optimization Problems with Complicated Pareto Fronts
97

generations was set to 400 for all test instances. For
the MOEA/D-PBI and our proposed algorithm, is
set to 5.
4.3 Results and Discussion
The inverted Generalized Distance (IGD) Indicator
is used to indicate both the convergence and the
diversity of our algorithm. The table 2 shows that
our proposed algorithm M-iMOEA/D could perform
well on all of the test instances especially on DTLZ1
and DTLZ4.
5 CONCLUSIONS
In this paper, we develop a modified version of
iMOEA/D (Hohuu et al., 2018) named (M-
iMOEA/D) for solving MaOPS with complicated
Pareto fronts. In M-iMOEA/D, we adopt a two
phase strategy. In the first strategy, the set of the
odd-weight vectors is selected to be optimized using
the PBI approach with the ideal point
∗
. In the
second phase, the Inverted-PBI approach is applied
with the set of even-weight vectors and
which
is determined from the set of the obtained solutions
of the first stage. Our algorithm shows its
performance than other algorithms in problems with
many-objectives and complicated Pareto fronts by
using a set of benchmark problems.
REFERENCES
V. Ho-Huu, S. Hartjes, H. G. Visser, and R. Curran, « An
improved MOEA/D algorithm for bi-objective
optimization problems with complex Pareto fronts and
its application to structural optimization », Expert
Systems with Applications, vol. 92, p. 430
‑
446, feb.
2018.
Y. Zhou, Y. Xiang, Z. Chen, J. He, and J. Wang, « A Scalar
Projection and Angle-Based Evolutionary Algorithm
for Many-Objective Optimization Problems », IEEE
Transactions on Cybernetics, p. 1-12, 2018.
S. Jiang and S. Yang, « An Improved Multiobjective
Optimization Evolutionary Algorithm Based on
Decomposition for Complex Pareto Fronts », IEEE
Transactions on Cybernetics, vol. 46, no 2, p.
421-437, Feb. 2016.
A. Trivedi, D. Srinivasan, K. Sanyal, and A. Ghosh, « A
Survey of Multiobjective Evolutionary Algorithms
based on Decomposition », IEEE Transactions
on Evolutionary Computation, p. 1-1, 2016.
Xinye Cai, Yexing Li, Zhun Fan, and Qingfu Zhang, « An
External Archive Guided Multiobjective Evolutionary
Algorithm Based on Decomposition for Combinatorial
Optimization », IEEE Transactions on Evolutionary
Computation, vol. 19, no 4, p. 508
‑
523, Aug 2015.
M. Nasir, A. K. Mondal, S. Sengupta, S. Das, and A.
Abraham, « An improved Multiobjective Evolutionary
Algorithm based on decomposition with fuzzy
dominance », 2011, p. 765
‑
772.
C. A. C. Coello, « An updated survey of evolutionary
multiobjective optimization techniques: state of the art
and future trends », 1999, p.3
‑
13.
H.-L. Liu, F. Gu, and Q. Zhang, « Decomposition of a
Multiobjective Optimization Problem Into a Number
of Simple Multiobjective Subproblems », IEEE
Transactions on Evolutionary Computation, vol. 18,
no 3, p. 450
‑
455, June 2014.
Qingfu Zhang and Hui Li, « MOEA/D: A Multiobjective
Evolutionary Algorithm Based on Decomposition »,
IEEE Transactions on Evolutionary Computation, vol.
11, no 6, p. 712
‑
731, dec. 2007.
H. Sato, « Analysis of inverted PBI and comparison with
other scalarizing functions in decomposition based
MOEAs », Journal of Heuristics, vol. 21, no 6, p.
819-849, dec. 2015.
M. Asafuddoula, T. Ray, and R. Sarker, « A
Decomposition-Based Evolutionary Algorithm for
Many Objective Optimization », IEEE Transactions on
Evolutionary Computation, vol. 19, no 3, p. 445-460,
June 2015.
H. Li, Q. Zhang, « Multiobjective Optimization Problems
with Complicated Pareto Sets, MOEA/D and NSGA-
II », IEEE Transactions on Evolutionary Computation,
vol. 13, no 2, p. 284-302, apr. 2009.
K. M. Abdul Kadhar and S. Baskar, « A stopping
criterion for decomposition-based multi-objective
evolutionary algorithms », Soft Computing, vol. 22, no
1, p. 253-272, janv. 2016.
K. Deb, A. Pratap, S. Agarwal and T. Meyaruvan , «A
fast and elitist multiobjective genetic algorithm:
NSGA-II» Evolutionary Computation, IEEE
transactions on Evolutionary Computation, vol. 6, no.
2, p. 182-197, Apr 2002.
E. Zitzler, M. Laumanns and L. Thiele, « SPEA II,
Improving the strength Pareto Evolutionary algorithm
for multiobjective optimization » in Evolutionary
Methods dor Design, Optimization, Control. CIMNE,
p. 95-100, Spain 2002.
Y. Qi, X. Ma, F. Liu, L. Jiao, « MOEA/D with adaptive
weight adjusment, Evolutionary Computation. P. 231-
264, 2014.
K. deb and H. Jain « An evolutionary many-objective
optimization algorithm using reference point based
non-dominated sorting approach, Part I: Solving
problems with box constraints », IEEE Transactions
on Evolutionary Computation, Vol. 18, no. 4, p. 577-
601, 2014.
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
98

R. Cheng, Y. Jin, M. Olhofer and B. Sendhoff, « A
reference vector guided evolutionary algorithm for
many objective optimization », IEEE Transactions on
Evolutionary Computation, no. 99, p1-1, 2016.
Z. Wang, Q. Zhang, M. Gong andA. Zhou, « A
replacement strategy for balancing convergence and
diversity in MOEA/D», Evolutionary Computation,
IEEE Trans, p. 2132-2139, Jul, 2014.
K. Deb, L. Thiele, M. Laumanns, E. Zitzler, « Scalable
test problems for multiobjective optimization,
Springer, 2005.
Table 1: Benchmark problems: DTLZ1, DTLZ2, DTLZ3, DTLZ4
Problem Objective function Domain Characteristics
DTLZ1
0.5
…
1
0.5
…1
1
.
.
0.5
1
1
0.51
1
100
|
|
0.5
cos20
0.5
∈
0,1
Linear,
multimodal
DTLZ2
cos
2
…cos
2
cos
2
1
cos
2
…cos
2
sin
2
1
.
.
.
cos
2
sin
2
1
sin
2
1
0.5
∈
0,1
Concave
DTLZ3
cos
2
cos
2
…cos
2
cos
2
1
cos
2
cos
2
…cos
2
sin
2
1
.
.
.
cos
2
sin
2
1
sin
2
1
100
|
|
0.5
∈
cos20
0.5
0,1
Concave,
multimodal
A Modified iMOEA/D for Many-objective Optimization Problems with Complicated Pareto Fronts
99
DTLZ4
cos
2
cos
2
…cos
2
cos
2
1
cos
2
cos
2
…cos
2
sin
2
1
.
.
.
cos
2
sin
2
1
sin
2
1
0.5
∈
.100
0,1
Concave,
biased
Table 2: the obtained IGD average values obtained for DTLZ1-DTLZ4 test problems
M M-iMOEA/D NSGA-III RVEA MOEA/D-PBI
DTLZ1
3
3.0001e-02
3.0938e-01 5.0488e-01 3.4647e-02
4 5.4290e-02
7.7805e-02 1.2131e-01 5.4289e-02
5
6.5003e-02
5.6473e-01 3.4217e-01 6.5954e-02
DTLZ2
3 5.4769e-02
5.4920e-02 5.8780e-02 5.4643e-02
4
1.4009e-01
1.4090e-01
1.4072e-01 1.1412e-01
5
2.1905e-02
2.1626e-02
2.1396e-01
2.1318e-01
DTLZ3
3
1.7896e-01
1.0704e+01 8.8125e-00 1.8099e-01
4
1.7969e-01
1.6565+01 1.8081e-01 1.8020e-01
5 1.1060e-01
9.8374e-00 1.0358e-01 1.1361e-01
DTLZ4
3 5.3936e-02 5.7025e-02
5.255e-02 5.4151e-01
4
1.4078e-01
1.4227e-01
1.4089e-01 7.5111e-01
5
2.1101e-01
2.1833e-01 2.1487e-01 6.4572e-01
ICCSRE 2018 - International Conference of Computer Science and Renewable Energies
100

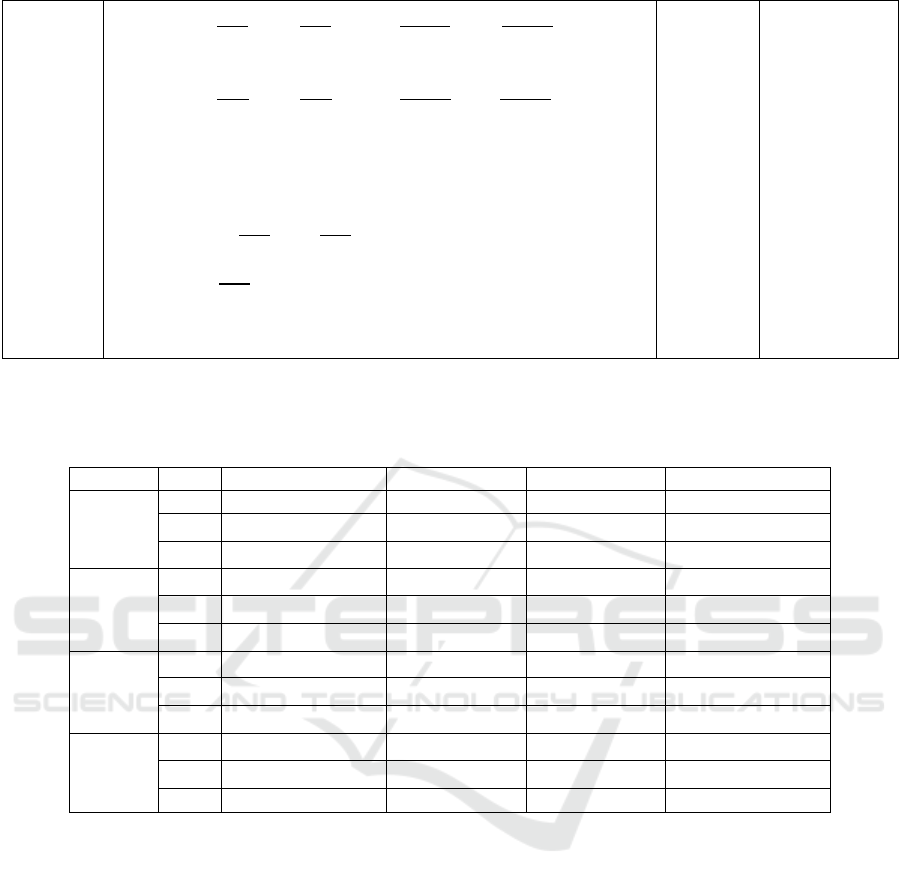
Figure 1: Parallel cordinates of PFs obtained by four algorithms :(1) RVEA, (2) NSGAIII, (3), MOEAD-PBI, (4) M-
iMOEAD
DTLZ1 (1) (2) (3) (4)
DTLZ2
DTLZ3
DTLZ4
A Modified iMOEA/D for Many-objective Optimization Problems with Complicated Pareto Fronts
101
