
Identifying Mathematics Education Students’ Obstacles
in Reading and Constructing Proofs in Real Analysis Courses
Hasan Hamid
Mathematics Education Study Program, Universitas Khairun, Ternate, Indonesia
Keywords: Learning obstacles, the ability to read proof, to construct proof.
Abstract: This study aims to find out how students’ experiences and obstacle in learning the Real Analysis lectures
that they have experienced. The aspects measured are: (1) the ability to read and understand a proof, and (2)
The ability to construct a proof. Subjects in this study consisted of 43 students of Mathematics Education
Study Program of FKIP Khairun University and data were collected through tests and interviews. Interviews
were conducted with six students based on the work to identify the obstacles experienced in reading,
understanding and constructing a proof. The data were analyzed by using the descriptive-qualitative
approach. The results show that the ability to read, understand and construct a proof belong to the medium
category.
1 INTRODUCTION
In general, obstacles are anything that hinders
student learning (Moru, 2007), based on some
writings on obstacles according to Tall (1991),
which have identified three forms of obstacles,
usually related to students' failure to accommodate
new ideas. These obstacles are epistemological,
cognitive, and didactic. Epistemological nature,
more because of the internal reasons of mathematics
itself (Brousseau, 1997; Sierpinska, 1987); cognitive
traits, because of the abstraction process and
conceptualization involved in it (Cornu, 1991;
Dubinsky, 1991; Sfard, 1991; Tall & Vinner, 1981)
while didactic traits, due to the nature of teaching
and learning (Brousseau, 1997).
Proof activities are important in mathematics
education, especially in Real Analysis, where most
of the material is in the form of proof tasks related to
lemma, theorems, and corollary. The activity of
constructing a proof in real analysis is one of the
obstacles that are often encountered by students,
even though in constructing the proof some
instructions have been given to facilitate the
construction of proof.
According to Selden and Selden (2003) one of
the important activities in mathematics is to read
mathematical proof with the aim of determining
whether the proof is valid or not, this activity is
marked as proof validation and this is a complex
process involving evaluation of arguments,
proposing and answer questions, construct sub
proof, remember definitions and theorems.
Furthermore Selden and Selden (Pfeiffer, 2010)
assert that the ability to read proof is the ability to
determine truth from mathematical proof and mental
processes related to validation of proof. Validation
not only determines the truth of the argument, but
the validation of the proof includes: does the reader
understand the argument provided?, the quality and
clarity of the idea of the proof strategy, the clarity of
the structure, the selection of appropriate, correct
and adequate reasons, and what is the convincing
argument? While the mental process when
validating proof is asking or answering questions,
constructing parts of proof or remembering theorems
and other definitions.
Referring to "transactional theory of reading",
Rosenblant (1988) suggests that during reading
activities, the reader forms and is actively formed by
the text. So the reader does not only recite the
readings, but with the knowledge, interest and
curiosity of the text being read, the reader will try to
develop the meaning of the text. If this is associated
with the ability to read proof from a student, then the
student can express ideas/ideas contained in the
proof both verbally and in writing using his own
language and understand what is contained in the
mathematical proof.
264
Hamid, H.
Identifying Mathematics Education Studentsâ
˘
A
´
Z Obstacles in Reading and Constructing Proof in Real Analysis Courses.
DOI: 10.5220/0008900602640268
In Proceedings of the 1st Inter national Conference on Teaching and Learning (ICTL 2018), pages 264-268
ISBN: 978-989-758-439-8
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
Constructing proof requires the right idea at the
right time, so that it requires some initial
information (for example, assumptions, axioms,
definitions) and applies inference rules (for example,
remembering previous facts, and applying theorems)
to desired conclusions to be concluded. In other
words, constructing proof will occur mainly in a
written format, so that the rules in writing, proof can
be used synonymously with the construction of
proof in a written format.
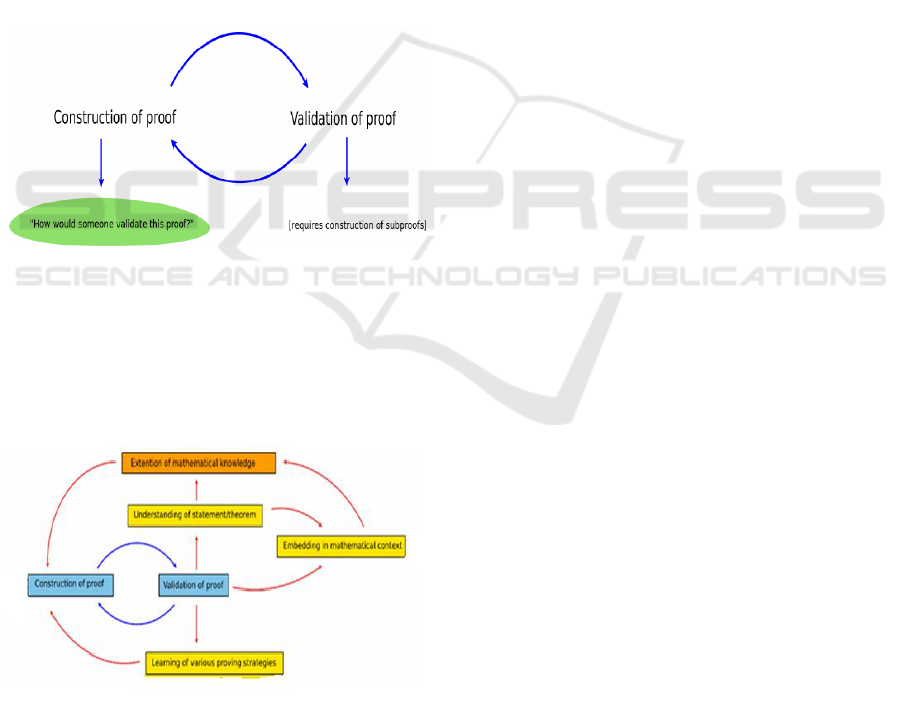
Pfeiffer (2010) states that validation processes
can usually be managed in a linear sequence, such as
constructing proofs. On the other hand the
construction of proof and validation of proof
requires each other, because during the process of
constructing proof, how the proof will be validated,
and as proof validation tends to require the
construction of parts of proof or sub-proofs, this
relationship can be seen in the following diagram:
Figure 1: Construction Related to Proof Validation.
To clarify the link between construction and
proof validation, Pfeiffer developed the diagram
above as a development of the impact of learning
through proof validation, as in the next diagram:
Figure 2: Validation of Proof in the Process of Learning
about Mathematical Proof.
Based on Figure 2, it appears that the link
between validation of proof and construction of
proof, validation of proof requires an understanding
of statements/theorems that are appropriate to the
mathematical context and additional mathematical
knowledge and learning from various strategies for
constructing proof, and vice versa. It is further
expected that the ability to validate proof can
improve the ability to construct proofs, develop a
deeper understanding of the meaning and the
meaning of the theorem that is proven and develop
knowledge, methods or strategies in mathematical
proof.
According to Selden and Selden (2014) three
actions that are useful in constructing proof are: (1)
Exploring. The act of constructing a part of proof,
one may understand what must be proven and what
is available to use without having an idea of how to
proceed. Such a situation, people might try to prove
something new from an unknown value; (2)
Reworking arguments in cases of suspected error or
wrong direction. Constructing proof, perhaps one
should be suspected that someone made a mistake or
made an argument that was not in the direction and
did not help. The thing to do is to re-respond to part
of the argument; (3) Validating a proof of
completion. After completing the proof, we must
read and examine carefully the truth in each row
from top to bottom and each of the following lines
of what has been said above.
The mathematical knowledge related to the
activity of understanding and validating proof and
constructing the proof, carried out by teachers and
students, including the one presented by Rogers and
Steele (2012) is "how to verify the truth" which is
checking or confirming the truth of a known idea,
"explaining why" is opening up the thoughts and
reasons behind why this statement is true including
giving reasons to support the conjecture (Hanna,
1995), "communicating mathematical knowledge"
that is helping others understand mathematical ideas
and disseminating mathematical knowledge to
others, "creating new mathematical knowledge, "He
meant developing new ideas in mathematics,"
confirming conjectures/conjectures ", building
mathematical ideas, and" systematizing domains
"namely applying logical structures to the domain of
mathematics, organizing and cataloging the results
in relation to an axiom and prior knowledge (Knuth,
2002). In line with this, Hanna (Magajna, 2013)
states that the function of proof and proof is
verification that something is true, explanation of
why something is true, systematization of concepts,
variations in results and theorems, discovery of new
Identifying Mathematics Education Studentsâ
˘
A
´
Z Obstacles in Reading and Constructing Proof in Real Analysis Courses
265
results, communication of mathematical knowledge,
constructing theories empirically, exploration of the
meaning of definitions, and incorporation of known
facts into new frameworks.
2 METHOD
Subjects in this study consisted of 43 students of
mathematics education FKIP Khairun University,
and data collected through tests and interviews.
Interviews were conducted on 6 (six) students based
on the work to identify the obstacle experienced in
reading, understanding and constructing a proof. The
data were analyzed by the descriptive-qualitative
approach.
3 RESULTS AND DISCUSSION
Based on the results of the study of the aspects
observed in the mathematical proof ability of
students, namely: (1) The ability to read and
understand the proof, and (2) The ability to construct
proofs, presented several examples of student
answers that have not been perfect in carrying out
proof. Errors that often appear in answering
questions and types of errors from the results of
student answers.
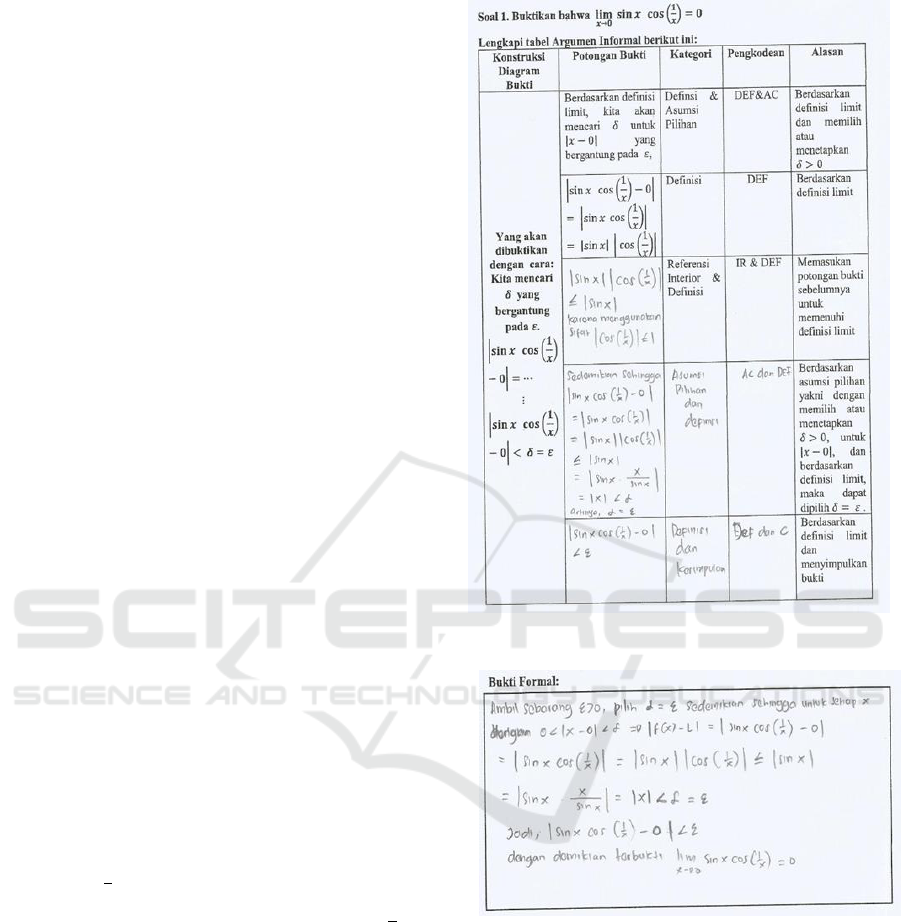
To solve the question no. 1, You are welcome to
read carefully the examples of proof presented
starting from the table of Informal Arguments to
formal proof, then you are asked to prove the matter
in the space provided. If the space provided is not
sufficient in the verification process, you can use the
additional paper provided. In this study, students
were asked to read the given example, "prove that
". Next is given the problem as
follows: Problem 1. Prove that
.
Problem number 1 above relates to the indicator
of the ability to verify the steps in formal proof from
the examples provided to be applied in solving
problems similar to the example. Students are
expected to begin verification by verifying and
completing the informal argument table that has
been provided, which then follows the stages as a
basis for probing the question in question. Errors
made by students, including those presented below:
Figure 3: Results of Student Work in Completing Informal
Arguments.
Figure 4. Example of a Formal Proof Job Preparing
Students to Question 1
The results of student work in Figures 3 and 4
are one example of an incomplete and inappropriate
answer. Before describing the work results of
students, researchers conducted interviews with
students with the aim of uncovering errors or
difficulties encountered in carrying out the
verification of the questions above. The results of
the interview are presented as follows:
ICTL 2018 - The 1st International Conference on Teaching and Learning
266

Researcher: In completing the argument table (3
rd
row of the 2
nd
column), you only use
properties
, but not yet
using properties
, why
not use properties
?
M
Eks-16
: I see in the example only properties
, written by Sir
Researcher: Oh yes, but as soon as you complete
the next column, there appear
properties
, what
underlies you write like that?
M
Eks-16
: When I write like that, I think
with can share one another, Sir
Researcher: If you look at the time you compile a
formal proof, election it's right,
but once compiling the next step
appears
, this step
is illogical, why do this?
M
Eks-16
: After I tried using it … I mean what I
fill in the table of informal arguments,
I think this is correct Sir, it turns out
this is wrong, sir, I have a bit of
difficulty utilizing the traits
and manipulate signs of inequality
sir
Researcher: Ok, thank you, I think you have shown
a persistent effort to do proofs,
hopefully for the next question you are
better.
From the results of the interview, it shows that
the third row of the second column, students have
tried to include the previous pieces of evidence with
categories and coding, but the pieces of evidence in
the form of arguments that have not guaranteed the
next trait, students have not used the properties of
. Then for the next column, students
have used the previous step, but the pieces of
evidence for the choice assumption category (AC)
and (DEF) are ”
”
becomes illogical, even though in the selection δ = ε
as in the column it shows that the student is right to
choose. Next in compiling formal evidence, the
steps in the first row up to the third row of students
have done correctly, by using triangular inequality
and properties
, but in the fourth row the
students repeated, making mistakes entering “
”,so this formal proof
becomes invalid.
In general, from the results of the analysis of
student work for question number 1, several
obstacles can be found which cause student
difficulties in proving, as follows: (1) When
completing the informal argument table, students
cannot yet utilize the general nature of
and
, (2) Make mistakes in selection δ and
manipulate the nature of inequality ≤ to be <
(obstacle to manipulating algebraic forms), (3)
Students have difficulty utilizing the concepts
related to the questions to be proven, and (4)
Students have difficulty connecting informal
arguments and rewriting them into formal proof.
4 CONCLUSIONS
In general, from the results of the analysis of student
work, several obstacles can be found which give rise
to student difficulties in proof, namely when
completing the informal argument table, students
were not able to take advantage of the general nature
of |cos x | ≤ 1, making mistakes in the selection δ do
proof construction into formal proof, manipulate the
nature of inequality ≤ to be (obstacle to
manipulating algebraic forms), students have
difficulty utilizing concepts related to the questions
to be proven, students have difficulty connecting
informal arguments and rewriting them into formal
proof, and in the final settlement in constructing
proofs of students experiencing obstacles in using
the previous steps to formulate formal proof.
REFERENCES
Brousseau, G. 1997. Theory of didactical situations in
mathematics. Dordrecht: Kluwer academic publisher.
Cornu, B. 1991. Limits. In D. Tall (Ed.), Advanced
mathematical thinking. (pp. 153-166). Dordrecht:
Kluwer Academic Publishers.
Dubinsky, E. 1991. Reflective abstraction in advanced
mathematical thinking. In D. Tall (Ed.), Advanced
mathematical thinking (pp. 95-126). Dordrecht:
Kluwer academic publishers.
Hanna, G. 1995. Challenges to the importance of proof.
For the Learning of Mathematics, 15(3), 42–49.
Knuth, E. J. 2002. Secondary school mathematics teachers'
conceptions of proof. Journal for Research in
Mathematics Education, 33(5):379-405.
Magajna, Z. 2013. Overcoming the Obstacle of Poor
Knowledge in Proving Geometry Tasks, Journal
Centre for Educational Policy Studies. 3(4), 99-115.
Identifying Mathematics Education Studentsâ
˘
A
´
Z Obstacles in Reading and Constructing Proof in Real Analysis Courses
267

Moru, K. 2007. Talking with the literature on
epistemological obstacles. For the Learning of
Mathematics, 27(3), 34-37.
Pfeiffer, K. 2010.
The role of proof validation in students'
mathematical learning.
MSOR Connections. Vol 10. No.
2. 17-2.
Rogers & Steele. 2012. Relationships between
mathematical knowledge for teaching and teaching
practice: the case of proof. Journal Math Teacher
Educ, 15, 159–180.
Rosenblant, M.L. 1988. Writing and Reading: The
Transactional Theory. Center for the Study of Reading
(A Reading Research and Education Center Report).
Technical Report No. 416, 1-26. University of Illinois
at Urbana-Champaign.
Selden, A., & Selden, J. 2003. Validations of Proofs
Considered as Texts: Can Undergraduates Tell
Whether an Argument Proves a Theorem?. Journal for
Research in Mathematics Education. 34(1), 4-36.
Selden, A., & Selden, J. 2014. The roles of behavioral
schemas, persistence, and self-efficacy in proof
construction. In B. Ubuz, C. Hasar, & M. A. Mariotti
(Eds.). Proceedings of the Eighth Congress of the
European Society for Research in Mathematics
Education [CERME8] (pp. 246-255). Ankara, Turkey:
Middle East Technical University.
Sfard, A. 1991. On the dual nature of mathematical
conceptions: Reflections on processes and objects as
different sides of the same coin. Educational Studies
in Mathematics, 22(1), 1-36.
Sierpinska, A. 1987. Humanities students and
epistemological obstacles related to limits.
Educational Studies in Mathematics, 18(4), 371-397.
Tall, D., & Vinner, S. 1981. Concept image and concept
definition in mathematics with particular reference to
limits and continuity. Educational Studies in
Mathematics, 12(2), 258-276.
Tall, D. 1991. Reflections. In D. Tall (Ed.), Advanced
mathematical thinking (pp. 3-24). Dordrecht: Kluwer.
ICTL 2018 - The 1st International Conference on Teaching and Learning
268
