Boundedness in Finite Dimensional -Normed Spaces
Esih Sukaesih
UIN Sunan Gunung Djati Bandung, Jl. A. H. Nasution no. 105, Bandung, Indonesia
Keywords: Finite Dimensional Spaces, -Normed Spaces.
Abstract: Sukaesih and Gunawan, in 2016, shown relation of bounded set in -normed spaces through the equivalence
of norm and -norm. In this paper, the relation of boundedness with respect to linearly independent vectors
() are shown by the relation of linearly independent sets.
1 INTRODUCTION
Gähler was introduced 2-normed spaces, in 1964. The
generalization to -normed spaces also done by
Gähler (Gähler , 1969). An -norm is a real function
which satisfies the following
conditions for all
and for any ,
if and only if
linearly dependent,
is invariant under permutation,
for every
,
.
The pair
is called an -normed
space.
In 2011, Harikrishnan and Ravindra introduced
the definition of bounded set in 2-normed spaces. It
was than generalized to definition of bounded set in
-normed spaces by Kir and Kiziltunc (Kir and
Kiziltunc, 2014). But, Gunawan et.al. (Gunawan
et.al., 2016) found lack of the Kir and Kiziltunc’s
definition, they then defined new definition of
bounded set in -normed spaces.
Definition 1: (Sukaesih, 2017) Let (
) be an
-normed space, be a nonempty subset of and
be a linearly independent set
. Then is called bounded with respect to if there
is such that
for every and for every
.
Let
be a collection of bounded
set with respect to . If a set is bounded with
respect to , then
.
Hereafter, let () be a finite
dimensional -normed space (dim()), be a
nonempty set of , and
be a
linearly independent vectors in (rank
),
where .
Sukaesih and Gunawan (Sukaesih and Gunawan,
2016) shown the relation of boundedness with respect
to any linearly independent sets.
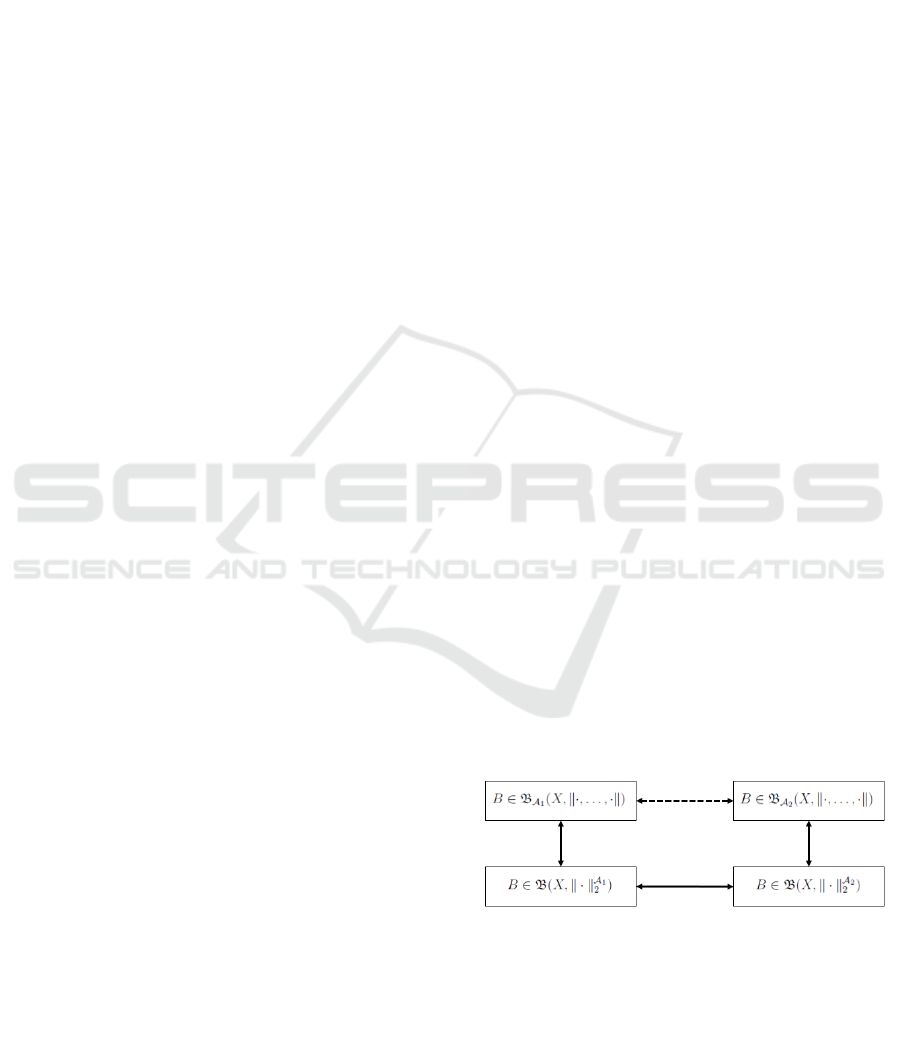
Lemma 2: (Sukaesih and Gunawan, 2016) Let
be a finite dimensional -normed space, be
a nonempty set of . If
be a
linearly independent set in (
)
and
be a linearly independent
set in (
) then a set
is bounded with respect to
if and only if is
bounded with respect to
.
Figure 1: The relation between the boundedness with
respect to
and the boundedness with respect to
.
Lemma 2 was proven by following Corollary and
equivalencies in normed spaces.
Corollary 3: (Sukaesih and Gunawan, 2016)
Let be a finite dimensional -normed
420
Sukaesih, E.
Boundedness in Finite Dimensional n-Normed Spaces.
DOI: 10.5220/0008522904200422
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 420-422
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

space (dim()) which also equipped with a norm
, be a nonempty set of . If
be a linearly independent set in then a set is
bounded with respect to if and only if is bounded
in (
).
Let
be collection of bounded set in
. If a set is bounded in
, then
. Further on norm
could be
studied in (Burhan, 2011).
2 MAIN RESULT
In an -normed space , we have many
sets of linearly independent vectors in (
). Here some relation of boundedness in finite
dimensional -normed spaces.
Theorem 4: Let be a finite dimensional
-normed space (dim()) and
,
be linearly
independent sets in that
and
. If a set is bounded with
respect to
, then is bounded set with respect to
.
Proof: Because of the boundedness with respect to
then we have
for every
and for every
.
Because of
then we have
, such that
with
for
, ,
and for every
.
A vector space can be generated by many linearly
independent sets. If two linearly independent sets
generated the same space, then the boundedness with
respect to a linearly independent set tie up the
boundedness with respect to another linearly
independent set. Then Lemma 2 was generalized for
any with .
Lemma 5: Let be a finite dimensional
-normed space (dim()) and
,
be linearly independent sets in
such that
and .
A set is bounded with repect to
if and only if a
set is bounded with respect to
.
Proof. From the boundedness with respect to
,
we have
for every and
for every
. Since
then we have
, such that
,
with
for
, ,
and for every
.
Conversely, use the same way.
Figure 2: The relation between any two linearly
independent set that generated the same space.
For
and
are basis of , we have the
following condition.
Boundedness in Finite Dimensional n-Normed Spaces
421

Corollary 6: Let be a finite dimensional
-normed space (dim()) and
,
be basis on
. A set is bounded with repect to
if and only if
set is bounded with respect to
.
Proof. Use Lemma 5 for
and
are basis of .
REFERENCES
Burhan, M. J. I. 2011. Teorema Titik Tetap di Ruang Norm-
Berdimensi Hingga, Master thesis, Institut Teknologi
Bandung.
Gähler, S. 1964. Lineare 2-normierte Räume, Math. Nachr,
28.
Gähler, S. 1969, Untersuchungen Uber Verallgemeinerte
m-Metrische Räume I, Math. Nachr.
Gähler, S. 1969, Untersuchungen Uber Verallgemeinerte
m-Metrische Räume II, Math. Nachr.
Gunawan, H., Neswan, O., and Sukaesih, E. 2015. Fixed
point theorems on bounded sets in an -normed spaces,
JMA, 6(3), pp.51-58.
Harikrishnan, P., Ravindran, K. 2011. Some properties of
Accretive operators in linear 2-normed spaces, Int.
Math. Forum, 6(59).
Kir, M., and Kiziltunc, H. 2014. On fixed point theorems
for contraction mappings in -normed spaces, Applied
Math. Information Sci. Letters, 2.
Sukaesih, E. and Gunawan, H. 2016. Bounded sets in finite
dimensional -normed spaces, Proceeding IICMA
2015.
Sukaesih, E. 2017. Contractive mapping theorems in
bounded sets in -normed spaces, Doctoral
Dissertation, Institut Teknologi Bandung.
ICMIs 2018 - International Conference on Mathematics and Islam
422
