Source Problem Answered False in Analogical Reasoning: Why

Students Do It?

Kristayulita

, Toto Nusantara

, Abdur Rahman As’ari

and Cholis Sa’dijah

Jurusan Tadris Matematika, Universitas Islam Negeri Mataram, Jln Pendidikan No.35 Mataram,

Nusa Tenggara Barat, Indonesia

Department of Mathematics, University of Malang, Jln Semarang 5 Malang, Jawa Timur, Indonesia

Keywords: Source Problem, False, Analogical Reasoning.

Abstract: The purpose of this study was to describe thinking processes students' in answer source problem is false and

answer target problem is true. Two analogical problems, the students will solve two problems using the same

procedure and have two possible answers are both is true or false. Using qualitative design approach, the study

was conducted at Universitas Negeri Malang, Indonesia. The instrument used probability problems topic in

conjunction with independent events. The findings of this study showed that the presence of misconceptions

and errors occur in solving the problem source. Factor time can affect and there is a time lag in solving-

problem of both analogical problems. Furthermore, target problem is answered correctly because the student

has time to reflect on the answer to the source problem and the student improves working memory to recall

the previous learning experience.

1 INTRODUCTION

Analogical reasoning is an essential ability of human

cognition since analogies can be used to explain many

aspects of cognitive creativity, productivity, and

adaptivity. In addition, analogical reasoning is central

to the learning of abstract, procedural, and

mathematical ideas (Magdas 2015). Magdas (2015)

adds that analogical reasoning can develop potential

such as the skill of discovering similar things that are

already known for new situations, skills to apply

something already known for something new, and

generalizability skills.

English (2004) said that solving the analogical

problem can improve students' mathematical

conceptual knowledge. This is reinforced by Amir-

Mofidi, Amiripour, and Bijan-Zadeh (2012), by

facilitating students via analogical reasoning can help

students to connect new mathematical knowledge to

existing knowledge, learn more about math, and math

concepts in long-term memory. Alexander and Buehl

(2004) found evidence that there is a relationship

between analytical reasoning abilities and students'

mathematical abilities in their research.

If students can do all the stages in analogical

reasoning, then students can learn math more deeply

and the mathematical concept can be stored in long-

term memory (Amir-Mofidi, Amiripour, and Bijan-

Zadeh, 2012). The analogical reasoning makes the

student must find the relationship of source problems

with target problems and relate to the relevant

mathematical concepts (Pang and Dindyal, 2009).

Therefore, students must have a strong understanding

of concepts and have the skills to connect old

knowledge and new knowledge (May, 2009).

Problem-solving using analogical reasoning can

provide many benefits. Bernardo (2001) explains that

analogical reasoning can allow students to explore

and engage in searching for mathematical

information that can lead students to a deeper level of

understanding. Analogical reasoning is important

because students must make their own discoveries,

discoveries made can help students to build an

understanding of new information (Bal-Sezerel and

Sak 2013). In addition, students should also establish

relationships between analogical problems and

improve students' ability from routine problem

solving to advance troubleshooting.

Chuang and She (2013a) said that analogical

reasoning can develop understanding, solve

problems, and conduct investigations. In solving the

problem students are asked to understand the

relationship between target problems and source

362

Kristayulita, ., Nusantara, T., As’ari, A. and Sa’dijah, C.

Source Problem Answered False in Analogical Reasoning: Why Students Do it?.

DOI: 10.5220/0008522003620368

In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 362-368

ISBN: 978-989-758-407-7

problems so that the student in analogical reasoning

is required to investigate activity. Students' ability to

investigate analogous similarities differed by the pre-

requisites of students (Holyoak, 2012).

The analogical problem consists of source

problems and target problems. The existence of

source problems and target problems on analogical

reasoning requires students to look for similar

structural relationships of similar properties so that

students can solve the given target problem. So

analogical reasoning provides basic cognitive tools so

that students can use the new phenomenon approach

and transfer the entire context (Richland, Morrison,

and Holyoak, 2006). Analogical problems are

expected to help students understand in solving

mathematical problems. This is because analogical

reasoning train students to develop problem-solving

skills (Chuang and She 2013b).

English (1999) said that source problem has

characteristics: (1) given before the target problem,

(2) problem is easy, and (3) can help resolve target

problem or as initial knowledge of the target problem.

And then target problem has characteristics: (1)

source problem that are modified or expanded, (2) the

structure of the target problem related to the structure

of the source problem, and (3) problem is complex. In

this study using analogical problem were the target

problem is the source problem of the modified.

The concept of work in solving analogical

problem consisting of source problems and target

problems are (1) the source problem is done first

correctly, (2) then work on the target problem, (3)

with students' knowledge, through analogy reasoning

will look for similarities between source problems

and target problems, and (4) the results of the

conclusions summarized as the basis for solving

target problems. Assmus, Forster, and Fritzlar (2014)

explains there are 4 types of answers to two

analogical problems are (1) the source problem and

the target problem are answered correctly, (2) the

source problem is answered correctly and the target

problem is answered incorrectly, (3) the source

problem is answered incorrectly and the target

problem is answered correctly, and (4) the source

problem and the target problem are answered

incorrectly.

In this study will be discussed about student cannot

solve the given source problem, but the target

problem is solved correctly. Further this research

focuses on:

1. Why do students answer source problems

incorrect and then target problems correct?

2. What causes students to answer the source

problem is incorrect while the target problem

is correct?

2 METHOD

2.1 Research Design

The first, this study apply the descriptive quantitative

for to see percentages of student answer criteria. The

second, this study apply the descriptive qualitative

approach for to see thinking process of students.

Following are the description of the method used in

this study. Creswell (2014), such research is a

qualitative research. One of the characteristics of

qualitative research is that the process of research is

always evolving dynamically. All the stages of the

research process can change after the researchers

enter the field and start collecting data. For example,

the individuals studied and the locations visited can

also change at any time (Creswell, 2013).

2.2 Research Subject

The subjects are 33 semester V students at

Universitas Negeri Malang, Indonesia. All Students

have not completed the theory of probability learning

in the Mathematical Statistics course.

2.3 Research Instrument

The analogical problem consists of source problems

and target problems. Source problems and target

problems are related to conjunction with independent

two events problems. Source problems and target

problems has the same resolution procedure.

Analogical problems in this study can be seen in

Table 1.

2.4 Research Procedure

Research is done in several stages. Stages include

preparation, execution, analysis of results, and

interviews.

2.4.1 Preparation

a) Subjects are given instructions to work on the

problem individually.

b) Subjects are asked to carefully read the

instructions and answer questions about

resolving an analogical problem related to

Source Problem Answered False in Analogical Reasoning: Why Students Do it?

363

conjunction with independent two events

problem.

Table1: Conjunction with independent events problems.

Type

Question

Source

Problem

There are 76 books in the Science section of

the library, six of which are new. In the

History section, there are 120 books, 15 of

which are new. The principal randomly picks

a book from each of the two sections. What

is the probability that the principal picks a

new from both sections?

Target

Problem

There are 24 schools in District A, eight of

which are public school. In District B, there

are 32 schools, 12 of which are public

school. For each district, a school is

randomly chosen to host the district sports

fest. What is the probability that a public

school is chosen to the host fest in both

district?

(Bernardo 2001).

2.4.2 Implementation

a) Subjects are given 45 minutes to work on

resource issues related to conjunction with

independent two events problem.

b) Response results of source problems were

collected.

c) After 45 minutes, subjects were given 45

minutes to work on target problems in

conjunction with independent two events.

d) Results of answers to target problems are

collected.

2.4.3 Analysis of Results

a) The result of the subject's answers to source

problems and target problems analyzed.

b) Categorize the results of the subject's answer

analysis of source problems and target

problem.

2.4.4 Unstructured Interviews

a) Conduct interviews on subjects who

answered source problem are false and

answered target problem is true.

b) Describe analogical reasoning schema that

occurs on the subject.

3 RESULTS

Based on description quantitative analysis obtained

the following research results. There are 33 students

who participated in this study. Each student is given

two problems that must be done, namely source

problems (the first problem) and target problems (the

second problem). Source problem given at the

beginning was followed by providing a target

problem. Source problem is accomplished in for 37

minutes. By an interval of 45 minutes, the student is

given the target problem. For target problems, the

students work for a period of approximately 15

minutes. From the student's answers, there are several

mistakes made by the students.

In aggregate, approximately 69.69% have wrong

answers on an analogical problem. The number of

students to answer one of the first problems (source

problems) was approximately 57.57%, while the

second problem (target problems) was approximately

48.48% of the students. There are four criteria

students answered are (1) the student who answer

source problems and target problems are correct, (2)

the student who answers source problems and target

problems are wrong, (3) the student who answers

source problems is correct and target problems is

wrong, and (4) the student answers source problems

is wrong and target problem is correct (can be seen in

Table 2).

Furthermore, the description of qualitative

analysis obtained from the following studies.

Researches describe the thinking of student’s eligible

source problems were answered incorrectly and target

problems were answered correctly.

Table 2: Data result of answer analogical problem.

Description

Total

students

(%)

Source problems and target

problems were answered correctly

30.3

Source problems and target

problems were answered

incorrectly

36.36

Source problems were answered

incorrectly and target problems

were answered correctly.

21.21

Source Problems were answered

correctly and target problems were

answered incorrectly.

12.12

Total

100

Based on Figure 1 (a) and 1 (b), subject S1 begins

by identifying what is known from the source

problem. Subject S1 wrote probability taken new

ICMIs 2018 - International Conference on Mathematics and Islam

364

science books

and probability taken new history

books is

120

. Then the subject S1 determines the

probability of taking a new book from the science and

history section by summing up the probability of new

science books and the chances of a new history book

acquired

152

. S1 subject answers wrong source

problem. Next, S1 completes the target problem.

Subject S1 do mapping process from target problem

to source problem. Furthermore, in the structuring

process, subject S1 identifies the problem as it did in

resolving the source problem. The subject S1

identifies the target problem by stating that the

selected probability of public school in area A is

and region B is

. In the applying process, subject S1

solves the target problem of determining the

eligibility of public schools from both regions by

multiplying the selected probability of public schools

in area A and the selected probability of public school

in region B is obtained

. The target troubleshooting

process is not the same as resolving the source

problem. In the verifying process, the answer to the

target problem is similar to the result of the source

problem answer. The answer to the target problem is

Figure 1 (a) & 1 (b): Answers to source problems and target

problems subject S1.

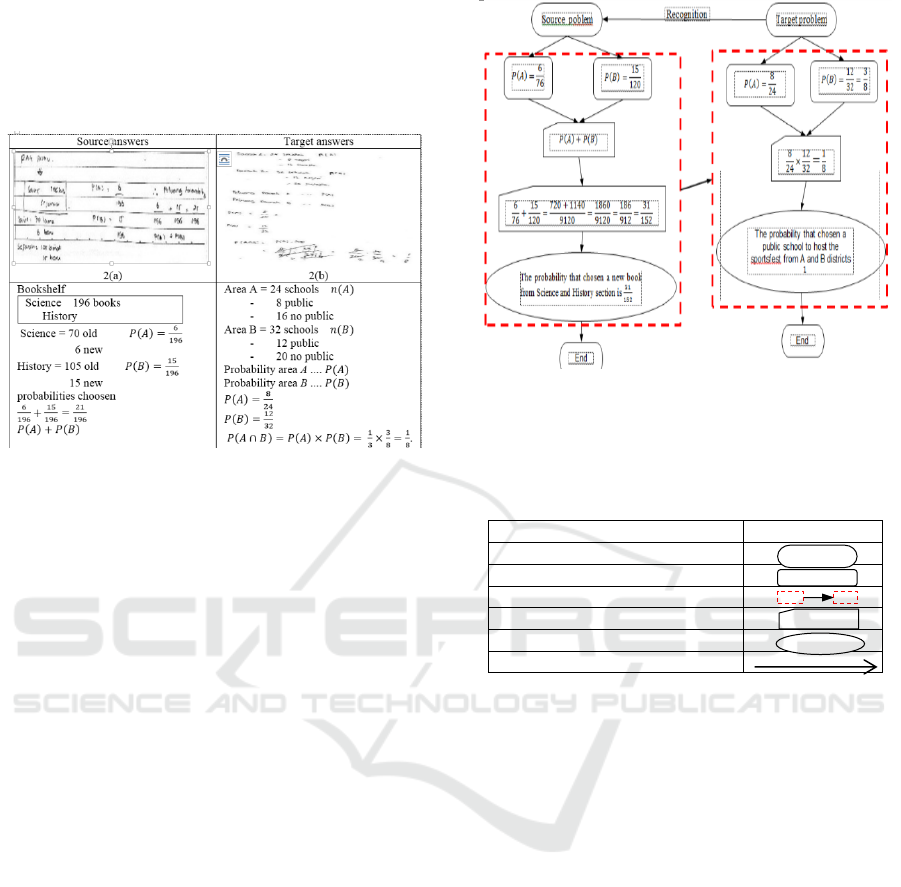
Subject S2 answered source problems by

summing the books of science and the history of 196

books. And then subject S2 determining probabilities

of each new science books and new history books

acquired

196

and

196

. Furthermore, subject S2

determine probability of new books chosen from

science and history by summing up probabilities of a

new science book and a new book of history, so that

it gets

196

The following is interview expert S2.

I: What do you think about the current look (pointing

at the source problem)?

S2: Here the book because ... there are 76 science

sections and there are 6 new ... and there is 120 books

section of history... then there is the new 15. What

being asked is how many probabilities of fetching

new book science and history. Well Here I suppose

that science n(A) and the history of n(B). Probability

science P(A) and a historical probability P(B). It's

bookshelves right. It's not a science bookshelf

bookcase but also history. But one shelf was a book

of science and history... the total of science and

historical books on the shows is 196 books. So, the

contents of the shelves of science and history books

then S2 is mastered how many probabilities right here

chose a new book of science and history... It means

that we take his place not just science but also science

and history with the total number of 196. Because of

the requested new book, the probabilities for science

is 𝑃(𝐴) =

196

and the historical probability is 𝑃(𝐵) =

196

I: What do you know about this matter? (pointing at

the target problem)

S2: similar to the previous example (refer to the

source problem) ... there are two local schools which

are area A and area B. Area A has 24 schools and 8

public schools ... and other, there are 32 schools, there

are 12 public schools. The probability of choosing

public schools in area A is 𝑃(𝐴) =

and the

probability to choose public schools in area B is

𝑃(𝐵) =

I: how many answers about this (pointing at the

source problem)?

S2: As the requested probability of drawing a new

book of science and history then probability is

summed, so 𝑃(𝐴) + 𝑃(𝐵) =

196

I: how to answer this question? (pointing at the target

problem)

S2: because the matter is related to the two events

are independent ... then the probabilities are drawn by

the public schools of the two regions by multiplying

the probability of events A and B that gained

Based on the subject's answer in this study: the

first, the subject resolves the source problem via

identifying the problem correctly. However, subject

recognizes mathematical formulas incorrectly. Then,

subject applies mathematical formulas and obtains

incorrect results. The second, subject resolves target

problem identifying the problem. The subject

Source Problem Answered False in Analogical Reasoning: Why Students Do it?

365

recognizes mathematical formulas correctly. The

mathematical formula used between the source

problem and the target problem is different. Then, the

subject applies mathematical formulas and gets the

correct results.

Figure 2: (a) & 2 (b): Answers to source problems and target

problems subject S2.

Analogical problem-solving begins by

recognizing the similarity between the target problem

and the source problem. Then, they mapped the target

problem to the source problem. Source

troubleshooting steps are mapped one-to-one to

troubleshooting steps that begin with the setup,

deployment, and verification process. The problem-

solving process analogies between the target problem

and the source problem using the analogical

reasoning stage can be seen in Figure 3.

Description of the encoding in analogical

reasoning process of the student in solving-problem

the probability of two independent events on Figure 3

can be seen on Table 3.

4 DISCUSSION

Analogical problem consists of source problems and

target problems. First, students solve source problems

and then solve the target problems. The second,

problems are analogy then source problems were

answered correctly, it can be ascertained target

problems were answered correctly. Pang and Dindyal

(2009) students must search for a common connection

between source problems and target problems so that

students can use mathematical concepts from source

problems to solve target problems.

Figure 3: Analogical reasoning process of the student in

solving-problem the probability of two independent events.

Table 3: Description of the encoding in analogical

reasoning process of the student in solving-problem the

probability of two independent events.

Term

Code

Start/End

Structuring

Mapping

Applying

Verifying

Process Activity

But the existing theory does not apply to this case.

The student did not solve source problems correctly,

but the target problems were resolved correctly.

Basically, students understand ways to answer source

problems and target problems. However, students do

not use the same mathematical concepts to solve an

analogical problem. But perceptions of students to

problem solving on both analogical problems is the

same. The concept and context of the given problem

have something in common. So students are expected

to transfer the entire context with existing cognitive

tools through analogical reasoning(Richland,

Holyoak, and Stigler, 2004).

There are two ways in which students solve source

problems. First, students summing science and

history books, summing new books from science and

history and determine probabilities of a new book

from science books and history books. The second,

students determine probabilities of new science

books, students determine probabilities of new

history books, and determine probabilities of a new

book from science books and history books. The first

way, students assume that should add up all the books

from the science and history, and new books on

ICMIs 2018 - International Conference on Mathematics and Islam

366

science and history because the books are stored on a

shelf in the library. Students misconception in

resolving source problems because students do not

understand the problem well, the concept is wrong,

and the procedure is wrong (Sandhu, 2013; Sarwadi

and Shahrill, 2014). While the second way, the

students determine each probability chosen new

books from science and history section. Then

determine probabilities of a new book from the

science and history. However, the formula used is

wrong in determining probabilities of a new book

from science and history section. This can mean that

students make mistakes because students understand

the problem well, but either incorrect or incorrect

formula in writing the operation marks used (Sandhu,

2013; Lin et al., 2012). Furthermore, the mistake

made is a transformation error that is an error in using

the formula correctly (White, 2005; Saleh, Yuwono,

As’ari, 2017).

One of the factors that this happens is structuring.

Students can't students cannot perform structuring the

source problem correctly, students cannot see key

word in the source problem, and students cannot find

a relationship between the target problems with the

source problem. There are reading errors,

comprehension errors, and transformation errors

(Saleh, Yuwono, As’ ari, et al. 2017). Kristayulita,

Nusantara, and As'ari (2018) said that these errors are

structuring errors. Ruppert (2013) said that

identifying each mathematical object that exists in the

source problem with the coding of attributes or

characteristics and making conclusions from

relationships that are identical between the problem

source and the target problem. Furthermore, students

are not using mathematical formulas properly for

source problem. Mathematical formulas used

between source problem and target problem are

different. There is skill process errors (Saleh,

Yuwono, As’ari, et al. 2017). Kristayulita, Nusantara,

and As'ari (2018) said that these errors are applying

errors. This is influenced by learning experiences and

prior knowledge from students. Novick (1988) said

that we are often reminded of similar problems solved

earlier and may use the solution procedure from an

old problem to solve a new one, such analogical

transfer. Besides, time is the other factor. There is an

interval of 45 minutes before the students to solve

target problems. The length of time students have

after solving source problems with time before

completing target problems, students can use to

reflect the answer to source problems obtained. So,

the students try hard to solve target problems

correctly.

All students have a presumption that source

problem and target problem is analogy. Students

solve target problems using the same concepts and

procedures by solving source problems. Students use

analogy reasoning to solve target problems. Amir-

Mofidi, Amiripour, and Bijan-Zadeh (2012) by

facilitating students to analogical reasoning can help

students to connect new mathematical knowledge to

existing knowledge, learn more in-depth math, and

math concepts can be stored in long-term memory. So

that the student changes, the formula used is no longer

the same as solving source problems. However,

students use concepts and procedures appropriate to

the problem. In addition to the time factor, early

knowledge of long-term students stored in long-term

memory can be recalled. Source problems are a

trigger to call the memory deeper to solve target

problems. We hope you find the information in this

template useful in the preparation of your submission.

5 CONCLUSIONS

The results show that there are misconceptions and

errors made by students in solving source problems.

Even if the source problem is answered wrongly with

the analogical reasoning students can solve the target

problem by paying attention to the previous learning

experience. Target problem can be answered

correctly due to the time and working memory.

Students' prior knowledge stored in long-term

memory is recalled by connecting experience in

solving the problem source.

Further research needs to look at the level of

intelligence of students who do so. In addition, based

on student learning styles need to be researched and

analysis further. Teachers need to learn by displaying

analogical problems aimed at improving students'

understanding of the math material being taught.

We hope you find the information in this template

useful in the preparation of your submission.

ACKNOWLEDGEMENTS

The author is thankful to lecture who helps in

providing classes for retrieving data; and to the

researchers who shared there their valuable results,

without which this study would not have been

possible; to semester V students at Universitas Negeri

Malang, Indonesia for participation as respondents in

retrieving data; to ARA, TN, & CS editing this

paper’s text.

Source Problem Answered False in Analogical Reasoning: Why Students Do it?

367

REFERENCES

Alexander, Patricia A., and Michelle M. Buehl, 2004.

Seeing the Possibilities: Constructing and Validating

Measures of Mathematical and Analogical Reasoning

for Young Children. Mathematical and Analogical

Reasoning of Young Learners, 23–45.

Amir-Mofidi, Somayeh, Parvaneh Amiripour, and

Mohammad H. Bijan-Zadeh, 2012. Instruction of

Mathematical Concepts through Analogical Reasoning

Skills. Indian Journal of Science and Technology 5 (6):

2916–2922.

Assmus, Daniela, F. Forster, and Torsten Fritzlar, 2014.

Analogizing during Mathematical Problem Solving-

Theoretical and Empirical Considerations. In

Proceeding of the Joint Meeting of PME, 38:73–80,

https://iris.unito.it/retrieve/handle/2318/1620514/2854

55/PME38-2014%20Vancouver%202.pdf#page=83.

Bal-Sezerel, Bilge, and Ugur Sak. 2013. The Selective

Problem-Solving Model (SPS) and Its Social Validity

in Solving Mathematical Problems. The International

Journal of Creativity and Problem Solving 23 (1): 71–

87.

Bernardo, Allan B. I., 2001. Analogical Problem

Construction and Transfer in Mathematical Problem

Solving. Educational Psychology 21 (2): 137–50,

https://doi.org/10.1080/01443410020043841.

Chuang, Ming-Hua, and Hsiao-Ching She, 2013a, fostering

5th Grade Students’ Understanding of Science via

Salience Analogical Reasoning in On-Line and

Classroom Learning Environments. Educational

Technology & Society 16 (3): 102–118.

———, 2013b. Fostering 5th Grade Students’

Understanding of Science via Salience Analogical

Reasoning in On-Line and Classroom Learning

Environments. Educational Technology & Society

16(3): 102–118.

Creswell, John W. 2013. Research Design: Qualitative,

Quantitative, and Mixed Methods Approaches. Sage

publications.

English, Ley D., 1999. Reasoning by Analogy: A

Fundamental Process in Children’s Mathematical

Learning. Developing Mathematical Reasoning in

Grades K-12. Developing Mathematical Reasoning in

Grades K-12, 22–36.

English, Lyn D., 2004. Mathematical and Analogical

Reasoning of Young Learners. Routledge.

Gust, Helmar, and Kai-Uwe Kuhnberger, 2006.

“Explaining Effective Learning by Analogical

Reasoning.” In Proceedings of the Cognitive Science

Society. Vol. 28.

Holyoak, Keith J., 2012. Analogy and Relational

Reasoning. The Oxford Handbook of Thinking and

Reasoning, 234–259.

Kristayulita, K., T. Nusantara, A. R. As’ari, and C.

Sa’dijah, 2018. Identification of Students Errors in

Solving Indirect Analogical Problems Based on

Analogical Reasoning Components. In Journal of

Physics: Conference Series, 1028:012154. IOP

Publishing.

Lin, Tzu-Jung, Richard C. Anderson, John E. Hummel,

May Jadallah, Brian W. Miller, Kim Nguyen-Jahiel,

Joshua A. Morris, Li-Jen Kuo, Il-Hee Kim, and

Xiaoying Wu., 2012. Children’s Use of Analogy during

Collaborative Reasoning. Child Development 83 (4):

1429–1443.

Magdas, Ioana. 2015. Analogical Reasoning in Geometry

Education. Acta Didactica Napocensia 8 (1): 57–65.

May, Mike, 2009. Sensation and Perception. Infobase

Publishing.

Novick, Laura R., 1988. Analogical Transfer, Problem

Similarity, and Expertise. Journal of Experimental

Psychology: Learning, Memory, and Cognition 14 (3):

510.

Pang, Alwyn Wai-Kit, and Jaguthsing Dindyal, 2009.

Analogical Reasoning Errors in Mathematics at Junior

College Level. https://repository.nie.edu.sg/

handle/10497/17789.

Richland, Lindsey E., Keith J. Holyoak, and James W.

Stigler, 2004. Analogy Use in Eighth-Grade

Mathematics Classrooms. Cognition and Instruction 22

(1): 37–60.

Richland, Lindsey E., Robert G. Morrison, and Keith J.

Holyoak, 2006. Children’s Development of Analogical

Reasoning: Insights from Scene Analogy Problems.

Journal of Experimental Child Psychology 94 (3): 249–

273.

Ruppert, Markus, 2013. Ways of Analogical Reasoning-

Thought Processes in an Example Based Learning

Environment. In Eighth Congress of European

Research in Mathematics Education (CERME 8), 6–10.

Saleh, Kristayulita, Ipung Yuwono, Abdur Rahman As’ ari,

and Cholis Sa’dijah, 2017. Errors Analysis Solving

Problems Analogies by Newman Procedure Using

Analogical Reasoning. International Journal of

Humanities and Social Sciences 9 (1).

Saleh, Kristayulita, Ipung Yuwono, Abdur Rahman As’ari,

and Cholis Sa’dijah, 2017. Errors Analysis Solving

Problems Analogies by Newman Procedure Using

Analogical Reasoning. International Journal of

Humanities and Social Sciences 9 (1).

http://www.ijhss.net/index.php/ijhss/article/view/253.

Sandhu, D., 2013. Does Anyone Have Any Information on

the Differences between Misconceptions and Errors in

Mathematics. Research Gate, Online, Retrieved from

Http://www.Researchgate.Net/Post/Does_anyone_hav

e_any_information_on_the_diffErences_between_misc

onceptions_and_errors_in_mathematics), accessed on

March 6, 2016.

Sarwadi, H. R. H., and Masitah Shahrill, 2014.

Understanding Students’ Mathematical Errors and

Misconceptions: The Case of Year 11 Repeating

Students. Mathematics Education Trends and Research

2014: 1–10.

White, Allan L., 2005. Active Mathematics in Classrooms:

Finding out Why Children Make Mistakes-and Then

Doing Something to Help Them. Square One 15 (4):

15–19.

ICMIs 2018 - International Conference on Mathematics and Islam

368