
The Partition Dimension of Bridge Graphs from Homogeneous
Caterpillars and Cycle
Amrullah, Syahrul A., Harry S., M. Turmuzi and M. Anwar, Y. S.
Department of Mathematics Education, Faculty of Teacher Training and Education, Mataram University,
Jl. Majapahit 62 Mataram, Indonesia
Keywords: Partition Dimension, Resolving Partition, Bridge Graph, Caterpillar.
Abstract: The partition dimension of graph is one of open problem in the graph theory. Investigation of the problem can
be solved by operations of graph. Several operations that are known is the partition dimension of corona
product, cartesian product, subdivision operation. In this paper, the partition dimension is investigated by a
bridge operation. Let
,
be two connected graphs and let
and
. The Bridge graph,
is a graph which obtained from two graphs
,
with a linking to . This paper is devoted
to find the partition dimension of the bridge graph from homogeneous caterpillars and the cycle graphs.
1 INTRODUCTION
On the transport network, there is always one path as
the main road. On the main road, there will be several
paths as branch roads. The design of the main path
with a number of intersections originating from the
main road in graph theory is known as caterpillar
graph. In the caterpillar graph, the main path is known
as the backbone edge and the paths of an intersection
are called the leaves edges. In addition to the
transportation path, the graph can be used to design a
robot navigation network (B. Shanmukha et al. 2002,
S. Khuller et al., 1996).
The interesting problem in graph theory which is
an open problem until now is a partition dimension of
the graph. The problem of partition dimension is the
problem to determine the classes of vertices such that
each vertex is distinguished from each other. The
researchers in dimensional partitions used in various
methods namely research in the certain classes of the
graph, or the operations of graphs. Some operations
which were used are corona (Yero et al, 2011),
subdivision (Amrullah et al., 2013, Amrullah et al.,
2015) and cartesian operations (Yero et al., 2010).
One of the operations that have not yet appeared in
partition dimension research is a bridge operation.
2 BASIC CONCEPTS
First, we introduce several notations and basic
concepts to investigate the partition dimension. Let
be a connected graph, . The
distance from vertex to vertex is the
length of a shortest path between and . Let
be a subset of , Then the
distance from a vertex to is
min
. Let
be a
k-partition of . The representation of
vertex with respect to is the vector
. The partition is
called a resolving partition of if
for all distinct . The partition dimension
of , denoted by , is the cardinality of a
minimum resolving partition of . If two vertices
and are in the same partition class under , then we
write
, otherwise
. If
for some , then we shall say that
and are distinguished by
i
L
or and are
distinguishable. Let
i
vL
, if
( , ) 1
i
d v L
for any
ji
LL
then is called a dominant vertex under .
Let
be a partition class distinguishing two vertices
where . Vertices and in
are called
the distance defining vertices of and in
if
,
and
.
Amrullah, ., A., S., S., H., Turmuzi, M. and Y. S., A.
The Partition Dimension of Br idge Graphs from Homogeneous Caterpillars and Cycle.
DOI: 10.5220/0008519602170221
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 217-221
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
217
Let
,
be two connected graphs,
and
. The bridged graph of
and
by
,
, is a graph obtained from
graph
and
which linking the vertex in
to the vertex in
. In this paper, we examine the
bridge graphs
where
is the
homogeneous caterpillar dan
is a cycle graph. The
Homogeneous caterpillar, , is a graph
obtained by attaching
leaves to each
vertex
of the path
, for . The cycle
graph,
,
is a connected graph which each vertex has
one degree with
. This paper
is devoted to find the partition dimension of
where
is a cycle graph.
In the following lemmas, we introduce several
properties which are useful in this research. Lemma
2.1 and Corollary 2.2 are given by G. Chartrand et al.,
(2000).
Lemma 2.1. (G. Chartrand et al., 2000) Let be a
connected with a resolving partition Π. If
for all , then vertices
must be in distinct partition classes of Π.
A lower bound of partition dimension of graph
given by a direct consequence of Lemma 2.1
Corollary 2.2. (G. Chartrand et al., 2000) Let be a
connected graph, if has a vertex having leaves
then .
The next Lemma 2.2 gives the partition
dimension of path
(G. Chartrand et al., 1998)
Lemma 2.2. (G. Chartrand, et al. 1998) Let be a
connected graph of order . Then
if and only if
.
The Lemma 2.2 shows that the other graphs have the
partition dimension at least three.
A homogeneous caterpillar is a graph
obtained by attaching vertices to each vertex
of
the path
, for
. All vertices of degree one
are called leaves. All leaves attached to v
i
are labelled
by
Darmaji et al. (2009) gave the
partition dimension of a homogeneous caterpillar in
the following theorem.
Theorem 2.1 Let be a homogeneous
caterpillar with , . Then,
.
3 MAIN RESULTS
In first result, we give partition dimension of bridge
graph obtaining from a homogeneous caterpillar
C(m,n) for m
{1,2} and cycle C
3
.
Lemma 3.1. If
and
,
, , and ,
, then
Proof
Since
, we obtain that
is not a
path. So, we have
Next, let Π
be a partition of
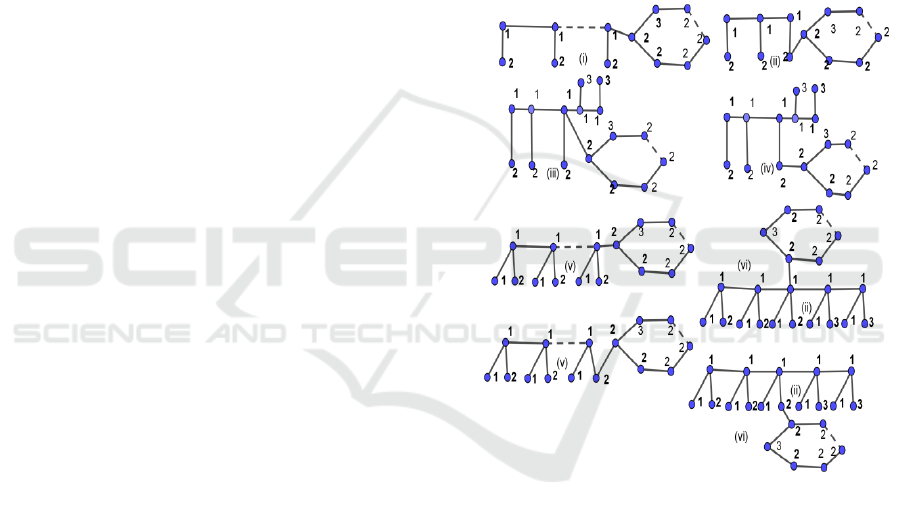
, look at Figure 1.
Figure 1: The resolving partition of B(G
1
,C
3
, uv) where
(i,ii,v,vi)
and (iii,iv,vii)
with
.
By definition of Π at Figure 1, it is easy to say that
is a resolving partition of
. So, we
have
.
Lemma 3.2. If
and
,
, and
, then
ICMIs 2018 - International Conference on Mathematics and Islam
218
Proof.
To easy our notation, let
.
Without loss of generality, let
. This proof
considers three cases.
Case 1. For , Since is not a path, then
. Let be a partition
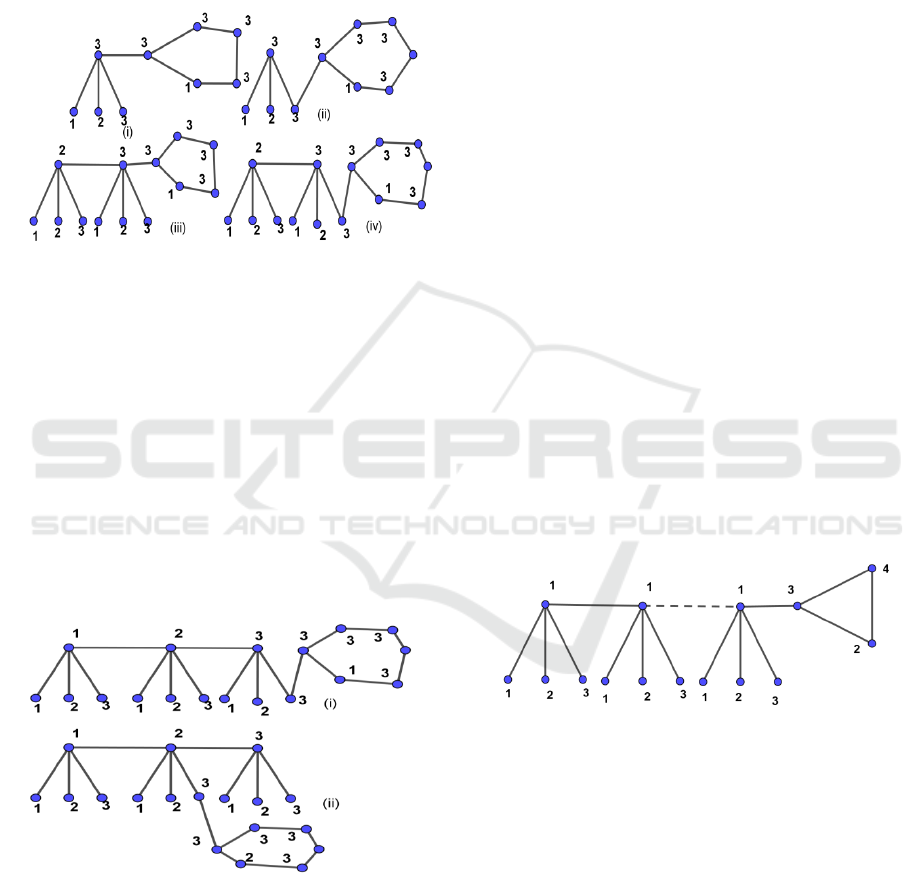
of , look at Figure 2.
Figure 2: The resolving partition of
where
(i,ii)
and (iii,iv)
.
By definition of Π at Figure 2, it is clear that Π is
a resolving partition of
. Let in
. If
then they are
distinguished by
or
. If
then
they are distinguished by some vertex which adjacent
to or
or
.
If
and
then they are distinguishe
.
So, we have
.
Case 2. For and is a leaf of
, since is
not a path, then . Let
be a partition of , look at Figure 3.
Figure 3: The resolving partition of
where is a leaf of .
Base on the definition of Π at Figure 2, it is clear
to say that Π is a resolving partition of
. So, we have
, where u is aleaf of
.
Case 3. We will show that . For a
contradiction that , let
be a resolving partition of . Since each
vertex
is adjacent to three leaves
, without loss
of generality
,
in a partition class
for
. Now we consider the vertices
for
. Since each
is a dominant vertex then the
vertices
contain at most in two partition
classes.
If
, then
. Since
,
,
, and
, then
will same to one of
representation of
,
,
and
. This implies
that
. If
, then
. Since
,
, then
will
same to one of representation of
, and
. This
implies that
. If
, then
. Since
,
, then
will
same to one of representation of
, and
. This
implies that
.
These implies
or
or
,
contradiction. As the consequences pd(H)≥ 4.
To show the upper bound of pd(H), we define a
new partition
of where
,
,
and
, look at Figure 4.
Figure 4: The resolving partition of
with
.
By definition of Π at Figure 3, it is easy to say that Π
is a resolving partition of
with
. So, we have
.
Theorem 3.1. If
are two cycles for ,
then
for
,
.
Proof.
Let
and
. Let u
1
v
1
be a bridge of B(C
m
,C
n
,u
1
The Partition Dimension of Bridge Graphs from Homogeneous Caterpillars and Cycle
219

v
1
). Define
is a partition of
where
,
and
. For
, if
then
are distinguished by
. The otherwise, they
are distinguished by
. For
, if
then are distinguished by
. The
otherwise, they are distinguished by
. The partition
class
is a singleton. These implies that is a
resolving partition of
. Thus, we obtain
.
Lemma 3.3 Let
be a homogeneous
caterpillar with, , and
be a
cycle with orde . If
is not a leaf and
, then
Proof:
Consider this proof in two cases.
Case 1. For , since there is a vertex
which is
adjacent to three leaves
then we obtain
. Let
of a recolving partition of
where
for
. Let
for some
.
Define a new partition ′
′
′
′
of
where ′
for
,
′
and ′
. We will show that ’
′
′
′
is a
resolving partitito of
.
Let in
. If are the leaves,
let
dan
then they are distinguished
by
. If (
for some ) and
, ,
then
is a dominant vertex but is not
a dominant vertex, so they are distinguished. If
and
, then they are distinguished by L
1
because
.
If
and
for
then they are
distinguished by
or
.
Case 2. For , since there are at least
verteces
which is adjacent to leaves
, then
we obtain
.
Let
for some
.
Define a partition
of
where
,
,
and,
for
. We
will show that
is a resolving partitito of
.
Let in
. If
then they are distinguished by
If
, then they are
distinguished by
.
Lemma 3.4 Let
be a homogeneous
caterpillar with , and
be a cycle with
orde . If
is a leaf and
,
then
Proof
We consider this proof in two cases.
Case 1. For , since there is a vertex
which is adjacent to leaves
, then we obtain
. Let
of a resolving partition of G
1
where
for
. Let
for some
.
Define a new partition
of
where
for
,
and
. We will show that
is a
resolving partition of
Let x,y in
. If are the leaves,
let
dan
then they are distinguished
by
.
If (
or
for some ) and
,
then
is a dominant vertex but is not a dominant
vertex. If
and
then they are
distinguished by
because
. If
and
for
then they are distinguished
by
or
.
These imply that the vertices are distinguished.
Case 2. For , since there are at least
vertices
which is adjacent to leaves
, then
we obtain
.
Let
for some
.
Define a partition
of
where
,
,
and,
for
. Let
in
. If
, then
they are distinguished by
. If
, then they are distinguished by
.
The following theorem gives the upper bound of
partition dimension of the bridge graph from any
connected graph and a cycle
.
ICMIs 2018 - International Conference on Mathematics and Islam
220

Theorem 3.2. Let
be a connected graph and
be a cycle with orde . If
and
, then
.
Proof.
Let
and be a bgidge of
with
. Suppose
is a resolving partition of and
and
be a
partition of
where
for
,
and
.
Let x be two distinct vertices of
.
We consider in three cases.
Case 1. the vertices in
.
If
, then they are distinguished by
′
. If
, then consider a
partition class
in
which is distinguishing x, y.
Since ′
and the vertices in
, then the vertices x, y are
distinguished by ′
.
Case 2. the vertices in
.If
, then they are
distinguished by ′
. , then
they are distinguished by ′
.
Case 3. the vertex in
and
in
. By definition a
partition Π, we only have in
. If
, then they are distinguished by
′
. If
, then we consider
′
. Since ′
, we have ′
. This implies that the
vertices are distinguished by ′
.
As the consequences that Π
′
′
′
′
is a resolving partition of
.
So, we have
≤ pd(G)+1.
4 CONCLUSIONS
In this paper, we obtained the partition dimension of
the bridge graphs,
from two
special graph namely the homogeneous caterpillar as
and a cyclic graph as
. The results show that the
partition dimension
where partition dimension of the
homogeneous caterpillar is .
ACKNOWLEDGEMENTS
This research was supported by Research Grand
”Program Hibah Riset Dasar Ristek DIKTI” 2018,
Ministry of Research, Technology and Higher
Education.
REFERENCES
Amrullah, Assiyatun, H., Baskoro, E. T., Uttunggadewa, S.,
and Simanjuntak, R., 2013. The Partition Dimension for
a Subdivision of Homogeneous Caterpillars. AKCE
International Journal of Graphs and Combinatorics
10.3, 317-325.
Amrullah, Darmaji and Baskoro, E. T., 2015. The partition
dimension for homogeneous firecrackers. Far East
Journal of Applied Mathematics, 90, 77 - 98.
Chartrand, G., Salehi, E., and Zhang, P., 2000. The partition
dimension of graph. Aequationes Mathematicae, 59,
45-54.
Chartrand, G., Salehi, E., and Zhang, P., 1998. On the
partition dimension of graph. Congressus
Numerantium, 130, 157-168.
Darmaji, Uttunggadewa, S., Simanjuntak R., and Baskoro,
E. T., 2009. The partition dimension of a complete
multipartite graph, a special caterpillar and a windmill.
J. Combin. Math. Combin. Comput. 71, 209-215.
Khuller, S., Raghavachari, B., and Rosenfeld, A., 1996.
Landmarks in graphs. Disc. Appl. Math. 70, 217–229.
Shanmukha, B., Sooryanarayana B. and Harinath, K. S.,
2002. Metric dimension of wheels. Far East J. Appl.
Math. 8 (3), 217–229.
Yero, Ismael G., and Juan A. Rodrguez-Velzquez, 2010. A
note on the partition dimension of Cartesian product
graphs. Applied Mathematics and Computation 217.7,
3571-3574.
Yero, Ismael G., Dorota K., and Juan A. Rodrguez-
Velzquez, 2011. On the metric dimension of corona
product graphs. Computers & Mathematics with
Applications, 61.9, 2793-2798.
The Partition Dimension of Bridge Graphs from Homogeneous Caterpillars and Cycle
221
