
Modified Firefly Algorithm using Smallest Position Value for
Job-Shop Schedulling Problems
Muhaza Liebenlito
1
, Nur Inayah
1
, Aisyah Nur Rahmah
1
and Ario Widiatmoko
2
1
Departement of Mathematics, UIN Syarif Hidayatullah Jakarta, Jl. Ir. H. Juanda No. 95, Tangerang Selatan, Indonesia
2
Department of Informatics, University of Sriwijaya, Jl. Srijaya Negara, Ilir Barat I, Kota Palembang, Indonesia
ario_widiatmoko@student.unsri.ac.id
Keywords: Job-Shop Scheduling Problem, Modified Firefly Algorithm, Smallest Position Value, Minimizing
Makespan.
Abstract: In this paper, we will modify the firefly algorithm to find the minimum makespan of job-shop scheduling
problem. Firefly algorithm generally is used to solve continuous optimization problem which is have to
modify by adding smallest position value to fit the discrete optimization problems, named Modified Firefly
Algorithm–Smallest Position Value (MFASPV). The result from MFASPV is compared with Bi-directional
algorithm, Tabu Search, and Discrete Firefly Algorithm. The MFASPV obtain minimum makespan as good
as Tabu Search and outperform the Discrete Firefly Algorithm and Bi-directional Algorithm.
1 INTRODUCTION
One of the scheduling problems often encountered
by the manufacturing industry is the job-shop
scheduling or Job-Shop Scheduling Problem (JSSP).
JSSP is sorting out the creation or work of the job as
a whole with the order of the machine through each
different job. JSSP is classified into the
combinatorial or discrete optimization problem. The
computation complexity for JSSP has been
categorized into Nondeterministic Polynomial-hard
problem (NP-hard) if the , where is the
number of machine(Garey et al., 1976).Because of
its complexity, many research has been developed to
solve this problem. In the paper (Dell’Amico &
Trubian, 1993) use Tabu Search (TS) and Bi-
directional (Bidir) algorithms to solve JSSP by
minimizing the makespan.
In the 2009, Xin-She Yang developed a bio-
inspired algorithm called Firefly Algorithm (FA) to
handle continuous optimization problem (Yang,
2009). In that paper shown FA outperform the
Genetic Algorithm (GA), Particle Swarm
Optimization (PSO) and Differential Evolution
(DE). Furthermore, the FA can be applied in various
continuous nonlinear optimization problem in any
Engineering problems (Yang & He, 2013).
In the 2009, Tasgetiren et al. solved the flow-
shop scheduling problem using PSO combined with
Smallest Position Value (SPV) rule. The SPV rule
used to convert continuous variables on PSO
mechanism into discrete variables (Tasgetiren et al.,
2009). Recently, the paper of K.C. Udaiyakumar and
M. Chandrasekaran proved that Discrete Firefly
Algorithm (DFA) which they proposed can be used
to solve JSSP by minimizing makespan
(Udaiyakumar & Chandrasekaran, 2014). However,
four of the twenty-five of Lawrence problems that
tested have not met the optimum value.
Based on the explanation above, we tried to
modify the FA with SPV rule to solve the JSSP. The
results will be compared with previous results TS
and Bidir (Dell’Amico & Trubian, 1993) and DFA
(Udaiyakumar & Chandrasekaran, 2014) which
solved the same problem that provided by Taillard
benchmark (Taillard, 1993).
2 PROBLEM DESCRIPTION
The JSSP can be defined as follows, given a
sequence
jobs and
machines. Job
consist of sequence of operations
which must be processed in this order, i.e. we have
precedence constraints of the form
,
Liebenlito, M., Inayah, N., Rahmah, A. and Widiatmoko, A.
Modified Firefly Algorithm using Smallest Position Value for Job-Shop Schedulling Problems.
DOI: 10.5220/0008516600230027
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 23-27
ISBN: 978-989-758-407-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
23
where (Brucker, 2007). The
operation
of job has to be performed in the
predefined order by specified machines
within
processing time. Each machine can process only one
job at the same time and each job can be processed
by only one machine at the same time. The problem
is to find a feasible schedule which minimizes the
makespan which is some objective function
depending on the finishing times
of the last
operations
of the jobs called. The makespan
denoted
(1)
where
is waiting time.
The problems can be represented as disjunctive
graph (Bażewicz et al., 2000; Kuhpfahl, 2016). Let
is disjunctive graph with
the operation -th of job denoted by node
and node 0 as starting node and node 1 as
ending node. Arc of node to node
is element of . For all job , there is one arc that
connects node 0 to and one arc connects node
to node 1, where node represents as the
last operation of job . Each arc connects from
node to node and has a weight
that represents as processing time of operation -th
of job . The weight of arc which connects from
node 0 to node is 0 and weight of arc from
node to node 1 is processing time of operation
of job . denotes a set of edges that connects
node of all different jobs which
processed on the same machines.
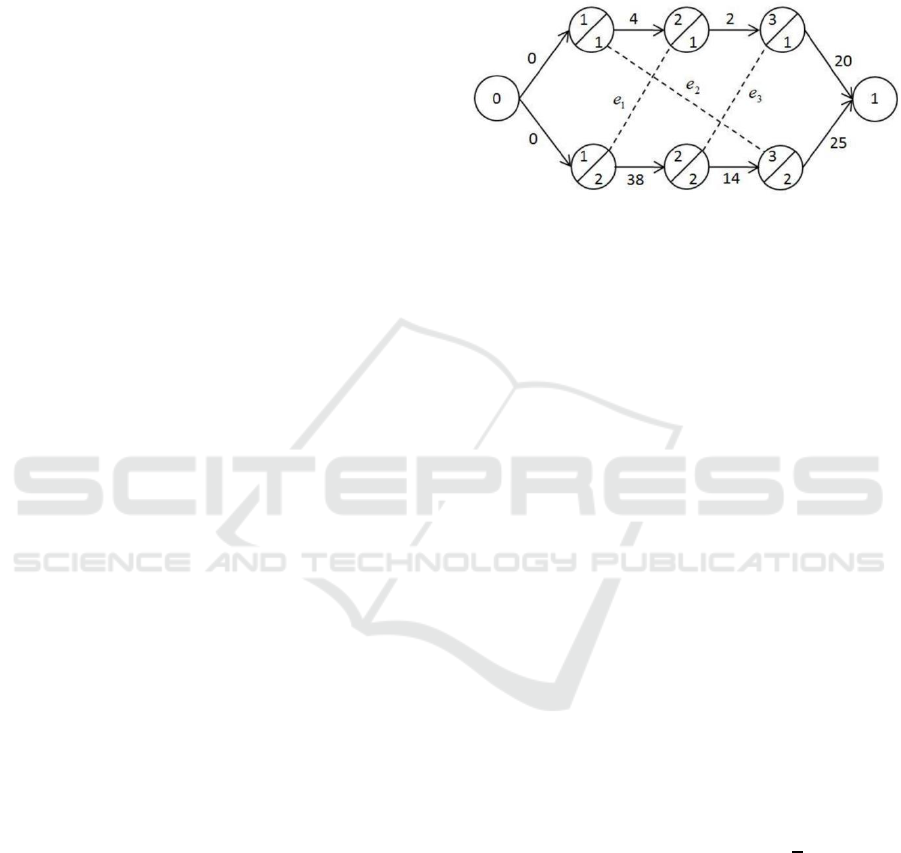
For more details see the following example,
given two jobs
with order of operations and
the jobs processed in three machines
within
processing time. The operations of each
jobs can be represent as matrix,
.
and its processing time,
.
In Figure 1, there are three edges
which is
the element of . Its edges have dash line which
represent as the possible solution of the problem.
The edge
connects the vertices and ,
it because
and
processed in the same
machine
as well as
and
. Then the total
weight of its longest path represent as makespan.
Figure 1: Representation of disjunctive graph for the
example problem.
3 FIREFLY ALGORITHM
Firefly Algorithm (FA) is meta-heuristic algorithm
inspired by flashing of the fireflies. FA first
introduced by Xin-She Yang to solve Multimodal
Optimization (Yang, 2009). There are three
important things on the FA, that is:
• Light intensity proportional to the objective
function
.
• The attractiveness function of fireflies denoted
(2)
where
represents the distance between any two
fireflies
and
; and the number of fireflies
denoted . The Parameters
and
.
• The movement of fireflies denoted
(3)
where is a vector represents controlling step-
size parameter and it has a value ;
is random variables whose uniformly
distribution ; the operator is vector-
scalar multiplication.
The pseudo-code FA formulate as Algorithm 1.
ICMIs 2018 - International Conference on Mathematics and Islam
24

Algorithm 1: Pseudo-code continuous FA.
Input:
Objective Function
; number of
population ; FA parameters:
and ;
and maximum iteration MAXITER.
Output:
Best
.
1.
Generate the initial population
,
2.
Evaluate
3.
while ( MAXITER) do
4.
for to do
5.
for to do
6.
if
then
7.
Calculate the attractiveness
with distance using (1).
8.
Move firefly to using
(2).
9.
end if
10.
Evaluate the objective function
11.
end for
12.
end for
13.
Rank the fireflies and find the current
best.
14.
end while
In Algorithm 1 starts with input FA parameters,
maximum iteration MAXITER, number of firefly
population , and define the objective function . If
we will find maximum of the objective function then
set
in step 6. Otherwise, if we find minimum
of objective function then set
.
4 OUR PROPOSED ALGORITHM
The JSSP belongs to the combinatorial optimization
problem where the decision variable is positive
integer. Therefore, the Algorithm 1 should be
adapted in order to solve the JSSP problem. To
change continuous decision variables into discrete
variables in Algorithm 1, we use SPV which firstly
introduced by (Tasgetiren et al., 2004). The pseudo-
code SPV has shown as follows:
Algorithm 2: Pseudo-code SPV.
Input:
.
Output:
.
1.
2.
′
′
3.
′
4.
′
′
′
On Algorithm 2, input is a set of random
numbers which have elements. The input is the
number of machine and is the number of job. In
Step 2 Algorithm 2, sort the elements of
ascendingly. Then in Step 3, contains the index of
elements of that has been sorted.
On problem example in section II we have
and , so based on Algorithm 2 in Step 2 we get
. Let we generated the values of
.
Based on Algorithm 2 in Step 2, obtain the sorted
elements of that stored in
.
In Step 3, is set that contains the indices of sorted
elements of , i.e.
On Algorithm 2 in Step 4, each of elements of
the modular operation and depend on the number of
job , we get
Set is feasible solution of the problem example in
section II which represents the order of operations
In Figure 2, node is predecessor from
, because the operation
is executed before
the operation
. The successor from
is, because
is executed after
finished.
Thus, longest path of its disjunctive graph is
whose total weight is
.
Figure2: Disjunctive graph for the feasible solution in
Problem Example in Section II.
Modified Firefly Algorithm using Smallest Position Value for Job-Shop Schedulling Problems
25

5 EXPERIMENTAL RESULTS
The result from our proposed algorithm called
MFASPV. Compared to the previous results from
Bidir and TS (Dell’Amico & Trubian, 1993), DFA
(Udaiyakumar & Chandrasekaran, 2014) on the
same benchmark Lawrence data provided by OR-
Library (Beasley, 1990). The summary of
benchmark data can be seen in Table 1. All
experiments were performed on Notebook Intel
Celeron N2840 @2.16 GHz with 4 GB RAM, and
the code was compiled using Microsoft Visual C++.
We use the number population and
maximum iteration MAXITER for all
benchmark data. The FA Parameters which used in
this experiment i.e. , ,
, and
. To measure the performance of each
algorithm, we use the formula
(4)
where
is the results from each algorithms
and
is the optimal value for Lawrence data
that provided by Taillard (Taillard, 1993).
Table 1: Summary of benchmark data.
Job
Machine
Problem Names
10
5
La05
15
5
La09, La10
20
5
La11, La14
The best makespan results obtained using
MFASPV, Bidir, TS, and DFA are shown in Table
2. From Table 2 can be seen the comparison of the
best makespan results from the Bidir, TS, DFA, and
MDFA-SPV algorithms. Referring to Opt, the TS
and MFASPV algorithms on JSSP is able to produce
the best makespan for all benchmark, while DFA is
able to produce the best makespan in four problems
and the Bidir algorithm is able to produce the best
makespan only in two problems.
Table 2: Summary of benchmark data.
Problem
Name
Opt
Bidir
TS
DFA
MFA
SPV
La05
593
593
593
593
593
La09
951
1017
951
951
951
La10
958
958
958
958
958
La11
1222
1259
1222
1222
1222
La14
1292
1294
1292
1295
1292
To evaluate the performance of the four
algorithms, we used (4). The percentage of
performance is presented in Table 3. From Table 3
seen that the average performance of the Bidir and
DFA algorithms is less than 100%, it means that the
makespan results obtained using both algorithms
have not been able to achieve Opt. While the
average performance for TS and MDFA-SPV
algorithms is 100%, which means the results of
makespan obtained using both algorithms are able to
achieve the Opt.
Table 3: Summary of benchmark data.
Problem
Name
Bidir
TS
DFA
MFASPV
La05
La09
La10
La11
La14
Mean
6 CONCLUSIONS
In this paper, our proposed algorithm which named
as MFASPV is tested using Taillard benchmark
problem available in the literature. MFASPV
compared with previous results Bidir, TS, and DFA
to find minimum value of makespan from the data
benchmark that provided by OR-Library. The
performance of MFASPV is found to be good and
able to achieve the best for five Lawrence problems.
REFERENCES
Bażewicz, J., Pesch, E. & Sterna, M., 2000. The
disjunctive graph machine representation of the job
shop scheduling problem. European Journal of
Operational Research, 127(2): 317–331.
Beasley, J. E., 1990. OR-Library: Distributing Test
Problems by Electronic Mail. The Journal of the
Operational Research Society, 41(11): 1069–1072.
Brucker, P., 2007. Scheduling algorithms. 5th ed. Berlin ;
New York: Springer.
Dell’Amico, M. & Trubian, M., 1993. Applying tabu
search to the job-shop scheduling problem. Annals of
Operations Research, 41(3): 231–252.
ICMIs 2018 - International Conference on Mathematics and Islam
26

Garey, M.R., Johnson, D.S. & Sethi, R., 1976. The
Complexity of Flowshop and Jobshop Scheduling.
Mathematics of Operations Research, 1(2): 117–129.
Kuhpfahl, J., 2016. Job Shop Scheduling with
Consideration of Due Dates: Potentials of Local
Search Based Solution Techniques. Gabler Verlag.
Taillard, E., 1993. Benchmarks for basic scheduling
problems. European Journal of Operational Research,
64(2): 278–285.
Tasgetiren, F., Chen, A., Gencyilmaz, G. & Gattoufi, S.,
2009. Smallest Position Value Approach. In
Differential Evolution: A Handbook for Global
Permutation-Based Combinatorial Optimization.
Studies in Computational Intelligence. Springer,
Berlin, Heidelberg: 121–138.
Tasgetiren, M. F., Sevkli, M., Liang, Y. & Gencyilmaz,
G., 2004. Particle swarm optimization algorithm for
single machine total weighted tardiness problem. In In
Proceedings of the 2004 Congress on Evolutionary
Computation (CEC’04. 1412–1419.
Udaiyakumar, K. C. & Chandrasekaran, M., 2014.
Application of Firefly Algorithm in Job Shop
Scheduling Problem for Minimization of Makespan.
Procedia Engineering, 97: 1798–1807.
Yang, X.-S., 2009. Firefly Algorithms for Multimodal
Optimization. In Stochastic Algorithms: Foundations
and Applications. Lecture Notes in Computer Science.
International Symposium on Stochastic Algorithms.
Springer, Berlin, Heidelberg: 169–178.
Yang, X.-S. & He, X., 2013. Firefly algorithm: recent
advances and applications. International Journal of
Swarm Intelligence, 1(1): 36–50.
Modified Firefly Algorithm using Smallest Position Value for Job-Shop Schedulling Problems
27
