Size Effect of Bending Properties of Zirconia Ceramics Based
on Cosserat Theory
Y Q Xu
1,*
, M M Li
2
and X Huo
1
1
Department of Civil Engineering, Beijing jiaotong University, Beijing 100044,
China.
2
Beijing NO.6 Construction Engineering Quality Test Department CO.,LTD. No.1
Xinhua Road, Fengtai District, Beijing 10076,China.
Abstract. In order to study the size effect of zirconia ceramics flexural properties , based on
the Cosserat generalized continuum theory, the zirconia ceramic flexural specimens with
different heights were numerically simulated, and the intrinsic size parameters of zirconia
ceramics were determined by comparing with expe rimental data. Compared with the classical
continuum theory, it is verified that the calculated value of bending strength based on
Cosserat theory is closer to the experimental results, which proves that Cosserat theory can
explain the size effect of zirconia ce ramics flexu ral strength. The equation of size effect of
nominal bending strength and nomina l bending stiffness is obtained by numerica l regression
based on the theoretical values of classical continuum.
1. Introduction
Zirconia ceramics have many advantages, such as high hardness, high strength, and corrosion
resistance and wear resistance. They are widely used in the field of micro forming. The experimental
results show that the flexural properties of zirconia ceramics increase with the decrease of specimen
height, showing obvious size effect [1].
The classical continuum mechanics considers an object to be composed of a continuous
distribution of particles without a geometric size. It is believed that the state of any point of matter
depends only on the point or the history of the point, without the influence of other material points.
Therefore, there are obvious limitations in describing the bending properties of zirconia ceramic
specimens with different heights, which can’t explain the bending property size effect caused by the
change of beam height. From a statistical point of view, it is reasonable to assume that an object is
made up of an ideal continuous medium when the macroscopic size of an object is much larger than
the characteristic size of the material microstructures. But when the macroscopic dimension of the
object is close to the characteristic size of the material microstructure, such assumption will cause a
larger deviation.
In fact, any material is made up of material points with geometric dimensions. In 1909, French
scientists Cosserat E. and F. two brothers, based on the classical continuum theory, put forward
generalized continuum mechanics [2], which considered objects to be composed of continuous rigid
particles of a certain size. Each particle can be both translational and rotatable. And the couple stress,
rotational gradient and intrinsic size of the material are introduced into the basic equations. Therefore,
Xu, Y., Li, M. and Huo, X.
Size Effect of Bending Properties of Zirconia Ceramics Based on Cosserat Theory.
In Proceedings of the International Workshop on Materials, Chemistry and Engineering (IWMCE 2018), pages 371-377
ISBN: 978-989-758-346-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
371

Cosserat theory can explain the scale effect phenomenon of materials at different scales in a
phenomenological way [3]. Many scholars have applied the Cosserat theory to explain the size effect
of metal and polycrystal [4-7] in micro scale, but the size effect of the mechanical properties of brittle
materials in the macro scale is very little. The study on the size effect of zirconia ceramic bending
performance based on Cosserat theory is still blank. In this paper, the size effect of the bending
properties of zirconia ceramics is studied by the comparison of the numerical simulation analysis and
model test based on the Cosserat theory.
2. Basic equations of plane Cosserat theory
The basic unknown quantities of the plane Cosserat theory are: two line displacements u, v and one
rotational displacement

; two normal stresses 

and 

, two shear stresses 

and 

, two
couple stresses 

and 

; two normal strains 

and 

, two shear strains 

and 

and two even
strains 

and 

.
2.1. Equilibrium differential equation
Compared with the classical elasticity theory, due to the consideration of couple stress, when the
physical forces are not considered, the equilibrium differential equations of plane problems are as
follows [2].
0 0 0
yx y xy y
xx
xy yx
x y y x x y
   


   

       
     
， ，
(1)
From the above equilibrium, it is known that due to the existence of couple stress, shear stress


and 

are no longer equal to each other.
2.2. Geometric equation
Considering the angle and curvature, the geometric equation is shown as follows:
x yx x
yy
xy
uu
x y x
v
v
yy
x

   



  
   
  






， ，
(2)
2.3. Physical equation
For ideal elastomers, the stress and deformation conform to Hooke's law.The relationship between
normal stress and normal strain is the same classical elasticity theory. Its relationship is shown as
follows on the plane stress condition:
11
( ) ( )
x x y y y x
EE
         ，
(3)
Because the shear stress is no longer equal to each other, the relationship between shear stress and
shear strain is different from that of classical elasticity theory. Based on the assumption of linear
elasticity and isotropy, the relationship between shear stress and shear strain can be expressed as
xy xy yx
ab    
，
yx xy yx
ba    
(4)
In the formula, a and b are the undetermined constants, and half of the sum of the formula (4) two
is
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
372

 
2 2 2
xy yx
xy yx
a b a b v u
xy




   
   



(5)
This is the normal symmetrical part of shear stress, which will cause shear deformation
xy
uv
yx




, which is consistent with classical elasticity theory and its coefficient
=
2
ab
G

.G is
the first shear modulus of the material. Half of the difference of type (4) two is
 
2 2 2
xy yx
xy yx
a b b a v u
xy




   
   



(6)
This is the antisymmetric part of the shear stress, which will cause the macroscopic angle
0
1
2
vu
xy







and its coefficient
c
=
2
ba
G

. G
c
is the second shear modulus of the material.
Therefore, for plane stress conditions, the relationship between shear stress and shear strain can be
expressed as
 
cc
cc
( ) ( )
()
xy xy yx
yx xy yx
G G G G
G G G G
  
  
   


   

(7)
For the relationship between the couple stress and the even strain, in order to maintain the unity of
dimension, the intrinsic size parameter of the material is introduced. The expression is given in the
paper [8].
22
44
x c x y c y
Gl Gl     ，
(8)
In the above equation,
2
4
c
Gl
is the bending stiffness of the material, in which
c
l
is the intrinsic
size of the material, which depends on the characteristic length of the material microstructures, such
as the modulus of elasticity and the Poisson's ratio, which are important parameters to measure the
properties of the material, and are not affected by the macro size, load and constraint conditions of
the structure. Although the intrinsic size is the dimension of the length, it is not equal to the particle
size of the material, so it can’t be obtained directly through the test. The determination of intrinsic
size parameters is the key to solve many mechanical problems by using Cosserat's basic equations
and boundary conditions. However, up to now, there has not been a search for the study of the
intrinsic parameter values of zirconia ceramics, there are no test standard and operation specification
can be referred to get through experiment.
3. Determination of intrinsic dimensional parameters of zirconia ceramics
The Cosserat theory of plane problem contains fifteen unknown functions and fifteen differential
equations, but its analytical solution is very difficult to obtain, and can only be solved by numerical
method. Therefore, this paper adopts Cosserat finite element mode [9] numerical simulation and
existing test data combination method to study the intrinsic parameters of zirconia ceramics.
3.1. Experimental data on size effect of bending strength of zirconia ceramics[1]
The samples were made of 6 kinds of sintered samples, the width of all was 4.7mm, and the height
was 92μm, 191μm, 289μm, 378μm, 474μm, 568μm respectively. The three point bending test was
carried out and the calculated span was 30mm.The formula for calculating the bending strength is
Size Effect of Bending Properties of Zirconia Ceramics Based on Cosserat Theory
373

2
3
2
f
Fl
bh
 
(9)
The
f

is nominal bending strength, F is the ultimate load, l is the calculation span, h is the
section height of the specimen, and b is the section width of the specimen. The bending strength of
specimens at different heights tested is shown in Table 1 [1].
Table 1. Material parameters of zirconia ceramics.
h/μm
F/N
f

/ MPa
92
0.88
998
191
3.39
890
289
6.80
780
378
9.40
630
474
12.67
540
568
18.20
540
It can be seen from Table 1 that the bending strength of zirconia ceramics decreases with the
increase of specimen height, showing obvious size effect.
3.2. Bending failure criterion of brittle materials
Because the tensile capacity of brittle materials is far less than its compressive capacity, when the
brittle material is bent, the damage occurs at the tensile fracture of the lower side fiber in the middle
cross section, and destroy all of a sudden with no significant deformation. Therefore, according to the
linear elastic failure characteristics of brittle materials, the maximum tensile stress failure criterion is
adopted to simulate the bending specimens of zirconia ceramics.
The maximum tensile stress criterion holds that, no matter what stress state of the material is in, as
long as the maximum tensile stress 

of the element is reached to the strength 

of the material,
the brittle fracture will be occurred. According to this criterion, the failure condition of material
fracture is


 

(10)
It can be seen from table 1, the bending strength of the specimen tends to be stable as the height of
the specimen increase. Therefore, the bending strength obtained from the specimen with the height of
568 μm is regarded as the flexural tensile ultimate strength of zirconia ceramics, which is
=540
b

MPa.
3.3. The determination of intrinsic dimensional parameters
Numerical analysis of zirconia bending specimens at different heights is carried out with different
intrinsic sizes. The calculated values are compared with the experimental values, as shown in Figure
1.
As shown in Figure 1, when the intrinsic size is 0, the calculated value is the theoretical solution
of the classical continuous medium. The deviation from the test results increases with the decrease of
the specimen’s height, and the deviation of the specimen is 84.8% when the specimen height is 92μm.
When the intrinsic size is between 20~40μm, the deviation between calculated value that based on
Cosserat theory and experimental value is relatively small. It can be seen that the intrinsic size of
zirconia ceramics should be in the range of 20~40μm. In addition to the specimens with height of
92μm, the deviation of the numerical solution and the test value are basically the smallest, when the
other height specimens are basically the same intrinsic size as 35μm. When the intrinsic size of the
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
374

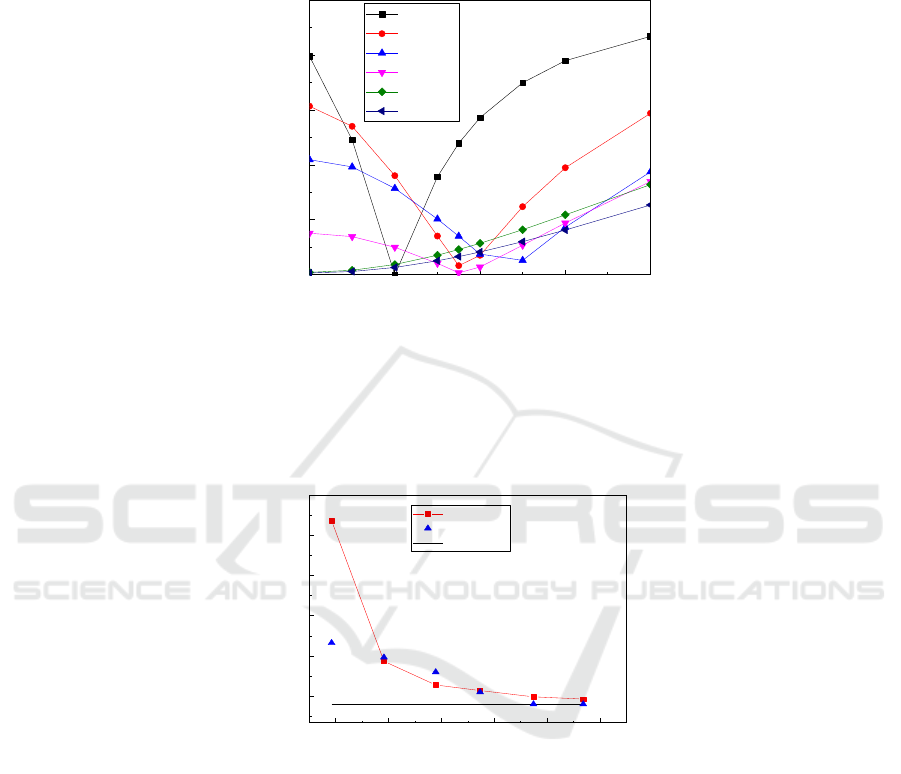
specimen with height of 92μm is 20μm, the deviation from the test value is the smallest, which may
be because the height is smaller, the pores in sintering are easier to discharge, the internal porosity
decreases, the sintering of the sample is more compact, and the internal defects of the material are
less, resulting in the decrease of the intrinsic size.
0 20 40 60 80
0
20
40
60
80
100
Deviation between numerical solution
and experimental value /%
intrinsic size /mm
h=92 m
h=191m
h=289m
h=378m
h=474m
h=568m
Figure 1. Deviation between numerical solution and experimental value with different intrinsic sizes.
The intrinsic dimension of zirconia ceramics is equal to 35μm, and the three point bending
loading test is simulated numerically. The experimental values, classical continuum mechanics
solutions and numerical solutions based on Cosserat theory are compared and analyzed, and the
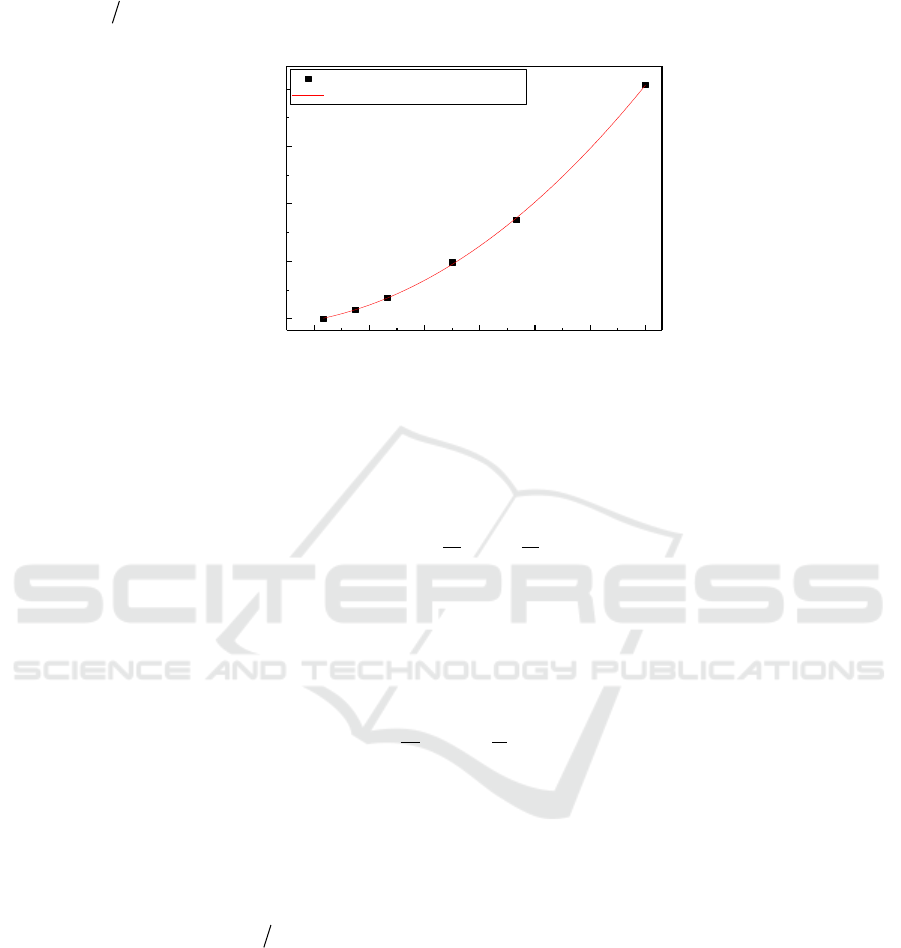
variation of nominal bending strength with the height of the specimen is shown in Figure 2.
100 200 300 400 500 600
600
900
1200
1500
1800
2100
Nominal bending strength /MPa
Specimen height /mm
Cosserat
Test
Classic
Figure 2. The variation of nominal bending strength with the height of the specimen.
It can be seen from Figure 2 that the bending strength of zirconia ceramics obtained by the
classical continuum theory is constant, which is independent of the size of the specimen, and can’t
explain the size effect of the bending strength of the specimens at different heights. The calculation
value of bending strength based on Cosserat theory and the test value are relatively closer, both are
increased with the decrease of the specimen’s height. When the specimen is high, the value of the
two is close to the theoretical value of the classical continuous medium, which shows that the size
effect of the bending strength is no longer obvious when the specimen is large enough.
4. The rule of size effect on the bending properties of zirconia ceramics
4.1. The rule of size effect of bending strength
In order to study the size effect of bending strength of zirconia ceramics, considering the influence of
the span and width is less, the span and width of the specimen are kept unchanged, and the three
Size Effect of Bending Properties of Zirconia Ceramics Based on Cosserat Theory
375

point bending loading test is simulated with the Cosserat finite element model. When the relative
dimension
c
lh
is different, the ratio of the nominal bending strength
Nb

to the classical theoretical
solution
b

is shown in Figure 3.
0.05 0.10 0.15 0.20 0.25 0.30 0.35
1.0
1.5
2.0
2.5
3.0
Cosserat
Polynomial regression curve
Ratio of bending strength

Nb
/
b
l
c
/h
Figure 3. The dimensionless size effect law of bending strength.
The regression equation for the nominal bending strength
Nb

of zirconia ceramicsis obtained by
regression analysis of the numerical data:
2
= 1 0.1 17
cc
Nb b
ll
hh









(11)
4.2. The rule of size effect of bending stiffness
For the three point bending beam, according to the classical continuum theory, the bending stiffness
of the beam is as follows:
3
=4
b
Fh
k Eb
l 




(12)
The formula (12) shows that when the elastic modulus of the material, the width of the specimen
and the high span ratio are certain, the bending stiffness of the beam calculated by the classical
continuum theory is constant.
In order to study the size effect law of the bending stiffness of zirconia ceramics, the Cosserat
finite element model is used to simulate the three point bending beam with a height span ratio of
0.01.When the relative size
c
lh
takes different values, the ratio of the nominal bending stiffness
Nb
k
of the specimen to the classical theoretical solution
b
k
is shown in Figure 4.
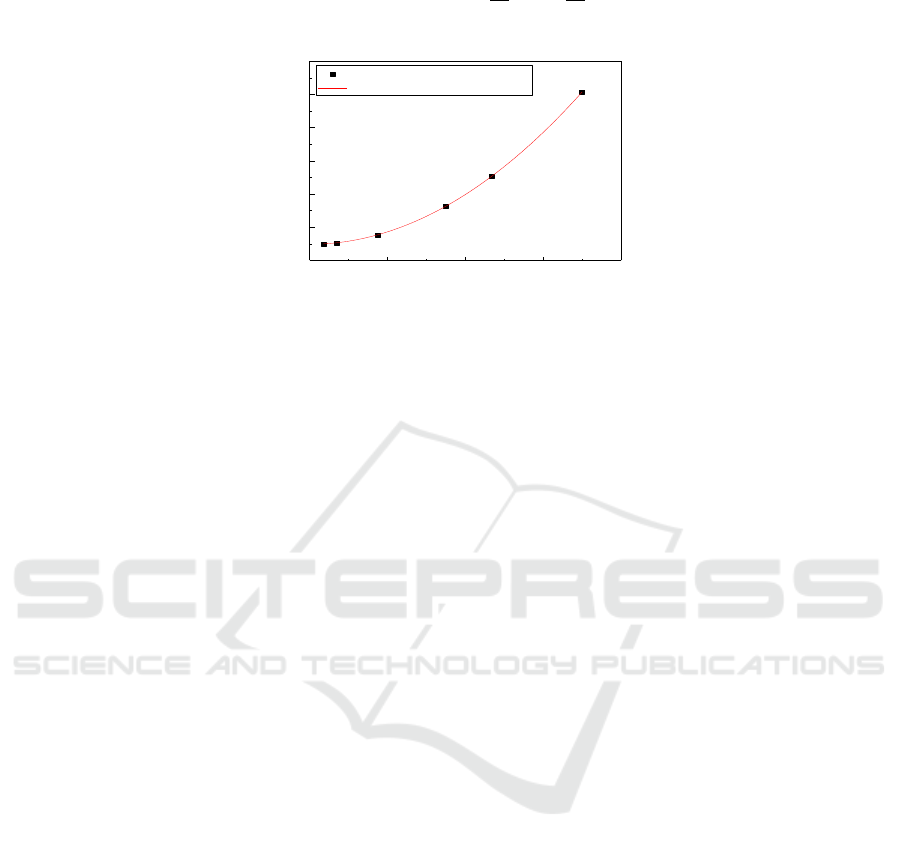
As shown in Figure 4, the nominal bending stiffness of zirconia ceramics increases with the
decrease of specimen height, and the bending stiffness exhibits obvious size effect. When the height
of the specimen is far greater than the intrinsic size of the material, the nominal bending stiffness
calculated by Cosserat theory is closer to the classical continuum theory, and the size effect is no
longer significant. By regression to the numerical simulation data, the equation of the nominal
bending stiffness
Nb
k
of zirconia ceramic with size is obtained as follows:
IWMCE 2018 - International Workshop on Materials, Chemistry and Engineering
376

2
1 0.02 18( )
cc
Nb b
ll
kk
hh

  


(13)
0.0 0.2 0.4 0.6 0.8
0
2
4
6
8
10
12
Cosserat
Polynomial regression curve
Nominal bending strength
k
Nb
/k
b
l
c
/h
Figure 4. The dimensionless effect law of bending stiffness.
5. Conclusions
On the basis of Cosserat theory, the range of intrinsic size parameters of zirconia ceramics is
determined by combining numerical simulation with flexural performance test data. The size effect
law of the bending properties of zirconia ceramics is proposed. The conclusion is as follows:
1) The intrinsic size of zirconia ceramics is deter-mined to be 20~40μm by comparison of theory
and experiment;
2) Considering the intrinsic dimensional parameters of the material, the bending strength of
zirconia ceramic based on Cosserat theory is in good agreement with the experimental results, and it
can explain the size effect of bending strength at different height beams;
3) The nominal bending strength and bending rigidity of zirconia ceramics increase with the
decrease of beam height.
4) The nominal bending strength of zirconia ceramics and dimensionless size effect equation of
nominal bending rigidity are obtained by numerical simulation regression analysis.
References
[1] Yang L, Tian S Y, Xia F and et al 2017 Size Effect of Flexural Strength of Zirconia Ceramics
Bulletin of the Chinese Ceramic Society vol 36(9) 3125-2127
[2] Cosserat E and Cosserat F 1909 Théorie des corps déformables Hermannet and Fils Paris
[3] Dai T M 1981 Brief Comments on the Development of the Cosserat Continuum Theory
Chinese Journal of Solid Mechanics vol 1 129-132
[4] Asmahana Z, Samsuel F, Anne F G and et al 2005 Cosserat continuum modelling of grain size
effects in metal polycrystals PAMM. Proc. Appl. Math. Mech vol 5 79-82
[5] Tang H X and Hu Z L 2013 Three Dimensional Cosserat Continuum Model and Finite
Element Analysis for the Size Effect of Micro-structure Chinese Journal of Computational
Mechanics vol 30(3) 399-405
[6] Amir M A, Seyed M S, Ghader R and et al 2015 Modelling the Size Effects on the Mechanical
Properties of Micro/Nano Structures Sensors vol.15 28543-28562
[7] Zhao B, Zheng Y R and Chen C Finite element method implementation of Cosserat theory and
scale effect simulation of micro-beam. 2010 Journal of Changsha University of Science and
Technology (Natural Science), vol 7(4), 37-42
[8] Mindlin R D 1962 Influence of couple-stress on stress concentrations Experimental Mechanics
vol 3(1) 1-7
[9] Li M M 2017 Establishment of Finite Element Model and Study on Size Effect of Concrete
Flexural Strength Based on Plane Cosserat Theory Beijing jiaotong University
Size Effect of Bending Properties of Zirconia Ceramics Based on Cosserat Theory
377