
A Stochastic Approach for Damage Modelling of Cast Alloys
Christian Mühlstätter
LKR Leichtmetallkompetenzzentrum Ranshofen GmbH,
Austrian Institute of Technology, Austria
Keywords: Damage Modelling, Triaxiality, Goodness-of-fit Test.
Abstract: The increasing interest of cast Aluminium alloys in structural application asks for appropriate simulation
approaches. Besides the constitutive behaviour, damage properties play an important role for this material.
The damage behaviour is significantly influenced by the microstructure. Due to the specific morphology of
cast microstructure and the random spatial deviation of voids, a novel concept of material modelling is
necessary. In this study, a concept for stochastic material characterisation and modelling in structural Finite
Element simulations is introduced. Therefore, a test matrix for experimental tests is discussed. Based on the
generated experimental data a stochastic evaluation is performed by a goodness-of-fit test. The achieved
characterisation knowledge is used to introduce the concept for stochastic material modelling of Aluminium
cast alloys.
1 INTRODUCTION
Since light weight demand raises in automotive
application, cast Aluminium alloys gain more
relevance for structural parts. Therefore, an accurate
capturing of material behaviour is necessary for
structural Finite Elemente (FE) simulations. Due to
the casting process the material gets its characteristic
morphology with certain small amounts of voids
which is substantially influenced by process
parameters, e.g. time dependent pressure distribution,
cooling rate, flow behaviour. Furthermore, the quality
of melted Aluminium is a sensitive parameter which
depends on air exhibition duration and accuracy of
designated mass fraction for each alloy component.
The set of these parameters causes a material with
varying microstructure which results in
inhomogeneous mechanical properties. In
conventional modelling approaches, e.g. (Gurson,
1978) or subsequent works (Tvergaard and
Needleman, 1984) the material is considered as
continuum with smoothed micromechanical
behaviour. These models capture the damage
behaviour by the evolution of void fractions within
the material due to ductile fracture mechanisms.
Furthermore, phenomenological approaches are
proposed by (Wilkins, et al., 1980) and (Johnson and
Cook, 1985) which describe the material damage by
a triaxiality dependent fracture strain. The standard
implementation of these models is as well smoothed
and does not consider the spatial variation of material
parameters.
In this paper, a phenomenological approach
combined with a concept of stochastic consideration
for cast material characterisation and modelling is
introduced.
2 DUCTILE FRACTURE
Structural materials are characterised by several
engineering parameters, e.g. yield stress and tensile
strength. Furthermore, the damage behaviour is a
characteristic of a material which is composed by
the evolution of certain micromechanical
phenomena. Essentially, two different failure modes
can be observed at metallic materials which appear
as brittle or ductile fracture. The characterisation of
the failure mode is basically done by monitoring the
plastic strain until fracture occurs. Aluminium die
cast alloys show a ductile fracture behaviour with
distinct plastic deformations (Fagerholt, et al., 2010;
Muehlstaetter and Hartmann, 2016). The evolution
of ductile fracture is based on micromechanical
mechanisms including nucleation, growth and
coalescence of micro voids within a material as
depicted in Figure 1.
Mühlstätter, C.
A Stochastic Approach for Damage Modelling of Cast Alloys.
DOI: 10.5220/0006909904670471
In Proceedings of 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2018), pages 467-471
ISBN: 978-989-758-323-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
467
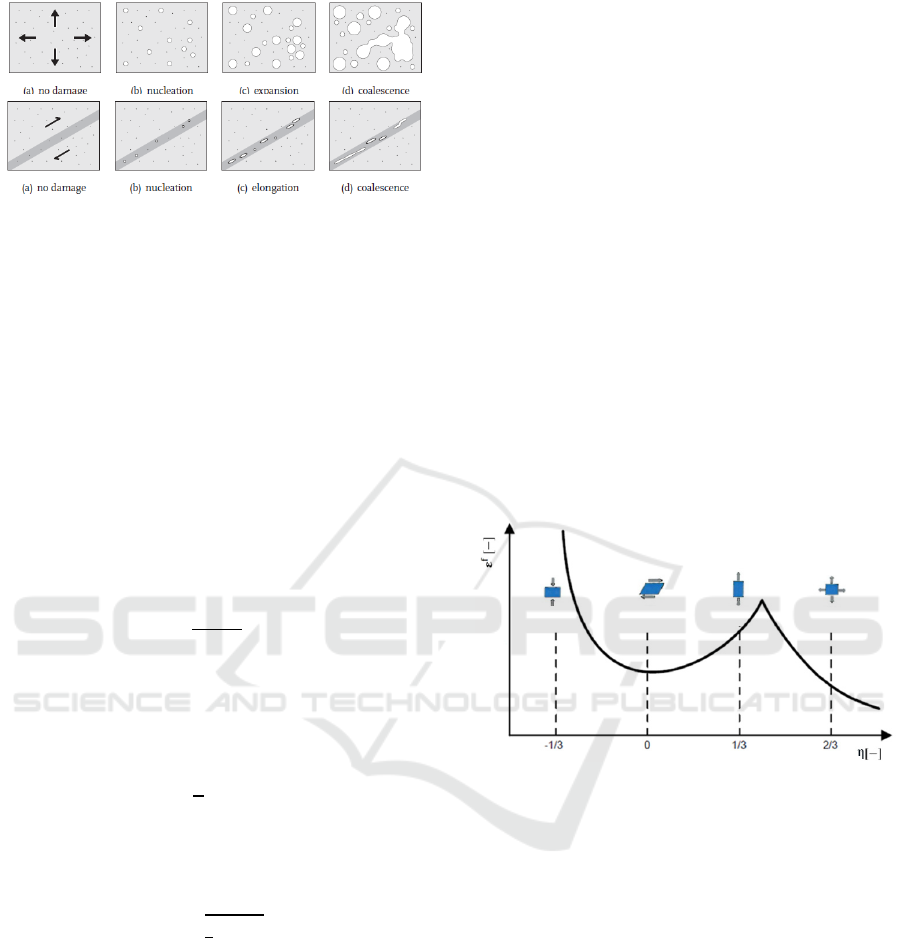
Figure 1: Evolution of material damage by different stress
states (Engelen, 2005).
2.1 Solid Mechanics
A certain stress state, denoted by the stress tensor,
causes a characteristic damage mechanism after
exceeding yield strength. Normal stresses (Figure 1
top) lead to expansion and coalescence of voids.
Shear stresses (Figure 1, bottom) cause the formation
of shear bands. Therefore, an arbitrary stress state
needs to be evaluated regarding the damage effect of
the material. A well-established method is proposed
by (Bao and Wierzbicki, 2004) which consider the
fraction strain as function of the stress triaxiality,
defined as
η=
.
(1)
The triaxiality quantifies a stress state in terms of the
multiaxiality by the ratio between the hydrostatic
stress σ
, given by
σ
=
1
3
(
)
,
(2)
which is extracted from the stress tensor and the
von Mises equivalent stress σ
, calculated as
σ
=
,
(3)
composed by the stress deviator
in Einstein
notation which is formulated as residual of the stress
tensor with respect to the hydrostatic strain, therefore
=−
(4)
with the threedimensional unity matrix .
2.2 Characterisation of Damage
Behaviour
For structural mechanics, numerical simulation
software calculates displacements which appears due
to external loads and boundaries. Therefore, strains
are determined based on a defined constitutive law
which leads to a stress field. In addition, the induced
stresses cause certain micromechanical effects and
the evolution of damage. As already outlined in the
previous section, the damage mechanism depends on
the stress state. State of the art damage modelling is
based on the approach of (Bao and Wierzbicki, 2004),
where a characteristic fracture strain is defined as
function of the stress triaxiality η (see Figure 2).
Based on this approach a damage variable D is
formulated as function of the plastic strain
and the
fracture strain function
(
η
)
:
D=
f
ε
,
(
η
)
(5)
Figure 2: Characteristic metal fracture strain curve as
function of the stress triaxiality (Bao and Wierzbicki,
2004).
Hence, for structural simulations including damage,
additional material characterisation effort is
necessary. Figure 3 shows a set of test coupons to
capture different stress states which cause various
damage mechanisms. Therefore, test geometries are
manufactured and tested under tension load. The
specific morphology within the gauge length, where
fracture occurs, leads to triaxiality regimes of 0, for
shear tensile and Merklein shear, to 0.33 for flat
tensile tests and 0.57 for notched test. The negative
triaxiality regime cannot be covered with this
characterisation strategy.
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
468
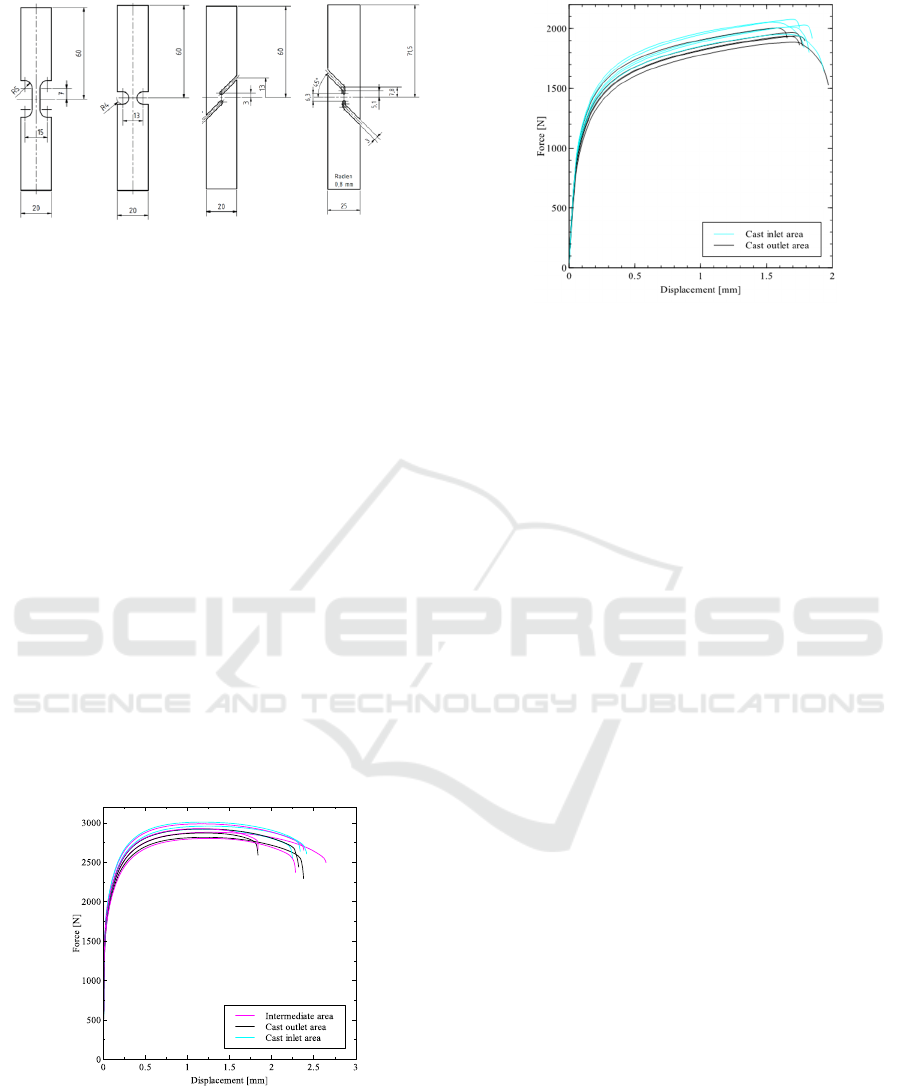
Figure 3: Test geometries for characterisation of the
damage behaviour (from left: flat tensile, notched, shear
tensile and Merklein shear).
2.3 Experimental Results
The intention of this study is to characterise a cast
material which is produced by a stable and steady
state die casting process. Therefore, the process runs
a certain time to ensure constant process parameters,
e.g. temperature field within the casting plant. The
test specimens are extracted from casted hat profiles.
For the experimental characterisation, a test matrix
with at least 10 valid tests of each test geometry is
defined. Furthermore, the spatial location of
extraction with respect to the casting inlet is
documented.
The output of these tests are force vs.
displacement curves. Figure 4 shows the results of the
flat tensile tests. The force-displacement curves show
a significant deviation for a pure tension load with
theoretical triaxiality of 0.33. A similar behaviour is
observed for the notched tension tests (Muehlstaetter,
2015).
Figure 4: Experimental force vs. displacement curves of flat
tensile tests for different regions within the casted part.
The test results of the Merklein tests are depicted in
Figure
5
. Deviation is also apparent in these results,
although it is lower than in the triaxiality regimes of
η0.33.
Figure 5: Experimental force vs. displacement curves of
Merklein test geometry for different regions within the
casted part.
3 STOCHASTIC EVALUATION
Based on the experimental data of the previous
chapter an evaluation regarding the stochastic
behaviour is performed.
3.1 Goodness-of-fit Test
In this section, a strategy for a stochastic
consideration of the experimental data is introduced.
The objective is to characterise the obtained
scattering of the force-displacement curves. The
scattering consists of the variation in the flow
behaviour and the failure displacement. This study
aims to consider only the failure displacement.
Hence, discrete failure displacement values are
extracted from the experiments.
By application of stochastic theory, the problem
appears as issue of seeking a formulation of a
potential underlying stochastic distribution.
Therefore, goodness-of-fit tests are available
(Schiefermayr and Weiß, 2014). These tests need an
initial estimation of a stochastic distribution including
their parameters, e.g. standard deviation for the
normal distribution, as input. Based on the
Cumulative Density Function (CDF) of this
stochastic distribution, the null hypothesis ʜ
is tested
against the alternative hypothesisʜ
.
ʜ
is defined as: The claim that the test data
follows the estimated stochastic distribution is true;
ʜ
has the opposite meaning. Several goodness-of-fit
tests are available in literature, e.g. (Schiefermayr and
Weiß, 2014). The application of each test depends on
the range of available data. In this study, the test data
is relatively low for a stochastic consideration.
A Stochastic Approach for Damage Modelling of Cast Alloys
469
Therefore, the Kolmogorov-Smirnov (KS) test which
delivers accurate results for low data is suitable.
This goodness-of-fit test is based on the steady
distribution proposed by Kolmogorov with the CDF
defined as
=1+2
(
−1
)
(
≥0
)
.
(6)
The random variable is the fracture strain
from the
experiments.
For the application of goodness-of-fit tests a
significance level α needs to be defined. The
significance level sets the probability, that the true
null hypothesis is rejected accidentally. A common
value for α is 5 %. Based on this parameter the
condition for the rejection of the null hypothesis is
formulated as
≥
(1−)/
√
(7)
whereas
is the Quantile of the Kolmogorov CDF
and is the amount of available test data for
. The
parameter is based on the experimental data and the
CDF of the estimated underlying distribution, defined
as
:=
(
)
−
(
)
. (8)
This parameter determines the maximum deviation,
or mathematically formulated as supremum between
the empirical CDF
(
)
, given by
(
)
=
,
(9)
and the estimated CDF.
in Equation 9 is the
number of data which fulfil the condition ≤
and
is the total number of test data. The second term in
Equation 8 is the CDF of the estimated stochastic
distribution. In applied sciences, many processes
succeed the normal distribution. Therefore, it is
reasonable to choose this distribution for the first
iteration of the KS test. The CDF of the normal
distribution is defined as
=
1
√
2π
exp−
(
−
)
2
.
(10)
The normal distribution has 2 parameters, the
expectation value and the variance which needs
to be defined by application of moment estimators.
Hence, and are calculated by the arithmetic mean
value and the standard deviation.
The introduced test of this chapter is applied on
the experimental data of the flat tensile test, depicted
in Figure 4. The determination of the condition for the
rejection of the null hypothesis from Equation 7
yields a value for T of 0.41. The determination of the
parameter T leads to a value of 0.139. Thus, the
condition of Equation 7 is not fulfilled, and the null
hypothesis is true. Furthermore, the tested data
follows the normal distribution.
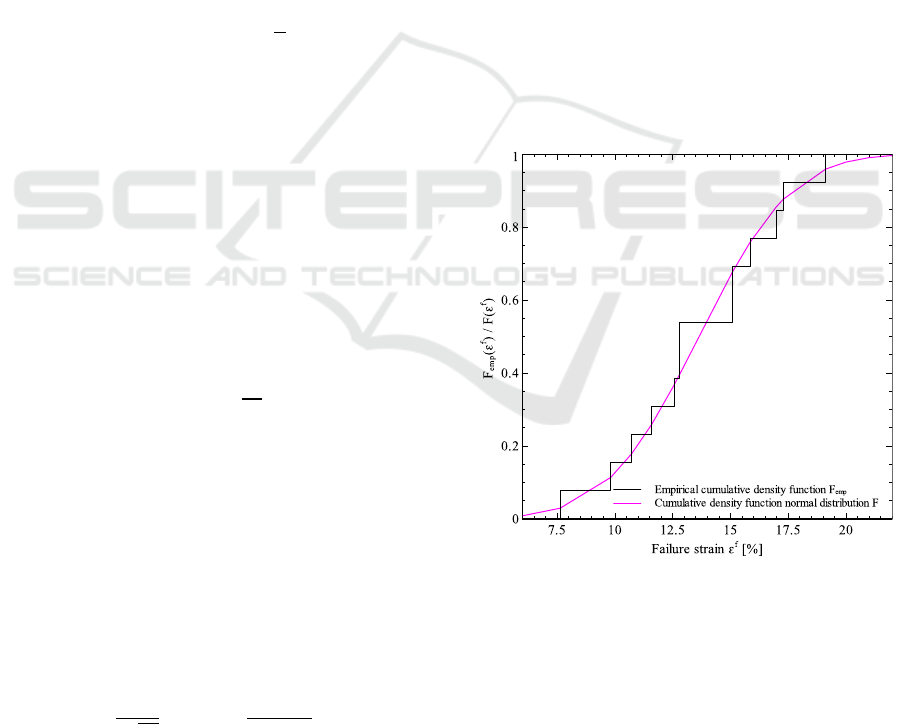
If the first iteration leads to a rejection of the null
hypothesis, an alternative distribution needs to be
defined for the second KS test iteration. The concept
of the KS test is depicted in Figure 6 in graphical
representation. The empirical density function
appears as step function in black line and the CDF of
the normal distribution with estimated parameters in
magenta line. The CDF of the normal distribution
crosses every plateau of the empirical CDF, except
at
=17.5. This is the visual interpretation of
Equation 8 with the supremum between
(
)
and
(
)
.
Figure 6: Visual representation of the Kolmogorov-
Smirnov goodness-of-fit test with normal distribution and
empirical CDF for tensile test data.
The application of this strategy for each test data
set builds the concept for the development of an
innovative approach for damage modelling. The
fundament of this approach is the consideration of
material damage proposed by (Bao and Wierzbicki,
2004) which is implemented in several Finite Element
codes, e.g. LS-Dyna. In addition, the stochastic
SIMULTECH 2018 - 8th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
470
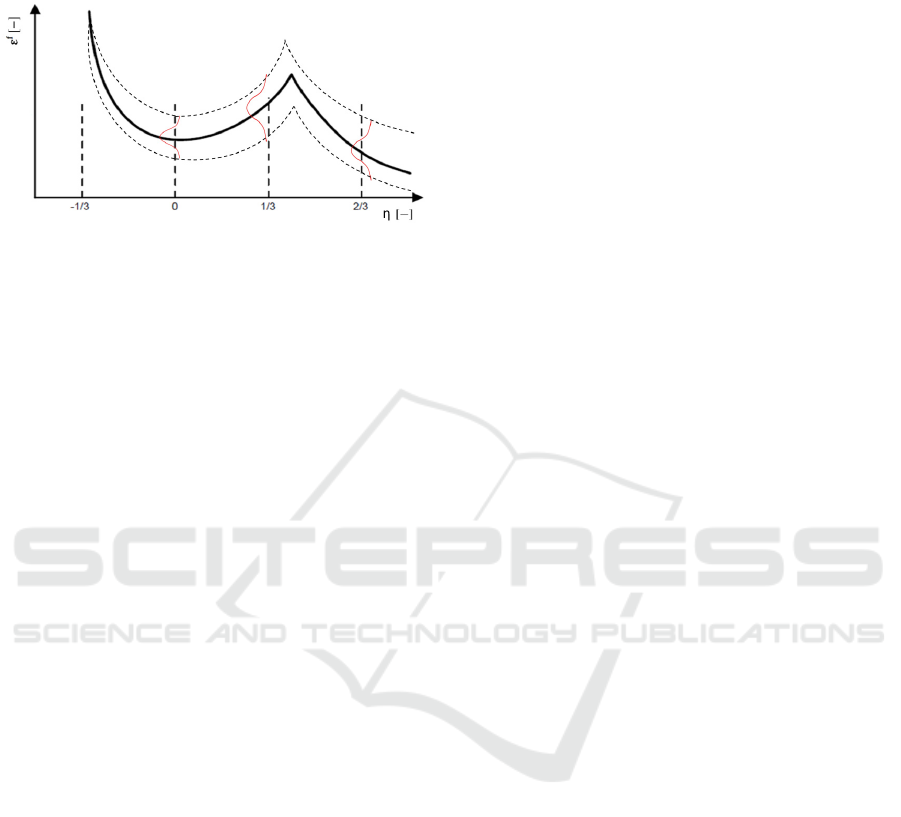
behaviour of a material is added by the concept of this
study. Figure 7 depicts this combined approach.
Figure 7: Schematic concept for the stochastic damage
modelling (red and dashed line) based on the approach of
(Bao and Wierzbicki, 2004) (black, solid line).
The black solid line represents the well-
established approach of (Bao and Wierzbicki, 2004).
The red Gauss’ curve at =0.33 is introduced by the
concept in this chapter. The remaining Gauss’ curves
are schematic for any probability function which
needs to be establish by the KS test. Based on the
probability functions, the dashed bounds are defined.
This concept is intended as input for a random
variable generator which delivers fraction strain
curves as function of the triaxiality for each
integration point in a simulation model. Hence, a
random field of material property is generated
initially for structural Finite Element simulations.
4 CONCLUSIONS
Damage modelling under consideration of the
fracture strain as function of triaxiality is a well-
established method. However, for cast Aluminium
alloys the inhomogeneous material/damage
behaviour is neglected. The introduced concept can
overcome this drawback and builds a potential for
more accurate capturing of material scatter of cast
Aluminium alloys.
ACKNOWLEDGEMENTS
This work has been supported by the European
Regional Development Fund (EFRE) in the
framework of the EU-program "IWB Investition in
Wachstum und Beschäftigung Österreich 2014-
2020", and the federal state Upper Austria.
REFERENCES
Bao, Y., Wierzbicki, T., 2004. On fracture locus in the
equivalent strain and stress triaxiality space.
s.l.:International Journal of Mechanical Sciences.
Engelen, R., 2005. Plasitcity induced Damage in Metals:
nonlocal modelling at finite strains. s.l.:Habilitation
thesis.
Fagerholt, E.; et al., 2010. Experimental and numerical
investigation of fracture in a cast aluminium alloy.
s.l.:International Journal of Solids and Structures.
Gurson, A. L., 1978. Porous rigid-plastic materials
containing rigid inclusions-yield function, plastic
potential and void nucleation. s.l.:The Physical
Metallurgy of Fracture.
Johnson, G. R., Cook, W. H., 1985. Fracture
characteristics of three metals subjected to various
strains, strain rates, terperatures and pressures.
s.l.:Engineering Fracture Mechanics.
Muehlstaetter, C., 2015. Versagensmodellierung von Al-
Gusswerkstoffen. s.l.: Master Thesis, Upper Austrian
University of applied sciences.
Muehlstaetter, C., Hartmann, M., 2016. Material modelling
of cast Aluminium by application of the Wilkins
Damage Model. s.l.:ECCOMAS Congress Proceedia.
Schiefermayr, K., Weiß, P., 2014. Wahrscheinlichkeits-
rechnung und Statistik. s.l.:Course book, Upper
Austrian University of applied sciences.
Tvergaard, V., Needleman, A., 1984. An analysis of ductile
rupture in notched bars. s.l.:Journal of the Mechanics
and Physics of Solids.
Wilkins, M. L., Streit, R. D., Reaugh, J. E., 1980.
Cumulative-strain-damage model of ductile fracture:
Simulation and prediction of engineering fracture tests.
s.l.:s.n.
A Stochastic Approach for Damage Modelling of Cast Alloys
471
