A Novel Method for Grouping Variables in Cooperative Coevolution

for Large-scale Global Optimization Problems

Alexey Vakhnin and Evgenii Sopov

Department of System Analysis and Operations Research, Reshetnev Siberian State University of Science and Technology,

Krasnoyarsk, Russia

Keywords: Large-scale Global Optimization, Variable Grouping Method, Cooperative Coevolution, Evolutionary

Algorithms.

Abstract: Large-scale global optimization (LSGO) is known as one of the most challenging problem for evolutionary

algorithms (EA). In this study, we have proposed a novel method of grouping variables for the cooperative

coevolution (CC) framework (random adaptive grouping (RAG))). We have implemented the proposed

approach in a new evolutionary algorithm (DECC-RAG), which uses the Self-adaptive Differential Evolution

(DE) with Neighborhood Search (SaNSDE) as the core search technique. The RAG method is based on the

following idea: after some predefined number of fitness evaluations in cooperative coevolution, a half of

subcomponents with the worst fitness values randomly mixes indices of variables, and the corresponding

evolutionary algorithms reset adaptation of parameters. We have evaluated the performance of the DECC-

RAG algorithm with the large-scale global optimization (LSGO) benchmark problems proposed within the

IEEE CEC 2010. The results of numerical experiments are presented and discussed. The results have shown

that the proposed algorithm outperforms some popular LSGO approaches.

1 INTRODUCTION

Many real-world problems deal with high

dimensionality and are driven by big data.

Optimization problems with many hundreds or

thousands of objective variables are called large-scale

global optimization problems. LSGO is still a

challenging problem for mathematical and

evolutionary optimization techniques. There exist

many examples of real-world LSGO problems from

different areas (Mei et al, 2014), (Jiang and Wang,

2014), (Lin et al, 2014) (data mining, engineering,

bioinformatics, optics, etc.).

The majority of hard real-world LSGO problems

is classified as the Black-Box (BB) optimization

problems. The key feature of the BB problems is that

there is no useful information about objective features

for improving the search process. We can only

request a fitness value

()

x for any point

from

the search space. Nevertheless, evolutionary

algorithms have proved their efficiency at solving

many BB optimization problems (Bäck, 1996),

(Gagn, 2012).

The general BB optimization problem can be

stated in the following way:



(



)



(



,



,…,



) → min/max



∈



(1)







≤



≤





, = 1,



(2)





(





,



,…,



)

≤0,



=1,



(3)

ℎ



(





,



,…,



)

=0,=1,



(4)

where ̅ ∈, ⊆



denotes the continuous

decision space, ̅ =(



,



,…,



)∈



is a vector

of decision variables, :  → 



stands for a real-

valued continuous nonlinear objective function.

Equation (2) defines side constrains, were 





and 





the lower and the upper bounds of a search interval,

respectively. Equations (3) and (4) define general

linear and nonlinear inequality and equality

constraints.

In this paper, we consider the unconstrained

minimization LSGO problem.

In this study, we have proposed a novel method

of grouping variables for the cooperative coevolution

framework, which is called random adaptive

Vakhnin, A. and Sopov, E.

A Novel Method for Grouping Variables in Cooperative Coevolution for Large-scale Global Optimization Problems.

DOI: 10.5220/0006903102610268

In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2018) - Volume 1, pages 261-268

ISBN: 978-989-758-321-6

261

grouping (RAG). We have implemented the proposed

approach in a new evolutionary algorithm (DECC-

RAG). We have evaluated the performance of the

DECC-RAG algorithm with the LSGO benchmark

problems proposed within the IEEE CEC 2010. The

performance of the DECC-RAG has been compared

with the classical differential evolution (DE), the

original Self-adaptive Differential Evolution with

Neighborhood Search (SaNSDE).

The rest of the paper is organized as follows.

Section 2 describes related work. Section 3 describes

the proposed approach. In Section 4 the results of

numerical experiments are discussed. In the

Conclusion the results and further research are

discussed.

2 RELATED WORK

2.1 Classical Differential and

Self-Adaptive Differential

Evolution with Neighborhood

Search (SaNSDE)

Differential evolution (DE) is one the most popular

and efficient evolutionary algorithm. DE is a

stochastic, population-based search strategy

developed by (Storn and Price, 1995).

One of the further development of DE is the

SaNSDE algorithm proposed by (Yang et al, 2008b).

We have chosen this algorithm for our investigation

because of self-adaptive tuning of its parameters

during optimization process.

As known, the performance of any evolutionary

algorithm strongly depends on its control parameters.

The general list of DE parameters contains the type of

mutation, the differential weight value and F the

crossover probability value CR. The main feature of

the SaNSDE algorithm is that the algorithm

stochastically select a type of mutation and values of

CR and F, and then adapts F and CR values based on

the success of implementing a mutation operation.

After a predefined number of generations, the

SaNSDE recalculates probabilities for selection of a

type of mutation and values of CR and F.

There exist many approaches for solving LSGO

problems using DE and other evolutionary

algorithms. We can divide all approaches into two

main categories: cooperative coevolution (CC)

algorithms with problem decomposition strategy and

non-decomposition based methods. As it has been

shown in many studies, CC approaches usually

demonstrates higher performance. The most popular

CC approaches use different strategies for grouping

of objective variables. Some well-known techniques

are the static grouping (Potter and Jong, 2000), the

random dynamic grouping (Yang et al, 2008c) and the

learning dynamic grouping (Omidvar et al, 2014)).

2.2 Cooperative Coevolution

Decomposition methods based on cooperative co-

evolution are the most popular and widely used

approaches for solving LSGO problems. Cooperative

coevolution (CC) is an evolutionary framework that

divides a solution vector of an optimization problem

into several subcomponents and optimizes them

independently in order to solve the optimization

problem.

The first attempt to divide solution vectors into

several subcomponents was proposed by (Potter and

Jong, 1994). The approach proposed by Potter and

Jong (CCGA) decomposes a n-dimensional

optimization problem into n one-dimensional

problems (one for each variable). The CCGA

employs CC framework and the standard GA. Potter

and Jong had investigated two different modification

of the CCGA: CCGA-1 and CCGA-2. The CCGA-1

evolves each variable of objective in a round-robin

fashion using the current best values from the other

variables of function. The CCGA-2 algorithm

employs the method of random collaboration for

calculating the fitness of an individual by integrating

it with the randomly chosen members of other

subcomponents. Potter and Jong had shown that

CCGA-1 and CCGA-2 outperforms the standard GA.

The following pseudocode presents general CC

stages:

Pseudocode of Cooperative Coevolution

1: Decompose objective vector into m

smaller subcomponents;

2: i = 1;

3: while i < m do

Optimize i-th subcomponents with

EA, i = i + 1;

4: If termination condition is not

achieved then go to Step 2, else go

to Step 5;

5: Return best_solution.

The CC method is used for a wide range of real-

world applications ((Barrière and Lutton, 2009),

(García-Pedrajas et al, 2003) and (Liu et al, 2001)).

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

262

3 PROPOSED APPROACH

We have analyzed pros and cons of grouping-based

methods and DE-based approached, and have

proposed a new EA for solving large-scale global

optimization problems. The main idea of the

proposed search algorithm is to combine of an

original method of grouping variables for the CC with

problem decomposition strategy with the self-

adaptive DE (SaNSDE). The choice of the self-

adaptive approach is necessary as we have no any

information on a dependence between variables.

Thus, parameters of the search algorithms should be

adapted during the optimization process as

information about the grouping quality becomes

available.

As it is known, the CC approach can be efficient

only if the grouping of variables is correct. As shown

in (Omidvar et al, 2014), the learning dynamic

grouping is not able to divide variables into correct

subcomponents for many LSGO problems.

In the proposed approach, the grouping of

variables is random and adaptive. In the approach, the

number of grouped variables is equal for each

subcomponent. Such limitation excludes the

following problems:

- uneven distribution of computational

resources between search algorithms

(population sizes of EAs for each

subcomponent).

- tuning minimum and maximum numbers of

variables into group.

The proposed method of grouping (RAG (random

adaptive grouping)) works as follows. The n-

dimensional solution vector is divided into m s-

dimensional sub-components (m x s = n). We

randomly group variables into groups of equal sizes

using the uniform distribution. As we need to estimate

the quality of the distribution of variables, we will

perform the EA run within the predefined budget T of

the fitness function evaluation (each EA optimizes its

corresponding subcomponent). After that, we will

choose m/2 subcomponents with the worse

performance and randomly mix indices of its

variables. Finally, we will reset all EA parameters for

the worst m/2 sub-components after regrouping

variables. The reset is necessary because of the fact

that new grouping of variables defines a completely

different optimization problem.

The complete algorithm is called DECC-RAG.

The procedure of DECC-RAG can be descripted by

the following pseudo-code.

Pseudocode of DECC-RAG algorithm

1: Set FEV_global, T, FEV_local

= 0;

2: An n-dimensional object vector is

randomly divided into m

s-dimensional subcomponents;

3: Randomly mix indices of variables;

4: i = 1;

5: Evolve the i-th subcomponent with

SaNSDE algorithm;

6: If i < m, then i++, and go to Step

5 else go to Step 7;

7: Choose the best_solution

for each

subcomponents;

8: If (FEV_local < T) then go to Step

4 else go to Step 9;

9: Choose m/2 subcomponents with the

worse performance and randomly mix

indices of its subcomponents, restart

parameters of SaNSDE in these m/2

subcomponents, FEV_local = 0;

10: If (FEV>0) go to Step 4, else go

to Step 11;

11: Return the best solution.

4 EXPERIMENTAL SETTINGS

AND RESULTS

We have evaluate the performance of DE, SaNSDE

and the proposed DECC-RAG algorithm on the 20

LSGO benchmark problems provided within the

CEC’10 special session on Large Scale Global

Optimization (Ke et al, 2010). These benchmark

problems have been specially endowed with the

properties that real-world problems have.

The performance of DECC-RAG algorithm was

also compared with other well-known state-of-the-art

LSGO algorithms such as DMS-L-PSO (dynamic

multi-swarm and local search based on PSO

algorithm) (Liang and Suganthan, 2005), DECC-G

(cooperative coevolution with random dynamic

grouping based on differential evolution) (Yang et al,

2008c), MLCC (Multilevel cooperative coevolution

based on differential evolution) (Yang et al, 2008a)

and DECC-DG (cooperative coevolution with

differential grouping based on differential evolution)

(Omidvar et al, 2014). More detailed experimental

results for DMS-L-PSO, DECC-G, MLCC and

DECC-DG can be found in (Yang et al, 2017).

The DECC-RAG algorithm settings are: NP = 50

(population size for each subcomponent), m = 10 and

T = 3x10

. T is a parameter that represents a number

of FEVs (function evaluations) before the stage of

randomly mixing of the worse m/2 subcomponents.

A Novel Method for Grouping Variables in Cooperative Coevolution for Large-scale Global Optimization Problems

263

All experimental settings are as proposed in the

rules of the CEC’10 LSGO competition were used for

experiments:

- dimensions for all problem are D = 1000;

- 25 independent runs for each benchmark

problem;

- 3x10

fitness evaluations in each independent

run of algorithm;

- the performance of algorithms is estimated

using the median value of the best found

solutions.

We have implemented the proposed approach and

DE and SaNSDE algorithms with С++ language. As

it is known, LSGO problems are computationally

expensive. The Table 1 shows the runtime of 10000

fitness evaluations for each benchmark problem using

1 thread of the AMD Ryzen 7 1700x processor.

We have implemented all our numerical

experiments using the OpenMP framework for

parallel computing with 16 threads, where each

thread was allocated for one benchmark problem.

Figure 1 demonstrate the calculation time (in hours)

of all benchmark problems with 16 threads and with

1 thread. As we can see from Figure 1, the calculation

time for the fitness function was reduced 5.9 times.

The results of 25 independent runs are presented

in Table 2. The first column contains the benchmark

problem number, the next columns contain mean

performance for all investigated algorithms. There are

two values in each cell: median value and standard

deviation of the best-found solutions obtained with 25

independent runs. The last row of the Table 2 contains

ranks for all algorithm averaged over all benchmark

problems. The rank of an algorithm is defined by the

median value, smaller median value defines smaller

rank.

Table 3 and Table 4 show results of Mann–

Whitney U test of statistical significance in the results

of 25 independent runs for DECC-RAG vs DE and

DECC-RAG vs SaNSDE, respectively. The

calculation of p-values has been performed using the

R language in the R-studio software. We use the

following notations in Tables 3 and 4: the sign “<”

means that for the current pair of algorithms, the first

algorithm outperforms the second one, otherwise the

sign “>” is used, and the sign “≈” is used when there

is no statistical significant difference in the results.

The p-value for all tests was equal to 0.05.

Figures 2, 3, 4, 5 and 6 demonstrate the dynamic

of the average performance (25 independent runs) of

DE, SaNSDE and the DECC-RAG algorithms for

some benchmark problems. The bottom axis contains

the number of the fitness function evaluations, and the

vertical axis contains the average value of the fitness

function.

As we can see from the results from Table 2, the

proposed DECC-RAG algorithm outperforms on

average some state-of-art algorithms such as DMS-L-

PSO, DECC-G, MLCC and DECC-DG.

Figures 2-6 show that the DECC-RAG provides

better average fitness value that the classical DE and

the standard SaNSDE algorithms do.

The statistical significance of differences in the

results for DECC-RAG vs SaNSDE was not observed

only on the 6-th benchmark problem.

We have estimated the performance of the DECC-

RAG for different sizes of subcomponents, and can

conclude that the best performance is obtained with

the number of groups equal to 10 (m = 10).

5 CONCLUSIONS

In this study, we have proposed a new EA for large-

scale global optimization problems. The approach

uses an original random adaptive grouping method

for cooperative coevolution framework.

We have tested the proposed DECC-RAG

algorithm on the representative set of 20 benchmark

problems from the CEC’10 LSGO special session and

competition, and have compared the results of the

numerical experiments with other state-of-art

techniques. The experimental results have shown that

the DECC-RAG outperforms on average DMS-L-

PSO, DECC-G, MLCC and DECC-DG algorithms.

The issues needed to be further studied are:

- design more effective self-adaptive method of

grouping variables based on randomness;

- improve performance of SaNSDE algorithm

for more effective use in cooperative

coevolution framework to solve LSGO

problems.

In further work, we will provide more detailed

analysis of the DECC-RAG parameters and will

estimate the performance of the DECC-RAG with

other benchmark problems for higher dimensions. We

will also try alternative random grouping strategies.

ACKNOWLEDGEMENTS

This research is supported by the Ministry of

Education and Science of Russian Federation within

State Assignment № 2.1676.2017/ПЧ.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

264

REFERENCES

Bäck, T. (1996) Evolutionary Algorithms in Theory and

Practice: Evolution Strategies, Evolutionary

Programming, Genetic Algorithms, Science.

Barrière, O. and Lutton, E. (2009) ‘Experimental analysis

of a variable size mono-population cooperative-

coevolution strategy’, in Studies in Computational

Intelligence, pp. 139–152. doi: 10.1007/978-3-642-

03211-0_12.

Brest, J., Zumer, V. and Maucec, M. S. (2006) ‘Self-

Adaptive Differential Evolution Algorithm in

Constrained Real-Parameter Optimization’, 2006 IEEE

International Conference on Evolutionary

Computation, pp. 215–222. doi: 10.1109/CEC.2006.16

88311.

Gagn, C. (2012) ‘DEAP : Evolutionary Algorithms Made

Easy’, Journal of Machine Learning Research, 13, pp.

2171–2175. doi: 10.1.1.413.6512.

García-Pedrajas, N., Hervás-Martínez, C. and Muñoz-

Pérez, J. (2003) ‘COVNET: A cooperative

coevolutionary model for evolving artificial neural

networks’, IEEE Transactions on Neural Networks,

14(3), pp. 575–596. doi: 10.1109/TNN.2003.810618.

Jiang, B. and Wang, N. (2014) ‘Cooperative bare-bone

particle swarm optimization for data clustering’, Soft

Computing, 18(6). doi: 10.1007/s00500-013-1128-1.

Ke, T., Xiaodong, L., P. N., S., Zhenyu, Y., Thomas, W.,

(2010) ‘Benchmark Functions for the CEC’2010

Special Session and Competition on Large-Scale

Global Optimization’. Technical report, Univ. of

Science and Technology of China 1–23.

Liang, J. J. and Suganthan, P. N. (2005) ‘Dynamic multi-

swarm particle swarm optimizer’, in Proceedings -

2005 IEEE Swarm Intelligence Symposium, SIS 2005,

pp. 127–132. doi: 10.1109/SIS.2005.1501611.

Lin, L., Gen, M. and Liang, Y. (2014) ‘A hybrid EA for

high-dimensional subspace clustering problem’, in

Proceedings of the 2014 IEEE Congress on

Evolutionary Computation, CEC 2014, pp. 2855–2860.

doi: 10.1109/CEC.2014.6900313.

Liu, Y. et al. (2001) ‘Scaling up fast evolutionary

programming with cooperative coevolution’, in

Proceedings of the 2001 Congress on Evolutionary

Computation (IEEE Cat. No.01TH8546), pp. 1101–

1108. doi: 10.1109/CEC.2001.934314.

Mei, Y., Li, X. and Yao, X. (2014) ‘Variable neighborhood

decomposition for Large Scale Capacitated Arc

Routing Problem’, in Proceedings of the 2014 IEEE

Congress on Evolutionary Computation, CEC 2014, pp.

1313–1320. doi: 10.1109/CEC.2014.6900305.

Omidvar, M. N. et al. (2014) ‘Cooperative co-evolution

with differential grouping for large scale optimization’,

IEEE Transactions on Evolutionary Computation,

18(3), pp. 378–393. doi: 10.1109/TEVC.2013.22

81543.

Potter, M. A. and Jong, K. A. (1994) ‘A cooperative

coevolutionary approach to function optimization’, pp.

249–257. doi: 10.1007/3-540-58484-6_269.

Potter, M. A. and Jong, K. A. De (2000) ‘Cooperative

Coevolution: An Architecture for Evolving Coadapted

Subcomponents’, Evolutionary Computation, 8(1), pp.

1–29. doi: 10.1162/106365600568086.

Storn, R. and Price, K. (1995) ‘Differential Evolution - A

simple and efficient adaptive scheme for global

optimization over continuous spaces’, Technical report,

International Computer Science Institute, (TR-95-012),

pp. 1–15. doi: 10.1023/A:1008202821328.

Yang, Q. et al. (2017) ‘A Level-based Learning Swarm

Optimizer for Large Scale Optimization’, IEEE

Transactions on Evolutionary Computation. doi:

10.1109/TEVC.2017.2743016.

Yang, Z., Tang, K. and Yao, X. (2008a) ‘Multilevel

cooperative coevolution for large scale optimization’,

in 2008 IEEE Congress on Evolutionary Computation,

CEC 2008, pp. 1663–1670. doi: 10.1109/CEC.2008.46

31014.

Yang, Z., Tang, K. and Yao, X. (2008b) ‘Self-adaptive

differential evolution with neighborhood search’, in

2008 IEEE Congress on Evolutionary Computation,

CEC 2008, pp. 1110–1116. doi: 10.1109/CEC.2008.46

30935.

Yang, Z., Tang, K. and Yao, X. (2008c) ‘Large scale

evolutionary optimization using cooperative

coevolution’, Information Sciences, 178(15), pp. 2985–

2999. doi: 10.1016/j.ins.2008.02.017.

APPENDIX

Table 1: Runtime of 10000 FEs (in seconds) on the CEC’10 LSGO benchmark problems.

Func. № F1 F2 F3 F4 F5 F6 F7 F8 F9 F10

Time 0.396 0.209 0.21 0.52 0.334 0.34 0.309 0.307 1.312 1.134

Func. № F11 F12 F13 F14 F15 F16 F17 F18 F19 F20

Time 1.139 0.112 0.126 2.219 2.016 2.04 0.077 0.133 0.072 0.1

A Novel Method for Grouping Variables in Cooperative Coevolution for Large-scale Global Optimization Problems

265

Table 2: Experimental results on the CEC’10 LSGO benchmark problems.

№ func. DECC-RAG DE SaNSDE DMS-L-PSO DECC-G MLCC DECC-DG

F1 2.69E-18 4.19E+08 2.00E+04 1.61E+07 3.53E-07 1.66E-14 1.42E+02

5.10E-18 2.75E+08 2.04E+06 1.41E+06 1.44E-07 2.97E-12 4.66E+04

F2 7.33E+02 7.38E+03 2.80E+03 5.53E+03 1.32E+03 2.43E+00 4.46E+03

7.52E+01 3.02E+02 1.67E+02 5.38E+02 2.55E+01 1.52E+00 1.87E+02

F3 1.64E+00 1.95E+01 1.47E+01 1.56E+01 1.14E+00 6.24E-10 1.66E+01

1.77E-01 8.60E-02 4.31E-01 1.08E-01 3.35E-01 1.12E-06 3.02E-01

F4 9.50E+11 8.78E+12 2.82E+12 4.32E+11 2.46E+13 1.78E+13 5.08E+12

3.50E+11 3.43E+12 1.01E+12 8.05E+10 8.14E+12 5.47E+12 1.89E+12

F5 1.54E+08 7.96E+07 9.00E+07 9.35E+07 2.50E+08 5.11E+08 1.52E+08

4.41E+07 2.12E+07 8.22E+06 9.04E+06 6.84E+07 1.07E+08 2.15E+07

F6 2.04E+01 2.09E+01 1.27E+06 3.66E+01 4.71E+06 1.97E+07 1.64E+01

5.75E+06 6.84E+06 8.12E+05 1.21E+01 1.03E+06 4.37E+06 3.45E-01

F7 2.90E+02 3.08E+08 1.90E+05 3.47E+06 6.57E+08 1.15E+08 9.20E+03

8.22E+02 1.76E+08 6.18E+04 1.16E+05 5.40E+08 1.45E+08 1.26E+04

F8 1.78E+07 2.53E+08 8.16E+06 2.02E+07 9.06E+07 8.82E+07 1.62E+07

7.43E+08 3.88E+08 2.22E+07 1.88E+06 2.64E+07 3.40E+07 2.63E+07

F9 6.17E+07 5.56E+08 2.31E+08 2.08E+07 4.35E+08 2.48E+08 5.52E+07

8.72E+06 8.20E+07 9.95E+07 1.58E+06 4.87E+07 2.16E+07 6.45E+06

F10 3.25E+03 7.72E+03 9.40E+03 5.09E+03 1.02E+04 3.97E+03 4.47E+03

1.88E+02 2.47E+02 2.82E+02 4.26E+02 3.13E+02 1.45E+03 1.29E+02

F11 2.16E+02 1.88E+02 1.74E+02 1.68E+02 2.59E+01 1.98E+02 1.02E+01

1.31E+01 6.40E+00 1.51E+01 1.90E+00 1.73E+00 1.12E+00 8.71E-01

F12 8.88E+03 5.59E+05 4.03E+05 2.83E+01 9.69E+04 1.01E+05 2.58E+03

1.15E+03 6.91E+04 4.83E+04 9.88E+00 9.55E+03 1.57E+04 1.08E+03

F13 1.56E+03 1.01E+09 2.52E+04 1.03E+05 4.59E+03 2.12E+03 5.06E+03

3.81E+03 6.79E+08 1.61E+05 6.18E+04 4.16E+03 4.70E+03 3.65E+03

F14 2.01E+08 1.60E+09 7.78E+08 1.25E+07 9.72E+08 5.71E+08 3.46E+08

2.07E+07 1.52E+08 1.28E+08 1.62E+06 7.52E+07 5.50E+07 2.42E+07

F15 5.16E+03 7.75E+03 1.06E+04 5.48E+03 1.24E+04 8.67E+03 5.86E+03

3.60E+02 2.55E+02 4.34E+02 3.46E+02 8.24E+02 2.07E+03 1.05E+02

F16 4.13E+02 3.77E+02 3.73E+02 3.18E+02 6.92E+01 3.96E+02 7.50E-13

3.05E+01 4.32E+00 1.12E+01 2.04E+00 6.43E+00 5.76E+01 6.25E-14

F17 1.68E+05 1.04E+06 8.68E+05 4.75E+01 3.11E+05 3.47E+05 4.02E+04

1.17E+04 7.94E+04 6.84E+04 1.15E+01 2.24E+04 3.11E+04 2.29E+03

F18 4.96E+03 4.15E+10 5.83E+05 2.50E+04 3.54E+04 1.59E+04 1.47E+10

6.35E+03 1.70E+10 1.81E+08 1.10E+04 1.53E+04 9.48E+03 2.03E+09

F19 2.23E+06 2.96E+06 1.93E+06 2.03E+06 1.14E+06 2.04E+06 1.75E+06

1.93E+05 4.01E+05 1.89E+05 1.41E+05 6.23E+04 1.42E+05 1.10E+05

F20 1.84E+03 5.25E+10 2.80E+05 9.82E+02 4.34E+03 2.27E+03 6.53E+10

5.04E+02 1.58E+10 1.37E+07 1.40E+01 8.25E+02 2.26E+02 6.97E+09

Average

Rank

2.8 5.85 4.3 3.15 4.5 4.2 3.2

Table 3: Results of Mann–Whitney U test for DECC-RAG vs DE.

< < < < > < < < < <

> < < < < > < < < <

Table 4: Results of Mann–Whitney U test for DECC-RAG vs SaNSDE.

< < < < > ≈ < > < <

> < < < < > < < > <

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

266

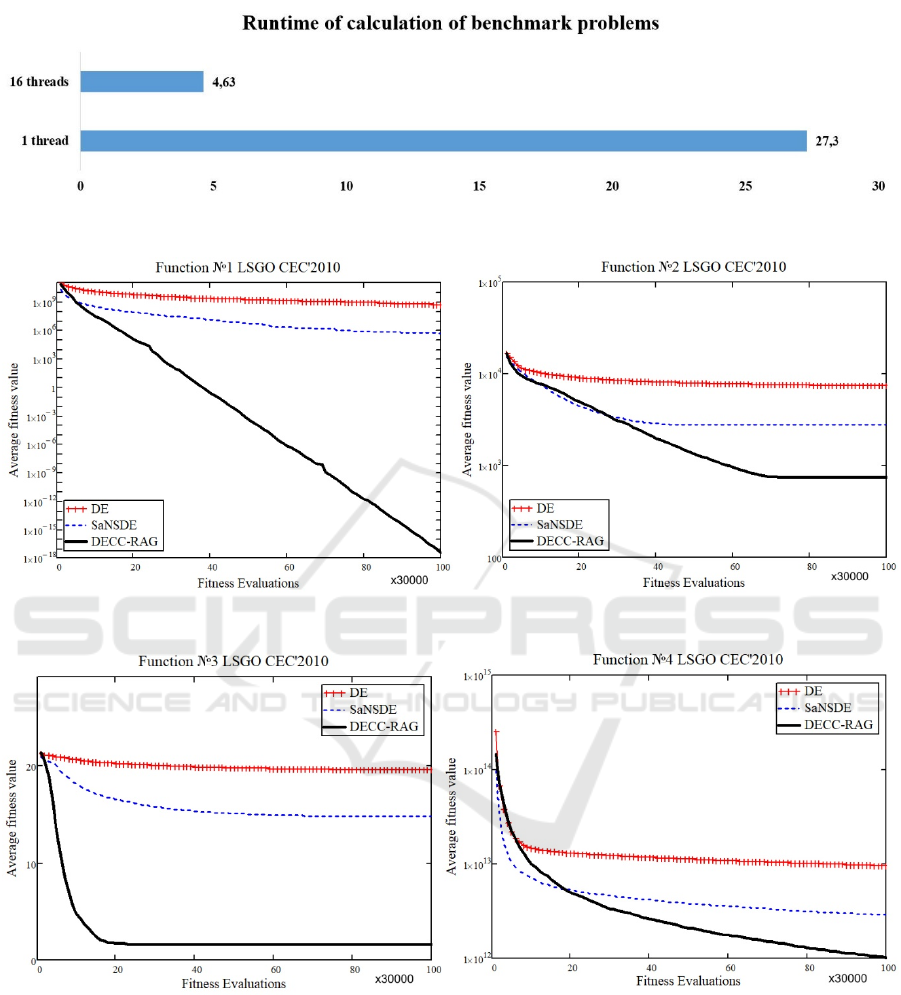
Figure 1: Runtime (in hours) for CEC’10 LSGO benchmark problems using 1 thread and 16 threads.

Figure 2: The average performance for F1 and F2 problems.

Figure 3: The average performance for F3 and F4 problems.

A Novel Method for Grouping Variables in Cooperative Coevolution for Large-scale Global Optimization Problems

267

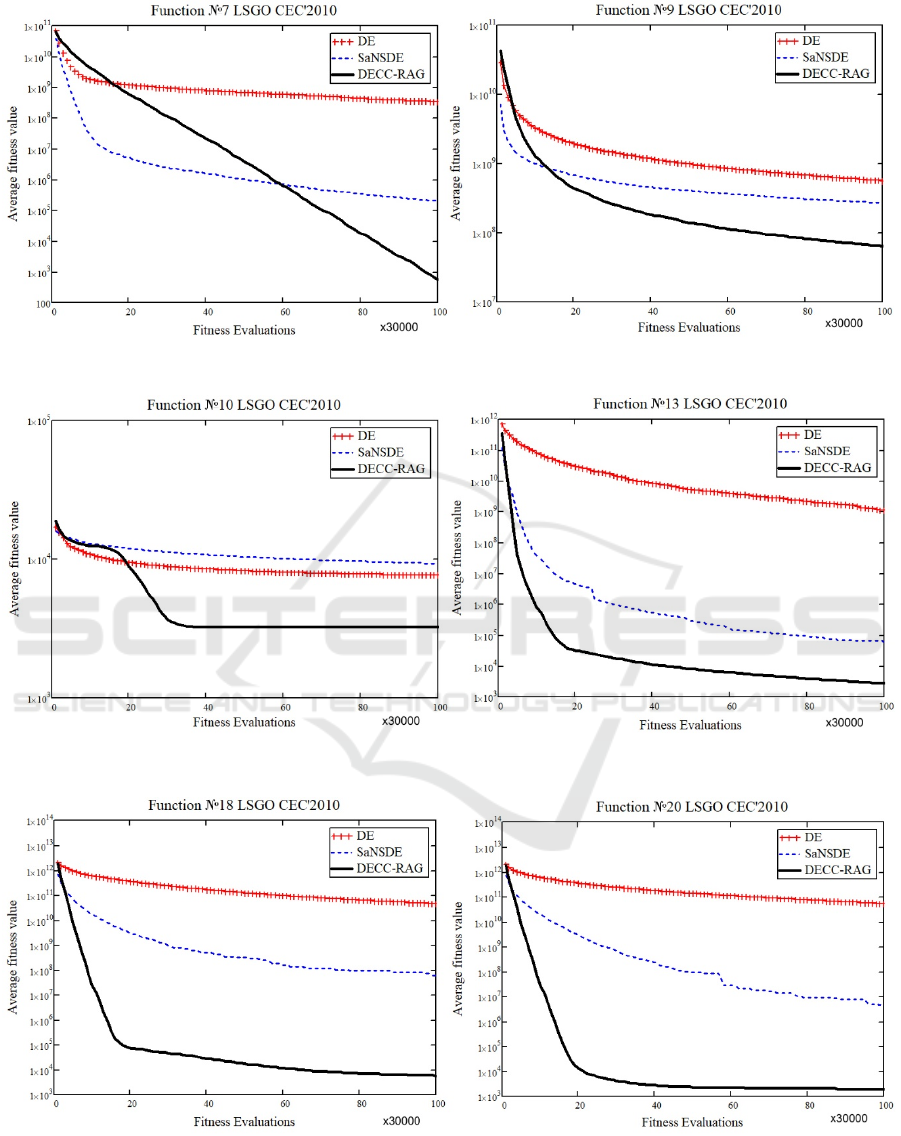
Figure 4: The average performance for F7 and F9 problems.

Figure 5: The average performance for F10 and F13 problems.

Figure 6: The average performance for F18 and F20 problems.

ICINCO 2018 - 15th International Conference on Informatics in Control, Automation and Robotics

268