An Efficient Decentralized Multidimensional Data Index: A Proposal

Francesco Gargiulo

, Antonio Picariello

and Vincenzo Moscato

Italian Aerospace Research Centre, via Maiorise, Capua (CE), Italy

Department of Computing, University Federico II of Napoli, Napoli, Italy

Keywords: Distributed Index, Large Databases, Multidimensional Data Index, Decentralized K-Nearest Neighbour

Query.

Abstract: The main objective of this work is the proposal of a decentralized data structure storing a large amount of data

under the assumption that it is not possible or convenient to use a single workstation to host all data. The

index is distributed over a computer network and the performance of the search, insert, delete operations are

close to the traditional indices that use a single workstation. It is based on k-d trees and it is distributed across

a network of "peers", where each one hosts a part of the tree and uses message passing for communication

between peers. In particular, we propose a novel version of the k-nearest neighbour algorithm that starts the

query in a randomly chosen peer and terminates the query as soon as possible. Preliminary experiments have

demonstrated that in about 65% of cases it starts a query in a random peer that does not involve the peer

containing the root of the tree and in the 98% of cases it terminates the query in a peer that does not contain

the root of the tree.

1 INTRODUCTION

A multidimensional data index is a building block for

a variety of applications based on Linked open Data

(LOD) and Big Data. The LOD paradigm is gaining

increased attention in recent years and the size of the

phenomenon is considerable, we are talking about

hundreds of millions of information published in the

form of ”concepts” and of billions of connections

between these concepts (Abele, 2017). It is

reasonable to assume the proliferation of new

applications and new services that are able to take

advantage of this huge quantity of information.

Big Data is a term for data sets that are so large or

complex that traditional data processing software

applications are inadequate to deal with them. The

proposed index fits the requirements of LOD and Big

Data applications.

A decentralized multidimensional data index also is

suitable for sensor networks because they could

collect a very large amount of multidimensional data

(position, timestamp, temperature, pressure, etc.).

Often a subset of the nodes of the network can

manage a network connection, execute software and

store data, therefore the sensor network, through these

nodes, may implement itself the index.

Finally, a multidimensional data index is also

appropriate for text indexing. After the extraction of

a set of concepts C from the text (Basile, 2007) and

the introduction of a similarity measures d between

them, e.g. Resnik, Leacock & Chodorow, Wu &

Palmer (Corley, 2005), it is possible to build a metric

space (C, d). Well known mapping algorithms, such

as FastMap (Faloutsos, 1995) or MDS (Kruskal,

1978), calculate a mapping between this metric space

and a new vector space. The resulting points in this

vector space populates an instance of the

multidimensional data index as proposed in this work.

Range query and k-nearest on this data structure

query will return concepts that are also semantically

close concepts (with respect the similarity measure

chosen). A non-trivial example based on this

approach for a semantic driven requirements

consistency verification is (Gargiulo, 2015).

2 RESEARCH IDEAS AND

RESULTS

This section introduces the problem description and

our proposal to cope with it.

Gargiulo, F., Picariello, A. and Moscato, V.

An Efﬁcient Decentralized Multidimensional Data Index: A Proposal.

DOI: 10.5220/0006851202310238

In Proceedings of the 7th International Conference on Data Science, Technology and Applications (DATA 2018), pages 231-238

ISBN: 978-989-758-318-6

231

2.1 Problem Description

Suppose we have a k-d tree “big enough” that cannot

be handled with a single workstation. If we want to

distribute it over a network of peers we need an

allocation strategy that maps the set of nodes of the

tree to the set of peers. Suppose that this mapping

allocates the nodes of the tree to the peer 



,



and

that all edges of the tree are preserved. Of course,

there are internal edges (i.e. edges connecting nodes

in the same peer) and crossing edges (i.e. edges

connecting nodes in different peers). From a logical

point of view, it is possible to reuse the well-know

(efficient) searching algorithms because all original

edges of the tree are available, it does not matter

whether they are internal or crossing edges. In

practice, crossing edges must be managed in a special

way because the current peer 



cannot process a node

hosted in another peer 



. In this case, 



can only

delegate to 



the elaboration of the remaining part of

the query sending to it the current partial result. From

now on, 



waits for a response from 



and, in the

meantime, it can process the next query. This

approach has advantages and disadvantages. On one

side, the number of points stored in a set of peers is

greater than the number of points stored on a single

peer and roughly the well-known search algorithms

can be reused. In addition, multiple queries run in a

parallel way. In fact, the number of initiated queries

is potentially limitless even if the number of peers

limits the number of the running queries. On the other

side, the peer containing the root of the tree is the only

entry point for all the new queries and it is the only

exit point for all the responses. This is the main

drawback and without an accurate message priority

management the throughput of this naive distributed

k-d tree can be worse than a traditional k-d tree. It is

interesting to note that this behaviour does not depend

on the allocation strategy because traditional search

algorithms always start and terminate the elaboration

in the root node. Hence, the need for a novel

distributed search algorithm that starts a query in any

randomly chosen node/peer and returns the correct

result as soon as possible without visiting the root

node.

2.2 Our Proposal

The proposal of a decentralized index for

multidimensional data relies on a distributed tree-

based data structure and a novel random k-nearest

neighbour algorithm, named R-KN.

In particular, we choose k-d tree (Samet, 2006) as

the data structure to extend. The novel R-KN

algorithm resembles the well-known random k-

nearest neighbour (KN) algorithm, but R-KN starts

in a random node of the tree and it relies on the

following assertions:

a) If the R-KN starts the elaboration from a node

visited also by KN, with a little adjustment of the

node status management, the R-KN returns the

correct result.

b) Starting from a randomly chosen node it is easy

to find a node visited by the KN algorithm near

to it (SNP-Starting Node Property).

c) If the R-KN stops the elaboration of the current

query  in a special node, named ending node for

q, the R-KN returns the correct result (ENP-

Ending node property).

The R-KN algorithm is the main contribution of

this work and it will be described in detail below

(Gargiulo, 2017). The following section describes the

distributed data structure.

2.2.1 The Distributed Data Structure

From the logical point of view, the data structure is a

k-d tree. In k-d trees each level of the tree compares

against 1 dimension and each node  of the level has

a split value with respect to that dimension. An

internal node stores its splitting coordinate in

 and its split value in .

Internal nodes are only routing nodes and they do not

store data points; in particular, all multidimensional

points are stored in buckets located in the leaves of

the k-d tree (one bucket per leaf) as described in

(Samet, 2006) par. 1.5.1.4. The size of the bucket

does not play a central role, it is a constant value much

smaller than the total number of points stored in the

tree. The k-d tree nodes, by means of an allocation

strategy, are assigned to a set of peers 







. as

described in section 2.1. Even if the allocation

strategy is necessary in order to achieve the final data

structure, almost all strategies are good. This is

because the allocation strategy cannot affect the time

complexity of a search algorithm. In fact, the

searching algorithms follow the edges of the tree to

reach the next node to process. If the edge is a

crossing edge the current peer always hands over to

another peer. In the worst case, the allocation strategy

may be one to one mapping between node and peers

and therefore the number of hops is, at worse, equal

to the number of nodes processed by the algorithm.

Therefore, a search algorithm on distributed k-d

tree is as efficient as the search algorithm on k-d tree.

In practice, every single hop adds a delay due to the

network latency consequently a strategy that evenly

allocates nodes to peers is preferable.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

232

2.2.2 The Random K-Nearest Neighbour

Algorithm (R-KN)

For the purpose of describe the R-KN algorithm a

very brief description of the KN algorithm (Samet,

2006) may help. It alternates two phases: descending

and ascending phases. During the descending phase,

it selects the subtree to visit first (by comparing the

query point with the split value stored in the current

node); it sets the state of the node (e.g. leftSideVisited

or rightSideVisited) and it moves to the child of the

node. If the current node is a leaf, it adds the points

stored in its bucket to a temporary result list  of size

k. If the number of points in  exceeds k then the

algorithm discards the points further away from the

query point. During the ascending phase, if the other

subtree of the current node must be visited the KN

algorithm descends on it and it sets the state of the

node (e.g. bothSidesVisited). If there is no need to

visit the other subtree or the KN already visited both

subtrees the KN ascends to the parent of the current

node. If the current node is the root node the KN

terminates. Here it is useful to recall how the KN

algorithm decides whether to process the other sibling

during the ascending phase. When the algorithm

comebacks to  from one of its child, it checks a

condition that tells us if the other subtree of 

contains, or not, points that can be added to the

current temporary results of the query  







where p is the query point. Suppose that:  













is the farthest point in temporary result list

 from  













, and i = v.splitCoordinate, if:







 











 





(1)

Then the algorithm processes the other siblings

also otherwise the algorithm ignores the other sibling

(Samet 2006). Of course, we are implicitly assuming

also that the list  is full, otherwise the KN algorithm

always visits the other sibling in order to fill 

without evaluating (1). Therefore, the value  affects

the behaviour of the KN since if  is empty then the

other subtree will be always processed. As stated, the

R-KN starts its elaboration in a node visited by the

KN algorithm. The problem arises when R-KN

ascends to a parent node never visited because its

state is a null value. The «little adjustment»

mentioned before is the following: if the algorithm

ascends from a left (right) subtree and the state of the

parent node is null then it sets the state in order to

remember that the left (right) subtree was visited, e.g.

leftSideVisited (rightSideVisited).

The R-KN performs exactly the same steps of the

KN algorithm except that:

a) R-KN starts in a randomly chosen node

belonging to the set of nodes that the KN

visits during its execution;

b) R-KN performs the above node state

adjustment in its ascending phases.

Suppose that  is one of the two algorithm KN

and R-KN,  a k-nearest query for  and let Leaves(A,

q), Nodes(A, q) and Results(A, q) are respectively the

unordered sets of leaves, nodes processed by  with

query  and the result (the k-nearest points) of  with

query . The objective is to demonstrate that:

Theorem 1 (Correctness of R-KN algorithm):

For each query , if R-KN starts in a node n 

Nodes(KN, q)  Result(KN, q) = Result(R-KN, q).

Since these sets are unordered sets, let assume that

they are equal if and only if they contain the same

nodes regardless the order the nodes are listed.

Let first demonstrate two theorems:

Theorem 2: Leaves(KN, q) = Leaves(R-KN, q) 

Result(KN, q) = Result(R-KN, q).

Proof of theorem 2: The resulting data structure

is a list that stores the k-nearest neighbor points of the

point  regardless the order the nodes are processed.

Theorem 3: If R-KN starts in n  Nodes(KN, q)

 Nodes(R-KN, q) = Nodes(KN, q).

Proof of theorem 3: Suppose that n is not the root

since if R-KN starts in the root then the proof is

trivial. Therefore n can be an internal node or a leaf.

Suppose n is an internal node, i.e. n  Nodes(KN,

q) and n  Leaves(KN, q). If KN visits only one or

both of the children of n then R-KN does the same

because both KN and R-KN check the same

conditions (1) in node n. The difference between the

elaboration of KN and R-KN could be the order they

visit the children of n but this does not affect the

result. After, both KN and R-KN move its own

elaboration to the parent node m of n. Now, the

difference between KN and R-KN could be the status

the of the node m. In fact, if R-KN has never visited

m then it will check if the other child of m must be

visited. If KN already visited m and the other child of

m also then KN will move to the parent of m. R-KN

will visit the other child of m since KN did it and

because R-KN will check the same condition of KN.

Therefore, R-KN will visit the children of m in

reverse order with respect to KN but this does not

affect the result. At this point R-KN will move to the

parent of m as KN. The same reasoning can be applied

to the parent of m and so on up to the root. Therefore,

if n is an internal node then KN and R-KN visit the

same nodes. Finally, if n is a leaf then both KN and

R-KN in the next step will move the elaboration to the

parent node of n and the proof will proceeds as in the

An Efﬁcient Decentralized Multidimensional Data Index: A Proposal

233

previous case. Now, it is possible to demonstrate the

theorem 1.

Proof of theorem 1: Observing that if Node(KN,

q) = Nodes(R-KN, q)  Leaves(KN, q) = Leaves(R-

KN, q) the proof of theorem 1 follows from the

theorems 2 and 3.

Furthermore, the R-KN is as efficient as KN

because they visit exactly the same set of nodes and,

as stated above, the number of hops does not affect

the time complexity of R-KN. To complete the first

part of the description of the R-KN algorithm the next

question is: How do we find a node belonging to the

set of nodes visited by KN during its execution without

the need to execute it? The following property, named

Starting Node Property (SNP), helps to characterize

this kind of node.

2.2.3 The Starting Node Property (SNP) for

Binary Trees

For the sake of simplicity, the SNP for binary tree will

be presented first. Binary trees can be considered as

k-d trees with one dimension and all k-d tree

algorithms (insert, delete and search) apply to binary

tree also.

SNP for binary trees: Let  = {

,…



} be the

set of the nodes visited at least once by the KN

algorithm,  the query point,  a node. Consider the

following property:



    

    

(2)

If (2) holds    .

Where . and . are respectively the

minimum and the maximum values stored in the

bucket of the leaf ;  and  are

respectively the left and the right child of .

Proof of SNP for binary trees: Let  be an

internal node of the tree for which the (2) holds, then

in the buckets of the leaves of the subtree of  there

must be at least a point  that will be returned in the

result of the query . In fact, if the binary tree contains

the point  then  is stored in the subtree of . If the

tree does not contain  then the closest point to  is

stored in the subtree of . Therefore, since    the

algorithm does not return the correct result if it does

not visit the subtree of . If  is a leaf the proof is the

same. Given a query point , using the SNP property

a recursive algorithm can find a node    starting

from a randomly chosen node  of the tree as follows:

Procedure findStartingNode(r)

if holdsSNP(r) OR isRoot(r)

return r

else

findStartingNode(r.parent)

end if

End procedure

Where 







returns true if the SNP

property holds for . Simply, the findStartingNode

algorithm moves to the parent of the current node (if

it exists) if the SNP is not true. Of course, there is no

guarantee that it will stop before reaching the root. In

order to analyze the effectivity of the

findStartingNode algorithm it must be estimated how

many time on average it returns the root. Traversing

the root node depends on the value of query point 

and the chosen random node : if the leaf  with the

bucket containing  and the node  are in opposite

subtrees of the root then it is imperative to traverse

the root node. Instead, if they are in the same subtree

intuitively there is a good chance that

findStartingNode returns before reaching the root.

Please note that even if the set  depends on the

value of , the SNP does not depends on  since the

FindStartingNode algorithm try to find a node in the

path from the root to the bucket that should contain

the query point  In order to estimate such

probabilities, we compute the mean value on all

possible choices of:

 The query point  (all points stored in the tree);

 The random node  (all nodes in the tree);

 The bucket size  (5, 10, 20, 30 and 40).

Over a set of trees with size in the range of 512 to

32.768 nodes. Since in a balanced binary tree with 

nodes there are    



leaves then maximum total

number of points stored in the tree is    



The result shows that the findStartingNode

algorithm does not returns the root in about 34% of

cases.

The performance of the findStartingNode

algorithm can be by improved choosing the random

node with the following rule: given a query point,

choose a random node in the left subtree of the root if

p ≤ root.split otherwise, choose a random node in the

right subtree of the root. Please note that during the

construction of the tree, each node can be easily and

efficiently labelled as leftSideNode (rightSideNode) if

it belongs to the left (right) subtree of the root. In

practice, every new node simply inherits the label of

its parent. The results of tests of the findStartingNode

algorithm with this update are clearly better and it

returns a node other than the root in about 65% of

cases. The results still suggest the independence

between percentage and size of the trees.

Example 1: Let’s consider the binary tree in figure

1 with bucket size    and the query point   .

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

234

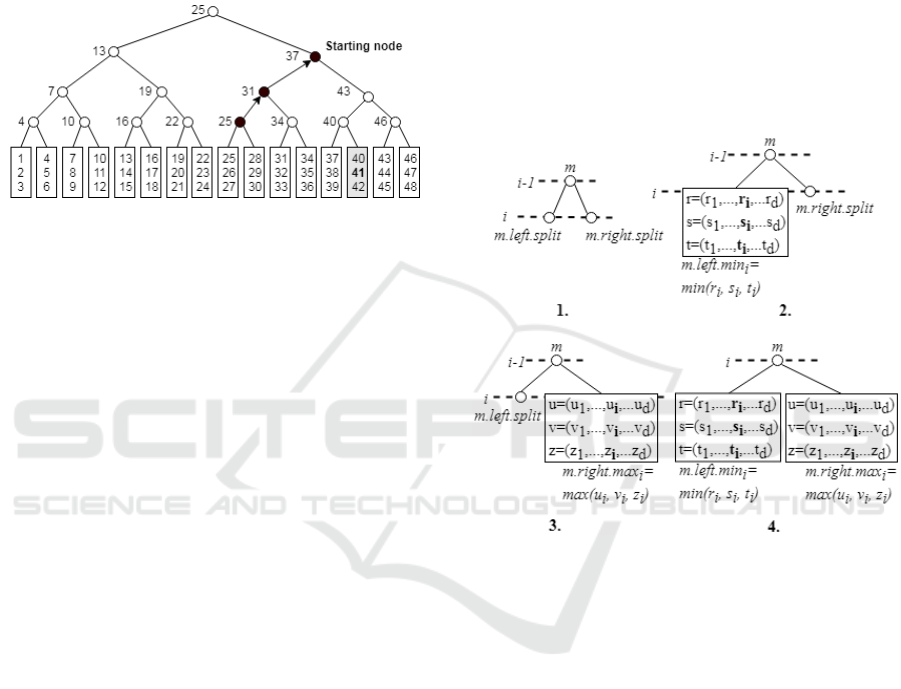
Let us suppose that the node 25 is the random

chosen node therefore the findStartingNode starts its

elaboration from it. Since, 







 

and 







 the algorithm moves to the

node 31. Again, both conditions are false and the next

node is 37. The findStartingNode returns the node 37

because 







 . Please note that the

point 41 belongs to a bucket in the subtree of node 37.

Figure 1: The starting node returned by findStartingNode

with the query point   and starting in the random

chosen node 25.

2.2.4 The Starting Node Property (SNP) for

K-D Trees

In order to affirm the SNP from k-d trees the

following definition needs:

Definition 1 (Stripe): Let   







 be a

query point and suppose that  is an internal node.

Consider the following conditions:

1. If both  and  are internal node

in the same level, they have the same splitting

coordinate i = m.left.splitCoordinate=

m.rightCoordinate (figure 2.1):

  



 

(3)

(If    swap them)

Here p

is the i-th coordinate of p.

2. If  is a leaf and  is internal i =

m.right.splitCoordinate (figure 2.2):





 



 

(4)

(If 



  swap them)

3. If  is a internal and  is leaf i =

m.left.splitCoordinate (figure 2.3):

  



 



(5)

(If   



swap them)

4. If both  and  are leaves i =

m.splitCoordinates (figure 2.4):





 



 



(6)

(If 



 



swap them)

Where 



(



) is the maximum

(minimum) value of the i-th coordinate of the points

contained in the bucket of . If one of the condition

(3), (4), (5) and (6) holds the node  is a stripe with

respect the i-th coordinate (i-stripe) for . In the

above definition the first three sub-condition

considers the cases in which at most one child of  is

an internal node. In these cases the split coordinate of

that child is used. Instead, in the last case both

children are leaves and the split coordinate of  itself

is used.

Figure 2: The four cases listed in the definition of the stripe

with respect the i-th coordinate (definition 1).

The SNP for k-d tree is the following:

SNP for k-d trees: Let  = {

,…, 

} the set

of the nodes visited at least once by the KN algorithm

on k-d tree and  













the query point.

If node  contains in its subtree a stripe for each

coordinate of     .

Proof of SNP for k-d trees: For the sake of

simplicity, suppose   , with higher number of

dimensions the proof is the same.

Let   







 be the query point. If the SNP

holds for a node  then there must exist two node 

and , such that they are respectively stripe for the x-

coordinate and y-coordinate. That is, minSplit

≤ p

≤

maxSplit

and minSplit

≤ p

≤ maxSplit

. Where

minSplit

(maxSplit

) is the value on the right (left)

side of one the inequalities (3), (4), (5) or (6).

Suppose, without loss of generality, that  as an

ancestor of . Since the subtree of  contains all

points having the x-coordinate in the range from

An Efﬁcient Decentralized Multidimensional Data Index: A Proposal

235

minSplit

to maxSplit

and the subtree of  contains

all points having the y-coordinate in the range from

minSplit

to maxSplit

then the subtree of  contains

 or the closest point to . If the KN does not visit 

it returns an incorrect result then    Since the

path from root to  contains both  and  then also

  . Let  be a randomly chosen node, the

findStartingNode algorithm for k-d trees is the same

as before except that it use the procedure

holdSNP4KD instead of holdSNP. The procedure

holdSNP4KD is the following:

Procedure holdsSNP4KD(n)

i = getCoordinateIndex()

if isStripe(n, i)

stripes[i] = true

if allStripes()

return true

end if

return false

End procedure

Where getCoordinateIndex() returns the i

coordinate as in the definition 1, stripes[] is an array

of boolean of size  and allStripes() returns true only

if all elements in stripes[] are true. Of course, all

elements of stripe are initialized to false.

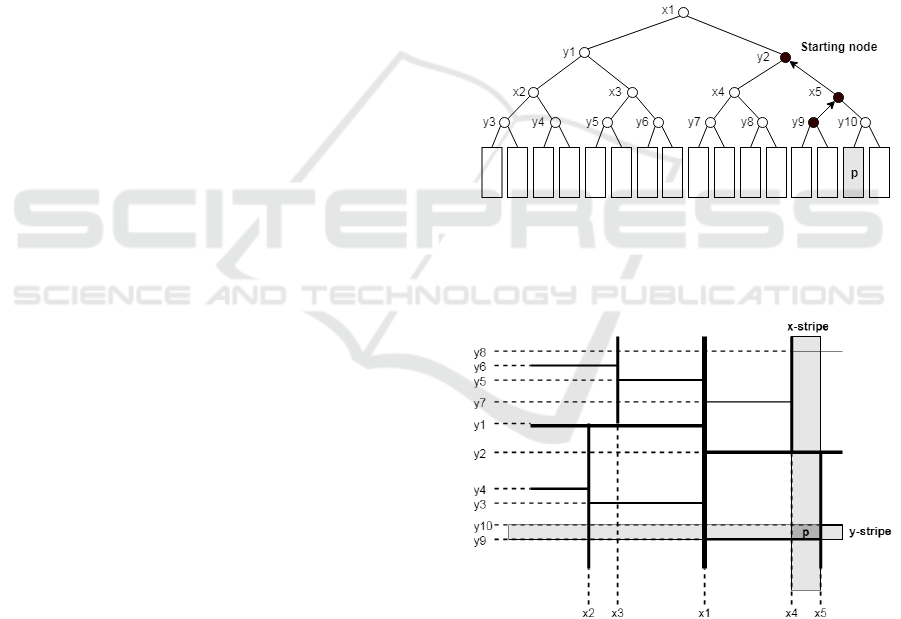
Example 2: Let’s consider the k-d tree in figure 3,

its planar representation in figure 4 and the query

point . Suppose that the chosen random node is .

Since, 







  then  it is not

a starting node for  and the algorithm moves to 

It is 







 , but since the (3)

holds then  is a y-stripe for  (figure 4) and the

algoritm sets stripes[0] = true. Because AllStripes =

false the algorithm moves to  and returns it as

starting node since  is a y-stripe for  and

AllStripes =true. The remaining part of the

description of the R-KN algorithm concerns the

condition to determine if a query has been completed

before reaching the root of the tree.

2.2.5 The Ending Node Property (ENP) for

Binary Trees

As already done for the Starting Node Property, first

the Ending Node Property for binary trees will be

introduced and it will be subsequently presented its

extension to k-d trees. Let  







be a query

having two oolean attibutes: q.leftSideComplete and

q.rightSideComplete.

The R-KN algorithm follows the rule: suppose during

the ascending phase the R-KN comebacks to the node

 from one of its children. If R-KN come from the left

(right) child of  and the right (left) subtree of  must

not be visited it set q.rightSideComplete = true

(q.leftSideComplete = true). If after the elaboration of

 it holds that both q.leftSideComplete and

q.rightSideComplete are true then  is an ending

node. In order to demonstrate that the R-KN can

terminate its elaboration in an ending node, we first

demonstrate that:

Theorem 4. Given a binary tree and a query  







. If the KN ascends to the node  from its left

child and the KN sets q.rightSideComplete = true

(q.leftSideComplete = true) in  then in the remaining

steps of the KN no other right (left) subtree will be

processed. Intuitively, a point stored in a leaf in a right

subtree of an ancestor of  is always more distant

from  than a point in a leaf belonging to the subtree

of . Therefore, if the KN does not process the right

subtree of , it does not process any right subtree of

the ancestors of .

Figure 3: The resulting starting node returned by the

findStartingNode with the random chosen node y9 and

query point p.

Figure 4: In the planar representation of the k-d tree, the

gray bands represents the two stripes obtained with the

findStartingNode starting in the random node y9. Note that

the point p resides in the intersection of the stripes.

Proof of therorem 4: Let  be the list of

temporary results and  the farthest point in  from

. Because the KN comes back from the left child of

 it holds that:

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

236

  

(7)

Furthermore, since q.rightSideComplete = true

then:



  







 



(8)

Please, note that p < v.split because if it is true

   then using (7) it holds that  

   and then



 







  



and

this contradicts (8). Now, suppose   , if

 is the right child of  then we must move to the

parent of  because  itself is the right subtree of 

and it was already processed. If  is the left child of 

then    by definition of binary tree.

Therefore, it holds that



 







 





it follows that the right subtree of  will not be

visited. Finally, since it is possible to apply the same

reasoning for each node in the path from  to the root

the conclusion is that no other right subtree will be

visited.

Theorem 5 (Correctness of the R-KN with ENP

for binary trees). Given a binary tree and a query ,

if the R-KN algorithm stops its elaboration in the first

ending node  it finds then it returns the correct

results to query.

Proof of theorem 5: Since  is an ending node

then the KN algorithm does not visit any other left

subtree nor right subtree along the path from  to the

root of the tree during the ascending phase (Theorem

4).

As for the SNP property, it is difficult calculate

exactly how many time the R-KN using ENP will

process the root. The same approach of SNP in order

to estimate the behavior of the R-KN algorithm is

used and in about 98% of cases the R-KN terminates

in a node other than the root.

Example 3: Let’s consider the binary tree in figure

5 and the query  







 . Suppose the R-

KN starts in the root node. During the first

descending phase it visits nodes 37, 31 and 34. It

processes the leaf with bucket containing the query

point    and it sets   . The R-KN

ascends to node 34 and it checks the (1) since  is

full. Since (1) holds, the algorithm process the other

sibling of 34 and it sets  







(it throws

away the points 35 and 36 that are so far away from

  ). Now, R-KN comes back to node 34 and

since it processed both its children then the R-KN

ascends to node 31 and checks the condition (1).

Since



  







  



then the left subtree of

node 31 must not be visited. Here, the R-KN sets

  . Intuitively, this

means that on the left side of the tree there are not

points belonging to the result of the query. Now, the

R-KN ascends to node 37 and again the condition (1)

is not true since



  







  



and the

algorithm sets   . The

node 37 is an ending node and the algorithm

terminates. Please note that if R-KN starts in node 37,

instead of at the root, it returns also the correct result

since node 37 is a starting node for .

Figure 5: The ending node returned by R-KN with the query

point p = 34. In its ascending phase, R-KN sets

q.leftSideComplete = true in node 31 and finally it sets

q.rightSideComplete = true in node 37.

2.2.6 The Ending Node Property (ENP) for

K-D Trees

Let  







be a query,  













a -

dimensional point and q.leftSideComplete(i) and

q.rightSideComplete(i) two boolean array of size d.

The R-KN algorithm follows the rule: suppose during

the ascending phase the R-KN comes back to the node

 from one of its children. If R-KN comes from the

left (right) child of  and the right (left) subtree of 

must not be visited it sets q.rightSideComplete(i) =

true (q.leftSideComplete(i) = true), where i =

v.splitCoordinate. If after the elaboration of  it holds

that q.leftSideComplete(i) and q.rightSideComplete(i)

are true for all coordinates, then  is an ending node.

Theorem 6 (Correctness of the R-KN with ENP

for k-dtrees). Given a k-d tree and a query  







where  













is a -dimensional point. If the

R-KN algorithm stops its elaboration in the first

ending node  it finds, then it returns the correct

results to query.

Proof of theorem 6: The demonstration follows

from the observation that the Theorem 4 holds if we

consider a single dimension. Since  is an ending

node, the Theorem 4 applies to all  coordinates and

then no other subtree will be processed in the

remaining steps of the algorithm.

An Efﬁcient Decentralized Multidimensional Data Index: A Proposal

237

3 RELATED WORKS

In the last decade multi-dimensional and high-

dimensional indexing in decentralized peer-to-peer

(P2P) networks, received extensive research

attention. In (Aly, 2011) there is proposal of a

distributed k-d tree based on MapReduce framework

(Dean, 2008). In such index structures queries are

processed similar to the centralized approach, i.e., the

query starts in root node and traverse the tree. These

methods exhibit logarithmic search cost, but face a

serious limitation. Peers that correspond to nodes

high in the tree can quickly become overloaded as

query processing must pass through them. In

centralized indexes this was a desirable property

because maintaining these nodes in main memory

allow the minimization of the number of I/O

operations. In distributed indexes it is a limiting factor

leading to bottlenecks. Moreover, this causes an

imbalance in fault tolerance: if a peer high in the tree

fails than the system requires a significant amount of

effort to recover. MIDAS (Tsatsanifos, 2013) is

similar to these works and in particular, MIDAS

implements a distributed k-d tree, where leaves

correspond to peers, and internal nodes dictate

message routing. MIDAS distinguishes the concepts

of physical and virtual peer. A physical peer is an

actual machine responsible for several peers due to

node departures or failures, or for load balancing and

fault tolerance purposes. A virtual peer in MIDAS

corresponds to a leaf of the k-d tree, and

stores/indexes all key-value tuples, whose keys reside

in the leaves rectangle and for any point in space,

there exists exactly one peer in MIDAS responsible

for it. Two algorithms for Nearest Neighbour Queries

are described: the first (expected 







) has low

latency and involve a large number of peers; the

second (expected 











) has higher latency but

involves far fewer peers. The proposed algorithms

process point and range queries over the

multidimensional indexed space in 







hops in

expectance.

4 CONCLUSIONS

The main objective of this work is the proposal of

index with the following characteristics: 1) Must be

used on a large amount of data. The assumption is that

it is not possible or convenient to use a single

workstation to host all the data; 2) It is distributed

over a computer network and ensures the greatest

possible benefits in terms of efficiency (search, insert,

delete), i.e. the performance are close to the

traditional indexes that use a single workstation. The

basic ideas behind are a data structure, called

Decentralized Random Trees (DRT), based on k-d

tree and a novel k-nearest neighbour algorithm,

named random k-nearest neighbour algorithm. The

Decentralized Random Trees represent the main

contribution of this work. With a DTR distributed

over a network of peers a randomly chosen peer can

start the propagation of a query in the network

without involving the peer containing the root of the

tree in about 65% of cases. Furthermore, the first peer

that determines that the search is complete will return

the result. With high probability, more than 98% of

cases, that peer is not the peer containing the root. Of

course, due the distributed nature of the DRT, more

than one query can be running at the same time. The

number of initiated queries is potentially limitless

even if the number of peers limits the number of the

running queries.

REFERENCES

Abele, A., McCrae, J.P., Buitelaar, P., Jentzsch, A.,

Cyganiak, R., 2017. Linking Open Data cloud diagram

2017. http://lod-cloud.net/

Corley, C., Mihalcea, R., 2005. Measuring the semantic

similarity of texts. In Proceedings of the ACL workshop

on empirical modeling of semantic equivalence and

entailment (pp. 13-18). Association for Computational

Linguistics.

Faloutsos, C., Lin, k., 1995. FastMap: A fast algorithm for

indexing, data-mining and visualization of traditional

and multimedia datasets, volume 24. ACM.

Kruskal, J.B., Wish, M., 1978. Multidimensional scaling,

volume 11. Sage.

Gargiulo, F., Gigante, G., Ficco, M., 2015. A semantic

driven approach for requirements consistency

verification. International. Journal of High Performance

Computing and Networking, 8(3):201–211.

Basile, P., De Gemmis, M., Gentile, A.L., Lops, P.,

Semeraro, G., 2007. Uniba: Jigsaw algorithm for word

sense disambiguation. In Proceedings of the 4th

International Workshop on Semantic Evaluations,

pages 398–401. Association for Computational

Linguistics.

Samet, H., 2006. Foundations of multidimensional and

metric data structures. Morgan Kaufmann.

Aly, M., Munich, M., Perona, P., 2011. Distributed k-d

trees for retrieval from very large image collections. In

British Machine Vision Conference, Dundee, Scotland.

Dean, J., Ghemawat, S., 2008. MapReduce: simplified data

processing on large clusters. Communications of the

ACM, 51(1):107–113.

Tsatsanifos, G., Sacharidis, D., Sellis, T., 2013. Index-

based query processing on distributed

multidimensional data. GeoInformatica 17.3 pages:

489-519.

DATA 2018 - 7th International Conference on Data Science, Technology and Applications

238