A Pooling Strategy for Flexible Repair Shop Designs

Hasan H

useyin Turan

, Shaligram Pokharel

, Andrei Sleptchenko

Tarek Y ElMekkawy

and Maryam Al-Khatib

School of Engineering and Information Technology, University of New South Wales, Canberra, Australia

Department of Mechanical and Industrial Engineering, College of Engineering Qatar University, Doha, Qatar

Department of Industrial and Systems Engineering, Khalifa University of Science and Technology, Abu Dhabi, U.A.E.

Keywords:

Spare Part Logistics, Repair Shop, Pooling, Heuristic.

Abstract:

We discuss the design problem of a repair shop in a single echelon repairable multi-item spare parts supply

system. The repair shop consists of several parallel multi-skilled servers, and storage facilities for the repaired

items. The effectiveness of repair shops and the total cost of a spare part supply system depend highly on

the design of repair facility and the management of inventory levels of the spare parts. In this paper, we

concentrate on a design scheme known as pooling. A repair shop can be considered as a pooled structure if the

spare parts can be divided into clusters such that each part type is unambiguously assigned to a single cluster

(cell). Nonetheless, it is both an important and tough combinatorial optimization question to determine which

type of spares to pool together. We propose a sequential solution heuristic to ﬁnd the best pooled design by

considering inventory allocation and capacity level designation of the repair shop. The numerical experiments

show that the suggested solution approach has a reasonable algorithm run time and yields considerable cost

reductions.

1 INTRODUCTION

Maintenance costs can constitute up to 60% of the

production costs of manufacturing ﬁrms (Keizer et al.,

2016). Therefore, thoughtful planning of mainte-

nance operations not only leads to a decrease in the

total cost but also signiﬁcant improvements in the reli-

ability of systems (L

opez-Santana et al., 2016). Main-

tenance planning includes the determination of the

maintenance strategy, time interval between mainte-

nance operations, and quantity and quality of main-

tenance resources such as technicians, supplies and

spare parts (Duffuaa, 2000). In this paper, the correc-

tive maintenance of high-valued assets in particular

decisions regarding the amount of spare part inven-

tory, capacity and design of repair facilities are ana-

lyzed.

The dominant inventory model for repairable

spare part is called METRIC (Multi-Echelon Tech-

nique for Recoverable Item Control), developed by

Sherbrooke (1968). The METRIC based models as-

sume that the repair capacity is inﬁnite. This assump-

tion may not be appropriate in most industrial set-

tings. Thus, some researchers have relaxed ample re-

pair capacity assumption (Diaz and Fu, 1997; Rap-

pold and Van Roo, 2009; Sleptchenko et al., 2003;

Srivathsan and Viswanathan, 2017).

The performance of repairable spare part system

also depends on the design of the repair facility. There

exist several different design alternatives for repair

shops. The two extreme situations are the dedi-

cated (no cross-training) and fully ﬂexible (full cross-

training) designs. In a dedicated design, each clus-

ter of servers is responsible for repairing a speciﬁc

spare part type. On the other hand, in a fully ﬂexi-

ble architecture all of the servers are merged into a

single cluster that serves all of the failed parts. Nev-

ertheless, in many real-life situations, cross-training

all servers to handle all failed item types may not be

feasible due to cost and/or quality penalties arising

from cross-training and/or scarcity of servers capable

of handling all of the item types (Tekin et al., 2009;

Qin et al., 2015).

Pooling is an intermediate level design between

the dedicated and fully ﬂexible systems. Pooling

means clustering of repairable items in the repair shop

by using some measure of similarity. In other words,

a repair shop has a pooled structure if the spare parts

272

Turan, H., Pokharel, S., Sleptchenko, A., Elmekkawy, T. and Al-Khatib, M.

A Pooling Strategy for Flexible Repair Shop Designs.

DOI: 10.5220/0006632502720278

In Proceedings of the 7th International Conference on Operations Research and Enterprise Systems (ICORES 2018), pages 272-278

ISBN: 978-989-758-285-1

can be divided into clusters such that each part type

is unambiguously assigned to a single cluster (cell).

Nonetheless, it is both an important and tough com-

binatorial optimization question to determine as to

which type of spares to pool together.

Even though pooling of resources are extensively

studied, to the best of our knowledge, no results

have been presented on pooled repair shops designs

in spare part supply systems integrated with capac-

ity decision. Thus, this study will contribute to the

current literature by addressing following fundamen-

tal issues: (i) how many clusters to pool; (ii) which

spare part types to pool together, and; (iii) how to as-

sign servers (capacity) to each cluster.

The rest of the paper is organized as follows. In

Section 2, problem deﬁnition and the mathematical

model are presented. The solution algorithm for the

proposed model is discussed in Section 3. Section 4

provides a computational study under different sce-

narios and input settings. Conclusions and future re-

search directions are summarized in Section 5.

2 PROBLEM DESCRIPTION AND

FORMULATION

The design problem of a repair shop in a single ech-

elon repairable multi-item spare part supply system

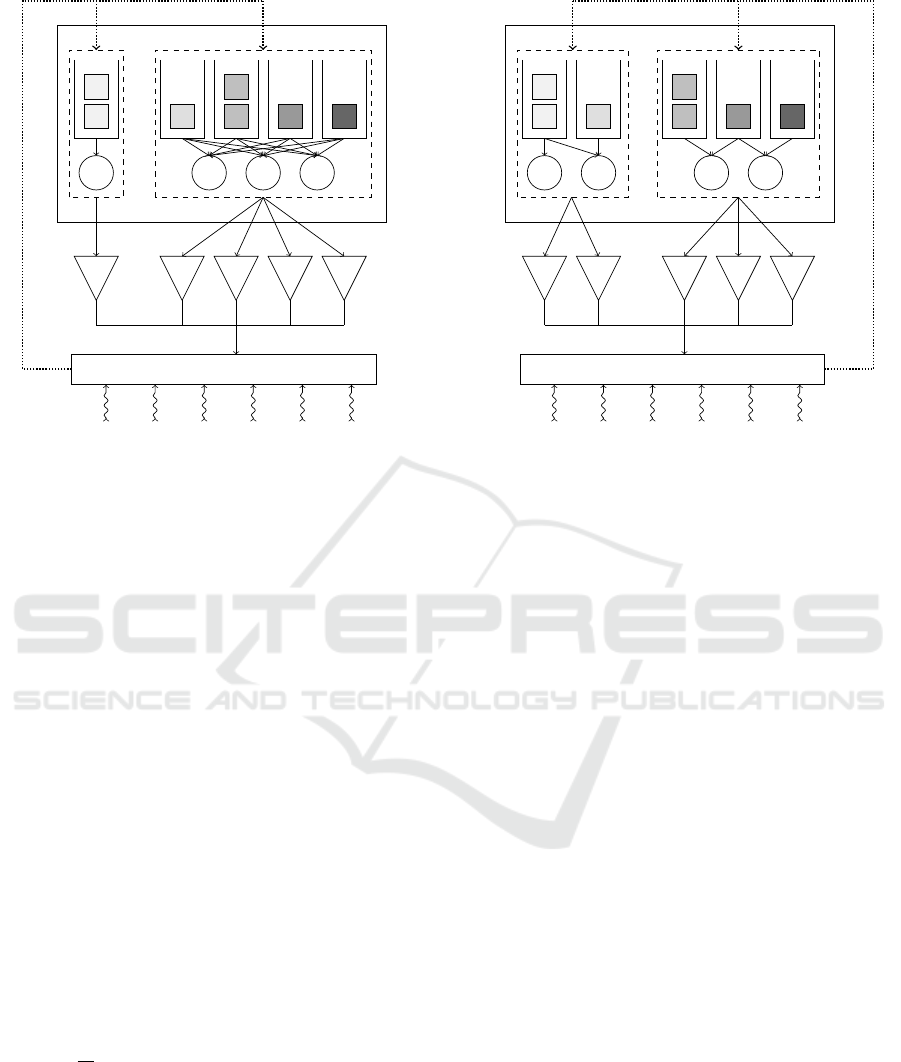
being considered here is illustrated in Figure 1. The

repair shop consists of several parallel multi-skilled

servers, and storage facilities for the repaired items.

Once a failed part received from technical system at

the installed base, it is queued to be served by a suit-

able server with the required skills. At the same time,

if a repaired (as-good-as-new) part is available in the

inventory, it is sent back to the installed base. If the

item is not available in the stock, the request is back-

ordered. In this case, the technical system goes down

and a downtime cost occurs till the requested ready-

for-use part is delivered.

The repair shop may have pooled structure with

one or more cells/clusters or an arbitrary structure. In

Figure 1(a), an example of a pooled repair shop with

ﬁve types of failed stock keeping units (SKUs), two

clusters and four servers is shown. The ﬁrst cluster

has a dedicated server with the ability to serve one

type of SKU. On the other hand, the second clus-

ter is obtained by pooling remaining four SKUs, and

this cluster has three cross-trained servers to serve all

(four) different types of repairables in that cluster. On

the other hand, in Figure 1(b), an arbitrary design is

presented, where the ﬁrst and the second clusters have

‘N’ and ‘W’ structures, respectively. It is should be

noted that in arbitrary designs, not all of the servers in

a cluster are fully ﬂexible; i.e., some servers are par-

tially cross-trained to repair only a subset of all SKUs

in the cluster. In this paper, we restrict design alterna-

tives limited to only pooled repair shops as in Figure

1(a), and formulate a stochastic mixed-integer mathe-

matical programming model to ﬁnd the minimum cost

spare part supply system. The sets, parameters and

decision variables for the developed formulations and

solution procedures are presented as follows.

Decision variables:

: Amount of initial inventory (basestock level)

kept on stock for SKU type i ( i = 1,...,N),

where S = (S

,. ..,S

: Number of the operational servers in the cluster

k (k = 1,. . .,y), and where Z = (z

,. ..,z

: Binary variable indicating that whether

the cluster k has a skill to repair SKU

type i( i = 1, ..., N) or not, where

= (x

,. ..,x

)

and X = [X

|. ..|X

y: Number of clusters in the repair shop.

Problem parameters:

N: Number of distinct type of repairables (SKUs).

Failure rate of SKU type i ( i = 1, . .., N).

: Service rate of SKU type i ( i = 1,.. .,N).

: Inventory holding cost of SKU type i per unit

time per part ( i = 1,. . .,N).

b: Penalty cost for each back ordered demand per

unit time, which is equivalent to paying per unit

time per technical system that is down because

of a lack of spare parts.

f : Operation cost of a server per unit time (e.g.,

annual wage).

: Cost of having skills to repair SKU type i per

unit time per server (i = 1, ..., N) (e.g., annual

qualiﬁcation bonus).

ε: Very small positive real number.

The objective function in Eq.(1) has four cost

terms namely server (capacity), cross-training, hold-

ing and backorder costs. Objective function considers

several trade-offs between the cost terms such as the

cost of holding excess inventory and the cost of down-

time, and also the trade-off between the cost of hav-

ing single or several clusters that include dedicated or

cross-trained servers.

min

S, X, Z

∑

k=1

f z

∑

k=1

∑

i=1

∑

i=1

+ b

∑

i=1

EBO

,X, Z] (1)

The penalty (backorder) cost term is calculated using

the penalty cost b and the expected total number of

backordered parts EBO

,X, Z] for each SKU type

A Pooling Strategy for Flexible Repair Shop Designs

273

2 3

4 5

Failed Parts

Installed Base

Spare Part

Inventories

Repair Shop

Random Failures of Parts

(a) Pooled Design with Two Clusters

2 3

4 5

Failed Parts

Random Failures of Parts

(b) ‘N’ and ‘W’ Designs inside Two Clusters

Figure 1: A comparative example for single echelon spare part supply systems with different (pooled vs. not pooled) repair

shop designs.

i in the steady-state; under the given initial inventory

level S

, pooling scheme of the repair shop X and the

server assignment policy Z. The variable X represents

the (N × y) matrix of the binary decision variables

denoting how SKUs are pooled in the repair shop,

and the variable Z represents a (1 × y) row matrix of

integer decision variables z

denoting the number of

servers in the each cluster of the repair shop.

Constraints (2) and (4) ensure that pooling scheme

X satisﬁes mutually exclusive and total exhaustive

condition for each cluster, i.e., any SKU type being

repaired by exactly one cluster. Queues (number of

waiting failed spares) in each cluster have to be in ﬁ-

nite queue length at steady-state to prevent overload-

ing of repair shop. Thus, the stability of system is

guaranteed by constraint (3) and (5) by assigning suf-

ﬁcient number of servers to each cluster. Constraints

between Eqs.(4)-(7) are required for non-negativity

and integrality of the variables.

∑

k=1

= 1 i = 1, ..., N (2)

∑

i=1

≤ z

− ε k = 1,.. . ,y (3)

∈ {0,1} i = 1, ..., N k = 1,.. .,y (4)

∈ Z

k = 1,.. . ,y (5)

∈ N

i = 1, ..., N (6)

y ∈ {1, ..., N} (7)

For not an overloaded system, the overall utilization

rate of a particular cluster k (

∑

i=1

/µ

) must be

strictly smaller than the capacity (total number of

servers in the cluster z

) of that cluster, which is en-

sured by the parameter, ε.

3 SOLUTION ALGORITHM

The optimal values of decision variables are searched

sequentially by ﬁxing the values of some decision

variables and optimizing the remaining ones. First,

feasible partitions of SKUs, i.e., pooling policies X

are generated. Afterwards, capacity levels Z and

basestock inventory levels S are optimized under the

given pooling scheme for each cluster. The visual

ﬂow of the proposed solution heuristic together with

its sub-routines and their interactions with each other

are depicted in Figure 2.

To ﬁnd partitions of SKUs into clusters, all SKUs

are sorted in ascending order by their service rates µ

so that SKUs closer in service rates are likely to be in

the same cluster. This is aimed for decreasing vari-

ations in the service times of SKUs in clusters. De-

crease in the variation of service times usually leads

to decrease in number of failed parts waiting for repair

in the cluster and eventually lowering the number of

backorders and the total cost.

In the next step, sorted list of SKUs is divided into

smaller lists that have a size of n

max

or less. The trade-

off between the run time of algorithm and the output

solution quality has to be taken into account when de-

termining the value of n

max

. We set n

max

as 10 for our

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

274

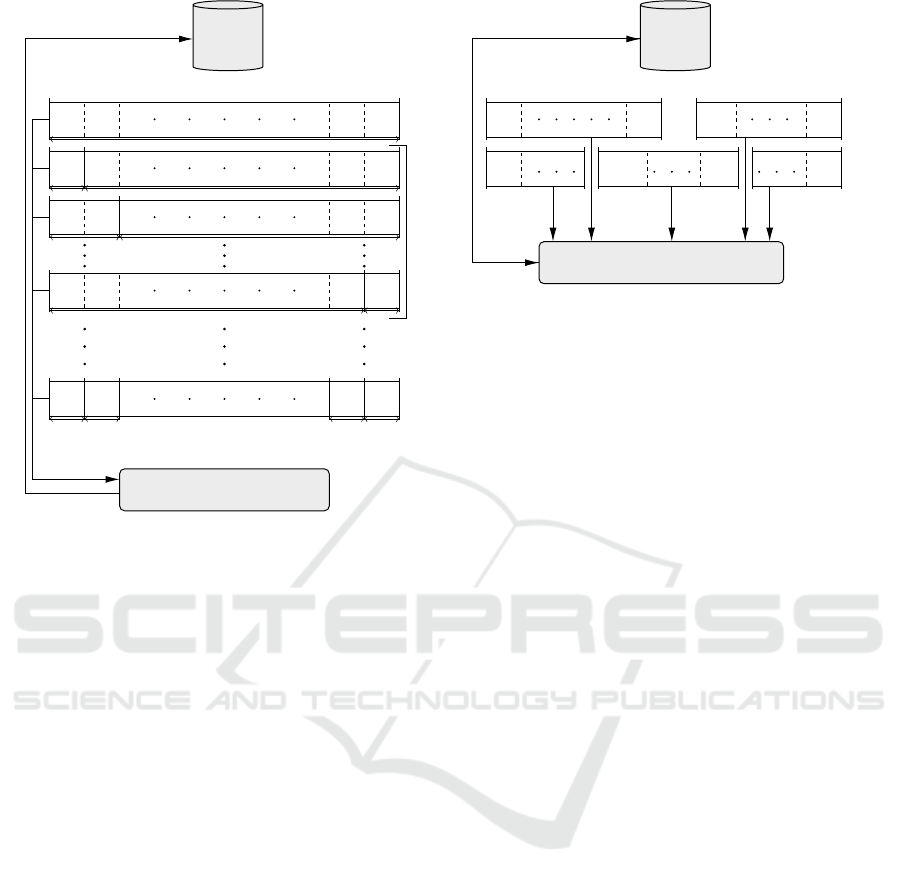
y := 1

N −1

cluster 1

N −1

cluster 1 cluster 2

N −1

cluster 1 cluster 2

N −1

cluster 1 cluster 2

y := N

N −1

cluster 1 cluster 2 cluster N-1 cluster N

y := 2

Capacity & Inventory Level

Optimization Modules

Solution

Database

Values of (X, Z, S)

Optimized Costs

Pooling Policy

(X)

Sorted SKU index set

(a) Pooling policy generation and optimization by

BruteForce() function for N ≤ n

max

−l+1

max

BruteForce() Function

Solution

Database

Recording optimal

solution

Retrieving

optimal

solution

Sub-Problem 1 Sub-Problem 2

(b) Calling BruteForce() function and generating Sub-Problems

for N > n

max

Figure 2: The proposed sequential solution heuristic.

experimental runs. For the smaller list (N ≤ n

max

BruteForce() function is invoked as depicted in Fig-

ure 2(a). BruteForce() takes an array of SKU in-

dexes as an input and slices it into sub-arrays for given

number of clusters y from 1 to the length of the in-

put array. Each slice/sub-array corresponds to a clus-

ter in a pooled repair shop, and each slicing scheme

corresponds to a particular pooling policy X. For the

larger sorted SKU index sets, it is not possible to enu-

merate all slicing schemes with BruteForce() func-

tion. Thus, we divide the problem into sub-problems

that have the maximum size of n

max

or less as in Fig-

ure 2(b) and call BruteForce() for each sub-problem

obtained after division. Then, we generate new sub-

problems by combining the last and the ﬁrst elements

of adjacent sub-problems. At each iteration, we insert

a new SKU index to newly generated sub-problem till

the size of the problem reaches n

max

After the generation of the pooling policy X via

above described heuristic, capacity and inventory

level optimization modules are called. These modules

rely on the fact that for every feasible policy X, each

cluster can be analyzed and optimized separately due

to the clusters being mutually exclusive and indepen-

dent from each other. The decomposition of the re-

pair shop in sub-systems by pooling reduces the com-

plexity of the problem and enables the use of queue-

theoretical approximations to optimize the inventory

and capacity levels. In this direction, each cluster k in

the repair shop for given number of servers can be an-

alyzed as a multi-class multi-server M/M/z

queuing

system.

The probability distribution of the number of

failed SKU type i at the steady-state, p

(q), is re-

quired to evaluate EBO

,Z, X]. To calculate the

probability distribution of the number of failed SKU

type i, the approach proposed by Van Harten and

Sleptchenko (2003) is used. Nonetheless, computa-

tional burden arises when number of SKU types and

number of servers increases in the cluster. To over-

come this issue, queuing approximation discussed in

Altiok (1985) and Van Der Heijden et al. (2004) is

used. In this approximation, marginal probability dis-

tribution (and several performance characteristics) of

the SKU type i in the cluster k is derived by aggregat-

ing all other SKUs in the cluster k into a single SKU

type (class). To obtain the remaining distributions for

the other SKUs in the cluster, the procedure is re-

peated. Basically, a multi-class multi-server queuing

system including two-class (two SKUs) is solved for

each SKU in the cluster rather than solving one multi-

class multi-server with larger number (total number of

SKUs in the cluster) of SKUs.

By using the approximated distributions, ˜p

(q),

A Pooling Strategy for Flexible Repair Shop Designs

275

the sum of holding and backorder costs h

bEBO

,Z, X] can be minimized by the smallest S

for which Eq.(8) holds.

∑

q=0

˜p

(q) ≥

b − h

i = 1, ..., N (8)

A detailed discussion of capacity and inventory level

optimization modules can be found in Turan et al.

(2017).

4 NUMERICAL STUDY

A full factorial design of experiment (DoE) with 7

factors and 2 levels per factor is used to generate the

testbed with total of 128 test instances (Sleptchenko

et al., 2016). The number of SKUs, N, and the initial

total number of servers, M, are the ﬁrst two DoE fac-

tors with levels 10 and 20 for the numbers of SKUs,

and 5 and 10 for the initial numbers of servers. The

failure rates and the service rates are generated based

on the system (repair shop) utilization rate with the as-

sumption that all SKUs are processed on all servers,

i.e., a repair shop design with one cluster and fully

ﬂexible servers. The system utilization rate, ρ, is the

third design factor with levels 0.65 and 0.80. For the

chosen utilization rate, we randomly generate two sets

of parameters:

(a) the failure rates λ

, such that

∑

i=1

= 1, and

(b) workload percentages δ

, such that

∑

i=1

= 1.

Using the generated λ

and δ

, we produce the service

rates µ

as µ

ρM

, where δ

ρM is the total workload

of SKU type i. The pattern of the holding costs, h

is the fourth design factor with two variants (levels):

(i) IND: completely randomly (independent) within

a range [h

min

max

], and (ii) HPB: hyperbolically re-

lated to the workloads w

= λ

/µ

= δ

ρM:

max

− h

min

+ 10

−w

min

max

−w

min

+ 1

− 10 + h

min

+ ξ

where

∈ U[−

max

− h

min

max

− h

min

= min

i=1,...,N

and w

max

= max

i=1,...,N

The parameters of the hyperbolic relation are cho-

sen such that it replicates some of the real-life sce-

narios where more expensive repairables are repaired

less frequently. The minimum holding cost, h

min

, is

the ﬁfth factor with levels 1 and 100. The maximum

holding cost is ﬁxed at 1,000. The server cost, f , and

the skill cost, c

, are the last two factors in our DoE.

The server cost levels are set as 10,000 and 100,000

(10h

max

and 100h

max

). The skill cost is assumed as

1% or 10% of the chosen server cost for all SKUs.

The penalty cost, b, is set as ﬁfty-fold of the aver-

age holding cost so that about 98% of requests can be

met from spare stocks. That means the probability of

backorder is only 0.02. The overview of all factors

and levels are presented in Table 1.

Table 1: Problem parameter variants for test bed.

Factors Levels

No. of SKUs (N) [

10, 20

]

No. of Initial servers (M) [

5, 10

]

Utilization Rate (ρ) [

0.65, 0.80

]

Minimum Holding Cost (h

min

) [

1, 100

]

Maximum Holding Cost (h

max

) 1000

Holding cost/Workload relation [

IND, HPB

]

Server Cost ( f ) [

10h

max

, 100h

max

]

Cross-Training Cost (c

) [

0.01 f , 0.10 f

]

Penalty Cost (b) 50

∑

i=1

∑

i=1

The total system costs found by the proposed

pooling heuristic are compared with the costs ob-

tained from fully ﬂexible (a single cluster where any

SKU can be processed on any server) and dedicated

(where number of clusters equal to number of SKUs)

designs. Table 2 summarizes cost reductions for dif-

ferent problem factors. On an average, the heuristic

that produce only pooled designs can produce ∼45%

and ∼25% savings in comparison with dedicated and

fully ﬂexible designs, respectively. In some extreme

settings, average cost reductions reach to 55% and

43% compared with dedicated and fully ﬂexible sys-

tems, respectively.

Table 2: Average cost reductions by pooling under different

factors.

Factor Levels Dedicated Fully Flexible

Number of SKUs (N)

10 35.19% 22.00%

20 55.65% 28.11%

Number of Initial Servers (M)

5 53.76% 23.43%

10 37.08% 26.68%

Utilization Rate (ρ)

0.65 48.01% 24.30%

0.80 42.83% 25.81%

Minimum Holding Cost (h

min

)

1 45.84% 24.81%

100 45.00% 25.30%

Holding Cost/Work Load Relation

IND 44.42% 24.04%

HPB 46.42% 26.08%

Server Cost ( f )

10h

max

39.95% 22.44%

100h

max

50.89% 27.67%

Cross-Training Cost (c

)

0.01 f 50.22% 9.93%

0.1 f 40.62% 40.18%

Average 45.42% 25.06%

The analysis also shows that when the cost of hav-

ing an extra skill is relatively small compared to that

for having an extra server (i.e., the case of cross-

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

276

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8

·10

Pooling Heuristic

Run Time (CPU seconds)

Figure 3: Run time performance of pooling heuristic.

training cost being equivalent 0.01 f ), fully ﬂexible

design is as good as a pooled system. On the other

hand, dedicated and fully ﬂexible systems perform

similarly where there is a high cost of cross-training.

Table 3 shows the average number of servers used,

skills assigned to a server and the percentage of cross-

training per server under different factors and solution

algorithms. The percentage of cross-training is ob-

tained from a ratio of the number of skills allocated

into a server to the total number distinct SKUs, N, in

the system. The dominate factor affecting the num-

ber of servers used is the number of initial servers, M.

This factor sets an average value of the required num-

ber of operational servers to achieve a predetermined

overall utilization rate for the whole system. Thus, we

observe a nearly doubled increase from 5.03 to 9.17

in the average number of operational servers when the

number of initial servers increases from 5 to 10.

Table 3: Capacity and cross-training analysis under differ-

ent factors.

# server # skill %cross

Factor Levels used per server training

Number of SKUs (N)

10 7.03 3.81 38.16

20 7.17 5.58 27.93

Number of Initial Servers (M)

5 5.03 5.24 37.20

10 9.17 4.16 28.89

Utilization Rate (ρ)

0.65 6.51 4.67 32.64

0.80 7.68 4.73 33.45

Minimum Holding Cost (h

min

)

1 7.06 4.69 33.09

100 7.14 4.70 33.00

Holding Cost/Work Load Relation

IND 7.23 4.88 34.17

HPB 6.96 4.51 31.92

Server Cost ( f )

10h

max

7.65 5.06 35.48

100h

max

6.54 4.34 30.61

Cross-Training Cost (c

)

0.01 f 6.93 6.06 42.66

0.1 f 7.26 3.33 23.43

Average 7.10 4.70 33.05

At the optimal design, %cross-training per server

ﬂuctuates between 30%-40%, which shows that par-

tial ﬂexibility; i.e., partial cross-training is usually

sufﬁcient for optimal system performance.

All the experiments are implemented on a com-

puter with 16 GB RAM and 2.8 GHz i7 CPU. Fig-

ure 3 shows a boxplot of run time performances for

all cases. The presented heuristic converges quite

fast in most of the cases and provides the ﬁnal solu-

tion within 5000 cpu seconds with a median run time

of 2000 seconds, which is still acceptable for tacti-

cal/operational levels decisions in real-life spare part

supply systems.

5 CONCLUSIONS

When designing a spare part supply network for re-

pairable parts that balances cost efﬁciency with ef-

fectiveness, several questions in both strategic and

tactical nature have to be answered. In this article,

the joint problem of resource pooling, inventory al-

location and capacity level designation of the repair

shop is analyzed and a solution heuristic is devel-

oped. Performed extensive numerical experiments

conclude that the pooled designs result in cost savings

of around 45% and 25% in comparison to dedicated

and fully ﬂexible designs, respectively. Besides, we

observe that the optimal repair shop designs can be

achieved by partially cross-training servers.

As further research possibilities, designing new

clustering heuristics or meta-heuristics that will gen-

erate better pooling schemes with less computational

complexity would be invaluable contribution. It

would be also worthwhile to investigate effects of pri-

ority rules by taking into account service rates and

costs characteristics of the SKUs.

ACKNOWLEDGEMENT

This publication was made possible by the NPRP

award [NPRP 7-308-2-128] from the Qatar National

Research Fund (a member of The Qatar Foundation).

The statements made herein are solely the responsi-

bility of the author[s].

REFERENCES

Altiok, T. (1985). On the phase-type approximations of gen-

eral distributions. IIE Transactions, 17(2):110–116.

Diaz, A. and Fu, M. C. (1997). Models for multi-echelon

repairable item inventory systems with limited repair

A Pooling Strategy for Flexible Repair Shop Designs

277

capacity. European Journal of Operational Research,

97(3):480–492.

Duffuaa, S. O. (2000). Mathematical models in main-

tenance planning and scheduling. In Maintenance,

Modeling and Optimization, pages 39–53. Springer.

Keizer, M. C. O., Teunter, R. H., and Veldman, J. (2016).

Clustering condition-based maintenance for systems

with redundancy and economic dependencies. Euro-

pean Journal of Operational Research, 251(2):531–

540.

opez-Santana, E., Akhavan-Tabatabaei, R., Dieulle, L.,

Labadie, N., and Medaglia, A. L. (2016). On the com-

bined maintenance and routing optimization problem.

Reliability Engineering & System Safety, 145:199–

214.

Qin, R., Nembhard, D. A., and Barnes II, W. L. (2015).

Workforce ﬂexibility in operations management. Sur-

veys in Operations Research and Management Sci-

ence, 20(1):19–33.

Rappold, J. A. and Van Roo, B. D. (2009). Designing multi-

echelon service parts networks with ﬁnite repair ca-

pacity. European Journal of Operational Research,

199(3):781–792.

Sherbrooke, C. C. (1968). Metric: A multi-echelon tech-

nique for recoverable item control. Operations Re-

search, 16(1):122–141.

Sleptchenko, A., Turan, H. H., Pokharel, S., and

ElMekkawy, T. Y. (2016). Cross training policies for

repair shops with spare part inventories. submitted for

publication.

Sleptchenko, A., Van der Heijden, M., and Van Harten, A.

(2003). Trade-off between inventory and repair capac-

ity in spare part networks. Journal of the Operational

Research Society, 54(3):263–272.

Srivathsan, S. and Viswanathan, S. (2017). A queueing-

based optimization model for planning inventory of

repaired components in a service center. Computers

& Industrial Engineering, 106:373–385.

Tekin, E., Hopp, W. J., and Van Oyen, M. P. (2009). Pool-

ing strategies for call center agent cross-training. IIE

Transactions, 41(6):546–561.

Turan, H. H., Sleptchenko, A., Pokharel, S., and

ElMekkawy, T. Y. (2017). A clustering-based repair

shop design for repairable spare part supply systems.

submitted for publication.

Van Der Heijden, M., Van Harten, A., and Sleptchenko,

A. (2004). Approximations for markovian multi-class

queues with preemptive priorities. Operations Re-

search Letters, 32(3):273–282.

Van Harten, A. and Sleptchenko, A. (2003). On markovian

multi-class, multi-server queueing. Queueing systems,

43(4):307–328.

ICORES 2018 - 7th International Conference on Operations Research and Enterprise Systems

278