Optimization of Garbage Hauling Route in Medan Kota District

using Saving Matrix Method to Minimize Cost

Khalida Syahputri

, Rahmi M. Sari

, Mangara M. Tambunan

, Indah Rizkya

, Ikhsan Siregar

and

Josua P. Simanjuntak

Industrial Engineering, Faculty of Engineering, Universitas Sumatea Utara, Jl. Almamater, Padang Bulan, Medan,

Indonesia

Keywords: Garbage Hauling Route.

Abstract: Medan Kota district is one of the district with the highest population density in the city. This has resulted in

the high rate of garbage heap in the Medan Kota that must be managed. Limitations of the means of

transporting garbage resulted in the accumulation of garbage in various TPS in Medan district. The purpose

of this research, applying Saving Matrix method to optimize the route of transporting garbage in the city field.

This method enables route optimization with respect to vehicle capacity and garbage volume for each TPS.

The data used is the distance between Pool with the point of point of TPS and the distance between the points

of TPS, the amount of garbage volume of each TPS point, and the capacity of the vehicle. The route

optimization using Saving Algorithm will result in a route that minimizes the cost of fuel by the amount of

garbage transported more. The route generated by using the Savings Algorithm to successfully save the

distance as far as 95 Km and save the cost of Rp. 59.525.416 / year.

1 INTRODUCTION

Rate of garbage heap in developing countries will

always be high. This was influenced by high levels of

population, industrialization, urbanization, and

economic growth.

Economic garbage management

consists of garbage reduction and garbage handling

efforts. garbage reduction efforts consist of limiting

garbage heap, recycling waste, and reuse of waste.

garbage management efforts include sorting,

collection, transporting, processing, and final

processing (Bozkurt, 2015).

Medan Kota district is

one of the biggest sub-district in Medan with the

population of 118.405 people and is categorized as

solid city based on SNI 19. In Medan Kota sub-

district, there are shopping area, trade, market that is

Sambu Market Center, sports facility that is Teladan

Stadium (C. Bozkurt, 2015).

The Increasing number of residents in Medan

Kota district, will also increase the amount of garbage

volume in Medan city. Based on the results of recap

at department of public works and housing (DPUP)

municipalities, the volume of garbage in Medan Kota

district from year to year also increased. So it is

necessary to do proper garbage management. The

process of transporting garbage is done by way of

garbage transportation from garbage bins that were

spread in every public road. Because of the limited

number of transport vehicles, then the process of

transporting garbage can only be executed as much as

one time round in one day from the base to every

particular service area and then taken to the landfill

and ended up in the base and not optimal journey

truck transport truck that resulted in garbage

accumulation in some regions (Kinobe, 2016).

There were many factors that could influence in

the process of transporting garbage from the starting

point, in this case DPUP to the end point of the

landfill, including the capacity of transport means, the

volume of garbage in each TPS and the distance

travelled in the transport process. The garbage

transport process should each pay attention to the

capacity of each vehicle and the demand capacity

(waste) on each route the issue of garbage distribution

involves several major considerations including

vehicle routes, vehicles to minimize distribution

costs, so as to expand the service area from garbage

collection with limited fleets).

The problem of distribution routes was a very

much discussed problem in terms of optimization

such as about traveling salesman problems and

vehicle routing problems and for that has been done a

lot of research to discuss the problem VRP in order to

Syahputri, K., Sari, R., Tambunan, M., Rizkya, I., Siregar, I. and Simanjuntak, J.

Optimization of Garbage Hauling Route in Medan Kota District using Saving Matrix Method to Minimize Cost.

DOI: 10.5220/0010077702170221

In Proceedings of the International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches (ICOSTEERR 2018) - Research in Industry 4.0, pages

217-221

ISBN: 978-989-758-449-7

 2020 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved

217

obtain the optimal technique to solve the problem

(Hannan, 2018). Traveling salesman problems and

routing issues vehicles are a very complex problem in

the field of logistics distribution because they should

involve a minimum cost design, determining the

delivery route from start to finish and determining the

start of the depot and the end of the depot

(Armenzani, 2017). The solutions generated on the

VRP problem are increased exponentially and to find

the optimal solution in VRP problems can be solved

by using heuristic methods that the proposed heuristic

approach allows us to deal with problems in a short

time using the heuristic method (Heechul, 2016).

Clarke and Wright create a heuristic algorithm to

complete the VRP based on the concept of austerity

which provide optimal solution and easy way to

calculate and easier to comprehend. The concept of

this savings was with the concept of cost that can be

obtained by combining the two routes to the top and

making it one. This was shown in the figure below

where 0 represents the depot and i, j as the customer

(Fathoni, 2017) of modified saving algorithms to

create feasible solutions for VRPP. The idea was to

first serve each customer with a special route, and

then combine the route pairs as long as the positive

savings can be realized and the vehicle's capacity was

not violated. In each iteration, we combine pairs with

the highest savings. To combine the two routes r1 and

r2, we only consider the edge incidence to the depot

and remove one side of r1 and one side r2. Then, we

replace it with an edge directly connecting the

appropriate customer i from r1 and j r2 (Babaee,

2018). The Saving Matrix method was the method

used to determine the route of product distribution to

the marketing area by determining the distribution

route to be traveled and the number of vehicles

routing based on the capacity in order to obtain the

shortest route and minimal transportation cost. The

Saving Matrix method was also one of the techniques

used to schedule a limited number of vehicles from

facilities with a different maximum capacity. The

austerity matrix shows the savings that occur when

combining two possible TPS into one truck so that it

can save the distance, time, and transportation costs

(Babaee, 2018).

2 METHODOLOGY

This research was conducted in the district of Medan

Kota. The object studied was the route of transporting

garbage from the pool to the TPS and from the TPS

to the landfill located in Marelan Raya Street, Market

V TPA Plunge, Rengas Island, Medan Marelan. The

data collected to conduct the research is the data of

the number of temporary garbage disposal sites, the

number of consumer demand or the volume of

landfills.from the data obtained will be processed

using Clarke and Wright Saving Matrix method, the

route of garbage transportation in sub-district of city

was divided into 4 polls where each poll has different

number of different TPS for each POOL

The first step done in this research was to create a

matrix that contains distance between TPS the

distance between each pair of locations to visit.

Determining the distance was based on the distance

of each TPS where the location of each TPS can be

symbolized as notation, Juanda street was symbolized

by A1, Sisingamangaraja street symbolized by A2,

Mahkamah street symbolized by A3, Tengah street

symbolized by A4, Samarinda symbolized with

Rahmadsyah by A6 , Raja street symbolized by B1,

Pelangi steet symbolized by B2, Turi street

symbolized by B3, Gedung Arca street symbolized by

B4, Halat street symbolized by B5, Halat street

symbolized by B6, Juanda street symbolized by B7,

H M Joni street symbolized by B8, Seksama street

symbolized by C1, Saudara street symbolized by C2,

Bahagia street symbolized by C3, Kemiri 1 street

symbolized by C4, Kemiri 2 street symbolized by C5,

Pelajar street symbolized by D1, Jati street

symbolized by D2, Aman street symbolized by D3,

Meranti street symbolized D4. Sakti Lubis street

symbolized by D5, Pintu Air street symbolized by

D6, Busi street symbolized by D7, Gg Pegawas

symbolized by D8, Bali street symbolized by D9,

Sempurna symbolized by E1, Santun street

symbolized by E2, Laksana street symbolized by E3,

Amalium street symbolized by I4, and Rahmadsyah

street symbolized by E5. The second stage is to create

a distance-saving Matrix that shows the savings that

occur when combining two possible TPS into one

truck so that it can save the distance, time, and

transportation costs.

S (x, y) = Dist (Center, x) + Dist (Center,

) - Dist (x,

)

(1)

Third stage. Allocate TPS points to a transport

route. The first step of each TPS was allocated to

different trucks or routes. The second step was to

combine two routes based on the saving distance

obtained using the largest Saving Matrix formula and

check whether the merger was feasible or not. It was

said to be appropriate if the total shipments that

should be passed through the route do not exceed the

capacity of the conveyance. The integration of the

route was focused on saving the greatest distance to

ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches

218

obtain the distance efficiency, so the time spent will

be faster.

The fourth stage. This stage aims to minimize the

travel distance that must be transported each means

of conveyance. To get an optimal transportation

route, can be done two stages of determining the

initial delivery route for each vehicle and make

improvements to the route that is not feasible. The

fifth stage. Calculates the fuel cost of each total

distance with the fuel consumption for each garbage

truck average of 3km / liter and the diesel price is Rp

5,150.

3 RESULTS AND DISCUSSION

3.1 Truck Transportation Garbage

Route in Medan Kota District

In this research, the data consists of Primary Data and

Secondary Data. Primary data collected were among

others: truck route of garbage transport during

operational time and location of service area; truck

capacity; and the amount of garbage heap in each

service area. Secondary data collected were: number

and type of garbage truck, truck data (type, police

number, and year of output); data speed of truck

(speed), time of loading and unloading of waste,

garbage transport vehicle in sub district Medan of 7

unit consisting of:

1. In pool A there was 1 unit of truck garbage of

capacity 8m

2. In pool B there were 2 units of 8m

capacity truck.

3. In pool C there was 1 unit of 8m

capacity truck.

4. In pool D there were 2 units of 8m

capacity truck.

5. In pool E there was 1 unit of 8m

capacity truck.

Research determination of garbage dumping route

in sub-district of Medan Kota with the capacity of

garbage

truck

which the actual route from

garbage collection in sub-district of Medan Kota.

On the actual route the garbage truck that was in

each pool only runs every TPS once a day and when

the volume of garbage meet the capacity of the truck,

not yet lifted will resume on the next day, on Monday

the truck in pool E will lift the garbage at A1-A2-A3

point with a volume of 7.5 after lifting the truck truck

will depart to TPA, and for the garbage located at A5-

A4-A6 will be taken the next day because each truck

there was only one ritation per day. After using

Clarke method and Wright Saving Matrix could be

obtained new route which can be seen in Table 2.

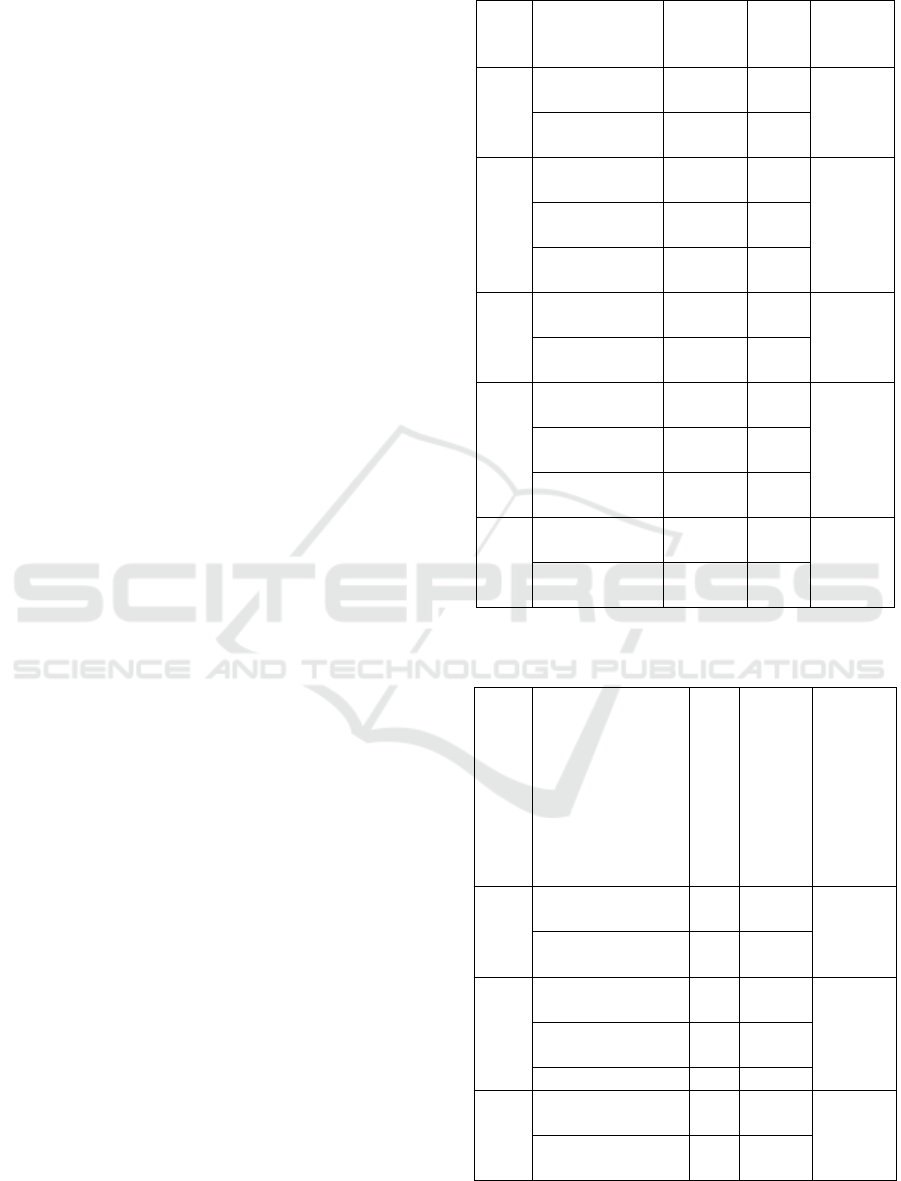
Tabel 1: Actual Route

Pool Route

Volume

Transpo

rted (m

Dista

nce

(km)

Cost

Pool

A0-A1-A2-

A3-X-A0

7,5

46,60

Rp468.

135

A0-A5-A4-

A6-X-A0

7,5

44,3

Pool

B0-B4-B7-B3-

X-B0 7

62,3

Rp829.

923

B0-B6-B1-B8-

X-B0 8

50,75

B0-B5-B2-X-

B0 5,5

48,1

Pool

C0-C1-C4-C2-

X-C0 7

53,90

Rp545.

128

C0-C3-C5-X-

C0 6,

51,95

Pool

D0-D6-D2-

D7-X-D0 7,5

53,9

Rp841.

510

D0-D3-D5-

D1-X-D0 8

56,9

D0-D9-D4-

D8-X-D0 7

52,6

Pool

E0-E4-E2-E1-

X-E0

7,5

58,70

Rp628.

815

E0-E4-E3-X-

4,5

63,40

Tabel 2: Actual Route

Pool Route

Vol

Tra

nsp

orte

)

Distan

(km)

Cost

Pool

A0-A4-A1-A3-X-

42,40

Rp418.

438

A0-A2-A6-A5-X-

38,85

Pool

B0-B4-B6-B7-X-

B0 8 43,75

Rp695.

250

B0-B2-B3-B8-X-

B0 7,5 43,75

B0-B1-B5-X-B0 6 47,50

Pool

B0-C5-C1-C2-X-

C0 6,5 49,00

Rp489.

250

C0-C4-C3-X-C0 6,5 46,00

Optimization of Garbage Hauling Route in Medan Kota District using Saving Matrix Method to Minimize Cost

219

Pool

D0-D8-D7-D6-X-

D0 8 53,15

Rp831.

210

D0-D1-D9-D3-X-

D0 8 57,70

D0-D4-D5-D2-X-

D0 6,5 50,55

Pool

E0-E3-E5-E4-X-

51,70

Rp587.

100

E0-E1-E2-X-E0 5,5

62,30

From the Table 1. Can be seen that there were 5

garbage truck pools that serve garbage collection in

each TPS in the Medan Kota district, the results

obtained were the garbage in the coverage TPS of

pools E, F, G, H and I can be trapped in one day 2

garbage hauling and in pools F and H there were 3

routes that must be trucked by garbage trucks but in

pools F and H each have 2 different trucks with other

pools that have only one truck, the determination of

the route of garbage by using Saving Matrix method

was based on the volume and capacity of garbage

truckers. On the trucking trip, each truck will do two

ritations a day if the truck was only one ritual in one

day, the garbage in each TPS is all due to the limited

number of trucks and the limited capacity of the

conveyance at each pool.

3.2 Comparison of the Total Actual

Cost with the Cost of the Proposed

Route

Based on the determination of the cost of truck

transporting garbage using saving matrix method,

then compare between actual route and with the

regular route.

Table 3: Comparison Of Total Actual Cost With Cost Of

Proposed Route

No Pool

Total Distance (km)

Actual Proposal

1 E Rp468.135 Rp418.438

2 F Rp829.923 Rp695.250

3 G Rp545.128 Rp489.250

4 H Rp841,510 Rp831.210

5 I Rp628.815 Rp587.100

From the table it can be seen that the total fuel cost

of the actual route is greater than the total cost of the

proposed route with savings of 8.8%. Peter

Majercak's research on the determination of the

distribution route of goods to each consumer by

considering the capacity of the truck using the Clark

and Wright's Savings Algorithm method successfully

minimizes the delivery distance of the product to the

consumer. Clark and Wright's Savings Algorithm

methods have also managed to minimize waste

transport distance between TPS in Medan Kota

District.

4 CONCLUSIONS

The total traveled distance by all trucks so far in

Medan Town sub-district is 643.4 km. After using the

saving matrix method the total traveled distance

become 586.65 km km. The total fuel cost incurred

by the urban district is Rp. 3.313.000,- per month.

After using the saving matrix method the total cost of

board materials issued to RP. 3.021.000,- per month.

The percentage of total cost savings is 8.8%, The

results shows that the route and cost of fuel with

saving matrix method is minimized.

ACKNOWLEDGEMENTS

This work has been fully supported by TALENTA

Research Program (Universitas Sumatera Utara),

No:2590/UN5.1.R/PPM/2018, March 16th, 2018

REFERENCES

Cuma Bozkurt, 2015. International Journal Of Energy

Economics And Policy Vol 5, No 2.

Cuma Bozkurt.” Industrial-waste management in

developing countries: The case of Lebanon Volume 61,

Issue 4, April 2015.

Kinobe,j.r dkk, 2016. Habitat International Volume 49,

October 2015, Pages 126-137

M.A.Hannan, M.A 2018. Waste Management Volume 71,

January 2018. Pages 31-41

Gendreau Michel.” Efficiently Solving Very Large Scale

Routing Problems4 Florian Arnold1”, diakses dari

https://www.researchgate.net/profile/Florian_Arnold/p

ublication/322317599

Armenzoni 2017. Distribution Journal of Advanced

Transportation Volume 2017.

Heechul Bae 2016, Mathematical Modelling 40(13-14)

Fathoni, Ali, 2017. International Journal of New

Technology and Research Volume-3, Issue-10

Babaee dkk 2018 , Sustainability 2018. 10(5), 1366

Fisher, M.L. 1995. “Vehicle Routing in Operations

Research and Management Science”Vol.8.

Amsterdam, New York, Elsevier

ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramiﬁcation Researches

220

Majercak,Peter. 2016. Application of Clark and Wright´s

Savings Algorithm Model to Solve Routing Problem in

Supply Logistics Vol 25 (2), PP.125-145

Uchoa, E., Pecin, D., Pessoa, A., Poggi, M., Vidal, T., and

Subramanian, A. 2017. European Journal of

Operational Research, 257(3):845-858.

Optimization of Garbage Hauling Route in Medan Kota District using Saving Matrix Method to Minimize Cost

221