Numl: A Strongly Typed Language
for Numerical Accuracy
†
Matthieu Martel
Laboratoire de Math
´
ematiques et Physique (LAMPS),
Universit
´
e de Perpignan Via Domitia, France
Abstract. It is well-known that numerical computations may sometimes lead to
wrong results because of roundoff errors. We propose an ML-like type system
(strong, implicit, polymorphic) for numerical computations in finite precision,
in which the type of an expression carries information on its accuracy. We use
dependent types and a type inference which, from the user point of view, acts
like ML type inference. Basically, our type system accepts expressions for which
it may ensure a certain accuracy on the result of the evaluation and it rejects
expressions for which a minimal accuracy on the result of the evaluation cannot
be inferred. The soundness of the type system is ensured by a subject reduction
theorem and we show that our type system is able to type implementations of
usual simple numerical algorithms.
1 Introduction
It is well-known that numerical computations may sometimes lead to wrong results
because of the accumulation of roundoff errors [10]. Recently, much work has been
done to detect these accuracy errors in finite precision computations [1], by static [8,
11, 24] or dynamic [9] analysis, to find the least data formats needed to ensure a certain
accuracy (precision tuning) [14, 16, 23] and to optimize the accuracy by program trans-
formation [7, 20]. All these techniques are used late in the software development cycle,
once the programs are entirely written.
In this article, we aim at exploring a different direction. We aim at detecting and
correcting numerical accuracy errors at software development time, i.e. during the pro-
gramming phase. From a software engineering point of view, the advantages of our
approach are many since it is well-known that late bug detection is time and money
consuming. We also aim at using intensively used techniques recognized for their abil-
ity to discard run-time errors. This choice is motivated by efficiency reasons as well as
for end-user adoption reasons.
We propose an ML-like type system (strong, implicit, polymorphic [21]) for numer-
ical computations in which the type of an arithmetic expression carries information on
†
This work is supported by the Office for Naval Research Global under Grant NICOP
N62909-18-1-2068 (Tycoon project). https://www.onr.navy.mil/en/Science-Technology/ONR-
Global
Martel, M.
Numl - A Strongly Typed Language for Numerical Accuracy.
DOI: 10.5220/0008862701770200
In OPPORTUNITIES AND CHALLENGES for European Projects (EPS Portugal 2017/2018 2017), pages 177-200
ISBN: 978-989-758-361-2
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
177

its accuracy. We use dependent types [22] and a type inference which, from the user
point of view, acts like ML [17] type inference [21] even if it slightly differs in its im-
plementation. While type systems have been widely used to prevent a large variety of
software bugs, to our knowledge, no type system has been targeted to address numeri-
cal accuracy issues in finite precision computations. Basically, our type system accepts
expressions for which it may ensure a certain accuracy on the result of the evaluation
and it rejects expressions for which a minimal accuracy on the result of the evaluation
cannot be inferred.
In our type system, unification necessitates to solve sets of constraints made of
propositional logic formulas and relations between affine expressions over integers (and
only integers). Indeed, these relations remain linear even if the term to be typed contains
non-linear computations. As a consequence, these constraints can be easily checked by
a SMT solver (we use Z3 in practice [18]).
Let us insist on the fact that we use a dependent type system. Consequently, the
type corresponding to a function of some argument x depends on the type of x itself.
The soundness of our type system relies on a subject reduction theorem introduced in
Section 4. Based on an instrumented operational semantics computing both the finite
precision and exact results of a numerical computation, this theorem shows that the error
on the result of the evaluation of some expression e is less than the error predicted by
the type of e. Obviously, as any non-trivial type system, our type system is not complete
and rejects certain programs that would not produce unbounded numerical errors. Our
type system has been implemented in a prototype language Numl and we show that, in
practice, our type system is expressive enough to type implementations of usual simple
numerical algorithms [2] such as the ones of Section 6. Let us also mention that our type
system represents a new application of dependent type theory motivated by applicative
needs. Indeed, dependent types arise naturally in our context since accuracy depends on
values.
This article is organized as follows. Section 2 introduces informally our type system
and shows how it is used in our implementation of a ML-like programming language,
Numl. The formal definition of the types and of the inference rules are given in Section
3. Section 3.1 introduces the type system itself while Section 3.2 introduces the types of
the primitives of the language. A soundness theorem is given in Section 4. The imple-
mentation of the type system is discussed in Section 5. Sections 5.1 and 6 present the
unification algorithm and Section 6 presents experimental results Section 7 discuss the
special case of the IEEE754 floating-point arithmetic [1]. Section 8 describes related
work and Section 9 concludes.
2 Programming with Types for Numerical Accuracy
In this section, we present informally how our type system works throughout a pro-
gramming sequence in our language, Numl. First of all, we use real numbers r{s, u, p}
where r is the value itself, and {s, u, p} the format of r. The format of a real number is
made of a sign s ∈ Sign and integers u, p ∈ Int such that u is the unit in the first place
of r, written ufp(r) and p the precision (i.e. the number of digits of the number). For
inputs, p is either explicitely specified by the user or set by default by the system. For
178
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
178

Format Name p e bits e
min
e
max
Binary16 Half precision 11 5 −14 +15
Binary32 Single precision 24 8 −126 +127
Binary64 Double precision 53 11 −1122 +1223
Binary128 Quadruple precision 113 15 −16382 +16383
Fig. 1. Basic binary IEEE754 formats.
outputs, p is inferred by the type system. We have Sign = {0, ⊕, , >} and sign(r) = 0
if r = 0, sign(r) = ⊕ if r > 0 and sign(r) =  if r < 0. The set Sign is equipped
with the partial order relation ≺⊆ Sign × Sign defined by 0 ≺ ⊕, 0 ≺ , ⊕ ≺ > and
 ≺ >. The ufp of a number x is
ufp(x) = min

i ∈ N : 2
i+1
> x

= blog
2
(x)c . (1)
The term p defines the precision of r. Let ε(r) be the absolute error on r, we assume
that ε(r) < 2
u−p+1
. The errors on the numerical constants arising in programs are
specified by the user or determined by default by the system. The errors on the computed
values can be inferred by propagation of the initial errors. Similarly to Equation (1), we
also define the unit in the last place (ulp) used later in this article. The ulp of a number
of precision p is defined by
ulp(x) = ufp(x) − p + 1 . (2)
For example, the type of 1.234 is real{+, 0, 53} since ufp(1.234) = 0 and since
we assume that, by default, the real numbers have the same precision as in the IEEE754
double precision floating-point format [1] (see Figure 1). Other formats may be spec-
ified by the programmer, as in the example below. Let us also mention that our type
system is independent of a given computer arithmetic. The interpreter only needs to
implement the formats given by the type system, using floating-point numbers, fixed-
point numbers [12], multiple precision numbers
1
, etc in order to ensure that the finite
precision operations are computed exactly. The special case of IEEE754 floating-point
arithmetic, which introduces additional errors due to the roundoff on results of opera-
tions can also be treated by modifying slightly the equations of Section 3.
> 1.234 ;; (
*
precision of 53 bits by default
*
)
- : real{+,0,53} = 1.234000000000000
> 1.234{4};; (
*
precision of 4 bits specified by the user
*
)
- : real{+,0,4} = 1.2
Notice that, in Numl, the type information is used by the pretty printer to display only
the correct digits of a number and a bound on the roundoff error.
Note that accuracy is not a property of a number but a number that states how closely
a particular finite-precision number matches some ideal true value. For example, using
the basis β = 10 for the sake of simplicity, the floating-point value 3.149 represents π
1
https://gmplib.org/
179
Numl - A Strongly Typed Language for Numerical Accuracy
179

with an accuracy of 3. It itself has a precision of 4. It represents the real number 3.14903
with an accuracy of 4. As in ML, our type system admits parameterized types [21].
> let f = fun x -> x + 1.0 ;;
val f : real{’a,’b,’c} -> real{<expr>,<expr>,<expr>} = <fun>
> verbose true ;;
- : unit = ()
> f ;;
- : real{’a,’b,’c} -> real{(SignPlus ’a ’b 1 0),((max ’b 0) +_ (sigma+ ’a 1)),
((((max ’b 0) +_ (sigma+ ’a 1)) -_ (max (’b -_ ’c) -53))-_ (iota (’b -_ ’c) -53))} = <fun>
In the example above, the type of f is a function of an argument whose parame-
terized type is real{’a, ’b, ’c}, where ’a, ’b and ’c are three type variables. The
return type of the function f is Real{e
0
,e
1
,e
2
} where e
0
, e
1
and e
2
are arithmetic
expressions containing the variables ’a, ’b and ’c. By default these expressions are
not displayed by the system (just like higher order values are not explicitly displayed
in ML implementations) but we may enforce the system to print them. In Numl, we
write +, -,
*
and / for the operators over real numbers. Integer expressions have type
int and we write + , - ,
*
and / for the elementary operators over integers. The
expressions arising in the type of f are explained in Section 3. As shown below, various
applications of f yield results of various types, depending on the type of the argument.
> f 1.234 ;;
- : real{+,1,53} = 2.234000000000000
> f 1.234{4} ;;
- : real{+,1,5} = 2.2
If the interpreter detects that the result of some computation has no significant digit,
then an error is raised. For example, it is well-known that in IEEE754 double precision
(10
16
+ 1) − 10
16
= 0. Our type system rejects this computation.
> (1.0e15 + 1.0) - 1.0e15 ;;
- : real{+,50,54} = 1.0
> (1.0e16 + 1.0) - 1.0e16 ;;
Error: The computed value has no significant digit. Its ufp is 0 but
the certified value is 1
Last but not least, our type system accepts recursive functions. For example, we have:
> let rec g x = if x < 1.0 then x else g (x
*
0.07) ;;
val g : real{+,0,53} -> real{+,0,53} = <fun>
> g 1.0 ;;
- : real{+,0,53} = 0.07000000000000
> g 2.0 ;;
Error: This expression has type real{+,1,53} but an expression was
expected of type real{+,0,53}
In the above session, the type system unifies the return type of the function with
the type of the conditional. The types of the then and else branches also need to be
unified. Then the return type is real{+,0,53} which corresponds to the type of the
180
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
180

value 1.0 used in the then branch. The type system also unifies the return type with
the type of the argument since the function is recursive. Finally, we obtain that the type
of g is real{+,0,53} -> real{+,0,53}. As a consequence, we cannot call g
with an argument whose ufp is greater than ufp(1.0) = 0. To overcome this limitation,
we introduce new comparison operations for real numbers. While the standard com-
parison operator < has type ’a -> ’a -> bool, the operator <{s,u,p} has type
real{s,u,p} -> real{s,u,p} -> bool. In other words, the compared value
are cast in the format {s, u, p} before performing the comparison. Now we can write
the code:
> let rec g x = if x <{
*
,10,15} 1.0 then x else g (x
*
0.07) ;;
val g : real{
*
,10,15} -> real{
*
,10,15} = <fun>
> g 2.0 ;;
- : real{
*
,10,15} = 0.1
> g 456.7 ;;
- : real{
*
,10,15} = 0.1
> g 4567.8 ;;
Error: This expression has type real{+,12,53} but an expression was
expected of type real{
*
,10,15}
Interestingly, unstable functions (for which the initial errors grow with the number
of iterations) are not typable. This is a desirable property of our system.
> let rec h n = if (n=0) then 1.0 else 3.33
*
(h (n -_ 1)) ;;
Error: This expression has type real{+,-1,-1} but an expression was
expected of type real{+,-3,-1}
Stable computations should be always accepted by our type system. Obviously, this
is not the case and, as any non-trivial type system, our type system rejects some cor-
rect programs. The challenge is then to accept enough programs to be useful from an
end-user point of view. We end this section by showing another example representa-
tive of what our type system accepts. More examples are given later in this article,
in Section 6. The example below deals with the implementation of the Taylor series
1
1−x
=
P
n≥0
x
n
. The implementation gives rise to a simple recursion, as shown in
the programming session below.
> let rec taylor x{
*
,-1,25} xn i n = if (i > n) then 0.0{
*
,10,20}
else xn + (taylor x (x
*
xn) (i +_ 1) n) ;;
val taylor : real{
*
,-1,25} -> real{
*
,10,20} -> int -> int -> real{
*
,10,20} = <fun>
> taylor 0.2 1.0 0 5;;
- : real{
*
,10,20} = 1.249
Obviously, our type system computes the propagation of the errors due to finite pre-
cision but does not take care of the method error intrinsic to the implemented algorithm
(the Taylor series instead of the exact formula
1
1−x
in our case.) All the programming
sessions introduced above as well as the additional examples of Section 6 are fully inter-
active in our system, Numl, i.e. the type judgments are obtained instantaneously (about
0.01 second in average following our measurements) including the most complicated
ones.
181
Numl - A Strongly Typed Language for Numerical Accuracy
181

3 The Type System
In this section, we introduce the formal definition of our type system for numerical
accuracy. First, in Section 3.1, we define the syntax of expressions and types and we in-
troduce a set of inference rules. Then we define in Section 3.2 the types of the primitives
for the operators among real numbers (addition, product, etc.) These types are crucial
in our system since they encode the propagation of the numerical accuracy information.
3.1 Expressions, Types and Inference Rules
In this section, we introduce the expressions, types and typing rules for our language.
For the sake of simplicity, the syntax introduced hereafter uses notations
`
a la lambda
calculus instead of the ML-like syntax employed in Section 2. In our system, expressions
and types are mutually dependent. They are defined inductively using the grammar of
Equation (3).
Expr 3 e ::= r{s, u, p} ∈ Real
u,p
| i ∈ Int | b ∈ Bool | id ∈ Id
| if e
0
then e
1
else e
2
| λx.e | e
0
e
1
| rec f x.e | t
Typ 3 t ::= | int | bool | real{i
0
, i
1
, i
2
} | α | Πx : e
0
.e
1
IExp 3 i ::= | int | op ∈ Id
I
| α | i
0
i
1
(3)
In Equation (3), the e terms correspond to expressions. Constants are integers i ∈ Int,
booleans b ∈ Bool and real numbers r{s, u, p} where r is the value itself, s ∈ Sign is
the sign as defined in Section 2 and u, p ∈ Int the ufp (see Equation (1)) and precision
of r. For inputs, the precision p is given by the user by means of annotations or chosen
by default by the system. Then p is inferred for the outputs of programs. The term p
defines the precision of r. Let ε(r) be the absolute error on r, we assume that
ε(r) < 2
u−p+1
. (4)
The errors on the numerical constants arising in programs are specified by the user or
determined by default by the system. The errors on the computed values can be inferred
by propagation of the initial errors.
In Equation (3), identifiers belong to the set Id and we assume a set of pre-defined
identifiers +, −, ×, ≤, =, . . . related to primitives for the logical and arithmetic opera-
tions. We write +, −, × and ÷ the operations on real numbers and + , − , × and ÷
the operations among integers. The language also admits conditionals, functions λx.e,
applications e
0
e
1
and recursive functions rec f x.e where f is the name of the func-
tion, x the parameter and e the body. The language of expressions also includes type
expressions t defined by the second production of the grammar of Equation (3).
The definition of expressions and type is mutually recursive. Type variables are
denoted α, β, . . . and Πx : e
0
.e
1
is used to introduce dependent types [22]. Let us
notice that our language does not explicitly contain function types t
0
→ t
1
since they
are encoded by means of dependent types. Let ≡ denote the syntactic equivalence, we
have
t
0
→ t
1
≡ Πx : t
0
.t
1
with x not free in t
1
. (5)
182
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
182

Γ ` i : int
(INT)
Γ ` b : bool
(BOOL)
sign(r) ≺ s ufp(r) ≤ u
Γ ` r{s,u,p} : real{s, u, p}
(REAL)
Γ (id) = t
Γ ` id : t
(ID)
Γ ` e
0
: bool Γ ` e
1
: t
1
Γ ` e
2
: t
2
t = t
1
t t
2
Γ ` if e
0
then e
1
else e
2
: t
(COND)
Γ, x : t
1
` e : t
2
Γ ` λx.e : Πx : t
1
.t
2
(ABS)
Γ, x : t
1
, f : Π.y : t
1
.t
2
` e : t
2
y not free in t
2
Γ ` rec f x.e : Πx : t
1
.t
2
(REC)
Γ ` e
1
: Πx : t
0
.t
1
Γ ` e
2
: t
2
t
2
v t
0
Γ ` e
1
e
2
: t
1
[x 7→ e
2
]
(APP)
Fig. 2. Typing rules for our language.
For convenience, we also write λx
0
.x
1
. . . x
n
.e instead of λx
0
.λx
1
. . . λx
n
.e and Πx
0
:
t
0
.x
1
: t
1
. . . x
n
: t
n
.e instead of Πx
0
: t
0
.Πx
1
: t
1
. . . Πx
n
: t
n
.e.
The types of constants are int, bool and real{i
0
, i
1
, i
2
} where i
0
, i
1
and i
2
are integer expressions denoting the format of the real number. Integer expressions of
IExpr ⊆ Expr are a subset of expressions made of integer numbers, integer primitives of
Id
I
⊆ Id (such as + , × , etc.), type variables and applications. Note that this definition
restricts significantly the set of expressions which may be written inside real types.
The typing rules for our system are given in Figure 2. These rules are mostly classi-
cal. The type judgment Γ ` e : t means that in the type environment Γ , the expression
e has type t. A type environment Γ : Id → Typ maps identifiers to types. We write
Γ x : t the environment Γ in which the variable x has type t. The typing rules (INT)
and (BOOL) are trivial. Rule (REAL) states that the type of a real number r{s,u,p}
is real{s, u, p} assuming that the actual sign of r is less than s and that the ufp of
r is less than u. Following Rule (ID), an identifier id has type t if Γ (id) = t. Rules
(COND), (ABS) and (REC) are standard rules for conditionals and abstractions respec-
tively. The rule for application, (APP), requires that the first expression e
1
has type
Πx : t
0
.t
1
(which is equivalent to t
0
→ t
1
if x is not free in t
1
) and that the argument
e
2
has some type t
2
v t
0
. The sub-typing relation @ is introduced for real numbers.
Intuitively, we want to allow the argument of some function to have a smaller ulp than
what we would require if we used t
0
= t
2
in Rule (APP), provided that the precision p
remains as good with t
2
as with t
0
. This relaxation allows to type more terms without
invalidating the type judgments. Formally, the relation v is defined by
real{s
1
, u
1
, p
1
} v real{s
2
, u
2
, p
2
} ⇐⇒ s
1
v s
2
∧ u
2
≥ u
1
∧ p
2
≤ u
2
−u
1
+p
1
.
(6)
In other words, the sub-typing relation of Equation (6) states that it is always correct to
add zeros before the first significant digit of a number, as illustrated in Figure 3.
3.2 Types of Primitives
In this section, we introduce the types of the primitives of our language. As mentionned
earlier, the arithmetic and logic operators are viewed as functional constants of the
language. The type of a primitive for an arithmetic operation among integers ∗ ∈
183
Numl - A Strongly Typed Language for Numerical Accuracy
183

u2
u1
0 0
p2
p1
Fig. 3. The sub-typing relation v of Equation (6).
{+ , − , × , ÷ } is
t
∗
= Πx : int.y : int.int . (7)
The type of comparison operators on∈ {=, 6=, <, >, ≤, ≥} are polymorphic with the
restriction that they reject the type real{s, u, p} which necessitates special comparison
operators:
t
on
= Πx : α.y : α.bool α 6= real{s, u, p} . (8)
For real numbers, we use comparisons at a given accuracy defined by the operators
on
{u,p}
∈ {<
{u,p}
, >
{u,p}
}. We have
t
on
{u,p}
= Πs : int, u : int, p : int.real{s, u, p + 1} → real{s, u, p + 1} → bool .
Notice that the operands of a comparison on
{u,p}
must have p + 1 bits of accuracy.
This is to avoid unstable tests, as detailed in the proof of Lemma 3 in Section 4. An
unstable test is a comparison between two approximate values such that the result of the
comparison is altered by the approximation error. For instance, if we reuse an example
of Section 2, in IEEE754 double precision, the condition 10
16
+ 1 = 10
16
evaluates
to true. We need to avoid such situations in our language in order to preserve our
subject reduction theorem (we need the control-flow be the same in the finite precision
and exact semantics). Let us also note that our language does not provide an equality
relation =
{u,p}
for real values. Again this is to avoid unstable tests. Given values x
and y of type real{s, u, p}, the programmer is invited to use |x− y| < 2
u−p+1
instead
of x = y in order to get rid of the perturbations of the finite precision arithmetic.
The types of primitives for real arithmetic operators are fundamental in our system
since they encode the propagation of the numerical accuracy information. They are
defined in figures 4 and 5. The type t
∗
of some operation ∗ ∈ {+, −, ×, ÷} is a pi-type
with takes six arguments s
1
, u
1
, p
1
, s
2
, u
2
and p
2
of type int corresponding to the sign,
ufp and precision of the two operands of ∗ and which produces a type
real{s
1
, u
1
, p
1
} → real{s
2
, u
2
, p
2
} → real{S
∗
(s
1
, s
2
), U
∗
(s
1
, u
1
, s
2
, u
2
), P
∗
(u
1
, p
1
, u
2
, p
2
)}
(9)
where S
∗
, U
∗
and P
∗
are functions which compute the sign, ufp and precision of the
result of the operation ∗ in function of s
1
, u
1
, p
1
, s
2
, u
2
and p
2
. These functions extend
the functions used in [16].
The functions S
∗
determine the sign of the result of an operation in function of the
signs of the operands and, for additions and subtractions, in function of the ufp of the
operands. The functions U
∗
compute the ufp of the result. Notice that U
+
and U
−
use
184
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
184

t
∗
= Πs
1
: int, u
1
: int, p
1
: int, s
2
: int, u
2
: int, p
2
: int.
real{s
1
, u
1
, p
1
} → real{s
2
, u
2
, p
2
}
→ real{S
∗
(s
1
, u
1
, s
2
, u
2
), U
∗
(s
1
, u
1
, s
2
, u
2
), P
∗
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
)}
U
+
(s
1
, u
1
, s
2
, u
2
)) = max(u
1
, u
2
) + σ
+
(s
1
, s
2
)
P
+
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) = max(u
1
, u
2
) + σ
+
(s
1
, s
2
)−
max(u
1
− p
1
, u
2
− p
2
) − ι(u
1
− p
1
, u
2
− p
2
)
U
−
(s
1
, u
1
, s
2
, u
2
)) = max(u
1
, u
2
) + σ
−
(s
1
, s
2
)
P
−
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) = max(u
1
, u
2
) + σ
−
(s
1
, s
2
)−
max(u
1
− p
1
, u
2
− p
2
) − ι(u
1
− p
1
, u
2
− p
2
)
U
×
(s
1
, u
1
, s
2
, u
2
)) = u
1
+ u
2
+ 1
P
×
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) = u
1
+ u
2
+ 1−
max(u
1
+ u
2
+ 1 − p
1
, u
1
+ u
2
+ 1 − p
2
) − ι(p
1
, p
2
)
U
÷
(s
1
, u
1
, s
2
, u
2
)) = u
1
− u
2
+ 1
P
÷
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) = P
×
(u
1
, p
1
, u
2
, p
2
) − 1 ι(x, y) =

1 if x = y,
0 otherwise.
Fig. 4. Types of the primitives corresponding to the elementary arithmetic operations ∗ ∈
{+, −, ×, ÷}. The functions S
∗
and σ
∗
are defined in Figure 5.
the functions σ
+
and σ
−
, respectively. These functions are defined in the bottom right
corner of Figure 5 to increment the ufp of the result of some addition or subtraction
in the relevant cases only. For example if a and b are two positive real numbers then
ufp(a + b) is possibly max

ufp(a), ufp(b)

+ 1 but if a > 0 and b < 0 then ufp(a + b)
is not greater than max

ufp(a), ufp(b)

. The functions P
∗
compute the precision of the
result. Basically, they compute the number of bits between the ufp and the ulp of the
result.
We end this section by exhibiting some properties of the functions P
∗
. Let ε(x)
denote the error on x ∈ Real
u,p
. We have ε(x) < 2
u−p+1
= ulp(x). Let us start with
addition. Lemma 1 relates the accuracy of the operands to the accuracy of the result of
an addition between two values x and y. Lemma 2 is similar to Lemma 1 for product.
Lemma 1. Let x and y be two values such that ε(x) < 2
u
1
−p
1
+1
and ε(y) < 2
u
2
−p
2
+1
.
Let z = x + y,
u = U
+
(s
1
, u
1
, s
2
, u
2
)
p = P
+
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) .
(10)
Then ε(z) < 2
u−p+1
.
Proof. The errors on addition may be bounded by e
+
= ε(x)+ε(y). Then the most sig-
nificant bit of the error has weight ufp(e
+
) and the accuracy of the result is p = ufp(x+
y) − ufp(e
+
). Let u = ufp(x + y) = max(u
1
, u
2
) + σ
+
(s
1
, s
2
) = U
+
(s
1
, u
1
, s
2
, u
2
).
We need to over-approximate e
+
in order to ensure p. We have ε(x) < 2
u
1
−p
1
+1
and
ε(y) < 2
u
2
−p
2
+1
and, consequently, e
+
< 2
u
1
−p
1
+1
+ 2
u
2
−p
2
+1
. We introduce the
function ι(x, y) also defined in Figure 4 and which is equal to 1 if x = y and 0 other-
wise. We have
ufp(e
+
) < max(u
1
− p
1
+ 1, u
2
− p
2
+ 1) + ι(u
1
− p
1
, u
2
− p
2
)
≤ max(u
1
− p
1
, u
2
− p
2
) + ι(u
1
− p
1
, u
2
− p
2
)
185
Numl - A Strongly Typed Language for Numerical Accuracy
185

S
+
S
×
and S
÷
s
1
\s
2
0 + − >
0
0 + − >
+ + +
+ if u
1
< u
2
− if u
2
< u
1
> otherwise
>
− −
+ if u
2
< u
1
− if u
1
< u
2
> otherwise
− >
>
> > > >
s
1
\s
2
0 + − >
0
0 0 0 0
+
0 + − >
−
0 − + >
>
0 > > >
S
−
s
1
\s
2
0 + − >
0
0 − + >
+ +
− if u
1
< u
2
+ if u
2
< u
1
> otherwise
+ >
− − −
− if u
2
< u
1
+ if u
1
< u
2
> otherwise
>
>
> > > >
σ
+
0 + − >
0 0 0 0 0
+ 0 1 0 1
− 0 0 1 1
> 0 1 1 1
σ
−
0 + − >
0 0 0 0 0
+ 0 0 1 1
− 0 1 0 1
> 0 1 1 1
Fig. 5. Operators used in the types of the primitives of Figure 4.
Let us write p = max(u
1
−p
1
, u
2
−p
2
)−ι(u
1
−p
1
, u
2
−p
2
) = P
+
(s
1
, u
1
, p
1
s
2
, u
2
, p
2
).
We conclude that u = U
+
(s
1
, u
1
, s
2
, u
2
), p = P
+
(s
1
, u
1
, p
1
s
2
, u
2
, p
2
) and ε(z) <
2
u−p+1
. 
Lemma 2. Let x and y be two values such that ε(x) < 2
u
1
−p
1
+1
and ε(y) < 2
u
2
−p
2
+1
.
Let z = x × y, u = U
×
(s
1
, u
1
, s
2
, u
2
) and p = P
×
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
). Then
ε(z) < 2
u−p+1
.
Proof. For product, we have p = ufp(x × y) − ufp(e
×
) with e
×
= x · ε(y) + y · ε(x) +
ε(x) · ε(y). Let u = u
1
+ u
2
+ 1 = U
×
(s
1
, u
1
, s
2
, u
2
). We have, by definition of ufp,
2
u
1
≤ x < 2
u
1
+1
and 2
u
2
≤ y < 2
u
2
+1
. Then e
×
may be bounded by
e
×
< 2
u
1
+1
· 2
u
2
−p
2
+1
+ 2
p
2
+1
· 2
u
1
−p
1
+1
+ 2
u
1
−p
1
+1
· 2
u
2
−p
2
+1
= 2
u
1
+u
2
−p
2
+2
+ 2
u
1
+u
2
−p
1
+2
+ 2
u
1
+u
2
−p
1
−p
2
+2
.
(11)
Since u
1
+u
2
−p
1
−p
2
+2 < u
1
+u
2
−p
1
+2 and u
1
+u
2
−p
1
−p
2
+2 < u
1
+u
2
−p
2
+2,
we may get rid of the last term of Equation (11) and we obtain that
ufp(e
×
) < max(u
1
+ u
2
− p
1
+ 2, u
1
+ u
2
− p
2
+ 2) + ι(p
1
, p
2
)
≤ max(u
1
+ u
2
− p
1
+ 1, u
1
+ u
2
− p
2
+ 1) + ι(p
1
, p
2
) .
Let us write p = max(u
1
+u
2
−p
1
+1, u
1
+u
2
−p
2
+1)−ι(p
1
, p
2
) = P
×
(s
1
, u
1
, p
1
s
2
,
u
2
, p
2
). Then u = U
×
(s
1
, u
1
, s
2
, u
2
), p = P
×
(s
1
, u
1
, p
1
s
2
, u
2
, p
2
) and ε(z) < 2
u−p+1
.

186
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
186

Note that, by reasoning on the exponents of the values, the constraints resulting
from a product become linear. The equations for subtraction and division are almost
identical to the equations for addition and product, respectively. Note that the result of
a division has one less bit than the result of a product. This is due to the fact that, even
if the operands are finite numbers, the result of the division may be irrational and pos-
sibly needs to be truncated. We conclude this section with the following theorem which
summarize the properties of the types of the result of the four elementary operations.
Theorem 1. Let x and y be two values such that ε(x) < 2
u
1
−p
1
+1
and ε(y) <
2
u
2
−p
2
+1
and let ∗ ∈ {+, −, ×, ÷} be an elementary operation. Let z = x ∗ y, let
u = U
∗
(s
1
, u
1
, s
2
, u
2
) ,
p = P
∗
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) .
(12)
Then ε(z) < 2
u+p−1
.
Proof. The cases of addition and product correspond to Lemma 1 and Lemma 2, respectively.
The cases of subtraction and division are similar. 
Numl uses a modified Hindley-Milner type inference algorithm. Linear constraints
among integers are generated (even for non linear expressions). They are solvd using
a SMT solver. For space limitation reasons, the details of this algorithm are out of the
scope of this articl e.
4 Soundness of the Type System
In this section, we introduce a subject reduction theorem proving the consistency of
our type system. We use two operational semantics →
F
and →
R
for the finite precision
and exact arithmetics, respectively. The exact semantics is used for proofs. Obviously,
in practice, only the finite precision semantics is implemented. We write → whenever
a reduction rule holds for both →
F
and →
R
(in this case, we assume that the same
semantics →
F
or →
R
is used in the lower and upper parts of the same sequent). Both
semantics are displayed in Figure 6. They concern the subset of the language of Equa-
tion (3) which do not deal with types.
EvalExpr 3 e ::= r{s, u, p} ∈ Real
u,p
| i ∈ Int | b ∈ Bool | id ∈ Id
| if e
0
then e
1
else e
2
| λx.e | e
0
e
1
| rec f x.e| e
0
∗ e
1
.
(13)
In Equation (13), ∗ denotes an arithmetic operator ∗ ∈ {+, −, ×, ÷, + , − , × ,
÷ }. In Figure 6, Rule (FVAL) of →
F
transforms a syntactic element describing a real
number r{s, u, p} in a certain format into a value v
F
. The finite precision value v
F
is an
approximation of r with an error less than the ulp of r{s, u, p}. In the semantics →
R
,
the real number r{s, u, p} simply produces the value r without any approximation by
Rule (RVal). Rules (Op1) and (Op2) evaluate the operands of some binary operation
and Rule (Op) performs an operation ∗ ∈ {+, −, ×, ÷, + , − , × , ÷ } between two
values v
0
and v
1
.
187
Numl - A Strongly Typed Language for Numerical Accuracy
187

|r − v
F
| < 2
u−p+1
ufp(r) ≤ u sign(v
F
) ≺ s
r{s, u, p} →
F
v
F
(FVal)
v
R
= r
r{s, u, p} →
R
v
R
(RVal)
e
0
→ e
0
0
e
0
∗ e
1
→ e
0
0
∗ e
1
(Op1)
e
1
→ e
0
1
v ∗ e
1
→ v ∗ e
0
1
(Op2) ∗ ∈ {+, −, ×, ÷, + , − , × , ÷ }
v = v
0
∗ v
1
v
0
∗ v
1
→ v
(Op) ∗ ∈ {+, −, ×, ÷, + , − , × , ÷ } rec f x.e → λx.ehrec f x.e/f i (REC)
e
0
→ e
0
0
e
0
on e
1
→ e
0
0
on e
1
(Cmp1)
e
1
→ e
0
1
v on e
1
→ v on e
0
1
(Cmp2) on∈ {<
{u,p}
, >
{u,p}
, <, >}
b = (2
u−p+1
on v
F
1
− v
F
0
)
v
0
on
{u,p}
v
1
→
F
b
(FCmp)
b = (v
0
on v
1
)
v
0
on
{u,p}
v
1
→
R
b
(RCmp) on∈ {<
{u,p}
, >
{u,p}
}
e
1
→ e
0
1
e
0
e
1
→ e
0
e
0
1
(App1)
e
0
→ e
0
0
e
0
v → e
0
0
v
(App2) (λx.e) v → ehv/xi (Red)
b = v
0
on v
1
v
0
on v
1
→ b
on∈ {=, 6=, <, >, ≤, ≥}
e
0
→ e
0
0
if e
0
then e
1
else e
2
→ if e
0
0
then e
1
else e
2
(Cond)
v = true
if v then e
1
else e
2
→ e
1
(CondTrue)
v = false
if v then e
1
else e
2
→ e
2
(CondFalse)
Fig. 6. Operational semantics for our language.
Rules (Cmp1), (Cmp2) and (ACmp) deal with comparisons. They are similar to
Rules (Op1), (Op2) and (Op) described earlier. Note that the operators <, >, =, 6=
concerned by Rule (ACmp) are polymorphic except that they do not accept arguments
of type real. Rules (FCmp) and (RCmp) are for the comparison of real values.
Rule (FCmp) is designed to avoid unstable tests by requiring that the distance between
the two compared values is greater than the ulp of the format in which the comparison
is done. With this requirement, a condition cannot be invalidated by the roundoff errors.
Let us also note that, with this definition, x <
u,p
y 6⇒ y >
u,p
x or x >
u,p
y 6⇒ y <
u,p
x. For the semantics →
R
, Rule (RCmp) simply compares the exact values.
The other rules are standard and are identical in →
F
and →
R
. Rules (App1), (App2)
and (Red) are for applications and Rule (Rec) is for recursive functions. We write
ehv/xi the term e in which v has been substituted to the free occurrences of x. Rules
(Cond), (CondTrue) and (CondFalse) are for conditionals.
The rest of this section is dedicated to our subject reduction theorem. First of all,
we need to relate the traces of →
F
and →
R
. We introduce new judgments
Γ |= (e
F
, e
R
) : t . (14)
Intuitively, Equation (14) means that expression e
F
simulates e
R
up to accuracy t. In
this case, e
F
is syntactically equivalent to e
R
up to the values which, in e
F
, are approxi-
mations of the values of e
R
. The value of the approximation is given by type t.
188
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
188

Γ |= (i, i) : int
(INT)
Γ |= (b, b) : bool
(BOOL)
Γ (id) = t
Γ |= (id, id) : t
(ID)
sign(r) ≺ s ufp(r) ≤ u
Γ |= (r{s,u,p}, r{s,u,p}) : real{s, u, p}
(SREAL)
|v
R
− v
F
| < 2
u−p+1
Γ |= (v
F
, v
R
) : real{s, u, p}
(VREAL)
Γ |= (e
1F
, e
1R
) : real{s
1
, u
1
, p
1
} Γ |= (e
2F
, e
2R
) : real{s
1
, u
1
, p
1
} ∗ ∈ {+, −, ×, ÷}
Γ |= (e
1F
∗ e
2F
, e
1R
∗ e
2R
) : real{S
∗
(s
1
, u
1
, s
2
, u
2
), U
∗
(s
1
, u
1
, s
2
, u
2
), P
∗
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
)}
(ROP)
Γ |= (e
1F
, e
1R
) : real{s
1
, u, p + 1} Γ |= (e
2F
, e
2R
) : real{s
1
, u, p + 1} ∗ ∈ {<, >}
Γ |= (e
1F
on
u,p
e
2F
, e
1R
on
u,p
e
2R
) : bool
(RCMP)
Γ |= (e
1F
, e
1R
) : int Γ |= (e
2F
, e
2R
) : int ∗ ∈ {+ , − , × , ÷ }
Γ |= (e
1F
∗ e
2F
, e
1R
∗ e
2R
) : int
(INTOP)
Γ |= (e
1F
, e
1R
) : t Γ |= (e
2F
, e
2R
) : t t 6= real{s, u, p} on∈ {=, 6=, <, >, ≤, ≥}
Γ |= (e
1F
on e
2F
, e
1R
on e
2R
) : bool
(ACMP)
Γ |= (e
0F
, e
0R
) : bool Γ |= (e
1F
, e
1R
) : t
1
Γ |= (e
2F
, e
2R
) : t
2
t = t
1
t t
2
Γ |= (if e
0F
then e
F
1 else e
2F
, if e
0R
then e
1R
else e
2R
) : t
(COND)
Γ, x : t
1
|= (e
F
, e
R
) : t
2
Γ |= (λx.e
F
, λx.e
R
) : Πx : t
1
.t
2
(ABS)
Γ, x : t
1
, f : Π.y : t
1
.t
2
|= (e
F
, e
R
) : t
2
Γ |= (rec f x.e
F
, rec f x.e
R
) : Πx : t
1
.t
2
(REC)
Γ |= (e
1F
, e
1R
) : Πx : t
0
.t
1
Γ |= (e
2F
, e
2R
) : t
2
t
2
v t
0
Γ |= (e
1F
e
2F
, e
1R
e
2R
) : t
1
[x 7→ e
2
]
(APP)
Fig. 7. Simulation relation |= used in our subject reduction theorem.
Formally, |= is defined in Figure 7. These rules are similar to the typing rules of
Figure 2 excepted that they operate on pairs (e
F
, e
R
). They are also designed for the
language of Equation (13) and, consequently, deal with the elementary arithmetic oper-
ations +, −, × and ÷ as well as the comparison operators. The difference between the
rules of Figure 2 and Figure 7 is in Rule (VReal) which states that a real value v
R
is
correctly simulated by a value v
F
up to accuracy real{s, u, p} if |v
R
− v
F
| < 2
u−p+1
.
It is easy to show, by examination of the rules of Figure 2 and Figure 7 that
Γ |= (e
F
, e
R
) : t =⇒ Γ ` e
F
: t . (15)
We introduce now Lemma 3 which asse rts the soundness of the type system for
one reduction step. Basically, this lemma states that types are preserved by reduction
and that concerning the values of type real, the distance between the finite precision
value and the exact value is less than the ulp given by the type.
Lemma 3 (Weak subject reduction). If Γ |= (e
F
, e
R
) : t and if e
F
→
F
e
0
F
and
e
R
→
R
e
0
R
then Γ |= (e
0
F
, e
0
R
) : t.
Proof. By induction on the structure of expressions and case examination on the possible tran-
sition rules of Figure 6.
189
Numl - A Strongly Typed Language for Numerical Accuracy
189

– If e
F
≡ e
R
≡ r{s, u, p} then Γ |= (r{s,u,p}, r{s,u,p}) : real{s, u, p} and, from
the reduction rules (FVal) and (RVal) of Figure 6, r{s, u, p} →
F
v
F
and r{s, u, p} →
R
v
R
with |v
F
− v
R
| < 2
u−p+1
. So Γ |= (v
F
, v
R
) : real{s, u, p}.
– If e
F
≡ e
0F
∗ e
1F
and e
R
≡ e
0R
∗ e
1R
then several cases must be distinguished.
• If e
F
≡ v
0F
∗ v
1F
and e
R
≡ v
0R
∗ v
1R
then, by induction hypothesis, Γ |= (v
0F
, v
0R
) :
real{s
0
, u
0
, p
0
}, Γ |= (v
1F
, v
1R
) : real{s
1
, u
1
, p
1
} and, consequently, from Rule
(VREAL),
|v
0R
− v
0F
| < 2
u
0
−p
0
+1
and |v
1R
− v
1F
| < 2
u
1
−p
1
+1
. (16)
Following Figure 4, the type t of e is
t =

Πs
1
: int, u
1
: int, p
1
: int, s
2
: int, u
2
: int, p
2
: int.
real{s
1
, u
1
, p
1
} → real{s
2
, u
2
, p
2
} →
→ real{S
∗
(s
1
, u
1
, s
2
, u
2
), U
∗
(s
1
, u
1
, s
2
, u
2
), P
∗
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
)}

s
1
u
1
p
1
s
2
u
2
p
2
,
= real{S
∗
(s
1
, u
1
, s
2
, u
2
), U
∗
(s
1
, u
1
, s
2
, u
2
), P
∗
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
)}
= real{s, u, p}
By Rule (OP), e →
F
v
F
and e →
R
v
R
and, by Theorem 1, with the assumptions of
Equation (16), we know that |v
R
− v
F
| < 2
u−p+1
. Consequently, Γ |= (v
F
, v
R
) :
real{s, u, p}.
• If e
F
≡ v
0F
∗ v
1F
and e
R
≡ v
0R
∗ v
1R
with Γ |= (v
0
, v
1
) : int then, by Rule
(Op), e → (v, v) and, by Equation (7), Γ ` v : int. If e ≡ e
0
∗ e
1
then, by Rule
(Op1), e → e
0
∗ e
0
1
and we conclude by induction hypothesis. The case e ≡ e
0
∗ v
1
is
similar to the former one.
– If e
F
≡ e
0F
on
u,p
e
1F
and e
R
≡ e
0R
on
u,p
e
1R
then several cases have to be examined.
• If e
F
≡ v
0F
on
u,p
v
1F
and e
R
≡ v
0R
on
u,p
v
1R
then by rules (FCmp) and (RCmp)
e
F
→
F
b
F
, e
R
→
R
b
R
with b
F
= v
0F
− v
1F
on
{u,p}
2
u−p+1
and b
R
= v
0R
− v
1R
on
{u,p}
0. By rule (RCmp) of Figure 7, Γ |= (v
0F
, v
1F
) : real{s, u, p} and Γ |= (v
0R
, v
1R
) :
real{s, u, p}. Consequently, |v
0R
− v
0F
| < 2
u−p+1
and |v
1R
− v
1F
| < 2
u−p+1
. By
combining the former equations, we obtain that |(v
0R
− v
1R
) − (v
0F
− v
1F
)| < 2
u−p
.
Consequently, b
F
= b
R
and we conclude that Γ |= (b
F
, b
R
) : bool.
• The other cases for e
F
≡ e
0F
on
u,p
e
1F
are similar to the cases e
F
≡ v
0F
∗ v
1F
examined
previously.
– The other cases simply follow the structure of the terms, by application of the induction
hypothesis. 
Let →
∗
F
(resp. →
∗
R
) denote the reflexive transitive closure of →
F
(resp. →
R
). Theo-
rem 2 expresses the soundness of our type system for sequences of reduction of arbitrary
length.
Theorem 2 (Subject reduction). If Γ |= (e
F
, e
R
) : t and if e
F
→
∗
F
e
0
F
and e
R
→
∗
R
e
0
R
then Γ |= (e
0
F
, e
0
R
) : t.
Proof. By induction on the length of the reduction sequence, using Lemma 3. 
Theorem 2 asserts the soundness of our type system. It states that the evaluation of
an expression of type real{s, u, p} yields a result of accuracy 2
u−p+1
.
190
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
190

let rec unifyReal s
1
u
1
p
1
s
2
u
2
p
2
= match (!s
1
,!u
1
,!p
1
) with
(int(s
1
0
),int(u
1
0
),int(p
1
0
)) →
(match (!s
2
,!u
2
,!p
2
) with
(int(s
2
0
),int(u
2
0
),int(p
2
0
)) →
let s = if (s
1
0
=s
2
0
) then s
1
0
else 2 in
let u = max u
1
0
u
2
0
in
let p = if (u
1
0
>=u
2
0
) then min p
1
0
(u
1
0
- u
2
0
+ p
2
0
)
else min p
2
0
(u
2
0
- u
1
0
+ p
1
0
)
in if (p>0) then
(s
1
:= int(s) ; s
2
:= int(s) ; u
1
:= int(u) ;
u
2
:= int(u) ; p
1
:= int(p) ; p
2
:= int(p))
else raise (Error ("Type "
ˆ(printExpr (TFloat(s
1
,u
1
,p
1
)))ˆ" is not compatible
with type "ˆ(printExpr (TFloat(s
2
,u
2
,p
2
))) ) )
| (TypeVar(refS,strS),TypeVar(refU,strU),
TypeVar(refP,strP)) → refS := Some(!s
1
) ;
refU := Some(!u
1
) ; refP := Some(!p
1
)
| _ → solveLT !s
1
!s
2
!u
1
!u
2
!p
1
!p
2
)
| (TypeVar(refS,strS),TypeVar(refU,strU),
TypeVar(refP,strP)) →
((match !refS with
None → refS := Some(!s
2
)
| Some(s
1
) → unify s
1
!s
2
) ;
(match !refU with
None → refU := Some(!u
2
)
| Some(u
1
) → unify u
1
!u
2
) ;
(match !refP with
None → refP := Some(!p
2
)
| Some(p
1
) → unify p
1
!p
2
)
)
| _ → (match (!s
2
,!u
2
,!p
2
) with
(TypeVar(refS,strS),TypeVar(refU,strU),
TypeVar(refP,strP)) →
similar to previous case
| _ → if ((s
1
=s
2
) && (u
1
=u
2
) && (p
1
=p
2
)) then ()
else solve !s
1
!s
2
!u
1
!u
2
!p
1
!p
2
)
Fig. 8. Unification procedure for types real.
5 Type System Implementation
In this section, we give some details about the implementation of our type system in
Numl. Section 5.1 deals with the unification algorithm and Section 6 presents examples
of typable programs in complement to the introductory examples of Section 2.
191
Numl - A Strongly Typed Language for Numerical Accuracy
191

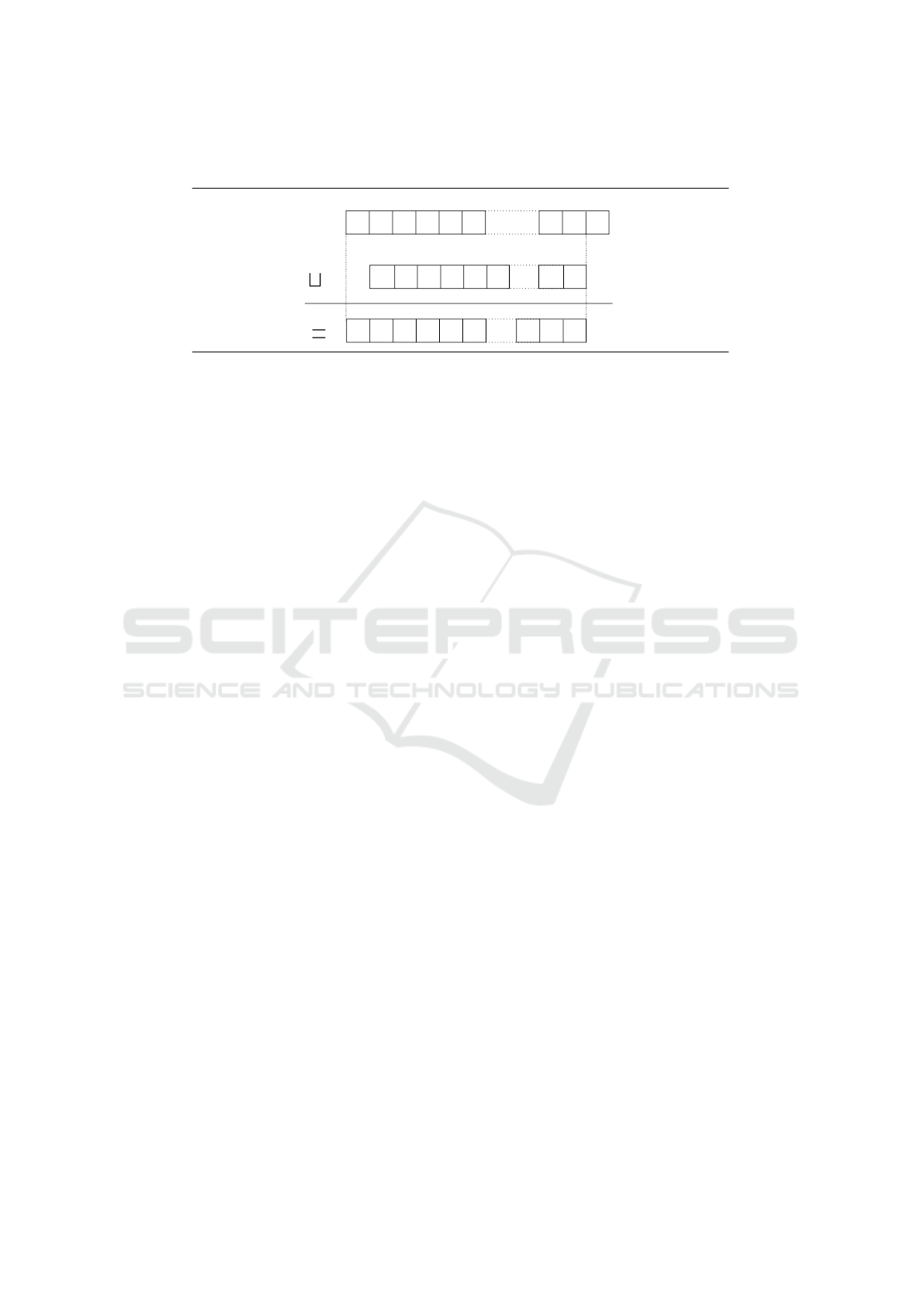
Fig. 9. The supremum operator t of Equation (17).
5.1 Unification Algorithm
In this section, we describe how the type system introduced in Section 3 is implemented.
Basically, we use a unification-based type inference in which type variables are repre-
sented by reference cells. The type real also stores the format {s, u, p} into reference
cells, so that it can be modified when unifying two terms of type real.
The type inference and unification algorithms are classical excepted for the unifi-
cation of two real types, done by the function unifyReal displayed in Figure 8
and which requires, in certain cases, a call to a SMT solver (in practice we use Z3
[18]). The function unifyReal takes as arguments the formats φ
1
= {s
1
, u
1
, p
1
} and
φ
2
= {s
2
, u
2
, p
2
} of the types to be unified.
The function unifyReal calls in a mutually recursive way the function unify
on terms. It also refers to type variables correspndig the constructor TypeVar. The
fields of TypeVar are the value itself and a string corrsponding to the name of the
variable. The value may be either None when the type variable is not constrained or
some reference to an expression when a type has been given to the variable by unifica-
tion. The function solve performs a partial evaluation of the expressions occurring in
the equations, in order to simplify them, translates them for Z3, calls the SMT solver
and then assign the values of the solution to the relevant type variables. The function
solveLT acts just like the function solve but requires that the precision of the sec-
ond expression is greater than or equal to the precision of the first expression instead of
a strict equality. Several cases are distinguished in the function unifyReal of Figure
8:
– If φ
1
and φ
2
are fully instantiated, i.e. s
i
, u
i
and p
i
, 1 ≤ i ≤ 2 are integers then we
assign φ = φ
1
tφ
2
to φ
1
and φ
2
. The supremum t refers to the order v introduced
in Equation (6). Formally, we have:
φ
1
t φ
2
=

s
1
] s
2
, max(u
1
, u
2
), p

with p =

min(p
1
, u
1
− u
2
+ p
2
) if u
1
≥ u
2
,
min(p
2
, u
2
− u
1
+ p
1
) otherwise .
(17)
In Equation (17), ] computes the supremum of to values of Sign. Figure 9 illus-
trates the effect of the operator t.
– If φ
1
is fully instantiated and φ
2
is made of three type variables then φ
1
is assigned
to φ
2
.
192
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
192

– If φ
1
is fully instantiated and φ
2
is neither fully instantiated or a triple of type
variables then φ − 2 is made of three integer expressions containing type variables,
φ
2
= {e
0
, e
1
, e
2
}. We have to solve the system
(S) :



s
1
= e
0
u
1
= e
1
p
1
= e
2
. (18)
We call the SMT solver Z3 to solve this system of equation. Recall that e
0
, e
1
and
e
2
come from the types of primitives introduced in Figure 4. These expressions are
linear and are easy to solve for an SMT solver.
– If both φ
1
and φ
2
are made of type variables then we identify them in a pairwise
manner.
– If both φ
1
and φ
2
are integer expressions then φ
1
= {e
0
, e
1
, e
2
} and φ
2
= {e
0
0
, e
0
1
, e
0
2
}.
We have to solve the system
(S) :



e
0
= e
0
0
e
1
= e
0
1
e
2
= e
0
2
. (19)
Again, we call Z3 to solve this system of linear equations.
– The other cases are symmetric to the ones detailled formerly, they are treated simi-
larly.
For example, the equations sent to the SMT solver for the call newton 9.0 0.0
g gprime ;; to the newton function of Section 2 are given in Equation (20).
(S) :























S
+
(
0
a, max(
0
b, −7) + S
×
(
0
a, 1), 1, −7) = 2
(max(
0
b, −7) + S
×
(S
+
(
0
a,
0
b, 1, −7), 1) = 10
max(max(
0
b, −7) + S
×
(S
+
(
0
a,
0
b, 1, −7), 1), −7)
+S
×
(S
+
(
0
a, max(
0
b, −7) + S
×
(
0
a, 1), 1, −7), 1)
− max(max(
0
b, −7) + S
×
(S
+
(
0
a,
0
b, 1, −7), 1) −
0
c, −60)
−ι(max(
0
b, −7) + S
×
(S
+
(
0
a,
0
b, 1, −7), 1) −
0
c, −60) ≤ 21
(20)
These equations are encoded in Z3 by expanding the operators max, S
+
, S
×
, and ι
following the definitions of Figure 4. For example, the Z3 encoding of the first equality
of Equation (20) is displayed in Figure 10. Globally, the encoding of the three equations
of Equation (20) is a 1007 lines long Z3 file. Z3 solves these equations in 0.215 seconds
(average measured time on 5 executions).
6 Experiments
In this section, we report some experiments showing how our type system behaves in
practice. Section 6.1 presents Numl implementations of usual mathematical formulas
while Section 6.2 introduce a larger example demonstrating the expressive power of our
type system.
193
Numl - A Strongly Typed Language for Numerical Accuracy
193

(assert (= 2
(ite (and (= a 0) (= 1 0)) 0
(ite (and (= a 1) (= 1 1)) 1
(ite (and (= a -1) (= 1 -1)) -1
(ite (and (= a 1) (= 1 0)) 1
(ite (and (= a 0) (= 1 1)) 1
(ite (and (= a -1) (= 1 0)) -1
(ite (and (= a 0) (= 1 -1)) -1
(ite (and (= a 1) (= 1 -1))
(ite (> (+ (ite (>= b -7) b -7)
(ite (and (= a 0) (= 1 0)) 0
(ite (and (= a 1) (= 1 -1)) -1
(ite (and (= a -1) (= 1 1)) -1
(ite (and (= a -1) (= 1 -1)) 1
(ite (and (= a 1) (= 1 1)) 1
(ite (and (= a 1) (= 1 0)) 0
(ite (and (= a 0) (= 1 1)) 0
(ite (and (= a -1) (= 1 0)) 0
(ite (and (= a 0) (= 1 -1)) 0
2)))))))))) -7) 1
(ite (< (+ (ite (>= b -7) b -7)
(ite (and (= a 0) (= 1 0)) 0
(ite (and (= a 1) (= 1 -1)) -1
(ite (and (= a -1) (= 1 1)) -1
(ite (and (= a -1) (= 1 -1)) 1
(ite (and (= a 1) (= 1 1)) 1
(ite (and (= a 1) (= 1 0)) 0
(ite (and (= a 0) (= 1 1)) 0
(ite (and (= a -1) (= 1 0)) 0
(ite (and (= a 0) (= 1 -1)) 0
2)))))))))) -7) -1 2))
(ite (and (= a -1) (= 1 1))
(ite (< (+ (ite (>= b -7) b -7)
(ite (and (= a 0) (= 1 0)) 0
(ite (and (= a 1) (= 1 -1)) -1
(ite (and (= a -1) (= 1 1)) -1
(ite (and (= a -1) (= 1 -1)) 1
(ite (and (= a 1) (= 1 1)) 1
(ite (and (= a 1) (= 1 0)) 0
(ite (and (= a 0) (= 1 1)) 0
(ite (and (= a -1) (= 1 0)) 0
(ite (and (= a 0) (= 1 -1)) 0
2)))))))))) -7) 1
(ite (> (+ (ite (>= b -7) b -7)
(ite (and (= a 0) (= 1 0)) 0
(ite (and (= a 1) (= 1 -1)) -1
(ite (and (= a -1) (= 1 1)) -1
(ite (and (= a -1) (= 1 -1)) 1
(ite (and (= a 1) (= 1 1)) 1
(ite (and (= a 1) (= 1 0)) 0
(ite (and (= a 0) (= 1 1)) 0
(ite (and (= a -1) (= 1 0)) 0
(ite (and (= a 0) (= 1 -1)) 0
2)))))))))) -7) -1 2))
2)))))))))))
Fig. 10. Z3 encoding of the first equality of Equation (20).
6.1 Usual Mathematical Formulas
Our first examples concern usual mathematical formulas, to compute the volume of
geometrical objects or formulas related to polynomials. These examples aim at showing
that usual mathematical formulas are typable in our system. We start with the volume
of the sphere and of the cone.
> let sphere r = (4.0 / 3.0)
*
3.1415926{+,1,20}
*
r
*
r
*
r ;;
val sphere : real{’a,’b,’c} -> real{<expr>,<expr>,<expr>} = <fun>
> sphere 1.0 ;;
- : real{+,7,20} = 4.188
> let cone r h = (3.1415926{+,1,20}
*
r
*
r
*
h) / 3.0 ;;
val cone : real{’a,’b,’c} -> real{’a,’b,’c}
-> real{<expr>,<expr>,<expr>} = <fun>
> cone 1.0 1.0 ;;
- : real{+,4,20} = 1.0472
We repeatedly define the function sphere with more precision in order to show the
impact on the accuracy of the results. Note that the results now have 15 digits instead
of the former 5 digits.
194
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
194

> let sphere r = (4.0 / 3.0)
*
3.1415926535897932{+,1,53}
*
r
*
r
*
r ;;
val sphere : real{’a,’b,’c} -> real{<expr>,<expr>,<expr>} = <fun>
> sphere 1.0 ;;
- : real{+,7,52} = 4.1887902047863
The next examples concern polynomials. We start with the computation of the dis-
criminant of a second degree polynomial.
> let discriminant a b c = b
*
b - 4.0
*
a
*
c ;;
val discriminant : real{’a,’b,’c} -> real{’d,’e,’f} -> real{’g,’h,’i}
-> real{<expr>,<expr>,<expr>} = <fun>
> discriminant 2.0 -11.0 15.0 ;;
- : real{+,8,52} = 1.000000000000
Our last example concerning usual formulas is the Taylor series development of
the sine function. In the code below, observe that the accuracy of the result is corre-
lated to the accuracy of the argument. As mentioned in Section 2, error methods are
neglected, only the errors due to the finite precision are calculated (indeed, sin
π
8
=
0.382683432 . . .).
let sin x = x - ((x
*
x
*
x) / 3.0) + ((x
*
x
*
x
*
x
*
x) / 120.0) ;;
val sin : real{’a,’b,’c} -> real{<expr>,<expr>,<expr>} = <fun>
> sin (3.14{1,6} / 8.0) ;;
- : real{
*
,0,6} = 0.3
> sin (3.14159{1,18} / 8.0) ;;
- : real{
*
,0,18} = 0.37259
6.2 Newton-Raphson Method
In this section, we introduce a larger example to compute the zero of a function using the
Newton-Raphson method. This example, which involves several higher order functions,
shows the expressiveness of our type system. In the programming session below, we
first define a higher order function deriv which takes as argument a function and
computes its numerical derivative at a given point. Then we define a function g and
compute the value of its derivative at point 2.0. Next, by partial application, we build
a function computing the derivative of g at any point. Finally, we define a function
newton which searches the zero of a function. The newton function is also an higher
order function taking as argument the function for which a zero has to be found and its
derivative.
> let deriv f x h = ((f (x + h)) - (f x)) / h ;;
val deriv : (real{<expr>,<expr>,<expr>} -> real{’a,’b,’c})
-> real{<expr>,<expr>,<expr>} -> real{’d,’e,’f}
-> real{<expr>,<expr>,<expr>} = <fun>
> let g x = (x
*
x) - (5.0
*
x) + 6.0 ;;
val g : real{’a,’b,’c} -> real{<expr>,<expr>,<expr>} = <fun>
> deriv g 2.0 0.01 ;;
195
Numl - A Strongly Typed Language for Numerical Accuracy
195

- : real{
*
,5,51} = -0.9900000000000
> let gprime x = deriv g x 0.01 ;;
val gprime : real{<expr>,<expr>,<expr>} -> real{<expr>,<expr>,<expr>} = <fun>
> let rec newton x xold f fprime = if ((abs (x-xold))<0.01{
*
,10,20}) then x
else newton (x-((f x)/(fprime x))) x f fprime ;;
val newton : real{
*
,10,21} -> real{0,10,20} -> (real{
*
,10,21} -> real{’a,’b,’c})
-> (real{
*
,10,21} -> real{’d,’e,’f}) -> real{
*
,10,21} = <fun>
> newton 9.0 0.0 g gprime ;;
- : real{
*
,10,21} = 3.0001
We call the newton function with our function g and its derivative computed by
partial application of the deriv function. We obtain a root of our polynomial g with a
guaranteed accuracy. Note that while Newton-Raphson method converges quadratically
in the reals, numerical errors may perturb the process [6].
7 Case of the IEEE754 Floating-Point Arithmetic
In this section, we introduce modified versions of the types of primitives introduced in
Section 3.2. These modified versions are specific to the IEEE754 floating-point arith-
metic [1]. The types introduced in Figure 4 for the primitives corresponding to the ele-
mentary operations +, −, × and ÷ are not tailored for a specific arithmetic. They only
assume that the system has enough bits to perform the operations in the format given by
the types so that the results of the operations are not rounded. Numl interpreter fulfills
this requirement by performing all the numerical computations in multiple precision,
using the GNU Multiple Precision Arithmetic library GMP. Indeed, the type inference
enables to determine a priori the precision needed by GMP for the values and arithmetic
operations. An optimization would consists of also detecting when the computations fit
into hardware formats (generally the formats of the IEEE754 arithmetic introduced in
Figure 1) in order to avoid the calls to GMP when possible. The type information also
permits to generate code for the fixed-point arithmetic [12]. In this case, if the precision
of the formats corresponds to the types, no additional roundoff errors have to be added
and the general equations of Figure 4 hold again. In future work, we plan to develop a
compiler for our language (in addition to the current interpreter) which, based on the
formats given by the types, generates code using either the IEEE754 or the multiple
precision arithmetic (only when necessary). This compiler would also generate code
for the fixed-point arithmetic.
In practice, in many cases, one wants to use the IEEE754 floating-point arithmetic
and not multiple precision libraries, for efficiency reasons or because these library are
not available in certain contexts. In this case, the values and the results of the operations
do not necessarily fit inside the IEEE754 formats of Figure 1, they must be rounded. The
IEEE754 Standard defines five rounding modes for elementary operations over floating-
point numbers. These modes are towards −∞, towards +∞, towards zero, to the nearest
ties to even and to the nearest ties to away and we write them ◦
−∞
, ◦
+∞
, ◦
0
, ◦
∼
e
and
◦
∼
a
, respectively. The semantics of the elementary operations ∗ ∈ {+, −, ×, ÷} is
then defined by
f
1
∗
◦
f
2
= ◦ (f
1
∗ f
2
) (21)
196
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
196

% ∈ {11, 24, 53, 113}
P
%
+
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) =
(u
1
, u
2
) + σ
+
(s
1
, s
2
) − max


u
1
− p
1
,
u
2
− p
2
,
U
+
(s
1
, u
1
, s
2
, u
2
) − %


− ι
3


u
1
− p
1
,
u
2
− p
2
,
U
+
(s
1
, u
1
, s
2
, u
2
) − %


P
%
−
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) =
(u
1
, u
2
) + σ
−
(s
1
, s
2
) − max


u
1
− p
1
,
u
2
− p
2
,
U
−
(s
1
, u
1
, s
2
, u
2
) − %


− ι
3


u
1
− p
1
,
u
2
− p
2
,
U
−
(s
1
, u
1
, s
2
, u
2
) − %


P
%
×
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) =
u
1
+ u
2
+ 1 − max


u
1
+ u
2
+ 1 − p
1
,
u
1
− u
2
+ 1 − p
2
,
u
1
− u
2
+ 1 − %


− ι
3


u
1
+ u
2
+ 1 − p
1
,
u
1
− u
2
+ 1 − p
2
,
u
1
− u
2
+ 1 − %


P
%
÷
(s
1
, u
1
, p
1
, s
2
, u
2
, p
2
) = P
%
×
(u
1
, p
1
, u
2
, p
2
)
ι
3
(x, y, z) =

1 if x = y ∨ x = z ∨ y = z,
0 otherwise.
Fig. 11. Types of the IEEE754 floating-point arithmetic operators in precision %.
where ◦ ∈ {◦
−∞
, ◦
+∞
, ◦
0
, ◦
∼
e
, ◦
∼
a
} denotes the rounding mode. Equation (21) states
that the result of a floating-point operation ∗
◦
done with the rounding mode ◦ returns
what we would obtain by performing the exact operation ∗ and next rounding the result
using ◦. The IEEE754 Standard also specifies how the square root function must be
rounded in a similar way to Equation (21) but does not specify the roundoff of other
functions like sin, log, etc.
In the IEEE754 arithmetic, additional errors arise compared to the general context
of Section 3.2 and the types of the primitives of Figure 4 must be modified to correctly
model the errors of this specific arithmetic. The types of the IEEE754 primitives in
precision % ∈ {11, 24, 53, 113}, i.e. in half, single, double or quadruple precision, is
given in Figure 11. We assume that the rounding mode is ∼∈ {∼
a
, ∼
e
} (to the nearest.)
These equations model the fact that the accuracy of the result is dominated by either the
error on first operand or on the second operand or on the rounding of the result in
precision %. For example, the error on x +
∼
y is e
+
= ε(x) + ε(y) + ◦(x + y) with, by
Equation (21),
197
Numl - A Strongly Typed Language for Numerical Accuracy
197

◦(x + y) <
1
2
ulp(x + y) =
1
2
ufp(x + y) − % . (22)
The types of the other operators are obtained in a similar way to the addition. Let us
also note that in the IEEE754 floating-point arithmetic the constants may no longer be
in any precision. They must fit one of the formats given the standard.
8 Related Work
Several approaches have been proposed to determine the best floating-point formats
as a function of the expected accuracy on the results. Darulova and Kuncak use a for-
ward static analysis to compute the propagation of errors [8]. If the computed bound on
the accuracy satisfies the post-conditions then the analysis is run again with a smaller
format until the best format is found. Note that in this approach, all the values have the
same format (contrarily to our framework where each control-point has its own format).
While Darulova and Kuncak develop their own static analysis, other static techniques
[11, 24] could be used to infer from the forward error propagation the suitable formats.
Chiang et al. [5] have proposed a method to allocate a precision to the terms of an arith-
metic expression (only). They use a formal analysis via Symbolic Taylor Expansions
and error analysis based on interval functions. In spite of our linear constraints, they
solve a quadratically constrained quadratic program to obtain annotations.
Other approaches rely on dynamic analysis. For instance, the Precimonious tool
tries to decrease the precision of variables and checks whether the accuracy require-
ments are still fulfilled [19, 23]. Lam et al instrument binary codes in order to modify
their precision without modifying the source codes [14]. They also propose a dynamic
search method to identify the pieces of code where the precision should be modified.
Finally other work focus on formal methods and numerical analysis. A first related
research direction concerns formal proofs and the use of proof assistants to guaranty the
accuracy of finite-precision computations [3, 13, 15]. Another related research direction
concerns the compile-time optimization of programs in order to improve the accuracy
of the floating-point computation in function of given ranges for the inputs, without
modifying the formats of the numbers [7, 20].
9 Conclusion
In this article, we have introduced a dependent type system able to infer the accuracy
of numerical computations. Our type system allows one to type non-trivial programs
corresponding to implementations of classical numerical analysis methods. Unstable
computations are rejected by the type system. The consistency of typed programs is
ensured by a subject reduction theorem. To our knowledge, this is the first type system
dedicated to numerical accuracy. We believe that this approach has many advantages
going from early debugging to compiler optimizations. Indeed, we believe that the usual
type float proposed by usual ML implementations, and which is a simple clone of the
type int, is too poor for numerical computations. We also believe that this approach
is a credible alternative to static analysis techniques for numerical precision [8, 11, 24].
198
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
198

For the developer, our type system introduces few changes in the programming style,
limited to giving the accuracy of the inputs of the accuracy of comparisons to allow the
typing of certain recursive functions.
A first perspective to the present work is the implementation of a compiler for
Numl. We aim at using the type information to select the most appropriate formats
(the IEEE754 formats of Figure 1, multiple precisions numbers of the GMP library
when needed or requested by the user or fixed-point numbers.) In the longer term, we
also aim at introducing safe compile-time optimizations based on type preservation:
an expression may be safely (from the accuracy point of view) substituted to another
expression as long as both expressions are mathematically equivalent and that the new
expression has a greater type than the older one in the sense of Equation (6). Finally,
a second perspective is to integrate our type system into other applicative languages.
In particular, it would be of great interest to have such a type system inside a language
used to build critical embedded systems such as the synchronous language Lustre
[4]. In this context numerical accuracy requirements are strong and difficult to obtain.
Our type system could be integrated naturally inside Lustre or similar languages.
References
1. ANSI/IEEE: IEEE Standard for Binary Floating-point Arithmetic (2008)
2. Atkinson, K.: An Introduction to Numerical Analysis, 2nd Edition. Wiley (1989)
3. Boldo, S., Jourdan, J., Leroy, X., Melquiond, G.: Verified compilation of floating-point com-
putations. J. Autom. Reasoning 54(2), 135–163 (2015)
4. Caspi, P., Pilaud, D., Halbwachs, N., Plaice, J.: Lustre: A declarative language for program-
ming synchronous systems. In: POPL. pp. 178–188. ACM Press (1987)
5. Chiang, W., Baranowski, M., Briggs, I., Solovyev, A., Gopalakrishnan, G., Rakamaric, Z.:
Rigorous floating-point mixed-precision tuning. In: POPL. pp. 300–315. ACM (2017)
6. Damouche, N., Martel, M., Chapoutot, A.: Impact of accuracy optimization on the conver-
gence of numerical iterative methods. In: LOPSTR’15. LNCS, vol. LNCS 9527, pp. 1–18.
Springer (2015)
7. Damouche, N., Martel, M., Chapoutot, A.: Improving the numerical accuracy of programs
by automatic transformation. STTT 19(4), 427–448 (2017)
8. Darulova, E., Kuncak, V.: Sound compilation of reals. In: POPL’14. pp. 235–248. ACM
(2014)
9. Denis, C., de Oliveira Castro, P., Petit, E.: Verificarlo: Checking floating point accuracy
through monte carlo arithmetic. In: ARITH’16. pp. 55–62. IEEE (2016)
10. Franco, A.D., Guo, H., Rubio-Gonz
´
alez, C.: A comprehensive study of real-world numerical
bug characteristics. In: ASE. pp. 509–519. IEEE (2017)
11. Goubault, E.: Static analysis by abstract interpretation of numerical programs and systems,
and FLUCTUAT. In: SAS. LNCS, vol. 7935, pp. 1–3. Springer (2013)
12. Graphics, M.: Algorithmic C Datatypes, software version 2.6 edn. (2011), http://www.
mentor.com/esl/catapult/algorithmic
13. Harrison, J.: Floating-point verification. J. UCS 13(5), 629–638 (2007)
14. Lam, M.O., Hollingsworth, J.K., de Supinski, B.R., LeGendre, M.P.: Automatically adapting
programs for mixed-precision floating-point computation. In: Supercomputing, ICS’13. pp.
369–378. ACM (2013)
15. Lee, W., Sharma, R., Aiken, A.: On automatically proving the correctness of math.h imple-
mentations. PACMPL 2(POPL), 47:1–47:32 (2018)
199
Numl - A Strongly Typed Language for Numerical Accuracy
199

16. Martel, M.: Floating-point format inference in mixed-precision. In: NFM. LNCS, vol. 10227,
pp. 230–246 (2017)
17. Milner, R., Harper, R., MacQueen, D., Tofte, M.: The Definition of Standard ML. MIT Press
(1997)
18. de Moura, L.M., Bjørner, N.: Z3: an efficient SMT solver. In: TACAS. LNCS, vol. 4963, pp.
337–340. Springer (2008)
19. Nguyen, C., Rubio-Gonzalez, C., Mehne, B., Sen, K., Demmel, J., Kahan, W., Iancu, C.,
Lavrijsen, W., Bailey, D.H., Hough, D.: Floating-point precision tuning using blame analysis.
In: ICSE. ACM (2016)
20. Panchekha, P., Sanchez-Stern, A., Wilcox, J.R., Tatlock, Z.: Automatically improving accu-
racy for floating point expressions. In: PLDI. pp. 1–11. ACM (2015)
21. Pierce, B.C.: Types and programming languages. MIT Press (2002)
22. Pierce, B.C. (ed.): Advanced Topics in Types and Programming Languages. MIT Press
(2004)
23. Rubio-Gonzalez, C., Nguyen, C., Nguyen, H.D., Demmel, J., Kahan, W., Sen, K., Bailey,
D.H., Iancu, C., Hough, D.: Precimonious: tuning assistant for floating-point precision. In:
HPCNSA. pp. 27:1–27:12. ACM (2013)
24. Solovyev, A., Jacobsen, C., Rakamaric, Z., Gopalakrishnan, G.: Rigorous estimation of
floating-point round-off errors with symbolic taylor expansions. In: FM. LNCS, vol. 9109,
pp. 532–550. Springer (2015)
200
EPS Portugal 2017/2018 2017 - OPPORTUNITIES AND CHALLENGES for European Projects
200