Advancements of Methods for Fast and Accurate Estimation of

Human Body Segment Parameter Values

Pelin Cizgin

, Philipp Kornfeind

, Michaela Haßmann

and Arnold Baca

Institute of Molecular Biotechnology, Vienna, Austria

Department of Biomechanics/Kinesiology and Computer Science in Sport, University of Vienna, Vienna, Austria

Keywords: Geometric Models, Anthropometry, Inverse Dynamics, Human Motion Analysis.

Abstract: In order to assess joint loads and to estimate joint reaction forces and net joint torques in human motion

analysis, inverse dynamic approaches are commonly applied. These approaches rely on an accurate estimation

of human body segment parameter values. The paper gives an overview of contemporary methods with a

specific focus on approaches based on geometrical models, where image based or photogrammetric

techniques are applied for estimating the parameter values fast and accurately.

1 INTRODUCTION

For the understanding of the cause of any movement

the knowledge of patterns of forces acting on and

within the human body is required. In general, forces

are calculated indirectly using kinematic, kinetic and

anthropometric data. A full kinematic description,

accurate anthropometric measures, and external

forces, are used to calculate joint reaction forces and

net joint torques. This prediction is called an inverse

solution and is a very powerful tool in motion analysis

(Winter, 2005). Accurate estimations of human body

segment parameter values (BSPs) are required to

obtain accurate inverse solutions. These parameters

comprise volume, mass, location of center of mass,

principal moments of inertia and location of the

principal axes of inertia. Studies (for example, Rao

(2006)) have shown the sensitivity of inverse

dynamic solutions to BSP.

2 AN OVERVIEW OF METHODS

Different approaches have been followed in order to

determine human body segment parameter values. In

the sequel, we will differentiate between statistical

methods, methods based on medical imaging

technologies, such as computerized-tomography

(CT) or magnetic resonance imaging (MRI), methods

based on geometrical models and dynamic parameter

estimation methods.

2.1 Statistical Methods

Popular sources for BSP information are regression

equations generated from human cadaver data

(Dempster, 1955); (Clauser et al., 1969); (Drillis and

Contini, 1966), which incorporate whole body and/or

segment anthropometric measurements to predict

BSPs. These equations provide quick and easy

methods for human BSPs estimation, but have been

criticized in several ways. An obvious problem of

cadaver-based prediction is that they typically are

based on data from a limited number of elderly

cadavers, which may result in limited accuracy (cf.

Nigg and Herzog (1999)). Erdmann and Kowalczyk

(2015) propose a method for estimating volume, mass

and location of center of mass of body segments

based on regression equations developed by Erdmann

(1997) using data from CT scans and Clauser et al.,

(1969). They put particular attention to the trunk,

which is, according to Erdmann’s (1997) method

divided into subparts consisting of tissues of different

density.

2.2 Methods based on Medical Imaging

Technologies

Living-based, predictive models for BSP estimation

involve the use of gamma ray scanning (Zatsiorsky,

et al., 1990), CT (Ackland et al., 1988), MRI (Cheng

et al., 2000), dual energy X-ray (Durkin et al., 2002),

and combinations of methods. The approach of

Cizgin P., Kornfeind P., HaÃ§mann M. and Baca A.

Advancements of Methods for Fast and Accurate Estimation of Human Body Segment Parameter Values.

DOI: 10.5220/0006439400690074

In Proceedings of the 5th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2017), pages 69-74

ISBN: 978-989-758-269-1

Durkin et al., (2002), for example, makes use of two

X-ray intensities in order to determine bone material

and soft tissue masses separately. Even though all

these methods provide accurate BSPs estimations on

living subjects, especially CT imaging and gamma-

mass scanning, as well as X-ray methods underlie

criticism because of the high costs and the radiation

which the subjects are exposed to (cf. (Rossi et al.,

2013).

2.3 Methods based on Geometrical

Models

Geometrical models are based on geometric figure

templates for segments. The exact shapes are defined

by a certain number of anthropometric measurements.

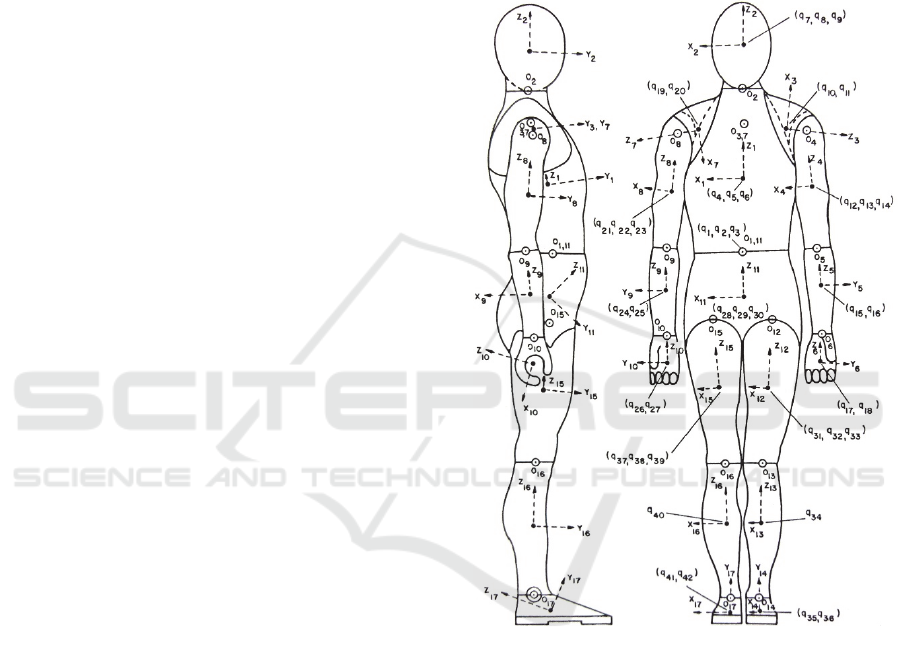
A popular model is that proposed by Hanavan (1964).

25 anthropometric dimensions are required for

defining the shapes of all body segments. Another

well-known and, to our knowledge, most accurate

mathematical model for the computational estimation

of BSP is the one published by Hatze (1979; 1980).

The model (“hominoid”) is based on 242

anthropometric input values. Hatze’s model

combines a volume and density function to estimate

segment inertial parameters. Segments are sectioned

into more than one shape, from which the volume can

be estimated, to get more detail in contours of a body

segment. In addition, this is coupled with a non-

uniform density function. The hominoid model (see

Fig.1) accounts for exomorphic and tissue density

differences between males and females, segmental

shape fluctuations and asymmetries in geometries of

segments. There is, however, a high expenditure for

the manual determination of the required input

values. The direct measurement of the 242

anthropometric dimensions takes about 60-80

minutes.

2.4 Dynamic Parameter Estimation

Methods

Methods of that kind are characterized by parameter

fitting approaches based on kinematics and measured

external forces.

We are aware of three notable developments,

which have been published recently. Díaz-Rodríguez

et al., (2016) apply a robotics formalism. They first

estimate mass and center of gravity from a static

model and include the results in a dynamic model in

order to estimate the moment of inertia. Bonnet et al.,

(2016) identify the mass, center of gravity and

moments of inertia over a number of static and

dynamic postures using optimal exciting motions.

Son et al., (2014) suggest a method based on the

dynamic equation of motion. They perform

consecutive steps using a commercial dynamometer.

First, a quasi-static passive movement is executed,

next a fast movement of the segment under

investigation with and without addition of an

attachment and finally of just the attachment. In both

studies, however, inertial parameters have only been

determined for selected segments.

Figure 1: Hominoid. Adapted from (Hatze, 1983).

3 TOWARDS FAST

AVAILABILITY OF SEGMENT

PARAMETER VALUES

There is little debate that a geometric model with a

non-uniform density function provides a very

accurate BSP estimation. However, especially for

clinical analyses of gait and posture non-invasive,

safe, cost-effective and, in particular, rapid methods

are from high importance in addition to providing

accurate parameter values.

Image based or photogrammetric approaches

provide means for capturing shape related data and

the required geometric outlines without much effort.

Clarkson et al., (2012) introduced a method based on

a Microsoft Kinect based sensor system, whereas

Peyer et al., (2015); Sheets et al., (2010) as well as Lu

and Wang (2008) applied 3D body scanners.

Figure 2: Video image for determination of anthropometric

dimensions of hominoid model (cf. (Baca, 1996)).

3.1 A Video-based Approach for the

Hominoid

In 1996, Baca introduced a method for determining

the anthropometric data required for Hatze’s

hominoid (Baca, 1996). This method is accurate, but

still somewhat time consuming, because several

images from different planes have to be recorded. An

example of one of the four recordings required is

given in Fig. 2.

3.2 Application of 3D Scanners

The development of 3D scanners in the past decade

has attracted several fields of science. Automated

whole body scanner technology merged on the market

offering the possibility of obtaining three-dimen-

sional coordinates of measuring points on the surface

of the object of interest fast, accurate and reliable.

By combining scanner based measurements and

accurate mathematical segment models considering

non-uniform density distributions both fast and

accurate estimation of body segment parameters may

be provided. The applicability of three-dimensional

body scanning technology (Vitus Smart XXL,

Vitronic, Wiesbaden, Germany) for determining

automated or semi-automated individual

anthropometric dimensions of Hatze’s hominoid in

order to determine subject specific body segment

parameter values has therefore been investigated in

the working group of the last author of this paper. The

3D body scanner used allows capturing full body

scans with an accuracy of ± 1 mm. An example of a

3D-scan is shown in Fig. 3.

Figure 3: 3D-scan from Vitus Smart XXL 3D body scanner.

3.2.1 Automated Segmentation

The master thesis of Schiffl (2011) investigated the

utility of the 3D scanner for the automatic

segmentation of scan data into the 17 segments of

Hatze’s anthropomorphic model. Comparatively

large differences were observed for the segment

lengths and volumes (e..g. more than 20 % for the

volume of the abdomino-thoracic segment) when

determined as well manually as by applying the

automated method.

3.2.2 A Semi-automated Approach

In order to overcome this problem, a semi-automated

approach was followed in the master thesis of Cizgin

(2013). The overall procedure for estimating all

segment parameter values, which in total takes about

10-12 minutes, is as follows: First, the subject is

prepared (clothing, bathing cap, 5 markers). Then, the

subject is scanned in two different body postures.

Whole body scans captured by Vitus Smart XXL,

Vitronic 3D Body Scanner provide surface images as

point clouds into the ScanWorX Software Solution

(Kaiserslautern, Germany). The measurement

module AnthroScan detects nearly all necessary

landmark points relevant to Hatze’s geometrical

model automatically. The five landmarks which

cannot be recognized accurately by the software

(right jaw joint, most protruding point of left and right

scapula, left and right hip joint center) have to be

localized physically on the subject and marked with

small circular markers before the scanning process.

Once the surface image is visible as a 3D point cloud

in the application, the user can position the relevant

landmarks on the screen precisely guided through

step by step introduction. Finally, the measurements,

which should be performed disregarding

subcutaneous fat in abdominal-pelvic section must be

performed by direct measuring method. Because of

this combination of automated calculation and user

based positioning of icons, this approach is

considered as a semi-automated determination.

Furthermore, the application does not require any

surface mesh procedures. The captured surface cloud

point image is in sufficient detail and almost gap free

reconstructed. By extending the implementation of

the application, all Hatze relevant 242 subject specific

anthropometric measurements can be automatically

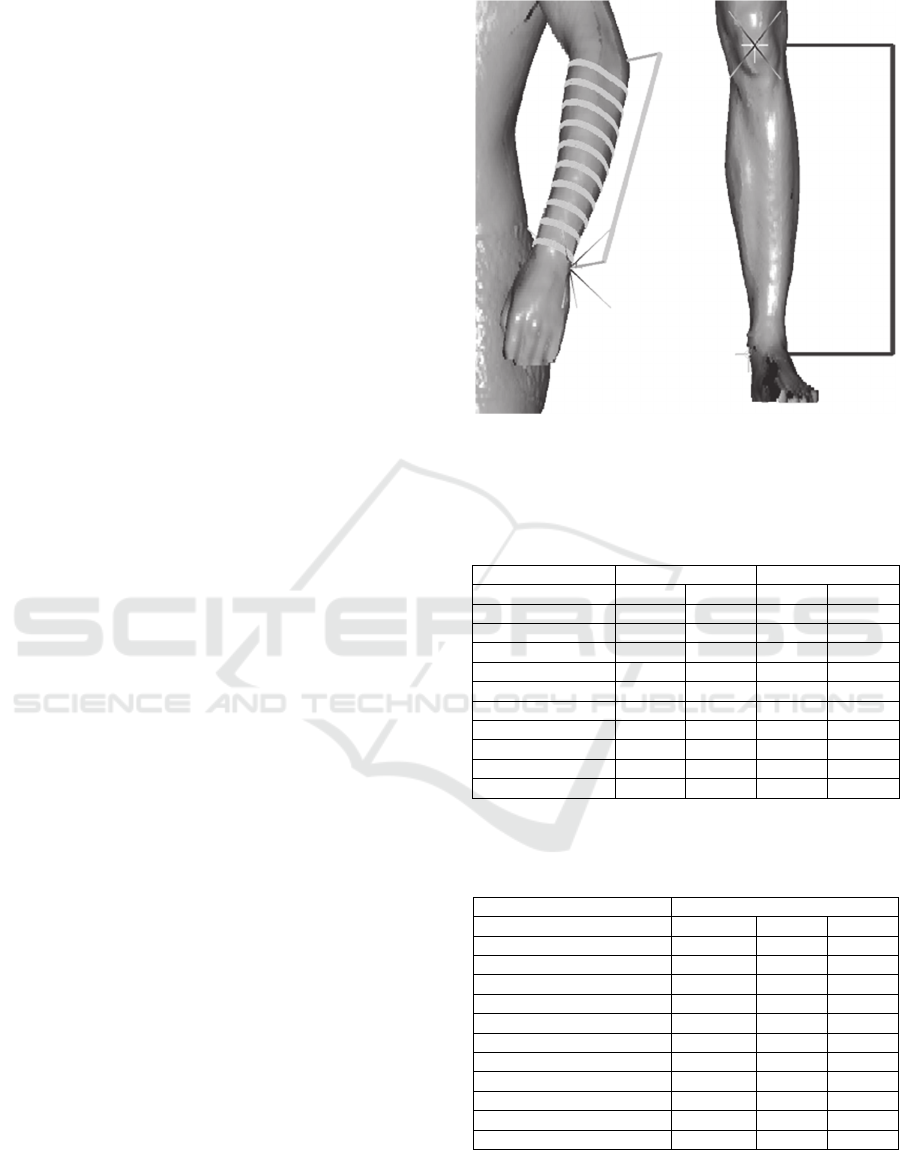
determined. Fig. 4 shown as an example represents

the visualization of the virtual tape for taking the

perimeters and length measures of the underarm and

leg within the 3D scan image.

Mean absolute and/or relative differences (6

subjects) between the manual and the semi-automated

approach for determining parameter values of

selected segments are presented in Tab. 1. and Tab. 2.

Both, negative and positive differences were found

when comparing approaches. Deviations of more than

10 % were only observed in principal moments of

inertia of small segments, which typically have

limited influence on the result of analyses of whole-

body motions.

The semi-automatic approach has shown to be

suited for estimating human segment parameter

values fast and accurate. The overall duration for one

subject is about 12 to 15 minutes, whereas 60 to 80

minutes were required for the procedure based on

manual measurements. A general drawback of

methods based on the particular 3D scanner used lies

in the comparatively high costs of the scanning

device. It should, however, be possible substituting

this specific instrument by scanners demanding lower

costs (for example as described in Peyer et al., (2015),

given that a similar scan resolution may be obtained.

Figure 4: Virtual tape for taking perimeters and length

measures.

Table 1: Mean relative and absolute differences (n=6)

between length and mass obtained using manual

measurement and semi-automated approach.

length mass

segment [%] [mm] [%] [kg]

abdomino-thoracic 1,2 5,7 4,7 0,751

head neck 1,0 2,2 1,8 0,105

left shoulder 2,5 3,0 6,4 0,059

left (upper) arm 2,2 6,0 4,1 0,081

left forearm 2,4 6,3 4,2 0,054

left hand 2,6 2,2 7,6 0,023

abdomino-pelvic 1,9 4,8 2,1 0,302

left thigh 2,5 7,7 2,3 0,173

left leg 1,4 5,8 2,2 0,076

left foot 2,1 4,7 5,6 0,042

Table 2: Mean relative differences (n=6) between principal

moments of inertia obtained using manual measurement

and semi-automated approach.

principal moments of inertia

x y z

segment [%] [%] [%]

abdomino-thoracic 7,3 7,6 5,9

head neck 3,7 2,9 3,1

left shoulder 6,1 18,1 10,3

left (upper) arm 8,8 9,1 5,1

left forearm 7,2 7,1 7,9

left hand 10,8 21,0 17,7

abdomino-pelvic 7,3 4,1 6,9

left thigh 4,0 3,8 4,6

left leg 4,6 4,8 3,7

left foot 3,5 3,3 11,3

4 CONCLUSION

Geometric segment models combined with a non-

uniform density function enable a very accurate BSP

estimation. If anthropometric dimensions defining the

shapes of these models are determined using three-

dimensional body scanning technology, the overall

parameter estimation process can be performed in

some minutes. The semi-automated approach as

described decreases time for data collection, whilst

maintaining body segment accuracy when compared

to the manual method.

REFERENCES

Ackland, T., Henson, P., Bailey, D., 1988. The uniform

density assumption: Its effect upon the estimation of

body segment inertial parameters. International

Journal of Sports Biomechanics, 4, 146-155.

Baca, A., 1996. Precise determination of anthropometric

dimensions by means of image processing methods for

estimating human body segment parameter values.

Journal of Biomechanics, 29(4), 563-567.

Cheng, C.-K., Chen, H.-H., Chen, C.-S., Lee, C.-L., Chen,

C.-Y, 2000. Segment inertial properties of Chinese

adults determined from magnetic resonance imaging.

Clinical Biomechanics, 15(8), 559-566.

Cizgin, P., 2013. Automatisierte Bestimmung

anthropometrischer Segmentparameter des

Hominoidmodells von Hatze mittels 3D-

Laserscantechnologie. Master thesis, Medical

University Vienna, 2013.

Clarkson, S., Choppin, S., Hart, J., Heller, B., Wheat, J.,

2012. Calculating body segment inertia parameters

from a single rapid scan using the Microsoft Kinect. In

Proc 3

International Conference on 3D Body

Scanning Technologies, Lugano, Switzerland, 16.-17

October 2012.

Clauser, C. E., McConville, J. T., Young, J. W., 1969.

Weight, volume and center of mass of segments of the

human body. AMRL Technical. Report, Wright-

Patterson Air Force Base, Ohio.

Crosnier, P., Gautier, M., Gonzáles, A., Venture, G., 2016.

Optimal Exciting Dance for Identifying Inertial

Parameters of an Anthropomorphic Structure. IEEE

Transactions on Robotics, 32(4), 823-836.

Dempster, W.T., 1955. Space requirements for the seated

operator. Wright Air Development Center. Wright-

Patterson Air Force Base, Dayton, OH, WADC Tech.

Rep. TR-55-159.

Díaz-Rodríguez, M., Valera, A., Page, A., Besa, A., Mata,

V., 2016. Dynamic Parameter Identification of Subject-

Specific Body Segment Parameters Using Robotics

Formalism: Case Study Head Complex. ASME.

Journal of Biomechanical Engineering,

138(5):051009-051009-8.doi:10.1115/1.4032997.

Drillis, R., Contini, R., 1966. Body Segment Parameters.

New York, New York: Office of Vocational

Rehabilitation, Report No.: No. 1166-03.

Durkin, J. L., Dowling, J. J., Andrews D. M., 2002. The

measurement of body segment inertial parameters using

dual energy X-ray absorptiometry. Journal of

Biomechanics, 35(12), 1575-1580.

Erdmann, W. S., 1997. Geometric and inertial data of the

trunk in adult males. Journal of Biomechanics, 30(7),

679-688.

Erdmann, W. S., Kowalczyk, R., 2015. A personalized

method for estimating centre of mass location of the

whole body based on differentiation of tissues of a

multi-divided trunk. Journal of Biomechanics, 48(1),

65-72.

Hanavan, Jr., E. P., 1964. A mathematical model of the

human body (No. AFIT-GA-PHYS-64-3). Air Force

Aerospace Medical Research Lab Wright-Patterson

Afb Oh.

Hatze, H., 1979. A model for the computational

determination of parameter values of anthropomorphic

segments. CSIR Techn. Report TWISK 79, Pretoria.

Hatze, H., 1980. A mathematical model for the

computational determination of parameter values of

anthropomorphic segments. Journal of Biomechanics,

13 (10), 833-843.

Hatze, H., 1983. Computerized optimization of sports

motions: an overview of possibilities, methods and

recent developments. Journal of Sports Science, 1, 3-

12.

Lu, J.-M., Wang, M.-J. J., 2008. Automated anthropometric

data collection using 3D whole body scanners, Expert

Systems with Applications, 35, 407-414.

Nigg, B. M., Herzog, W. (Eds.), 1999. Biomechanics of the

muskulo-skeletal system. 2nd Edition. Chichester: John

Wiley & Sons.

Peyer, K. E., Morris, M., Sellers, W. I., 2015. Subject-

specific body segment parameter estimation using 3D

photogrammetry with multiple cameras,

PeerJ:e381,DOI 10.7717/peerj.831.

Rao, G., Amarantini, D., Berton, E., Favier, D., 2006.

Influence of body segments’ parameters estimation

models on inverse dynamics solutions during gait,

Journal of Biomechanics, 39 (8), 1531-1536.

Rossi, M., Lyttle, A., El-Sallam, A., Benjanuvatra, N.,

Blanksby, B., 2013. Body segment inertial parameters

of elite swimmers using DXA and indirect methods.

Journal of Sports Science and Medicine, 12(4), 761-

775.

Schiffl, K., 2011. Bestimmung von Hominoidsegmenten aus

3D-Bodyscannerdaten. Master thesis, Technical

University Vienna, 2011.

Sheets, A.L., Corazza, S., Andriacchi, T. P., 2010. An

automated image-based method of 3D subject-specific

body segment parameter estimation for kinetic analyses

of rapid movements. Journal of Biomechanical

Engineering, 132 (1), 011004.

Son, J., Ryu, J., Kim, J., Kim, Y., 2014. Determination of

inertial parameters using a dynamometer. Bio-Medical

Materials and Engineering 24, 2447-2455.

Winter, D., 2005. Biomechanics and motor control of

human movement. New Jersey: John Wiley & Sons Inc.

Zatsiorsky, V., Seluyanov, V., Chugunova, L., 1990. In

vivo body segment inertial parameter determination

using a gamma-scanner method. In Biomechanics of

Human Movement: Applications in Rehabilitation,

Sports and Ergonomics. Eds: Berme, N. and Cappozzo,

A. Bertec, Ohio. 186-202.