First Practical Side-channel Attack to Defeat Point Randomization in
Secure Implementations of Pairing-based Cryptography
Damien Jauvart
1,2
, Jacques J. A. Fournier
3
and Louis Goubin
2
1
CEA Tech, Centre Micro
´
electronique de Provence, 880 avenue de Mimet, 13541 Gardanne, France
2
Laboratoire de Math
´
ematiques de Versailles, UVSQ, CNRS, Universit
´
e Paris-Saclay, 78035 Versailles, France
3
CEA LETI, 17 rue des Martyrs, 38054 Grenoble Cedex 9, France
Keywords:
Pairing-based Cryptography, Miller’s Algorithm, Collision Side-channel Attack, Countermeasures.
Abstract:
The field of Pairing Based Cryptography (PBC) has seen recent advances in the simplification of their cal-
culations and in the implementation of original protocols for security and privacy. Like most cryptographic
algorithms, PBC implementations on embedded devices are exposed to physical attacks such as side channel
attacks, which have been shown to recover the secret points used in some PBC-based schemes. Various coun-
termeasures have consequently been proposed. The present paper provides an updated review of the state of
the art countermeasures against side channel attacks that target PBC implementations. We especially focus on
a technique based on point blinding/randomization. We propose a collision based side-channel attack against
an implementation embedding the point randomization countermeasure. It is, to the best of our knowledge,
the first proposed attack against this countermeasure used in the PBC context and this raises questions about
the validation of countermeasures for complex cryptographic schemes such as PBC. We also discuss about
ways of thwarting our attack.
1 INTRODUCTION
Bilinear pairings are used in cryptography for various
innovative protocols. For example, in 2001, Boneh
and Franklin published the Identity-Based Encryption
(IBE) scheme based on Pairings (Boneh and Franklin,
2001). The one-round tripartite key exchange (Joux,
2004) based on Pairings is another interesting practi-
cal use of such cryptographic primitives.
Several studies have investigated about the vul-
nerability of Pairing-Based Cryptography (PBC) to
side-channel attacks. The first papers to consider
the security of pairings regarding side-channel at-
tacks were mainly concerned with elliptic curves de-
fined over small fields of characteristics 2 and 3. Al-
though Joux (Joux et al., 2014) and Barbulescu (Bar-
bulescu et al., 2015a) recently suggested that such
fields should be avoided, some of those techniques in-
tended for small characteristic fields can nevertheless
be applied over large prime fields.
In an IBE (Boneh and Franklin, 2001) scheme that
uses pairings, a cipher is decrypted by the computa-
tion of a pairing between a secret point and another
point that is part of the input cipher. In a nutshell,
in the IBE (Boneh and Franklin, 2001) scheme the
decryption step consists in deciphering the ciphertext
{U,V } with U ∈ G
1
and V ∈ {0,1}
n
using the pri-
vate key D. The entity needs to compute e(D,U).
Side-channel attacks against such a scenario aim at
exploiting the interaction between the known cipher-
text and the secret point (which is part of the private
secret key). A pairing calculation has a double-and-
add structure, as is the case in Elliptic Curve Cryp-
tography (ECC). However, with PBC the problem re-
garding side-channel attacks is different: the num-
ber of iterations and the scalar are known, and the
secret is one of the arguments of the pairing. Con-
sequently, side-channel attacks on PBC implementa-
tions are more likely to rely on CPA
1
-like techniques
to target the secret point (compared to using SPA
2
-
like approaches to target the scalar in the double-and-
add structure).
In this paper, we review various side-channel at-
tacks used against PBC implementations and the as-
sociated countermeasures. We then focus on one of
those countermeasures and explain and illustrate how
to defeat it. The paper is organized as follows. Sec-
1
Correlation Power Analysis
2
Simple Power Analysis
104
Jauvart, D., Fournier, J. and Goubin, L.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography.
DOI: 10.5220/0006425501040115
In Proceedings of the 14th International Joint Conference on e-Business and Telecommunications (ICETE 2017) - Volume 4: SECRYPT, pages 104-115
ISBN: 978-989-758-259-2
Copyright © 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

τ
l
: E (F
q
)[l] ×E (F
q
) →
F
?
q
k
/

F
?
q
k

l
→ µ
l
⊂ F
?
q
k
P,Q 7→ f
P
(Q) 7→ f
P
(Q)
q
k
−1
l
. (2)
tion 2 recalls the basic definitions of and notations for
pairings. We review related work in Section 3. Sec-
tion 4 provides an analysis of one of those counter-
measures which is based on point randomization and
explains how this countermeasure can be defeated.
Then section 5 describes the practical experiments
and results obtained when implementing this attack
against a software Pairing calculation running on a
32-bit platform. A conclusion is then proposed in
Section 6.
2 PAIRINGS AS A
CRYPTOGRAPHIC
APPLICATION
In this section, we provide the concepts and notations
that will be used throughout this paper. For a detailed
explanation of pairings we refer the reader to (Silver-
man, 2009).
Let G
1
and G
2
be two abelian groups and G
3
a
multiplicative group of the same order. A pairing is a
map e : G
1
×G
2
→ G
3
with the following properties:
1. Non-degeneracy: ∀P ∈ G
1
\{O} ∃Q ∈ G
2
such
that e(P,Q) 6= 1,
2. Bilinearity:
e([a]P
1
+ [b]P
2
,Q) = e(P
1
,Q)
a
e(P
2
,Q)
b
e(P,[a]Q
1
+ [b]Q
2
) = e(P,Q
1
)
a
e(P,Q
2
)
b
.
The above properties can be verified by using
groups of points on elliptic curves for both abelian
groups.
Let E be an elliptic curve defined over F
q
. E can
be written as
E = {(x,y) ∈ F
q
×F
q
|y
2
+ a
1
xy + a
3
y
= x
3
+ a
2
x
2
+ a
4
x + a
6
}∪{O},
(1)
where O denotes the point at infinity: it is the iden-
tity element for the addition group law. The set of
l-torsion points of E is E[l] := ker[l] (the set of points
P in E such that [l]P = O), the rational torsion points
are given by E (F
q
)[l] := E (F
q
) ∩E[l]. The group
E (F
q
)[l] contains a point of order l, the smallest pos-
itive integer k such that l divides q
k
−1 is called the
embedding degree of E (F
q
) with respect to l.
The Tate Pairing. The widely used Tate pair-
ing (Barreto et al., 2002; Eisentr
¨
ager et al., 2004; Gal-
braith et al., 2002; Scott, 2005) takes as inputs two
points P and Q such that P ∈E (F
q
)[l] and Q ∈E (F
q
)
as provided in Equation 2 where µ
l
is the group of the
l-th roots of unity such that µ
l
= {ξ ∈ F
?
q
k
|ξ
l
= 1}.
A final exponentiation
q
k
−1
l
is applied to the output
f
P
(Q) in order to obtain a unique value of order l.
The Barreto–Naehrig Curves (Barreto and
Naehrig, 2005). Such curves are widely used
to get efficient implementations of pairings. The
pairing-friendly ordinary elliptic curves over a prime
field F
q
are defined by E : y
2
= x
3
+ b where b 6= 0.
Their embedding degree is k = 12. The order of E is
l, a prime number. The BN curves are parametrized
with p and l as follows:
p(t) = 36t
4
+ 36t
3
+ 24t
2
+ 6t +1,
l(t) = 36t
4
+ 36t
3
+ 18t
2
+ 6t +1,
(3)
where t ∈ Z is chosen in order to get p(t) coprime to
l(t) and large enough to guarantee an adequate secu-
rity level.
Miller’s Algorithm. The computation of such a
map is a well known problem (Barreto et al., 2002)
and an efficient way of computing such pairings was
proposed as a recursive scheme by Miller (Miller,
1986). Miller’s algorithm, which works as the main
calculation to compute a pairing, uses an iterative re-
lation to find a rational function f
P
. The Miller’s loop
is given in Algorithm 1.
In Algorithm 1:
1. l
T,T
(Q) is the equation of the tangent at T evalu-
ated at point Q.
2. l
T,P
(Q) is the equation of the line through T and
P evaluated at point Q.
3. v
R
(Q) is the equation of the vertical line at R eval-
uated at Q.
These equations can be optimized by using mixed sys-
tem coordinates for the points’ representations as sug-
gested in (Aranha et al., 2011; Bajard and El Mra-
bet, 2007; Beuchat et al., 2010; Koblitz and Menezes,
2005) and (Naehrig et al., 2010):
1. P and Q are in affine coordinates.
2. T is in Jacobian coordinates, i.e. if T = (x
T
,y
T
) =

X
T
Z
2
T
,
Y
T
Z
3
T

in affine coordinates then T = (X
T
: Y
T
:
Z
T
) in Jacobian.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
105

Algorithm 1: Miller’s algorithm.
Data: l = (l
n−1
...l
0
)
2
, P ∈ G
1
and Q ∈ G
2
Result: f
P
(Q) ∈ G
3
1 T ← P;
2 f ←1;
3 for i = n −1 downto 0 do
4 f ← f
2
l
T,T
(Q)
v
[2]T
(Q)
;
5 T ← [2]T ;
6 if l
i
== 1 then
7 f ← f
l
T,P
(Q)
v
T +P
(Q)
;
8 T ← T + P;
9 end
10 end
11 return f ;
With this representation the tangent and line equa-
tion are shown in Equation 4. These equations are
presented without their denominator because they are
elements of a strict subfield of F
q
k
and therefore the fi-
nal exponentiation sends these elements to 1 (the neu-
tral element for multiplication).
In the following, our implementation is a Tate
pairing over Barreto and Naehrig curves (Barreto and
Naehrig, 2005).
2.1 Application to Identity-based
Encryption
An IBE scheme can be used to simplify a widely
known issue in public key cryptography: the key ex-
change. A Public-Key Infrastructure (PKI) based on
IBE is less complex and more scalable compared to
classical schemes (with certifications).
In an IBE, the public key of a character is its iden-
tity. The associated private key can’t be computed
by this character, but generated by the le Private Key
Generator (PKG). Of course, the decryption should be
possible only with the private key.
A simplified version of the scheme of Boneh-
Franklin (Boneh and Franklin, 2001) work in four
steps: 1. Set-up; 2. Extraction; 3. Encryption; 4.
Decryption.
Setup. The PKG have to generate some public pa-
rameters for the pairings. Let G
1
and G
2
be two
groups of order l such that e : G
1
×G
1
→ G
2
is a
bilinear pairing. Let P ∈ G
1
be a generator of G
1
.
let H
1
: {0,1}
?
→ G
?
1
and H
2
: G
2
→ {0,1}
n
be two
cryptographic hash functions. Let s ∈Z
r
be a random
is their private key (a master key of the system). Let
P
PU B
= [s]P be the global public key. The set of public
parameters is
{r, n, G
1
,G
2
,e,P, P
PU B
,H
1
,H
2
}.
Extraction. The extraction algorithm supplies the
private key of a user. Let ID = ”Bob” ∈ {0,1}
?
be
the identity of a user Bob. The PKG hashes this string
onto G
1
to obtain Q
B
= H
1
(ID). Bob’s private key is
d
B
= [s]Q
B
(computed and transmitted to Bob by the
PKG).
Encryption. Alice wants to send a message M ∈
{0,1}
n
to Bob, she proceeds as follows:
1. She computes Q
B
= H
1
(”Bob”).
2. She randomly picks k.
3. She computes g
B
= e(Q
B
,P
PU B
) ∈ G
?
2
.
4. And, she computes the ciphertext C = {[k]P,M ⊕
H
2
(g
k
B
)} and sends it to Bob.
Decryption. Bob wants to decrypt the ciphertext
C = {U,V } where U ∈ G
1
,V ∈ {0,1}
n
, he proceeds
as follows:
1. He computes e(d
B
,U) which is equal to
e([s]Q
B
,[k]P) = e(Q
B
,P)
sk
= e(Q
B
,[s]P)
k
=
e(Q
B
,P
PU B
)
k
= g
k
B
.
2. He gets the message M = V ⊕H
2
(g
k
B
).
3 RELATED WORK AND
CONTRIBUTIONS
Differential Power Analysis (DPA) attacks have been
first introduced by Kocher et al. in (Kocher et al.,
1999). Since then, DPA-like techniques have been
successfully used to attack implementations of most
cryptographic algorithms.
3.1 Related Work in Side-channel
Attacks Against Pairings
The first paper to investigate about the physical se-
curity of pairing algorithms was published in 2004.
In this paper, Page and Vercauteren (Page and Ver-
cauteren, 2004) simulated an attack on the Duursma–
Lee Algorithm (Duursma and Lee, 2003) which is
used to compute Tate pairings using elliptic curves
over finite fields of characteristic 3. The authors ex-
posed the vulnerability of such pairings with respect
to active (fault injections) and passive (side-channel
observations) attacks. The authors also proposed two
countermeasures to thwart side channel attacks.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
106

l
T,T
(Q) = 2y
Q
Y
T
Z
3
T
−2Y
2
T
−

3X
2
T
+ aZ
4
T

x
Q
Z
2
T
−X
T

l
T,P
(Q) = (y
Q
−y
P
)Z
T

X
T
−Z
2
T
x
P

−

Y
T
−Z
3
T
y
P

(x
Q
−x
P
)
(4)
The first countermeasure is based on the bilin-
earity of the pairing where, if a and b are two ran-
dom values, with e([a]P,[b]Q)
1
/ab
= e(P,Q), then for
each pairing computation, we take different values for
a and b, and compute e([a]P,[b]Q)
1
/ab
. The second
countermeasure, proposed in (Page and Vercauteren,
2004), works for cases where P is secret and a mask is
added to the point Q as follows: select a random point
R ∈ G
2
and compute e(P,Q + R)e(P,R)
−1
instead of
e(P,Q), with different random values of R at every
call to e.
The main inconvenience of these countermeasures
is the computation overhead where two pairings are
calculated instead of one.
Pan and Marnane (Pan and Marnane, 2011) sim-
ulated a side-channel attack where they proposed a
CPA based on a Hamming distance model to target a
pairing over a base field of characteristic 2 over super-
singular curves. The practical results obtained by Pan
and Marnane can be used to assess the feasibility of
using CPA to target pairings on an FPGA platform.
Kim et al. (Kim et al., 2006) also examined the se-
curity of pairings over binary fields. They addressed
timing, SPA, and DPA attacks targeting arithmetic op-
erations. In order to propose a more efficient coun-
termeasure to protect Eta pairings, Kim et al. (Kim
et al., 2006) implemented the third countermeasure
proposed by Coron (Coron, 1999), which uses ran-
dom projective coordinates. The randomization coun-
termeasure proposed by Kim et al. adds just one step
at the beginning. For greater efficiency, when P is
secret, they randomized only the known input point
Q. Its effect is “removed” during the final exponenti-
ation.
This approach can be adapted to other pairing al-
gorithms that are based on either small or large char-
acteristic prime fields. This method is similar to the
countermeasure suggested by Scott (Scott, 2005). It
consists in randomizing the Miller variable in Algo-
rithm 1 by multiplying the operations 4 and 7 by a
random λ ∈ F
q
. The result is correct because the ran-
dom element is eliminated through the final exponen-
tiation.
In the end, these countermeasures only add few
modular multiplications, which means a small over-
head.
Whelan and Scott (Whelan and Scott, 2006) stud-
ied pairings with different base field characteristics.
They analyzed the arithmetic operations and con-
cluded that the secret can be recovered by using a
CPA. But the authors specified the need to have point
Q (second entry) as secret for the attack to work.
The latter conclusion was refuted in (El Mrabet et al.,
2009), which, to our best knowledge, is the first pa-
per to present a concrete attack on Miller’s algorithm
with P (first input) as secret.
Another attack, this time on an FPGA platform, is
proposed by Ghosh et al. (Ghosh and Roychowdhury,
2011). They performed a bitwise DPA attack on an
FPGA platform by measuring the power consumption
leakages during the modular subtraction operations.
To counteract this attack, the authors proposed a “low-
cost” protection based on a rearrangement principle
whose aim is to prevent interaction between a known
value and a secret input as it happens in the calcula-
tions involved in the tangent or line evaluations. To
achieve this, the authors proposed to rewrite the line
equation to prevent the addition and/or subtraction
operations between the known and secret data. They
used the distributivity properties, i.e. if an instruction
is (k −y
1
)y
2
with k being the secret and y
1
,y
2
being
known integers, then the target operation is (k −y
1
).
To avoid this, the authors proposed to rewrite it as
ky
2
−y
1
y
2
. Indeed, this trick avoids the critical sub-
traction. However, this time this trick does not protect
the modular multiplication and fails to protect against
classical attack schemes as presented in (El Mrabet
et al., 2009; Whelan and Scott, 2006) and (Bl
¨
omer
et al., 2013).
Moreover, Bl
¨
omer et al. (Bl
¨
omer et al., 2013)
studied DPA attacks by targeting modular addition
and multiplication operations of finite field elements
with large prime characteristics. Their paper de-
scribes an improved DPA for cases in which modular
addition is targeted by combining information derived
from manipulations of the least and most significant
bits. In addition, the study provided simulation results
to prove the feasibility of the attack. Furthermore,
they propose a new countermeasure. In the reduced
Tate pairing, the set of the second argument input is
the equivalence class
E(F
q
k
)
/lE(F
q
k
). If the random point
T is chosen initially from E(F
q
k
) of order r, coprime
to l, then T + Q ∼ Q. Hence, e(P,Q + T ) = e(P,Q).
This trick makes it possible to obtain a countermea-
sure as powerful as that of (Page and Vercauteren,
2004) with no overhead.
The importance of implementing countermea-
sures is supported by the recent results of Unterlug-
gauer and Wenger (Unterluggauer and Wenger, 2014)
and Jauvart et al. (Jauvart et al., 2016), where attacks
are presented in the real world environment. Indeed,
Ate pairings implemented on Virtex-II FPGA, ARM
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
107

Cortex-M0 and ARM Cortex-M3 have been broken
efficiently with CPA attacks.
Despite all this existing literature on side-channel
countermeasures for Pairings, to our best knowledge,
none have actually tested or validated the efficiency
of those countermeasures. In this paper we investi-
gate about the level of protection provided by the ran-
domization of coordinates which seems to be a classy
and efficient countermeasure. To our best knowledge,
no particular problem has been reported in the liter-
ature regarding this countermeasure applied to Pair-
ings. But our analysis shows that this countermeasure
can be defeated by a collision-based attack.
3.2 Collision based Side Channel
Attacks
The use of “collisions” as a means of exploiting side
channel attacks in not something new in the litera-
ture. In this section we provide a quick review of the
existing background in this very precise field before
describing our approach and the differences with the
existing state-of-the-art.
Collision attacks were first introduced
in (Schramm et al., 2003). The main idea is to
use the side-channel leakages to detect collisions in
the encryption function, such collisions may appear
internal to the function, in their attack it is not
mandatory to observe collisions only at the output.
Collisions inside the Data Encryption Standard (DES)
can be detected using side-channels and exploited
to retrieve the secret key used by the algorithm.
This new class of attack was later used to circumvent
countermeasures used in “secure” implementations of
the Advanced Encryption Standard (AES) in (Moradi
et al., 2010).
The use of collisions against implementations
of public key cryptographic algorithms have also
been described. To achieve this, Fouque and
Valette (Fouque and Valette, 2003) use the follow-
ing assumption: if two operations involve a common
operand then the use of this common operand, can
be detected using side-channels for attacking, in their
example, the RSA exponent. More precisely, even if
an adversary is not able to tell which computation is
done by the device, he can at least detect when the
device does the same operation twice. For example,
if the device computes 2.A and 2.B, the attacker is not
able to guess the value of A nor B but he is able to
check if A = B.
Similar work has been suggested by Bauer et al.
in (Bauer et al., 2013). This time the target is a scalar
multiplication over an elliptic curve. The assump-
tion is still the same: The adversary can detect when
two field multiplications have at least one operand
in common. In a double-and-add algorithm the dou-
bling step and the addition have a slight difference.
One of them (depending on the curve representation)
performs two modular multiplications with the same
operand. Collision detection allows to distinguish be-
tween the doubling and the addition operations, from
which the secret scalar can be deduced.
In (Varchola et al., 2015), the authors target a
protected Elliptic Curve Digital Signature Algorithm
(ECDSA) implementation. One of the weak points
of this protocol is the calculation of a modular mul-
tiplication between a known variable and the secret
key. Thus a DPA is able to recover the key (Hutter
et al., 2009). To counteract this attack, a trick con-
sists in distributing a calculus to remove such criti-
cal operations. As an example, whenever the opera-
tion mask(plaintext + public key ×secret key) must
be computed, they propose to do mask × plaintext +
(mask ×secret key)public key instead. The draw-
back revealed by Varchola et al. is that the additional
calculation is between the known message and the
temporary mask (which changes from one execution
to another) while another calculation is made between
this same mask and the secret. Thus, with the same
assumption that in the previous cases (Bauer et al.,
2013) and (Fouque and Valette, 2003), the collision
detection will make it possible to discover whether
the known (and controllable) message is equal to the
secret key.
Our contribution adapts the principle of collision
detection – based on the detecting when the same
operand is used twice – to circumvent the random-
ization of Jacobian coordinates countermeasure used
to protect pairing.
4 SECURITY ANALYSIS OF THE
COUNTERMEASURE BASED
ON RANDOMIZED JACOBIAN
COORDINATES
The previously described countermeasures have been
proposed without any theoretical security proofs, and
to the best of our knowledge, no practical evidence
has been provided neither. In this section, we an-
alyze one of these countermeasures: Miller’s algo-
rithm with randomized Jacobian coordinates. First,
we show how collisions can be used to make this
countermeasure fail. We introduce a first “straight-
forward” scheme to detect collisions and we show that
this approach has its limits in practice. Then we adapt
a refined method proposed in (Varchola et al., 2015)
SECRYPT 2017 - 14th International Conference on Security and Cryptography
108

for detecting collisions by implementing it on our tar-
get device and we show how practical results of how
this collision-detection scheme defeats the point ran-
domization countermeasure.
4.1 The Miller’s Algorithm with
Randomized Jacobian Coordinates
For performance reasons, the use of mixed affine-
Jacobian coordinates has been often proposed in the
literature (Aranha et al., 2011; Bajard and El Mra-
bet, 2007; Beuchat et al., 2010; Koblitz and Menezes,
2005) and (Naehrig et al., 2010). In this case, at the
beginning of the Miller’s algorithm, the point P is
assigned to T , with T expressed in Jacobian coordi-
nates. This operation comprises the following steps:
1. X
T
← x
P
; Y
T
← y
P
; Z
T
← 1,
2. T ← (X
T
: Y
T
: Z
T
).
The above steps are replaced by the proposed counter-
measure, for which the input point P is known, and Q
is the secret point:
1. λ ∈ F
?
q
is randomly generated,
2. X
T
← x
P
λ
2
; Y
T
← y
P
λ
3
; Z
T
← λ,
3. T ← (X
T
: Y
T
: Z
T
).
The full Miller algorithm that integrates this coun-
termeasure is given in Algorithm 2. In the end, the
mask λ is automatically removed in the final expo-
nentiation as λ
q
k
−1
l
= 1.
Algorithm 2: Miller’s algorithm with randomization
of Jacobian coordinates.
Data: l = (l
n−1
...l
0
) radix 2 representation,
P ∈ G
1
and Q ∈ G
2
Result: f
P
(D
Q
) ∈ G
3
1 λ ∈ F
?
q
is randomly generated ;
2 X
T
← x
P
λ
2
;
3 Y
T
← y
P
λ
3
;
4 Z
T
← λ;
5 f ←1;
6 for i = n −1 downto 0 do
7 f ← f
2
l
T,T
(Q)
v
[2]T
(Q)
;
8 T ← [2]T ;
9 if l
i
== 1 then
10 f ← f
l
T,P
(Q)
v
T +P
(Q)
;
11 T ← T + P;
12 end
13 end
14 return f ;
All attacks against pairings proposed so far are
DPA/CPA-like approaches that target arithmetic op-
erations such as modular additions or multiplications
between a known (public) value and a secret (key)
one. Our attack scheme is different in that it exploits
collisions which may appear during the same execu-
tion of a pairing.
Of course, since the recent results of Joux (Joux
et al., 2014) and Barbulescu (Barbulescu et al.,
2015a), pairings in small characteristic based field are
no longer recommended. Nevertheless, the proposed
countermeasures in such fields can also be used in
other fields with a very small overhead.
4.2 Detecting Collisions in
Point-randomized Pairing
Calculations
Our attack is based on the following observation: in
Algorithm 2 the mask is applied once to the pub-
lic parameter and at least once to the secret input.
During the first iteration of Miller’s loop, the tan-
gent evaluation calculates (xZ
2
T
−X
T
), which is in fact
(xλ
2
−x
P
λ
2
), for which xλ
2
is computed in the tan-
gent evaluation and x
P
λ
2
is computed in the random-
ization step.
Thus, if the known input x
P
is equal (or “par-
tially equal”) to the secret x, then the EM traces
are expected to be similar. The data x,x
p
are long
precision integers, for instance 256-bit integers, and
then it is impossible to test all the 2
256
values for
x. However, the targeted operations work on “word
reprensentations” of those integers, like for exam-
ple when implementing the Montgomey multiplica-
tion (Montgomery, 1985). So, we can consider only
one word of each of those integers. Even with this
remark, the words are still too long, for instance, a
256-bit integer can be stored in 8 words of 32 bits in
an 32-bit architecture. Then “partially equal” denotes
the equality of a part of the word such as the least
significant byte.
To exploit this observation, our proposed attack
scheme is the following. We assume that there exist
2
8
points P
j
such that the 8 LSBs (Least Significant
Bits) of the x coordinate cover all 2
8
possibilities.
x
P
0
= (? ? ···? 00000000)
2
x
P
1
= (? ? ···? 00000001)
2
.
.
.
x
P
255
= (? ? ···? 11111111)
2
We then perform a pairing between each P
j
and
the secret point Q. The λ
j
value is chosen at random.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
109

For each EM trace, it is necessary to focus on two
critical moments: the computations of x
P
j
λ
2
j
and xλ
2
j
.
For each of the resulting “pairs of traces”, we need
to evaluate the similarities between the two signals.
These similarities can be estimated through cross cor-
relations for example. The maximum correlation co-
efficient then yields a candidate for the 8 LSBs of the
secret x.
Averaging is necessary to reduce the effect of
noise on the attack. Obviously, due to the randomness
of λ, it is not recommended to average the acquired
traces. However, for a fixed input x
P
j
and x, we com-
puted the cross correlations between traces for x
P
j
λ
2
and xλ
2
computations. We thereby obtain c
(0)
P
j
, and
we repeat the process with other unknown λ. We then
collect some c
(n)
P
j
coefficients for each key hypothesis
and subsequently compute an average correlation co-
efficient for all hypothetical keys. This number n is
further denoted n
times P.
We subsequently repeat the method with other val-
ues of P
j
covering another portion of the data, and the
secret is fully recovered.
5 PRACTICAL
IMPLEMENTATION OF THE
COLLISION ATTACK AGAINST
POINT RANDOMIZATION
In this section, we report the practical results obtained
when implementing our collision attack. The exper-
iments were carried in two stages. A first stage con-
sisted in testing the feasibility of detecting collisions,
at word level, on our 32-bit target device. In the sec-
ond stage, we implemented our attack on a Pairings
implementation integrating Jacobian point randomi-
sation countermeasure.
5.1 Preliminary Characterization of
Collision Detection on our Target
Device
The targeted device is an ARM Cortex M3 processor
working on 32-bit registers. We implemented the rep-
resentative target operations over 32-bit integers:
• x
P
j
×λ
2
,
• x ×λ
2
.
As source of side channel information, we use
the ElectroMagnetic (EM) waves emitted by the chip
during the targeted calculations. This technique does
not need any depackaging of the chip and allowed to
have “local” measurements when precisely positioned
on top of the die. The electromagnetic emanation
(EM) measurements were done using a Langer EMV-
Technik LF-U 5 probe equipped with a Langer Am-
plifier PA303 BNC (30dB). The curves were collected
using a Lecroy WaveRunner 640Zi oscilloscope. The
acquisition frequency of the oscilloscope is 10
9
sam-
ples per second. The EM measurements acquisition is
done as in Algorithm 3.
Algorithm 3: EM measurements acquisition proce-
dure.
Data: n times P, the repetition number
Result: A data base of EM measurement
R ∈ M
256,n times P,2t
, t is the traces
length
1 for j = 0 to 255 do
2 x
j
← (0...0 j
7
j
6
... j
0
)
2
; // j = ( j
7
... j
0
)
2
in radix 2 representation
3 for i = 0 to n times P −1 do
4 λ ← random in {0,. . . , 2
32
−1};
5 Execute the routine: computation of
x
j
×λ
2
, x ×λ
2
;
6 Store the EM measurement in R[ j,i]
7 end
8 end
9 return R;
As a result, in one EM measurement there are two
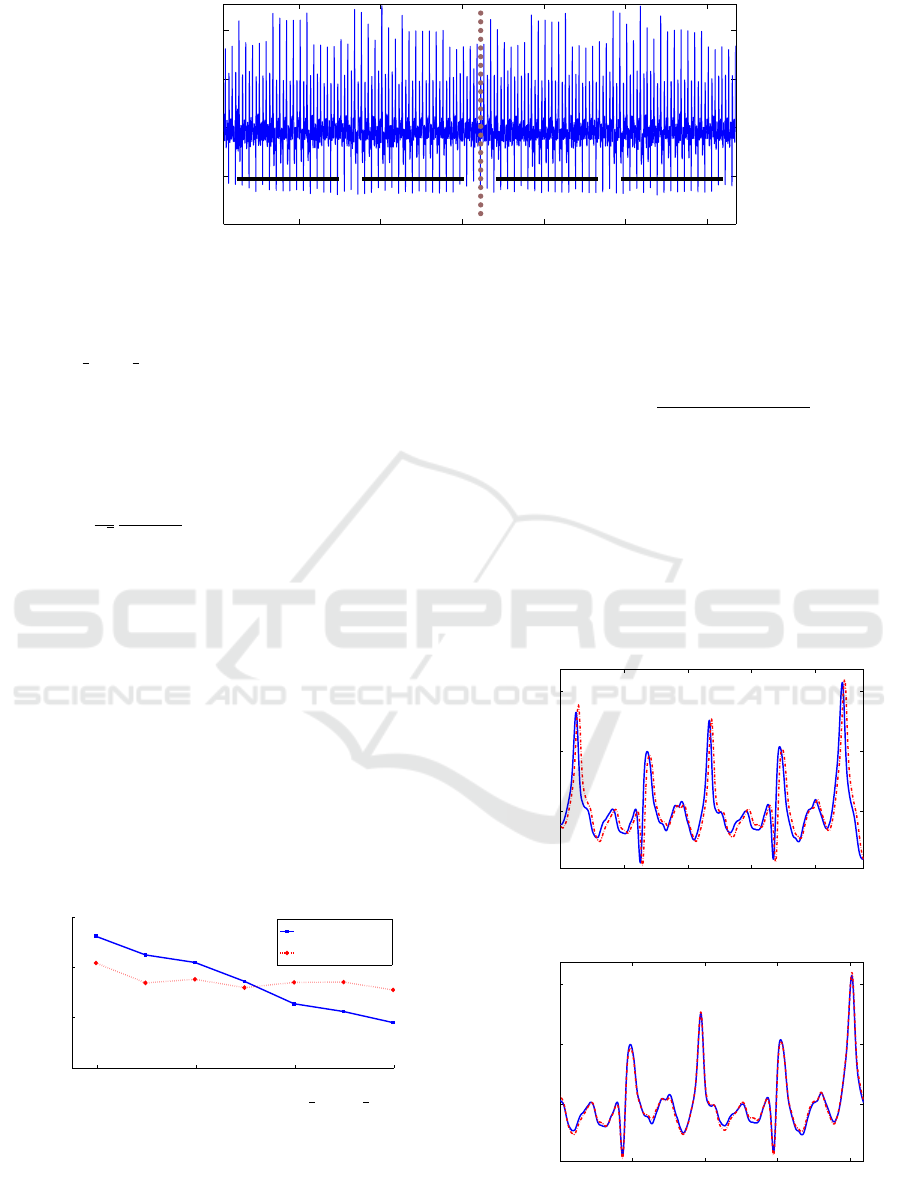
multiplications. An example of such a trace is given
in Figure 1.
The choice of EM leakages source is justified by
the fact that the device under test is not appropriate
for acquiring power consumption. Indeed, the device
has many power sources and grounds, so if we want
to keep the power consumption, the choices of them
is not so simple, and can be a combination of sev-
eral sources/grounds. The other reason is linked to the
practical equipment to make the power consumption
attack. A resistance should be placed on the source or
on the ground, then there is a risk of damaging the cir-
cuit. The EM equipment is just a probe to place over
the integrated circuit. Furthermore, in the case of our
device, it is not necessary to depackage to integrated
circuit, then there is no dangerous manipulation of the
circuit.
At the end of Section 4.2 we introduced the the-
oretical technique to distinguish the good key when
the correlation coefficient is used to detect collisions.
This naive method consists in comparing two traces
by cross correlation for each couple x
P
j
× λ
2
and
x ×λ
2
, and computes a coefficient for each key hy-
SECRYPT 2017 - 14th International Conference on Security and Cryptography
110

0.5 1 1.5 2 2.5 3
x 10
4
−0.1
0
0.1
0.2
Number of samples (time)
Amplitude (V)
| {z }
x
P
j
λ
2
|
{z }
xλ
2
1
Figure 1: An example of electromagnetic emanation measurement.
pothesis (denoted by x
P
j
) by averaging the correlation
over the n times P repetitions.
We used this method with our EM measurements
by using the correlation criterion and another one,
named BCDC (Bounded Collisions Detection Crite-
rion). As shown in (Diop et al., 2015), this criterion
detection can be used instead of correlation. This cri-
terion takes two traces C
1
and C
2
, compares them by
computing
1
√
2
σ(C
1
−C
2
)
σ(C
1
)
and returns a value in [0,1]. A
collision is detected if the value of BCDC is close to
0. The notation σ(C
1
) denotes the standard deviation
of the leakage vector C
1
while σ(C
1
−C
2
) is the stan-
dard deviation of the difference C
1
−C
2
.
The attack succeeds if the maximal value for the
collision detection criterion is reached when x
P
j
= x.
Then we can classify the key candidates (on 8 bits)
according to their criterion values. The keys are now
ranked from the most to the least probable, the posi-
tion of the correct secret key is called the “key rank-
ing”. The key ranking is a value between 1 and 256,
it is worth 1 if the attack succeeds in recovering the
secret’s least significant byte.
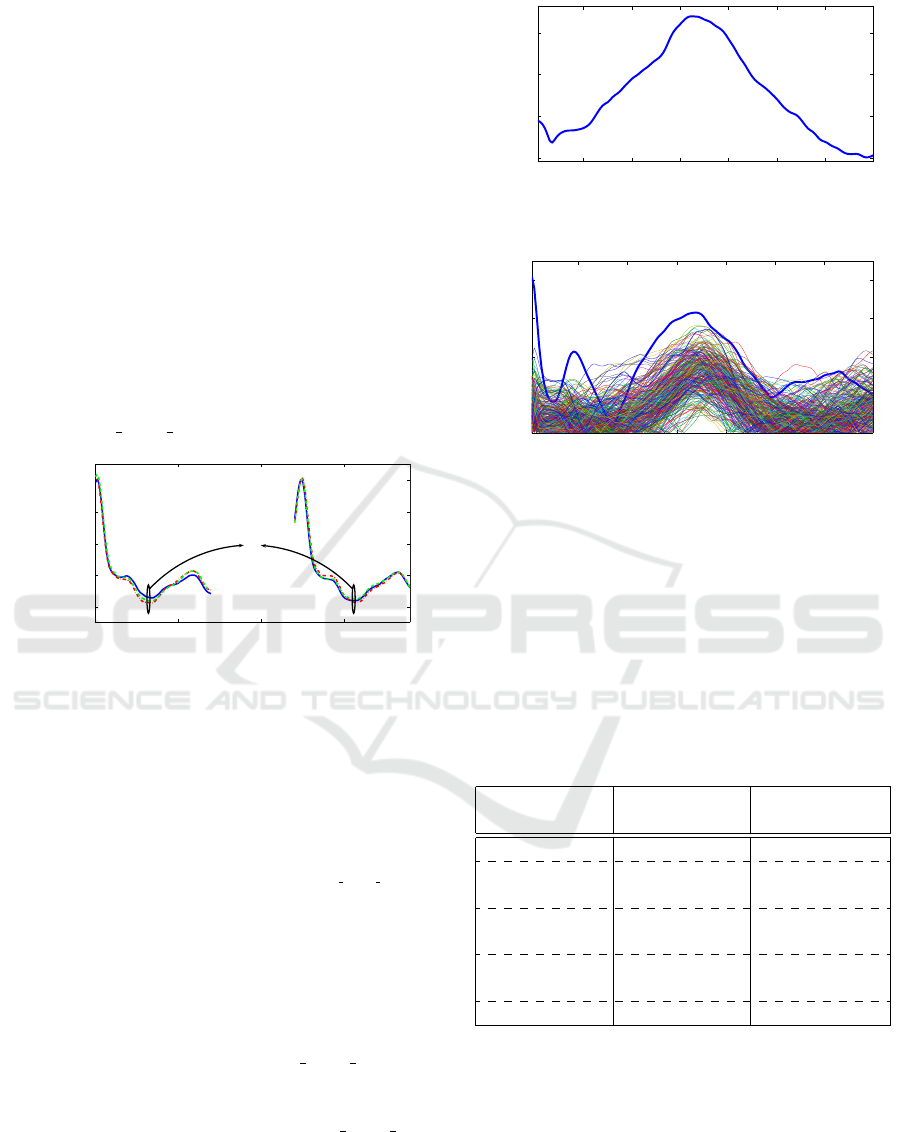
Figure 2 shows that the key ranking slightly de-
creases with the number of traces used for the attack.
100 200 300 400
40
60
80
100
Number of traces per key (n times P )
Key ranking
Key ranking for correlation and BCDC
Correlation
BCDC
Figure 2: Results for a naive collision attack.
The method does not provide convincing results
even if we use more EM measurements.
In this approach the comparison is horizontal. In-
deed, the EM measurements C
1
and C
2
are sampled
over t points, the returned coefficient is the cross cor-
relation computed with the Pearson coefficient:
ρ(C
1
,C
2
) =
covariance(C
1
,C
2
)
σ(C
1
)σ(C
2
)
. (5)
The main drawback of this method is the need to
perfectly align the traces as the correlation coefficient
largely depends on the adjustment of the traces’ po-
sition. The toy example in Figures 3 and 4 of EM
measurement show the great dependency between the
coefficient correlation and the alignment of traces.
This small demonstration and our practical experi-
ences convinced us to use another collisions detection
techniques.
0 200 400 600 800
0
0.1
0.2
2 traces sans alignement
Number of samples (time)
Amplitude (V)
ρ =0.8297
Figure 3: Traces without retouching.
0 200 400 600 800
0
0.1
0.2
2 traces avec alignement
Number of samples (time)
Amplitude (V)
ρ =0.9962
Figure 4: Shifted traces on 7 points sample.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
111

Due those bad results we investigate another tech-
nique for detecting collisions.
5.1.1 Advanced Collisions Detection
The aim this time is to detect if there exists a link in
the EM measurements during the two targeted mul-
tiplications using “vertical correlations” as initially
proposed (Varchola et al., 2015).
Instead of comparing the traces between each
other and giving a coefficient that indicates whether
there is a collision, it is a point-to-point comparison
(where each point is a temporal instant within each
trace).
Figure 5 illustrates this principle. The left pat-
tern corresponds to the multiplication x
P
j
×λ
2
and the
other one corresponds to the operation x ×λ
2
. For
the sake of have “clear” pictures, Figure 5 only shows
three traces (n times P = 3).
0 100 200 300
−0.05
0
0.05
0.1
0.15
Number of samples (time)
Amplitude (V)
3 traces en TM1 et TM2
ρ
1
Figure 5: Vertical correlation collision principle.
The trick proposed by Varchola et al. (Varchola
et al., 2015) to avoid the synchronization problem is
to select a time instant in the first multiplication, a
window in the second one and drag the single vector
on the window to compute t correlations.
More precisely, for a fixed known input x
P
j
, the
collected EM measurements are R
j
∈ M
n times P,2t
as
we have seen in Algorithm 3. The result R is like the
matrix in Equation 6.
From there, the attacker builds a “correlation
trace” corr
j
∈ M
1,t
for a chosen time instant t
interset
with corr
j
defined in Equation 7.
To illustrate the general shape of such a “correla-
tion trace” we refer the reader to Figure 6. For this ex-
ample we make a toy example with n times P = 100.
As in classical side-channel attacks, the highest
correlation allows to identify the most probable key
(the thickest blue curve in Figure 7, with n times P =
400).
20 40 60 80 100 120 140
−0.1
0
0.1
0.2
correlation verticale
Number of samples (time)
Correlation
Figure 6: Vertical correlation collision toy example.
20 40 60 80 100 120 140
0
0.1
0.2
0.3
0.4
Number of samples (time)
|Correlation|
Figure 7: Vertical correlation collision.
5.1.2 Practical Results using the Advanced
Collision Detection
In (Varchola et al., 2015), the collision attack’s suc-
cess is supported by practical results. Their target is
an 8-bit hardware implementation on an FPGA, their
board was designed especially for the purpose of side-
channel analyses. So, our experimental works are dif-
ferent in several points (see Table 1).
Table 1: Difference between target and set-up.
Settings
(Varchola
et al., 2015)
Our case
Device FPGA Microcontroller
Architecture
size
8-bit 32-bit
Clock
frequency
16.384 MHz 50 MHz
Sampling
frequency
20 Gsps 10 Gsps
side-channel Power EM
The main difference is of course the target of eval-
uation, hardware in their case and software in ours.
Another important difference comes from the archi-
tecture as the attack targets the 8 least significant bits
but the manipulated data are on 32 bits with the de-
vice producing leakages related to the 32-bit manipu-
lated data. Therefore, unlike (Varchola et al., 2015),
our 256 keys hypothesis do not cover all the possible
sought secret value.
SECRYPT 2017 - 14th International Conference on Security and Cryptography
112

R
j
=






C
(1)
1,1
C
(1)
1,2
... C
(1)
1,t
C
(1)
2,1
... C
(1)
2,t
C
(2)
1,1
... C
(2)
1,t
C
(2)
2,1
... C
(2)
2,t
.
.
.
.
.
.
.
.
.
.
.
.
C
(n times P)
1,1
... C
(n times P)
1,t
C
(n times P)
2,1
... C
(n times P)
2,t






. (6)
corr
j
(i) = ρ








C
(1)
1,t
interest
.
.
.
C
(n times P)
1,t
interest




,




C
(1)
2,i
.
.
.
C
(n times P)
2,i








,∀i = 1,...,t (7)
Hence the question is the following: the traces
are from 32-bit manipulated data, will the leakages
be sufficiently meaningful to target only 8 bits at a
time? Our attack is a chosen ciphertext attack be-
cause the x
P
j
have a particular shape, indeed, x
P
j
=
(00...0 j
7
j
6
... j
0
)
2
In our experimentation we chose n times P = 400
and hence we have the attack results presented in Fig-
ure 8 (green squares). Each score is obtained by aver-
aging the results for 100 attacks with different traces.
These figures show the ranking of the correct key (8
least significant bits) among the 256 possible ones.
The guess is correct when the rank equals to one. This
ranking decreases with the number of traces in a sig-
nificant way.
50 100 150 200 250 300 350 400
0
10
20
30
40
50
Number of traces per key (n times P )
Key ranking
Byte 2
Byte 1
Figure 8: Key ranking for the attack against the least signif-
icant byte and the following byte.
The attack recovers, the 8-bit key when the num-
ber of trace per key n times P is close to 400 (i.e. a
total of EM measurement close to n times P ×2
8
=
400 ×256 = 102400). The secret key can be easily
discriminated in a small set of candidates, resulting a
huge loss of entropy.
5.2 Recovering the Full 256 Secret Bits
Integer with Collisions
In order to recover the full secret point during the Tate
pairing calculation that we implemented and that we
run on our 32-bit platform, we applied the method de-
scribed previously to the other bytes, within the same
32-bit word first, and then for the other 32-bit words,
in order to recover the full 256-bit secret integer. The
used BN curves to implement the Tate pairing are set
for t = 3FC0100000000000 (in hexadecimal).
The attack on the other bytes is very similar to
what has been described so far in the “advanced” tech-
nique. The known inputs x
P
j
are different: they first
“integrate” the 8 least significant bits recovered by
the first step of the attack as carried in the previous
section. Let (
b
x
7
b
x
6
...
b
x
0
)
2
=
b
x be the 8 least signifi-
cant bits recovered by the attack, then the chosen ci-
phertext is x
P
j
= (00 ...0 j
7
j
6
... j
0
b
x
7
b
x
6
...
b
x
0
)
2
. Now,
when j will have the same value as the secret, there
will be a collision not only on 8 bits but also on 16
bits. When the 16 bits manipulated in the multipli-
cations will be the same, the collision will be easier
to detect than when there were only 8 identical bits.
Practical results are provided in Figure 8 (red stars).
It shows that the attack is easier as soon as the least
significant bits are known. With only n times P =
300, the attack succeeds.
In the 32-bit word two bytes are still unknown.
The same attack method allows us to recover these 32
secret bits. To attack the other words of the integer is
not more complicated, everything relies on the proper
understanding of the multiplication algorithm.
5.2.1 The Cost of Carrying the Attack
Our targeted Pairings implementations involve 256-
bit length integer arithmetic. That is, since there are 8
words of 32-bit integer, then the previous attack needs
to be performed 8 times. But, the messages (x
P
) are
chosen, so we can construct such x
P
to recover the 8
words at the same time. It is like a parallel process :
1. Setting the messages x
P
j
=

X
j,7
,X
j,6
,...,X
j,0

with the X
j,i
32-bit word which are the x
P
j
of sec-
tion 5.1.2 and capture the side-channel leakages.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
113

2. For each i = 0,...,7 make the attack to recover
the 8 LSBs of each X
i
.
3. Start again with the second least significant bits of
X
i
.
Thus, the attack to find the 256 bits does not re-
quire 8 times more traces than the one we presented
to recover 32 bits. There are 8 independent attacks,
but not 8 times more traces.
Thus, the number of traces required to break the
x
Q
coordinates of the secret input is:
E ' 2
8
(400 + 3 ×300) ' 3.5 ×10
5
To compare with the attack against the non-
protected version, recent results (Jauvart et al., 2016)
show an attack with an averages of 200 traces to re-
cover one word, so 8 ×200 = 1600 for the entire
256-bits secret integer. Then the countermeasure con-
strains the attacker to achieve 200 times more power
measurements. In our experiment, one trace is ac-
quired in an average of 0.4 second. Thus, the collision
attack on the protected implementation take 2 days to
recover the secret x
Q
.
6 CONCLUSION
Several recent publications have addressed side-
channel attacks against pairing-based cryptography.
The present paper provides an overview of the dif-
ferent SCA schemes and a description of the coun-
termeasures proposed to circumvent such attacks. To
the best of our knowledge, these countermeasures
have been proposed without any (theoretical or prac-
tical) security proofs. Our investigation thus consti-
tutes the first critical analysis of the efficiency of one
of these countermeasures. We have shown that the
countermeasure based on point randomisation can be
defeated using a collision-based side-channel attack.
We also propose a method for improving the number
of required curves for our attack. We have validated
the feasibility of our attack against a pairing calcula-
tion which has been protected using this countermea-
sure.
At this stage we can therefore recommend to also
randomize the secret at the beginning of the pair-
ing. The randomization of Jacobian coordinates of
the secret implies the non-reportion of the operation
between the mask and the secret, and thus our com-
ment on the collision is no longer valid. Moreover, to
set the secret in Jacobian coordinates implies that the
equations of the tangent and of the line are no longer
in mixed coordinates (Equation 4). Then the gener-
ated overhead is eight modular multiplications (three
in the computation of the tangent and five in the line).
Our analysis highlights the difficulty in devis-
ing countermeasures that protect implementations of
complex cryptographic functions such as pairings
against physical attacks. For such algorithms, tools
should be developed to test whether the randomness
properties that are initially introduced into a pairing
calculation are sufficiently propagated across the en-
tire computation, at least for as long as the secret point
is still involved in the calculation.
Finally, recent papers (Kim and Barbulescu, 2015;
Barbulescu et al., 2015b; Menezes et al., 2016) show
new improvements in the algorithms used to solve dis-
crete logarithm, in particular over BN curves. Those
latter developments only require the redefinition of
the Pairings’ parameters and key sizes, in which case,
in our opinion, our attack scenario would still hold as
our attack is independent of the choice of the curve.
ACKNOWLEDGEMENTS
This work was supported in part by the EUREKA
Catrene programme under contract CAT208 Mobi-
Trust and by a French DGA-MRIS scholarship.
REFERENCES
Aranha, D. F., Karabina, K., Longa, P., Gebotys, C. H.,
and L
´
opez, J. (2011). Faster Explicit Formulas for
Computing Pairings over Ordinary Curves. In EURO-
CRYPT, pages 48–68. Springer.
Bajard, J. and El Mrabet, N. (2007). Pairing in cryptog-
raphy: an arithmetic point of view. Advanced Signal
Processing Algorithms, Architectures, and Implemen-
tations.
Barbulescu, R., Gaudry, P., Guillevic, A., and Morain, F.
(2015a). Improving NFS for the discrete logarithm
problem in non-prime finite fields. In EUROCRYPT,
pages 129–155. Springer.
Barbulescu, R., Gaudry, P., and Kleinjung, T. (2015b). The
Tower Number Field Sieve. In Iwata, T. and Cheon,
J. H., editors, ASIACRYPT 2015, volume 9453, pages
31–58. Springer.
Barreto, P., Kim, H., Lynn, B., and Scott, M. (2002). Effi-
cient algorithms for pairing-based cryptosystems. In
CRYPTO 2002, pages 354–396. Springer.
Barreto, P. S. L. M. and Naehrig, M. (2005). Pairing-
Friendly Elliptic Curves of Prime Order. SAC’05,
pages 319–331, Berlin, Heidelberg. Springer-Verlag.
Bauer, A., Jaulmes, E., Prouff, E., and Wild, J. (2013). Hori-
zontal Collision Correlation Attack on Elliptic Curves.
SAC’13, pages 553–570. Springer.
Beuchat, J.-L., Gonz
´
alez-D
´
ıaz, J. E., Mitsunari, S.,
Okamoto, E., Rodr
´
ıguez-Henr
´
ıquez, F., and Teruya,
T. (2010). High-speed software implementation of the
SECRYPT 2017 - 14th International Conference on Security and Cryptography
114

optimal ate pairing over barreto–naehrig curves. In
ICPBC, pages 21–39. Springer.
Bl
¨
omer, J., G
¨
unther, P., and Liske, G. (2013). Improved
Side Channel Attacks on Pairing Based Cryptography.
COSADE, 7864:154–168.
Boneh, D. and Franklin, M. (2001). Identity-Based En-
cryption from the Weil Pairing. In Advances in Cryp-
tology - CRYPTO 2001, volume 32, pages 213–229.
Springer.
Coron, J. (1999). Resistance against Differential Power
Analysis for Elliptic Curve Cryptosystems. CHES,
pages 292 – 302.
Diop, I., Liardet, P.-Y., Linge, Y., and Maurine, P. (2015).
Collision based attacks in practice. In DSD, pages
367–374. IEEE.
Duursma, I. and Lee, H. (2003). Tate Pairing Implemen-
tation for Hyperelliptic Curves y
2
= x
p
−x + d. ASI-
ACRYPT, 4:111–123.
Eisentr
¨
ager, K., Lauter, K., and Montgomery, P. L. (2004).
Improved weil and tate pairings for elliptic and hyper-
elliptic curves. In International Algorithmic Number
Theory Symposium, pages 169–183. Springer.
El Mrabet, N., Di Natale, G., Flottes, and Lise, M. (2009). A
Practical Differential Power Analysis Attack Against
the Miller Algorithm. PRIME, pages 308–311.
Fouque, P.-A. and Valette, F. (2003). The Doubling Attack –
Why Upwards Is Better Than Downwards. In CHES,
pages 269–280. Springer.
Galbraith, S., Harrison, K., and Soldera, D. (2002). Im-
plementing the Tate Pairing. In Algorithmic Number
Theory, pages 324–337. Springer.
Ghosh, S. and Roychowdhury, D. (2011). Security of
prime field pairing cryptoprocessor against differen-
tial power attack. In Security Aspects in Informa-
tion Technology, volume 7011 LNCS, pages 16–29.
Springer.
Hutter, M., Medwed, M., Hein, D., and Wolkerstorfer, J.
(2009). Attacking ECDSA-Enabled RFID devices.
Applied Cryptography and Network Security, pages
519–534.
Jauvart, D., Fournier, J. J.-A., El Mrabet, N., and Goubin,
L. (2016). Improving Side-Channel Attacks against
Pairing-Based Cryptography. In Risks and Security of
Internet and Systems. Springer.
Joux, A. (2004). A one round protocol for tripartite Diffie-
Hellman. Journal of Cryptology.
Joux, A., Odlyzko, A., and Pierrot, C. (2014). The Past,
evolving Present and Future of Discrete Logarithm.
In Open Problems in Mathematics and Computational
Science, pages 1–23. Springer.
Kim, T. and Barbulescu, R. (2015). Extended Tower Num-
ber Field Sieve: A New Complexity for the Medium
Prime Case. Cryptology ePrint Archive.
Kim, T. H., Takagi, T., Han, D.-G., Kim, H. W., and Lim, J.
(2006). Side Channel Attacks and Countermeasures
on Pairing Based Cryptosystems over Binary Fields.
Cryptology and Network Security, pages 168–181.
Koblitz, N. and Menezes, A. (2005). Pairing-based cryp-
tography at high security levels. Cryptography and
Coding, 3796 LNCS:13–36.
Kocher, P., Jaffe, J., and Jun, B. (1999). Differential power
analysis. Advances in Cryptology - CRYPTO’99,
pages 1–10.
Menezes, A., Sarkar, P., and Singh, S. (2016). Challenges
with Assessing the Impact of NFS Advances on the
Security of Pairing-based Cryptography. Cryptology
ePrint Archive.
Miller, V. (1986). Use of elliptic curves in cryptography.
CRYPTO ‘85, 218:417–426.
Montgomery, P. L. (1985). Modular multiplication without
trial division. In Mathematics of Computation, vol-
ume 44, pages 519–519.
Moradi, A., Mischke, O., and Eisenbarth, T. (2010).
Correlation-Enhanced Power Analysis Collision At-
tack. In CHES, pages 125–139. Springer.
Naehrig, M., Niederhagen, R., and Schwabe, P. (2010).
New software speed records for cryptographic pair-
ings. In LATINCRYPT, pages 109–123. Springer.
Page, D. and Vercauteren, F. (2004). Fault and Side-
Channel Attacks on Pairing Based Cryptography.
IEEE Transactions on Computers.
Pan, W. and Marnane, W. (2011). A correlation power anal-
ysis attack against Tate pairing on FPGA. Reconfig-
urable Computing: Architectures, Tools and Applica-
tions.
Schramm, K., Wollinger, T., and Paar, C. (2003). A
New Class of Collision Attacks and Its Application
to DES. In Fast Software Encryption, pages 206–222.
Springer.
Scott, M. (2005). Computing the Tate pairing. CT-RSA,
pages 293–304.
Silverman, J. H. (2009). The Arithmetic of Elliptic
Curves, volume 106 of Graduate Texts in Mathemat-
ics. Springer-Verlag, 2nd edition.
Unterluggauer, T. and Wenger, E. (2014). Practical Attack
on Bilinear Pairings to Disclose the Secrets of Embed-
ded Devices. ARES, pages 69–77.
Varchola, M., Drutarovsky, M., Repka, M., and Zajac, P.
(2015). Side channel attack on multiprecision mul-
tiplier used in protected ECDSA implementation. In
ReConFig, pages 1–6.
Whelan, C. and Scott, M. (2006). Side Channel Analysis
of Practical Pairing Implementations: Which Path Is
More Secure? VIETCRYPT 2006, pages 99–114.
First Practical Side-channel Attack to Defeat Point Randomization in Secure Implementations of Pairing-based Cryptography
115