Compression Techniques for Deep Fisher Vectors
Sarah Ahmed and Tayyaba Azim
Center of Excellence in IT, Institute of Management Sciences, Peshawar, Pakistan
Keywords:
Fisher Vectors (FV), Restricted Boltzmann Machine (RBM), k-Nearest Neighbor (k-nn), Principal Component
Analysis (PCA), Parametric t-SNE, Spectral Hashing.
Abstract:
This paper investigates the use of efficient compression techniques for Fisher vectors derived from deep ar-
chitectures such as restricted Boltzmann machine (RBM). Fisher representations have recently created a surge
of interest by proving their worth for large scale object recognition and retrieval problems due to the intrinsic
properties that make them unique from the conventional bag of visual words (BoW) features, however they
suffer from the problem of large dimensionality. This paper provides empirical evidence along with visualisa-
tions to explore which of the feature normalisation and state of the art compression techniques is well suited
for deep Fisher vectors, making them amenable for large scale visual retrieval with reduced memory footprint.
We further show that the compressed Fisher vectors give impressive classification results even with costless
linear classifiers like k-nearest neighbour.
1 INTRODUCTION
Large scale image classification and retrieval has re-
ceived an increasing attention over the last decade
due to the large amount of multimedia data availabil-
ity on the web and the growing need to mine infor-
mation of interest from these large image reposito-
ries. Where on one end, we have witnessed improve-
ments in the hardware to efficiently store and pro-
cess such massively growing data sets, efforts have
also been made at the algorithmic level to come up
with speedy retrieval techniques that are human com-
petitive in perception and image understanding tasks.
These algorithms rely specifically on how the images
are represented semantically in a feature space that
makes them discriminant as well as retrievable for
later use. In this regard, one of the most popular ap-
proaches to represent images through mid level fea-
tures is bag of visual words (BoW) approach (Csurka
et al., 2004) that converts the visual vocabulary built
in low level feature space into intermediate represen-
tations of fixed size to train a non-linear classifier
like support vector machines (SVM) and have consis-
tently shown to outperform other methods in succes-
sive PASCAL VOC evaluations (Everingham et al.,
2015). However, an important limitation of this ap-
proach lies in its inability to scale to large amounts
of training data. The computational cost of non-
linear SVMs is between O(N
2
) and O(N
3
), thus mak-
ing it unattractive for large scale image classification
and retrieval problems. Attempts have been made
to reduce the computational cost incurred in training
non-linear SVMs by either changing the classifier or
choosing a better encoding scheme (Farquhar et al.,
2005), (Perronnin et al., 2006), (Boureau et al., 2010),
(Wang et al., 2010), (Lazebnik et al., 2006) that can
perform well even with a linear classifier.
The Fisher kernel (FK) framework introduced by
Jaakola et al. (Jaakkola and Haussler, 1998) and ap-
plied by Perronin et al. (Perronnin and Dance, 2007)
for image classification task is an extension of bag of
visual words (BoW) approach and is explained in de-
tail in Section 2. The FK representation overcomes
the limitations of BoW approach (Perronnin et al.,
2010) and has yielded competitive results for large
scale image classification and retrieval tasks (Chat-
field et al., 2011), (Perronnin and Larlus, 2015). It
combines the benefits of generative and discrimina-
tive approaches to pattern classification by deriving
a kernel from a generative probability model of the
data. Another prominent feature of the Fisher vectors
is that they perform very well even with a simple lin-
ear classifier using techniques such as stochastic gra-
dient descent method. However, these recommended
Fisher features have high dimensionality and in com-
bination with a large number of examples could pose
computational and storage constraint (Sanchez et al.,
2013). This problem has been tackled by either us-
ing standard compression techniques (Sanchez et al.,
2013) or through feature selection methods (Zhang
Ahmed, S. and Azim, T.
Compression Techniques for Deep Fisher Vectors.
DOI: 10.5220/0006205002170224
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 217-224
ISBN: 978-989-758-222-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
217

et al., 2014) that reduce the signature length of each
image to acquire less storage and quick retrieval re-
sults.
This paper takes into account a different class of
Fisher vectors derived from a deep stochastic model,
i.e. restricted Boltzmann machine (RBM) (Azim and
Niranjan, 2013) and analyses efficient ways of com-
pressing its dimensionality to achieve minimal loss in
classification performance. The dimensionality of the
Fisher vectors derived from deep models has an in-
trinsic relationship with the number of hidden units
of the model. The length of the encoded Fisher vec-
tor increases as the number of hidden units increase.
See Table 1 for illustration of the impact of model’s
architecture on Fisher vector’s length. Our goal is to
reduce the Fisher feature dimensionality and hence
the storage cost and computational load of the re-
trieval algorithm. Our contributions are as follows: a)
Analysing a different class of Fisher vectors for large
scale image classification, b) Sparsity analysis of the
Fisher vectors derived from RBM, c) Demonstrating
visualisations of compressed Fisher vectors through
off the shelf available compression techniques, d)
Highlighting the type of feature normalisation scheme
required to achieve better Fisher scores density and
classification performance.
Table 1: Growth of Fisher vector’s length on MNIST data
set where the images have dimensionality 28 × 28. The
length, l = |v| × |h| when gradients with respect to the
weights, W between visible and hidden units are considered
only.
RBM Hidden Units 1 10 100 1000 10000
FV’s Length 784 7840 78400 784000 7840000
l = |∇
W
logP(x
n
|θ)|
2 THE FISHER KERNEL
FRAMEWORK
The Fisher kernel framework introduced by Jaakola
and Haussler (Jaakkola and Haussler, 1998) proposes
to use a generative probability model, P(x|θ) to de-
rive a kernel by computing Fisher scores using gradi-
ents of the log likelihood of the data, x with respect to
the model parameters, θ. The derived kernel function
thus takes the form:
K(x
i
,x
j
) = φ
T
x
i
U
−1
φ
x
j
, (1)
where U is the covariance matrix of the Fisher scores,
φ
x
and is regarded as Fisher Information matrix. The
computation of Fisher information matrix is generally
considered immaterial (Jaakkola and Haussler, 1998)
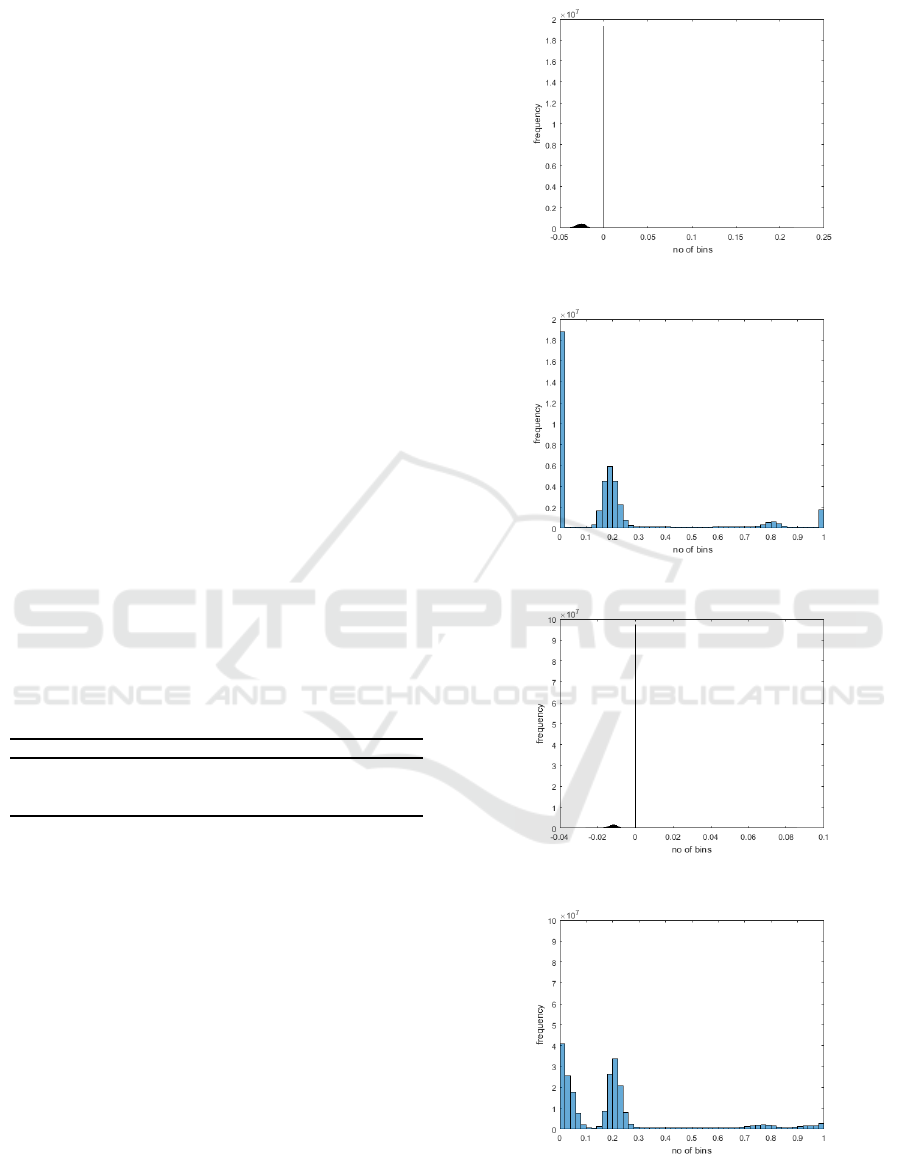
(a) Before normalisation, MNIST Fisher vec-
tors derived from RBM with 1 hidden unit.
(b) After normalization, MNIST Fisher vectors
derived from RBM with 1 hidden unit.
(c) Before normalisation, MNIST Fisher vec-
tors derived from RBM with 5 hidden units.
(d) After normalization, MNIST Fisher vectors
derived from RBM with 5 hidden units.
Figure 1: Histogram of the Fisher scores calculated before
and after the application of min-max feature normalisation.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
218

and is often ignored in practice by replacing it with
an identity matrix, I. However, some of the literature
on the classification systems has shown good discrim-
ination results by using approximations of the infor-
mation matrix in kernel computation (Maaten, 2011).
Examples of such approximations include restricted
forms of covariancematrix, such as a diagonal covari-
ance matrix (U = diagonal(σ
2
)) or isotropic Gaus-
sians (U = σ
2
I). Fisher kernel, once derived from a
generative probability model, P(x|θ) is capable of be-
ing embedded into any discriminative classifier such
as support vector machines (SVM), linear discrimi-
nant analysis (LDA), neural networks, etc.
In this work, we have taken a restricted Boltz-
mann machine (RBM) (Hinton, 2002) to deriveFisher
scores. A restricted Boltzmann machine is a bipar-
tite graph in which the visible units that represent
observations are connected to binary stochastic hid-
den units using undirected weight connections. The
hidden units are used to discover useful features or
patterns from the data fed to the visible layer during
training. The probability of a joint configuration over
both visible and hidden units depends on the energy
of that joint configuration compared with the energy
of all other joint configurations:
P(v,h;θ) =
1
Z(θ)
exp(E(v,h, θ)), (2)
where the partition function, Z(θ) is given as:
Z(θ) =
∑
v,h
exp(E(v,h,θ)).
The parameters of this energy based model are learnt
by performing stochastic gradient descent learning on
the empirical negative log- likelihood of the training
data. A guide to initialise and optimise these parame-
ters, θ = {W, a, b} is given by Hinton (Hinton, 2010).
The Fisher scores, φ
x
derived from the gradients of
the log likelihood of the data, x with respect to RBM
model parameters, θ = {W,a,b} are given as below:
∇
θ
logP(x
n
|θ) =

S
[n]
| Q
[n]
| Z
[n]

,where (3)
S
[n]
= ∇
W
logP(x
n
|θ) = hvh
T
i
P
data
− hvh
T
i
P
model
,
(4)
Q
[n]
= ∇
a
logP(x
n
|θ) = hhi
P
data
− hhi
P
model
, (5)
Z
[n]
= ∇
b
logP(x
n
|θ) = hvi
P
data
− hvi
P
model
. (6)
3 THE FISHER VECTOR
NORMALISATION
In this section, we describe the normalisation scheme
required for achieving competitive classification re-
sults on deep Fisher vectors with a linear classifier.
We have applied Min-Max normalisation technique
(Jayalakshmi and Santhakumaran, 2011) on the de-
rived Fisher vectors. This method re-scales our fea-
tures in the range [0, 1]. If x is an n-dimensional fea-
ture vector, the Min-Max normalisation is computed
by using the following linear interpretation formula:
x
′
= (x
i
− x
min
)/(x
max
− x
min
), (7)
where x
min
and x
max
represent the maximum and min-
imum values across all dimensions for each image
vector, x. The normalised Fisher vector, x
′
has the
same dimensionality as that of Fisher vector, x. The
Min-Max normalisation has the advantage of preserv-
ing exactly all relationships in the data. Results of
the normalisation scheme could be seen in Figure 1.
Conventionally, the recommended Fisher vectors for
large scale image retrieval are derived from Gaussian
mixture model (GMM) and deploy L2-normalisation
scheme to improve their classification performance
(Perronnin et al., 2010). We checked the L2 and
L1 normalisation techniques for deep Fisher vectors
but did not get as much improvement in discrimina-
tion performance as from the Min-Max normalisation
scheme.
4 COMPRESSION TECHNIQUES
In this section, we discuss the following off-the shelf
compression techniques used to reduce the dimen-
sions of normalised Fisher vectors: Principal compo-
nent analysis (PCA), Spectral Hashing (SH), Auto-
encoder and Parametric t-SNE.
4.1 Principal Component Analysis
(PCA)
Principal components analysis (PCA) (Pearson, 1901)
is a linear dimensionality reduction technique that
transforms d dimensional data set into a k dimen-
sional subspace (k < d) such that most of the infor-
mation in the data is retained. The transformed sub-
space, k denotes uncorrelated orthogonal dimensions
along which the data contains maximum variance and
its k-dimensional data representations are called prin-
cipal components or eigen vectors. Eigen vectors are
generally associated with an eigen value which are in-
terpreted as the ‘length’ or ‘magnitude’ of the corre-
sponding eigenvector. If some eigenvalues have a sig-
nificantly larger magnitude than others, then the di-
mensionality reduction of the data set onto a smaller
dimensional subspace is performed by dropping the
‘less informative’ eigen pairs.
Compression Techniques for Deep Fisher Vectors
219

4.2 Spectral Hashing (SH)
Spectral hashing (Weiss et al., 2009) is a non-linear
dimensionality reduction technique that minimises
the Hamming distance between similar pairs of binary
codes using a Gaussian kernel. The algorithm aims to
learn binary encodings of data in such a way that the
points distant in the Euclidean space are also distant in
the Hamming space and vice versa. Spectral hashing
calculates binary mappings by simply minimising the
sum of the Hamming distances between pairs of bi-
nary codes weighted by the Gaussian kernel between
the corresponding vectors. The compact binary code
solution is eventually obtained by thresholding a sub-
set of eigen vectors of the Laplacian of the similarity
graph.
4.3 Autoencoder
Autoencoder (Hinton and Salakhutdinov, 2006) is a
multi-layer stochastic neural network that uses both
encoding and decoding layers to yield non-linear pro-
jections of the data. The encoding layers of the net-
work transform high dimensional data into a low di-
mensional space, while the decoding layers of the net-
work recover the original data from compressed form
into its original input dimensionality. The unsuper-
vised learning algorithm trains both types of network
layers by minimizing the disparity between the orig-
inal data and its reconstructions using chain-rule to
calculate error derivatives for back propagation. In
autoencoder, a joint configuration (v, h)of the visible
and hidden units have the energy:
E(v,h) = −
∑
i∈pixels
b
i
v
i
−
∑
j∈ f eatures
b
j
h
j
−
∑
i, j
v
i
h
j
w
i, j
,
where w corresponds to the weight connections be-
tween the visible and hidden units and b
i
,b
j
corre-
spond to the biases connected to the visible and hid-
den units of the network.
4.4 Parametric t-SNE
Parametric t-SNE (Maaten, 2009) is an unsupervised
dimensionality reduction technique that preserves lo-
cal structure of the data in low dimensional space by
learning a parametric mapping, f : X → Y which uses
a feed-forward neural network with weights W be-
tween the high dimensional space X and low dimen-
sional space Y. The training procedure of paramet-
ric t-SNE is based on the following three steps: (1)
Training RBM (2) Construction of a pre-trained neu-
ral network using stack of RBMs and (3) Fine tuning
of the neural network using back-propagation such
that the cost function is minimised. The cost func-
tion of this network is a Kullback Leibler divergence
function showing divergence between the probabili-
ties reflecting the pairwise distance of data in the in-
put space and the latent space.
5 EXPERIMENTS
In order to evaluate the classification performance of
compressed Fisher vectors, we applied four differ-
ent compression schemes on Fisher vectors and cal-
culated their accuracies with a simple linear classi-
fier, i.e. k-nearest neighbour. The data set we have
taken for exploration is MNIST. The MNIST dataset
consists of 28× 28 dimensional images with 60,000
digits in the training set and 10,000 digits in the test
set. These images are vectorised to form a 784 di-
mensional vector fed to the RBM’s visible layer for
training.
5.1 Experimental Setup
To start with, we have performed classification ex-
periments on Fisher vectors derived from a compact
RBM with 1 and 5 hidden units. The FVs could
have also been derived from a very shallow model
containing thousands of hidden units as reported in
(Azim and Niranjan, 2013), however in that case the
dimensionality of the Fisher vectors scales to a mag-
nitude of 10
6
and the model tends to over-fit resulting
in no classification performance improvements. We
therefore constrained our compression experiment to
Fisher vectors derived from a small RBM that has
shown to report the best performance on MNIST. The
Fisher vectors derived from RBM with 1 hidden unit
havedimensionality 784. Similarly, the Fisher vectors
derived from RBM with 5 hidden units have dimen-
sionality 3920. Please note that we have skipped com-
puting Fisher scores using Equation 5 and Equation 6.
This is because these gradients were not found to im-
prove the classification accuracy of the system. Con-
sequently, we only used Equation 3 to compute the
Fisher scores. We compress these two kinds of Fisher
vectors using standard techniques such as PCA, spec-
tral hashing, autoencoder and parametric t-SNE. The
performance of these compression techniques is eval-
uated by plotting two-dimensional visualisations and
by measuring their overall classification performance
through linear classifier like k-nearest neighbour (k-
nn).
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
220

(a) Parametric t-SNE (b) Autoencoder
(c) PCA
Figure 2: Visualisation of compressed Fisher scores derived from 1 hidden unit RBM.
(a) Parametric t-SNE (b) Auto encoder
(c) PCA
Figure 3: Visualisation of compressed Fisher scores derived from 5 hidden units RBM.
6 RESULTS AND DISCUSSION
In Figure 2 and 3, we present the visualisation of
Fisher vectors compressed by PCA, auto-encoder and
parametric t-SNE. We have not shown the visualisa-
tion results of spectral hashing because it gives binary
codes that could not be compared with the remain-
ing visualisation schemes. The visualisations shown
Compression Techniques for Deep Fisher Vectors
221

Table 2: Accuracy of k-nn classifier on un-normalised Fisher scores derived from 1 unit RBM on MNIST data set.
Compression Techniques 2D 10D 20D k-nn
Parametric t-SNE 0.10% 0.10% 0.32%
0.960%
Autoencoder 0.098% 0.098% 0.098 %
PCA 0.099 % 0.18% 0.14%
Spectral Hashing 0.19% 0.099% 0.10%
(nbits=16) (nbits=80) (nbits=160)
Table 3: Accuracy of k-nn classifier on normalized Fisher scores derived from 1 unit RBM on MNIST data set.
Compression Techniques 2D 10D 20D k-nn
Parametric t-SNE 0.86% 0.94% 0.942%
0.960%
Auto encoder 0.78% 0.89% 0.96%
PCA 0.27% 0.67 % 0.68%
Spectral Hashing 0.66% 0.50% 0.44%
(nbits=16) (nbits=80) (nbits=160)
Table 4: Accuracy of k-nn classifier on normalized Fisher scores derived from 5 units RBM on MNIST data set.
Compression Techniques 2D 10D 20D k-nn
Parametric t-SNE 0.83% 0.93% 0.932%
0.963%
Autoencoder 0.75% 0.94% 0.96%
PCA 0.26% 0.68% 0.70%
Spectral Hashing 0.67% 0.43% 0.38%
(nbits=16) (nbits=80) (nbits=160)
are constructed by compressing the Fisher vectors ob-
tained from test images into two dimensions. In Table
2, we show the accuracy of k-nearest neighbour clas-
sifier on un-normalised Fisher vectors. Table 3 and 4
demonstrate the accuracy of k-nn classifier on Min-
Max normalised Fisher vectors derived from RBM
with 1 and 5 hidden units respectively. Our results re-
veal that Min-Max normalisation has a huge impact
on the classification accuracy achieved by compact
Fisher features.
From the deep Fisher vector classification results,
we observe that feature scaling matters largely when
using a Euclidian distance metric space as it is sensi-
tive to the differences in the magnitude or scale of the
attributes. Since k-nn uses Euclidian metric space, it
is important to normalise the derived Fisher features
so that it assigns an equal contribution to all the fea-
tures, prevents outweighing attributes and suppresses
the effect of outliers. Table 2 of our experiments
also give an insight that if the data is not normalized
in the range [0, 1], the sigmoid activation function
used in autoencoder and parametric t-SNE would sat-
urate the gradients of the sigmoid function leading to
very poor/no training of the networks. This ultimately
leads to poor classification results as shown in Table
2. Accuracy of k-nn classifier in Table 3 and 4 shows
that if all the features are on same scale then there is
no knock-on effect on the parameter learning of au-
toencoder and parametric t-SNE.
Our visualisations in Figure 2 and 3 show that
PCA does not preserve the significant structure of
data in low dimensional space. We therefore con-
clude the following for PCA: 1) PCA makes compu-
tation of eigen vectors infeasible for high dimensional
Fisher vectors (say of magnitude 10
6
) as the compu-
tation of covariance matrix becomes difficult, 2) PCA
is not scale-invariant and it mainly focuses on pre-
serving large pairwise distances instead of small pair-
wise distances which are important too. In contrast to
PCA, other compression techniques such as autoen-
coder and parametric t-SNE show much better dis-
criminative visualisations and thus yield better clas-
sification accuracies simultaneously. The best com-
pression performanceon deep Fisher vectors is shown
by parametric t-SNE as it preserves the local struc-
ture of the data appropriately in low dimensional sub-
space using heavy tailed student t- distribution. The
visualisations reflect Fisher scores in distinct clusters
representing their membership to different classes of
digits. In comparison to parametric t-SNE, the sec-
ond best classification and visualisation performance
is shown by autoencoder. When using spectral hash-
ing (SH), we observed that the performance of the
nearest neighbor classifier decreases as the number of
code bits increase. This is because in spectral hash-
ing, Euclidian distance is inversly proportional to the
Hamming affinity, thus when the number of bits ap-
proach to infinity, spectral hashing does not guarantee
to faithfully reproduce the affinity between the data.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
222

7 CONCLUSION & FUTURE
WORK
In this paper, we have applied different compression
techniques on Fisher vectors derived from restricted
Boltzmann machine to make them amenable for large
scale retrieval problems. We explored four different
dimensionality reduction techniques for Fisher vec-
tors: PCA, spectral hashing, parametric t-SNE and
autoencoder,and found that parametric t-SNE outper-
forms all the other techniques on high dimensional
Fisher vectors. Moreover, the Max-Min normalisa-
tion scheme improves the accuracy of the linear clas-
sifier in Euclidian space.
In the future, we would extend our experiments
to other large scale data sets like PASCAL-VOC (Ev-
eringham et al., 2015) and ImageNet (Russakovsky
et al., 2015) and test the classification performance of
compressed Fisher scores with other competitive clas-
sifiers like support vector machines (SVM). In addi-
tion, we shall also explore if feature selection meth-
ods are much apt than feature compression schemes
to reduce the dimensionality of deep Fisher vectors
for retrieval tasks.
ACKNOWLEDGEMENT
This research was supported by Higher Education
Commission of Pakistan (SRGP: 21-402) & NVIDIA
(Ref.: 281400) with a valuable donation of Titan-X
graphics card.
REFERENCES
Azim, T. and Niranjan, M. (2013). Inducing Discrimina-
tion in Biologically Inspired Models of Visual Scene
Recognition. In IEEE International Workshop on Ma-
chine Learning for Signal Processing (MLSP).
Boureau, Y., Bach, F., LeCun, Y., and Ponce, J. (2010).
Learning Mid-level Features for Recognition. In IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition.
Chatfield, K., Lempitsky, V., Vedaldi, A., and Zisserman, A.
(2011). The Devil is in the Details: An Evaluation of
Recent Feature Encoding Methods. In Proceedings of
the British Machine Vision Conference. BMVA Press.
Csurka, G., Dance, C., Fan, L., Willamowski, J., and Bray,
C. (2004). Visual Categorization with Bags of Key-
points. In Workshop on Statistical Learning in Com-
puter Vision, ECCV. Prague.
Everingham, M., Eslami, S., Van Gool, L., Williams, C.,
Winn, J., and Zisserman, A. (2015). The Pascal Visual
Object Classes Challenge: A Retrospective. Interna-
tional Journal of Computer Vision, 111(1):98–136.
Farquhar, J., Szedmak, S., Meng, H., and Shawe-Taylor, J.
(2005). Improving Bag-of-Keypoints Image Categori-
sation: Generative Models and PDF-Kernels.
Hinton, G. (2002). Training Products of Experts by Mini-
mizing Contrastive Divergence. Neural Computation,
14:1771–1800.
Hinton, G. (2010). A Practical Guide to Training Restricted
Boltzmann Machines. Technical report.
Hinton, G. and Salakhutdinov, R. (2006). Reducing the Di-
mensionality of Data with Neural Networks. Science.
Jaakkola, T. and Haussler, D. (1998). Exploiting Genera-
tive Models in Discriminative Classifiers. In Advances
in Neural Information Processing Systems 11, pages
487–493. MIT Press.
Jayalakshmi, T. and Santhakumaran, A. (2011). Statistical
Normalization and Back Propagation for Classifica-
tion. International Journal of Computer Theory and
Engineering.
Lazebnik, S., Schmid, C., and Ponce, J. (2006). Beyond
Bags of Features: Spatial Pyramid Matching for Rec-
ognizing Natural Scene Categories. In IEEE Com-
puter Society Conference on Computer Vision and
Pattern Recognition (CVPR’06). IEEE.
Maaten, L. (2009). Learning a Parametric Embedding by
Preserving Local Structure. RBM.
Maaten, L. (2011). Learning Discriminative Fisher Kernels.
In Getoor, L. and Scheffer, T., editors, Proceedings of
the 28th International Conference on Machine Learn-
ing, ICML 2011, Bellevue, Washington, USA, June 28
- July 2, 2011, pages 217–224. Omnipress.
Pearson, K. (1901). On Lines and Planes of Closest Fit to
Systems of Points in Space. Philosophical Magazine,
2:559–572.
Perronnin, F. and Dance, C. (2007). Fisher Kernels on Vi-
sual Vocabularies for Image Categorization. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion. IEEE.
Perronnin, F., Dance, C., Csurka, G., and Bressan, M.
(2006). Adapted Vocabularies for Generic Visual Cat-
egorization. Springer Berlin Heidelberg.
Perronnin, F. and Larlus, D. (2015). Fisher Vectors Meet
Neural Networks: A Hybrid Classification Architec-
ture. In Proceedings of the IEEE Conference on Com-
puter Vision and Pattern Recognition. CVPR.
Perronnin, F., S´anchez, J., and Mensink, T. (2010). Improv-
ing the Fisher Kernel for Large-scale Image Classifi-
cation. In European Conference on Computer Vision.
Springer.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh,
S., Sean, M., Zhiheng, H., Karpathy, A., Khosla, A.,
Bernstein, M., Berg, A., and Fei-Fei, L. (2015). Im-
ageNet Large Scale Visual Recognition Challenge.
International Journal of Computer Vision (IJCV),
115(3):211–252.
Sanchez, J., Perronnin, F., Mensink, T., and Verbeek, J.
(2013). Compressed Fisher Vectors for Large-scale
Image Classification. IJCV.
Wang, J., Yang, J., Yu, K., Lv, F., Huang, T., and Gong, Y.
(2010). Locality-constrained Linear Coding for Im-
Compression Techniques for Deep Fisher Vectors
223

age Classification. In IEEE Conference on Computer
Vision and Pattern Recognition (CVPR). IEEE.
Weiss, Y., Torralba, A., and Fergus, R. (2009). Spectral
Hashing. In Advances in Neural Information Process-
ing Systems. NIPS.
Zhang, Y., Wu, J., and Cai, J. (2014). Compact Repre-
sentation for Image Classification: To Choose or to
Compress? In Proceedings of the IEEE Conference
on Computer Vision and Pattern Recognition. IEEE
Computer Society.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
224