Impact of Machine Reliability on Key Lean Performance Measures:

The Case of a Flexible Manufacturing System (FMS)

Wa-Muzemba Anselm Tshibangu

Department of Industrial and Systems Engineering, Morgan State University, 1701 E Cold Spring Lane,

Baltimore, MD 21251, U.S.A.

Keywords: Little’s Law, Simulation, Lean Six Sigma, Throughput, Mean Flow Time, Work in Process, Reliability,

MTBF, MTTR.

Abstract: Uncertainty in production systems may arise from different sources including machines, parts, tools or

material handling failures. For this reason the need for the production system to be flexible enough to

respond to unanticipated breakdowns or failures become highly recognized. This paper considers a flexible

manufacturing system (FMS) and analyzes the effect of a combination of various design and operational

parameters on the overall system performance under different machine failures/breakdowns patterns. Three

performance criteria including throughput rate (TR), mean flow time (MFT), work-in-process (WIP), are

analyzed for various machine and AGV scheduling rule combinations over a range of AGV fleet size. These

key Lean indicators are selected because they are tenants of Little’s Law considered as the backbone

equation in Lean Six Sigma methodologies as it advocates the reduction of waste, variability and work in

process around the process in order to reduce the cycle time while increasing quality. Comparison is made

with the performance profile of a system operating in a failure-free mode. The results reveal that machine

and material handling scheduling rule combinations together with the maintenance policy in use may affect

significantly the performance of a production system. The results also show that there is an acceptable level

of machine breakdown (reliability) for which the system performance is similar to a failure free system.

1 INTRODUCTION

Manufacturers and service providers usually need to

deal with a certain number of uncontrollable factors

including variations in input part arrival rate,

probability distribution of the input part type, failure

rate of machines, and rework rate of parts after

inspection, etc. (Tshibangu 2006). Because a

characteristic of demand in a modern economy is

small quantity and high variety of products and or

services, the effects of variations due to these

uncontrollable factors can be drastic. In order to face

increasing global competition manufacturing and

production systems operate with small batches and

high variability of products and or services in

conditions similar to that of a flexible manufacturing

system (FMS). During the operation of such highly

integrated and automation driven facilities (e.g.,

FMS) various components can fail due to different

reasons. The failure of a single component may

force a very expensive machine to idle, and, because

there is limited work-in-process (WIP) within the

system boundary, the entire system can be brought

to starvation or stoppage. Therefore, in these

potentially disruptive environments reliability-

related issues become important because of their

possible negative effect on the overall system

performance. It has been demonstrated that for an

FMS with a given performance reliability, operating

policies for the scheduling decisions also affect the

performance of the system (Sridharan, 2000).

Many analytical tools exist to address these

issues with simulation being one of the most

powerful and extensively used, particularly for

design (Ball and Love, 2009). This is the reason why

this study uses simulation experiments on a flexible

manufacturing system (FMS) to study the effect of

machine reliability on the overall performance of the

system. The research investigates the effect of

scheduling decisions on FMS performances under

various machine failure scenarios. The scheduling

decisions studied in this research include the number

of automated guided vehicles AGVs, the queue

discipline, and the AGV dispatching rules.

Tshibangu, W-M.

Impact of Machine Reliability on Key Lean Performance Measures: The Case of a Flexible Manufacturing System (FMS).

DOI: 10.5220/0005986705670575

In Proceedings of the 13th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2016) - Volume 2, pages 567-575

ISBN: 978-989-758-198-4

567

2 MOTIVATION

At present, there is little research available on the

effect of FMS reliability on the overall performance

of the system. It has been shown that for an FMS

with a given performance reliability, operating

policies for the scheduling decisions also affect the

performance of the system (Sridharan, 2000).

However, during the FMS operation, some

disturbances, such as machine and/or AGV

breakdowns, maintenance operations, poor tool

management, may drastically affect the FMS

performance. Depending on the breakdowns

occurrence (frequency) and the length of the repair

(criticality), the system performances such as

throughput time of parts, completion time of parts,

machines and AGVs utilization may deteriorate

significantly. Thus, it is necessary to include the

breakdown aspect of disturbances for a realistic

evaluation of FMS performances.

This research particularly deals with machine

breakdowns and repair in an FMS. Although AGV

system is considered as the backbone component of

an FMS, AGV breakdown is not considered because

the author believes that an AGV is such a critical

component to an FMS that a wise management

decision may consist in investing in redundancy than

incurring loss because of unpredicted unavailability

of the equipment.

3 RESEARCH PROBLEM

The research problem addressed in this study is to

analyze the effect of combination of a pairwise

machine and AGV dispatching rules with a design

problem such as number of vehicles on the

performances of an FMS operating under various

patterns of machine breakdowns. The results are

compared to the same FMS configuration under a

failure-free operating mode.

4 DECISION LEVELS IN FMS

Decision making problems in FMSs are made at

three levels, namely: i) the design level, which deals

with long-term decisions, such as the selection and

layout of machine tools and the material handling

system; ii) the planning level which addresses

medium-term resource allocation decisions, such as

assigning operations and cutting tools to machines,

and iii) the scheduling level, which considers the

execution of orders in the short term, and includes

determining the sequence for processing various

parts on each machine.

4.1 Design-related Problems

Design related problems encompass many aspects

including: i) part types to be produced; ii) process

plan including tooling and tool magazine; iii) type

and capacity of material handling systems; iv) fleet

size (number of vehicles needed); v) speed of

material handling devices; vi) inter-arrival time; vii)

type and size of buffers. Buffers provide queuing

spaces for in-process inventory (In this paper, the

buffer size is considered fixed with a capacity of 10

parts).

4.2 Operational Control Related

Problems

The ability of a manufacturing system to operate in

accordance with the promised potentials depends

heavily on the operational control in force. The

dispatching mechanism controls the flow of material

in the manufacturing system and determines the

release and transfer of jobs (parts) between

workstations. Dispatching rules are either machine-

or material handling-related. Tshibangu (2012)

shows that there is a two-way interaction between

machines and AGVs, and indicates that due to this

two-way interaction, a realistic analysis of AGV-

served manufacturing systems needs to coordinate

both machine and AGV operations.

Therefore, during shop operation, a good

dispatching policy should be integrated to the design

state to maximize the overall system performance. It

is important to note that these scheduling decisions

may be jeopardized by the failure of machines. In

this research the number of vehicles is varied in

order to determine whether or not the increase of

fleet size may be a remedial solution to prolonged

breakdowns.

5 UNCERTAINTY:

ASSUMPTIONS AND

CHARACTERIZATION

This research considers and analyzes the type of

uncertainty related to machine breakdown rates. A

flexible manufacturing system (FMS) is analyzed in

order to evaluate the nature, form and extent of

different machine breakdown rates. Uncertainty in

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

568

this research is characterized by machine mean time

to failure (MTBF). The breakdowns and the

maintenance operations are highly machine

dependent. Therefore, individual machines would

normally have their own reliability and maintenance

requirements.

Although a production environment in reality

contains a variety of general-purpose and dedicated

machines capable of performing various operations,

this study assumes the same reliability for all

equipment, that is, all machines have the same

MTBF. Machine downtime, characterized by the

mean time to repair (MTTR) is a measure of the

severity of the breakdown. This characteristic is

integrated in this research though not fully

investigated. For reasons of simplicity, machine

downtimes are assumed to be constant for all the

machining centers, that is, the MTTR for all

processing centers is identical and has the same

value for all breakdown occurrences.

The FMS studied operates for 3 consecutive

shifts of 8 hours. Machine mean time between

failures (MTTBF) are assumed to be exponentially

distributed with means varying from 150 minutes to

30 minutes, and the MTTR is also considered to be

exponentially distributed with a constant mean of 10

minutes for all failure occurrences. It is assumed that

the reliability function

)(tR , defined as the

probability of no failure for the machine during the

time interval

),0( t , is given by:

[]

ttR

−= exp)(

(1)

where

is a constant hazard rate, and

the time.

The results of a system prone to failure are

compared with the same FMS configuration with no

machine failures for operation time of 30 minutes.

The time range of 30 minutes has been considered

this research to include the highest probable

processing time.

6 LITERATURE REVIEW

Sridharan and Babu (1998) use a detailed simulation

study on a typical FMS under two situations: (1) the

FMS is failure free; (2) the FMS is prone to failures.

They develop metamodels for the two types of

FMSs. The metamodels have been found to be

useful for simulating the studied FMSs and for

evaluating various multi-level scheduling decisions

in the FMS. Sridharan et al. (2000) extend their

work and investigate the effects of a multi-level

decisions in a failure prone FMS. Six failure-repair

situations are considered, characterized by the

severity of failure frequency and the length of repair

time for machines and AGVs in an FMS Renna, P.

and Ambrico, M. (2011) examine cycle time and

WIP in a cellular manufacturing subject to dynamic

changes. Wassi Sorro et al. (2012) examine a system

in any of three states: nominal operating state,

degraded state or failure state. The system state is

known only after inspection. A maintenance action

is undertaken when at a predetermined instant an

inspection reveals that the system is in degraded or

failure state. The maintenance action restores the

system to its nominal operating mode with a certain

probability. A periodic type inspection strategy is

used and proposed. In all the studies mentioned

above design and operational categories were

pursued separately. As an innovation this research

study integrates issues from both groups and

investigates the effects of machine failure rate (or

machine reliability) and AGV dispatching rules as

operational variables while considering AGV fleet

size as the design variable in studying FMS

performances.

7 RESEARCH APPROACH

Two heuristics for vehicle-initiated dispatching have

been selected in this study: i) the first come first

serve (FCFS) dispatching rule assigns vehicle to

demands sequentially as requests for AGVs are

received from different machines; ii) the shortest

traveling distance (STD) rule minimizes the time

vehicle travels empty. This rule dispatches the

released vehicle to the machine which is closest to

the idle vehicle. The machine dispatching rules

(queue discipline) considered in this study include:

(1) the short processing time (SPT) rule that

dispatches the job with the smallest processing time

and the first in first out (FIFO) rule that dispatches

jobs sequentially on the machine as the previous part

in the queue has been completed. This leads to 2

sets of dispatching rules combinations to be

analyzed, i.e., FIFO/SDT, FIFO/FCFS, SPT/SDT,

SPT/FCFS. The first acronym stands for the queue

discipline (machine scheduling) rule in use, while

the second design the AGV dispatching rule.

For each of these machine and AGV dispatching

rule combination, 5 failure-repair configurations are

examined to evaluate the FMS performance under 5

situations, each one involving a different number of

vehicles. This combination results into a total of 100

Impact of Machine Reliability on Key Lean Performance Measures: The Case of a Flexible Manufacturing System (FMS)

569

simulation experiments to be performed under

various machine breakdowns.

In addition, for each number of vehicles studied

in this research, simulation runs are also carried out

on the same FMS configuration under no failures.

This implies 20 additional simulation runs for the

failure-free situation leading to a total of 120 of

simulation experiments. The results from the failure

free situation are subsequently compared with those

from the FMS prone to failure in the analysis.

8 THE SHOP MODEL

The hypothetical FMS layout used in this paper is

similar to the one used by Tshibangu (2003, 2012).

The job shop model is composed of nine

workstations, including a loading or receiving

station (workstation 1) and an unloading or shipping

station (workstation 9).

8.1 Job Descriptions

All jobs enter the system through the receiving

department and leave the shop through the shipping

department. It is assumed that raw materials are

always available at the loading station and parts that

arrive at the unloading station depart the system

immediately after being unloaded. Each job consists

of only one unit load and is processed and moved

between work stations as a single unit load. AGV

carts move parts between the workstations along a

predetermined mixture of uni- and bi-directional

paths.

8.2 Simulation Model

Jobs are simulated to arrive at random times for the

entire operational period following a Poisson model

because this distribution provides a good

approximation for the job arrival when generating

sources are assumed to be independent. For each

experimental condition the simulation is run with

three independently-seeded replications of 600

minutes each. The first 120 minutes of each run are

truncated to eliminate the initial bias. The remaining

480 minutes representing an operational shift of 8

hours are replicated three times to represent each

daily shift, and the outputs from the three

replications are collected and averaged out across

replications. To simulate a fairy busy system, the

arrival rate of jobs is assumed to be equal to the ratio

of the capacity of the job shop to the average amount

of work required. The arrival rate, denoted by

, is

then given as:

(2)

where

M = number of machines

η= machine load capacity

n = average number of operations

= average operation times

Following this model, various arrival patterns can be

obtained by adjusting the machine load capacity

factor

. Changing the arrival rate gives the

experimenter the flexibility to control the degree of

congestion in the shop. In this research, a machine

load capacity of 90%

)90.0( =

was assumed in

generating the job arrival process. The jobs were

simulated to have one to 7 different types of

operations, the number being assigned randomly

using a uniform distribution

)7,1(U

. The average

number of operations is

4=n

. The average

operation time of 15 minutes is also extracted from a

uniform distribution model

)25,5(U

. Using Eqn.

(2), a value of the arrival rate

135.0=

has been

used.

8.3 FMS Configuration

The FMS configuration studied is summarized in

Table 1. There are 15 parts types in total, and all the

processing times are assumed to be known

deterministically, since all the machining operations

are computer numerically controlled. Besides, all the

raw materials are assumed to arrive at time zero.

Two different simulation models have been

developed, one for failures free machines failures,

and another for machines prone to failures. The

simulation experiments have been carried out for 4

different combinations of machine and AGV

dispatching rules as operational control input

parameters, with various numbers of vehicles as a

design input parameter. Three performance

measures are evaluated for each configuration and

later compared for further insights and conclusions.

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

570

Table 1: Shop Configuration.

Part Types considered

for production

Machines 9 (including one

loading and one

unloading stations)

Material Handling

Systems (AGVs)

Variable from 3 to

Buffer Capacity 10 for workstations 2

to 8

Infinite for

workstation 1

Loading/Receiving

stations

1 (workstation 1)

Unloading/Shipping

stations

1 (workstation 9)

8.4 Shop Conditions and Assumptions

A number of simplifying assumptions have been

used for the simulation model, e.g., an AGV

transfers only one unit load at a time; pickup and

drop-off times of a part are set at a constant of 0.25

minutes each; machine failures are time-based

failures; the failure of resource (i.e., machine) will

occur at different rates taken from an exponential

distribution with a certain mean, e.g., EXPO (150);

breakdowns of vehicles (AGVs) are not considered,

etc. The reader is referred to Tshibangu 2006 for a

complete list of all the assumptions used in this

study.

8.5 Performance Evaluation

Three performance measures are used in this study

including i) system throughput per shift (TR); ii)

flow time (cycle time) MFT and iii) number of parts

in the system or work in process (WIP). These key

indicators are consistent with Little’s Law known

the governing equation of Lean Six Sigma

methodology as it evaluates the MFT as the ratio of

WIP to TR. The definitions and formulas of these

measures are provided in the equations below. All

quantities are mean values averaged across the three

replications.

(1) Mean Throughput Rate (MTR), here defined as

the total number of parts (all types confounded)

during a shift. If

,...2,1=

is the number of

type

i parts produced during a shift, then:

MTR =

∑

parts/min (3)

(2) Mean Flow time (MFT), also known as cycle

time for a part

is defined as the time

elapsed between its arrival and its departure.

Thus, it is the sum of part’s delay in queues and

its service time. When there are more than one

entity (part) in the model, the total flow time

will include the sum of all flow times (

∑

The mean Flow Time in this study is computed

as follows:

∑

MFT

(4)

(3) Average number of parts in shop, also called

work-in-process (WIP) is a time-persistent

measure and represents the total number of all

part types present in the system in average

during the simulation time. In this research

study, WIP is computed as follows:

)

480

(

WIP ∗=

∑

(5)

9 RESULTS AND ANALYSIS

For each set of machine and AGV dispatching rules,

3 operational shifts of 480 minutes were simulated

with different material handling fleet size and under

different machine reliabilities (or different failure

rates). The simulation results are presented in

separate groups according to the machine/AGV rule

combination used or each performance measure.

Results of the simulation experiments for all

combinations of machine and AGV rules and

number of vehicles are not displayed in this paper

but they may be available upon request.

To answer the research question on whether or

not the combination of sets of machine/AGV

dispatching policies with number of AGVs in a

manufacturing or production environment with

machines prone to various failure rates has an

impact on the performance measures such

throughput rate, mean flow time, and work-in-

process, graphs are plotted and ANOVA models

developed. The data analysis section of this paper is

broken into three sections, one for each dependent

Impact of Machine Reliability on Key Lean Performance Measures: The Case of a Flexible Manufacturing System (FMS)

571

variable (performance measure), and for each

performance measure the effect of fleet size and

machine reliability will be analyzed.

9.1 Throughput Rate

The results of data analysis confirm the author’s

prior knowledge about the impact of number of

vehicles present in a system. Tshibangu (2006)

reported that the throughput behaves in a concave

manner with respect to the AGV fleet size. The

objective in determining the optimal fleet size is to

have the smallest number of vehicles in the system,

but still capable to achieve the performance

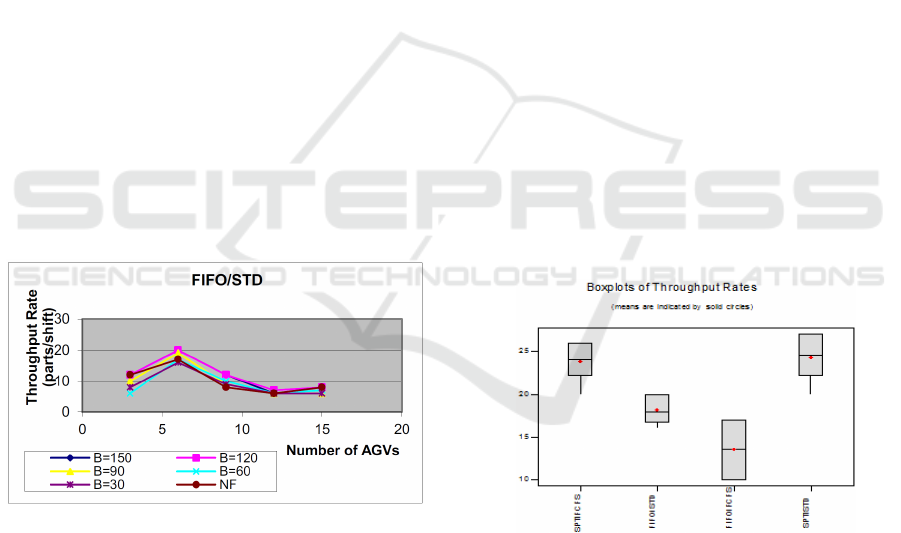
requirements. For illustration purpose Figure 1

depicts just the throughput rate TR for SPT/SDT

machine /AGV combination rules.

As the number of vehicles increases in the

system the throughput rate increases due to material

flow capacity. However, beyond a certain number of

vehicles, an addition of more vehicles results in

increasing traffic congestion and blocking of

vehicles leading to a decrease in the throughput rate

as a result of the delay caused to AGVs in

completing their tasks. As noted in Tshibangu

(2006) this is both economical and operational

waste. The highest throughput rate for all rule

combinations is observed with the configuration free

of failures, i.e., machine reliability =100%.

Figure 1: Average (WIP) under Machine SPT and AGV

FCFS.

For a value of MTBF = EXPO (150) minutes or a

machine failure rate λ = 0.0067 per minute

equivalent to a half hour reliability of 82 %, the

system behaves exactly like the zero-failure

configuration.

The reliability is calculated on a 30 minutes time

frame in order to be as close as possible to the

longest possible processing time used in this

research as they are generated from a uniform

distribution

)25,5(U . It can be noticed that the

system TR performance starts to degrade when

failure rates reach values higher than 0.0067 min

-1

i.e., for MTBF values less than 150.

In other words, the company production

management board can ensure a good performance

of the system by implementing maintenance policies

that can keep the reliability of the resources

(machines) at a level that will allow the FMS to

behave as a failure-free system. A failure rate of

0.0067 min

-1

or less (i.e., half-hour machine

reliability of 82% or more) may be considered as

good enough to keep the throughput rate at almost

the same level as in a system free of failures.

A widely adopted philosophy in determining the

optimum AGV fleet size recommends the optimum

number of vehicles to be the one that maximizes the

throughput TR of the system. Analysis of the

various output graphs along with pilot simulation

runs revealed that the maximum number of vehicles

needed in the system under study in this research is

equal to six (6) for all set of machine and AGV

scheduling rule combinations.

To test the relative performance of different set of

combinations of machine and AGV rules with respect

to the throughput rates TR, a one-way ANOVA has

been developed but the results are not presented in

this paper for space compliance. However, the

associated boxplots represented in Figure 2 reveal a

significant difference between the performances of

the 4 sets of combined machine/AGV rules tested.

Figure 2: Relative Performance of Sets of Rules on TR.

The highest throughput is achieved by both

SPT/STD and SPT/FCFS, with a slight difference in

favor of SPT/STD. This means that the best queue

discipline is SPT, regardless the AGV dispatching

rule associated with. Results also suggest that FIFO

is the worst queue discipline rule, independently of

the AGV rule used along with. Poor performance of

FIFO/FCFS is not a surprise because these two rules

give respectively priority to the first part in the

queue, or the first AGV available, without any

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

572

considerations about the part attributes (e.g.

processing time) or distance to be traveled to satisfy

a transportation request.

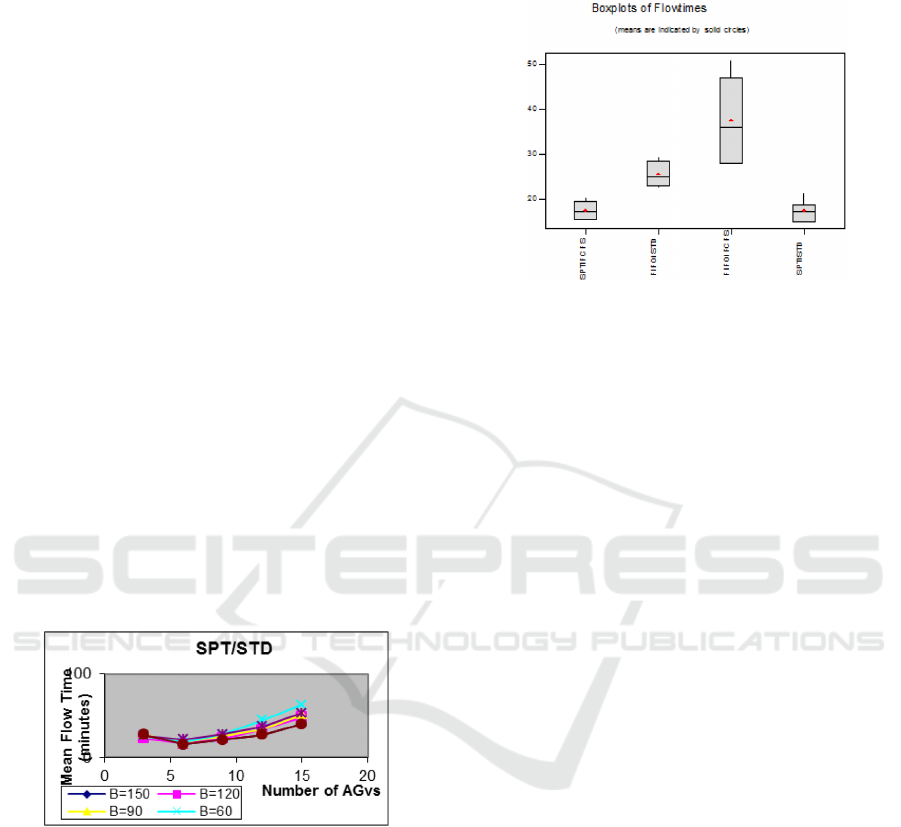
9.2 Mean Flow Time

The mean flow time performances of various

configurations of the system under study for

different levels of machine reliabilities have been

analyzed. Figure 3 depicts the MFT for STP/FCFS

for illustration purposes while the rest of the graphs

at other machine/AGV combination rules can be

obtained upon request. Observation of the various

graphs and plots produced with the study leads to the

conclusion that the mean flow times of a system

prone to machine failure follows the same almost

convex ascendant shape with regard to the fleet size.

When considering the variances on flow times, it

can be observed from the results that mean and

variances of the flow times are correlated, that is a

scheduling combination rules with larger mean flow

time value, also depict a lager variance, with the

only exception for the SPT/SDT.

The mean flow time is moderate when the

number of vehicles in the system is low, and

decreases to a minimum as this number is increased

because of the additional material flow capacity.

However, the addition of more vehicles results in an

increased congestion a higher mean flow time.

Figure 3: Average MFT under Machine SPT and AGV

FCFS.

Therefore, too many vehicles in the system

results in an increase of the mean flow time. The

number of AGVs that minimizes the system’s mean

flow time is also found to be equal to six.

To answer the research question with regard to the

relative performance of machine and AGV scheduling

rule combinations with respect to the mean flow time

ANOVA model and associated boxplots were

developed. The ANOVA results are not displayed in

this paper but can be obtained upon request. However,

analysis of boxplots displayed in Figure 4 reveals a

significant difference between the performances of

various combinations of operational rules.

Figure 4: Relative Performance of Sets of Rules (WIP).

SPT/STD and SPT/FCFS are the best achievers

with a slight difference in favor of the SPT/STD. But

SPT/FCFS has the least variance. A glance on

different mean flow time charts (not displayed in this

paper) reveals that in all situations, the zero-failure

configuration performs better than a system subject to

breakdowns. The effect of breakdowns is proportional

to the failure rate, i.e., the higher the machine failure

rate (or the lower the machine reliability), the higher

the system the mean flow time, and the lower the

machine failure rate (high reliability), the lower the

system mean flow time. Also, when the mean flow

time of the system is used as performance measure,

information from the part is more important than the

distance of the requesting part from the available

transportation device. FIFO/FCFS and FIFO/STD did

not perform well, with FIFO/FCFS being the worst

case. This again suggests that FIFO is not the best

machine scheduling rule when a system is assessed

with regard to the mean flow time.

9.3 Average Number of Parts in the

System (WIP)

The average number of parts in the system also

known as the work-in-process (WIP) behaves as

illustrated in Figure 5. The simulation results (not

displayed in this paper) along with the associated

graphs reveal that the fleet size has no effect on the

work-in-process. This almost agrees with Little Law’s

also known as the first law of manufacturing systems.

This law, which is perhaps the most recognized

working principle of production and manufacturing

systems and also used extensively today in Lean Six

Sigma states that: Work-in-process equals to the

production rate times the throughput time.

Impact of Machine Reliability on Key Lean Performance Measures: The Case of a Flexible Manufacturing System (FMS)

573

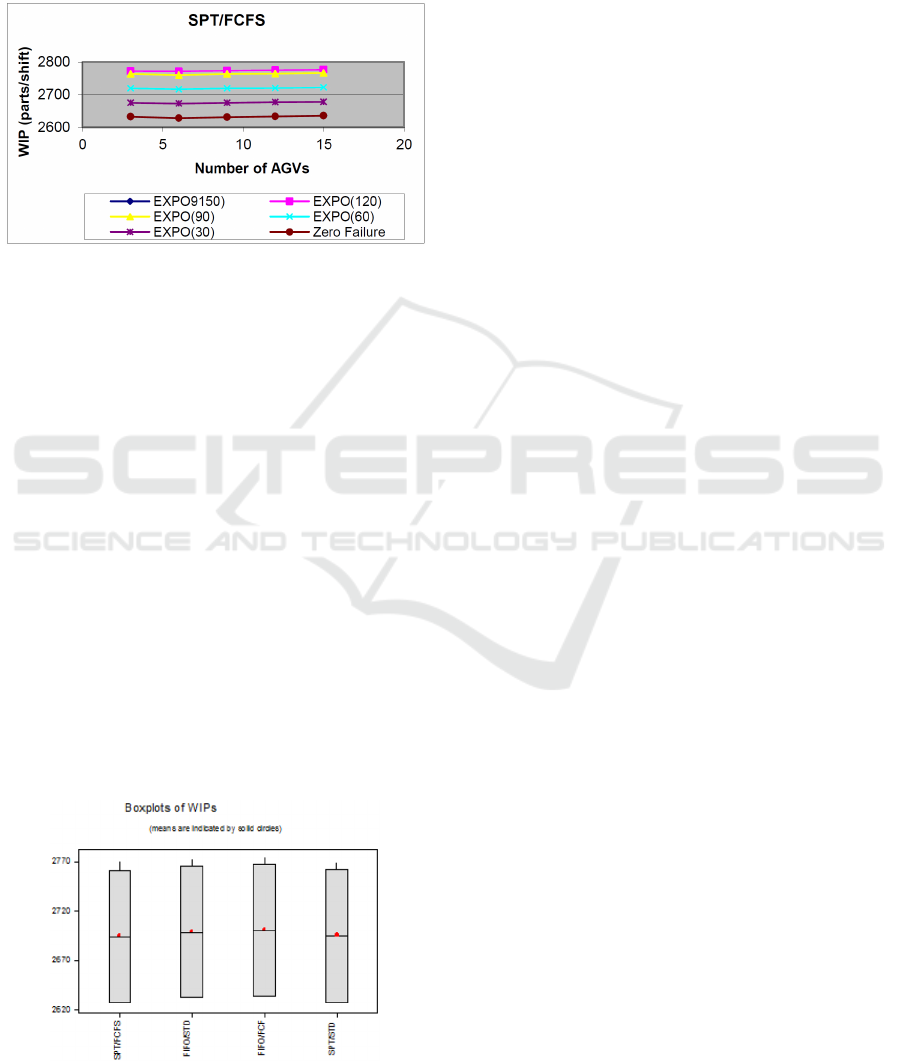
As pointed out earlier in this paper, the production

rate (also known as throughput rate) first increases

with the number of vehicles in the system until an

optimum fleet size is reached, and then starts to

decrease as more vehicles are added in the system.

WIP = Production Rate x Throughput Time (6)

Figure 5: Average (WIP) under SPT and FCFS Rules.

The throughput time (represented by the flow

time) behaves in the opposite way, i.e., first, an early

decrease is observed when the number of vehicles is

augmented, second, a minimum value is reached,

and third an increase is observed as more vehicles

are added. The two terms in Equation (6) acting in

opposition, their product might tend to be constant.

This would explain why WIP is not sensitive to the

fleet size.

However, the effect of failure rates (or machine

reliability) affects the system as expected. The

lowest WIP values are observed for the zero-failure

configuration for all machine and AGV scheduling

rule combinations. Then, as the failure rate of the

machines increases (reliability decreases), the WIP

increases. To determine the relative performance and

the significance of different machine and AGV

dispatching rule combinations on the work-in-

process (WIP) performance, a one-way ANOVA

model is developed and the different data plotted in

boxplots as shown in Figure 6.

Figure 6: Relative Performance of Sets of Rules on WIP.

The difference between the highest and lowest

WIPs observed for all machine and AGV scheduling

combinations are not really significant, and represent

less than 5% of the average number of parts in the

system. The comparison is conducted under a

configuration system with 6 AGVs, previously

identified as the optimum fleet size.

Detailed analysis of ANOVA results associated

plots of means reveals that statistically there is no

significant difference between the work-in-process

performances of all machine/AGV scheduling rule

combinations tested. The variances for different set

of rules were also found to be identical, suggesting

that the machine and AGV scheduling policy

combination does not seem to have significant

effects on system performance in terms of work-in-

process under the conditions of the present study.

However, this performance measure seems to be

more sensitive to part arrival rates and buffer size as

revealed by earlier pilot simulation runs.

10 CONCLUSIONS AND

FURTHER RESEARCH

This paper has extended the machine reliability

problem into machine and AGV scheduling issues in

flexible manufacturing settings.. System parameters

including the number of vehicles in the system,

machine and AGV scheduling rule combinations

were varied in simulation runs to allow a logical and

fair assessment of system performance measures.

Three performance criteria including throughput rate

(TR), mean flow time (MFT) and average work-in-

process (WIP) are tested in this research to

determine the effect of machine reliability (through

failure rate), fleet size (through the number of

vehicles in the system), and scheduling rules

(through machine and AGV scheduling rule

combinations). The results are then compared to the

same system configuration when operating failure-

free mode. The relative performance of a particular

set of operational rules is determined through

ANOVA procedures, pairwise tests on means,

boxplots, and scattered charts. A system free of

failures has been identified as the configuration that

gives the best results as compared to a system prone

to machine failures. Machine breakdowns have been

found to have a significant impact on the FMS

performances for failure rates larger than 18%, i.e., a

good preventive maintenance policy that can keep

the machine half-hour reliability of machines

ICINCO 2016 - 13th International Conference on Informatics in Control, Automation and Robotics

574

beyond 82% is a guaranty for good performance of

the system.

Results reveal that throughput rate and mean

flow time can be described as a concave, and a

convex function respectively, i.e., each reaches its

optimum (max for throughput, and min for mean

flow time) subject to both trends, the additional flow

capacity and the reduction in flow due to congestion.

This suggests that for both economical and

operational interests best results will be obtained by

operating the FMS with only the maximum number

of vehicles needed in the system. The average work-

in-process seems to be only slightly affected by the

fleet size. With the throughput and the flow time

behaving in opposite directions over the variation of

the fleet size, this result seems to comply with

Little’s law. Selection of particular operational plan,

i.e., machine and AGV scheduling rule combination

has been found to have a significant impact on all

the FMS performances studied in this research with

the exception of the work-in-process that seems to

be insensitive to operational rules in use. However,

pilot simulation runs have revealed that although the

combination of machine and AGV scheduling

policies did not seem to have significant effects of

the average number of parts in the system (WIP),

this performance value is highly affected part arrival

rate and buffer size, i.e., WIP is more sensitive to

part-related attributes than to the operational and

control issues in force. Simulation results have

shown that machine and AGV operational rules

combinations that outperformed with respect to

system throughput rate and mean flow time are

SPT/FCFS and SPT/STD, suggesting that a

combination of operational rules that includes part

information as queue discipline might be the better

achievers. The conclusions drawn in this research

may be completed by further investigation that may

include scheduling rules that consider other

attributes, such as part waiting time, length of queue

in front of a machine, severity of breakdowns

(various MTTR), and the number of part types.

REFERENCES

Ball, P.and Love, D., 2009. Instructions in Certainty,

Institute of Industrial Technology, 29-33.

Renna, P. and Ambrico, M. 2011. Evaluation of Cellular

Manufacturing Configurations in Dynamic Conditions

using simulation: International Journal Advanced

Manufacturing. Technology (2011) 56:1235–1251.

Sridharan, R. and Babu, A.S., 1998, Multi-level

scheduling decisions in a class of FMS using

simulation based metamodels, Journal of the

Operational Research Society, 49, 591-602.

Sridharan, R., Vishnu, A.S., and Babu, A. S., 2000,

Effects of multi-level scheduling policies in a failure

prone FMS: A simulation study. Journal of the

Operational Research Society.

Tshibangu, WM Anselm, 2013. A Two-Step Empirical-

Analytical Optimization Scheme, A DOE-Simulation

Meta-Modeling Approach, 10

International

Conference on Informatics in Controls, Automation

and Robotics.

Tshibangu, WM. Anselm, 2006 Robust Design of a

Flexible Manufacturing Systems: A Simulation

Metamodeling Approach, Proceedings of the 2006

Global Congress on Manufacturing and Management

(GCMM’2006), COPEC – Council of Researches in

Education and Sciences, Nov 19-22, Santos, Brazil.

Tshibangu, WM Ans elm. 2012: Lean, Six sigma,

Simulation, and DOE: An Framework to Optimal

Design and Implementation of a Cellular

Manufacturing, A Case Study, Proceedings of the 9

International Conference on Informatics in Control,

Automation and Robotics (ICINCO 2012), July 27-31,

2012 Rome, Italy.

Wassy Soro et. al 2010. Production Rate Maximization of

a Multi-State System Under Inspection and Repair

Policy, International Journal of Performability

Engineering Vol.8, No. 4, July 2012, pp. 409-416.

Impact of Machine Reliability on Key Lean Performance Measures: The Case of a Flexible Manufacturing System (FMS)

575