Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert

Huang Transform

Fabiola M. Villalobos-Castaldi

, José Ruiz-Pinales

, Nicolás C. Kemper-Valverde

Mercedes Flores-Flores

, Laura G. Ramírez-Sánchez

and Metztli G. Ortiz-Hernández

Centro de Ciencias Aplicadas y Desarrollo Tecnológico, UNAM, Expert Systems Lab,

Circuito Exterior S/N C.P. 04510, Ciudad Universitaria, Ciudad de México, D.F., Mexico

Electronics Engineering Department, Engineering Division, Universidad de Guanajuato

Carretera Salamanca - Valle de Santiago Km. 3.5 + 1.8. Comunidad de Palo Blanco Salamanca,

Leon, Gto., C.P. 36885, Mexico

Tecnológico de Estudios Superiores de Ecatepec, Av. Tecnológico S/N, Valle de Anahuac, C.P. 55210,

Ecatepec de Morelos, Mexico

Keywords: Time-frequency Analysis, Hilbert Huang Transform, Spontaneous Pupillary Oscillation, Non-traditional

Time-series Characterization Scheme.

Abstract: This paper proposes a new application of the Hilbert-Huang transform (HHT). Pupillogram recordings were

analyzed through the non-traditional HHT to investigate patterns in the time-frequency parameters of

Spontaneous Pupillary Oscillation (SPO) signals. The traditional Fourier transform is only useful for linear

stationary signals analysis, but the HHT was designed for the analysis of non-linear and non-stationary

signals. However, the HHT is a more suitable tool to study SPO signals which are fundamentally non-

stationary. The intrinsic properties of the Spontaneous Pupillary Oscillation signals were highlighted by the

HHT scheme and the results showed that SPO waves present local and intermittent variations through the

time span. The numerical parameters demonstrated that it is a wide inter-subject variation in the intrinsic time-

frequency parameters contribution from each yielding mode to the total signal content.

1 INTRODUCTION

This study proves the assumption that spontaneous

pupillary fluctuation is stationary can be a serious

misconception. Complex interactions exist between

the sympathetic and para-sympathetic systems which

are two components of the ANS autonomic nervous

system acting as a balance between competing neural

mechanisms. Using selected stimulations, the

dynamics of this balance mechanism could be

significantly altered. Such modifications can be

studied using relevant autonomic indices (De Souza,

et al., 2007).

The iris is a vascular structure and changes in

pupil size are controlled by two smooth muscles in the

iris (Sylvain and Brisson, 2014). The sphincter

pupillae located in the stromal layer is under

cholinergic control, mediated via para-sympathetic

nerves from the Edinger-Westphal nucleus. The

dilated pupillae situated posterior to the constrictor

muscle is innervated by adrenergic fibers originating

in the superior sympathetic ganglion. This set of

opposing muscles exercise a fine but extensive

control over the pupil (Newman, 2008).

The constriction and dilatation of the pupillary

aperture is produced mainly through ANS control

exerted on the muscles of the iris. More specifically,

neurons of the PSN innervate circular fibers of the

iris, causing pupillary constriction, whereas

excitation by SNS neurons causes the radial fibers of

the iris to produce dilation of the pupil (Lowenstein,

1950). Pupil diameter can range from 1.5 to more than

9 millimeters in humans, and a little time, just about

0.2 seconds, it is required by the muscles of the iris to

react to stimulation (Goldwater, 1972). The ANS in

its role of maintaining homeostasis is in a state of

constant fluctuation (Malpas, 2010), (Hreidarsson

and Gundersen, 1988). This fluctuation, expressed by

spontaneous variations in the rhythmic changes in

pupil-size of around 1% occurs with heart beats and

Villalobos-Castaldi, F., Ruiz-Pinales, J., Kemper-Valverde, N., Flores-Flores, M., Ramírez-Sánchez, L. and Ortiz-Hernández, M.

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform.

DOI: 10.5220/0005697400670077

In Proceedings of the 9th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2016) - Volume 4: BIOSIGNALS, pages 67-77

ISBN: 978-989-758-170-0

breathing due to fluctuations in blood pressure

(Warga, et al, 2009). The variance of normal pupil

size is very large. When a constant light level is

maintained, the pupil is seen to exhibit continual

fluctuations called Spontaneous pupillary

fluctuations (SPF) or pupil unrest or physiological

hippus. These variations in pupil size is a

characteristic of the regulatory mechanism and it is

often said that it shows a state of pupillary unrest.

This is a physiologic phenomenon that represents a

dynamic equilibrium of pupil size of the sympathetic

and para-sympathetic activity modulated by the

central nervous system is responsible (Newman,

2008), (Nowak et al., 2008). A typical recording of

pupil size in a constant light source shows marked

spontaneous activity with an irregular pattern of a

periodic oscillation. Unrest amplitudes are highest for

medium pupil sizes (Rosenberg and Kroll, 1999).

2 RELATED WORKS

In the nighties (McLaren et al., 1992) the authors

developed digital filtering techniques and Fourier

analysis to calculate several parameters designed to

report hippus and miosis. These techniques provided

a quantitative manner to evaluate pupillograms to be

used in the assessment of alertness. The first

parameter designed to report hippus was derived from

the Fourier-transformed pupillogram and was the area

of the frequency spectrum in a selected band of

frequencies. A second parameter to report hippus was

also investigated. Spectra differ the most at low

frequencies. At higher frequencies, differences were

seen to diminish.

A fast Fourier transformation was carried out as a

vigilance objective test for frequencies from 0.0 to 0.8

Hz in (Lüdtke et al., 1998) with the purpose of

detecting fatigued waves, i.e., slow pupillary

oscillations. For temporal changes analysis in the

frequency domain of pupillary oscillation two

parameters were extracted. One parameter based on

the FFT regarded only frequencies below 0.8 Hz,

neglecting fast pupillary changes (>1.5625 Hz). An

additional parameter referring to the tendency for

pupil instability, the pupillary unrest index (PUI), was

defined by cumulative changes in pupil size based on

mean values of consecutive data sequences. The

power and PUI were compared using the Mann–

Whitney U-test. Both parameters showed significant

differences between the two groups. The main

differences between an alert and a sleepy group of

people in power and PUI demonstrated the usefulness

of this method to objectively detect and quantify

sleepiness.

The study purpose reported in (Calcagnini et al,

2000

) was to assess whether and the extent LF and

HF rhythms contribute to spontaneous pupil diameter

fluctuations in rest and during sympathetic activation.

To investigate the statistical properties of the SPDF,

a parametric spectral and cross-spectral estimation

was used. The spectral coherences were used to

quantify the statistical link among rhythms in

different signals. A rhythmic respiratory component

(HF) was clearly found at 0.25 Hz in the pupillogram

spectrum in all the subjects. Cross spectral analysis

showed a significant coherence in this band between

pupil and respiration, pupil and tachogram, and pupil

and systogram (Cerutti, 2000).

In conclusion the analysis of the SPF showed the

contribution of two specific harmonic components,

which have been found to correspond to the well-

known LF and HF rhythms of the Heart Rate and

Blood Pressure variability signals (Cerutti, 1997).

Additionally, the authors concluded that the

apparently stochastic behavior of the spontaneous

PDF hides specific harmonic components reflecting

autonomic activity (Cerutti, 1999).

In the two thousands (Nowak et al, 2008) the

authors developed a new method of variability

description for the Spontaneous Pupillary Fluctuation

(SPF) signals based on the time-frequency analysis by

studying the variability of the SPF signal spectrum.

The application of fast pupillometry for recording the

SPF permitted expanding the analyzed frequency

band to 20 Hz. The proposed method of analysis and

the introduced measures of SPF variability helped

them in the detection and quantitative description of

short-lasting time-frequency and time-amplitude

variations that were obscured by the overall spectral

analysis (Elsenbruch, 2000). The authors mentioned

that the Fourier Transform (which requires a

stationary signal and is commonly used in the spectral

analysis of SPF), has limitations in signal testing. It

was concluded that the SPF signal is non-stationary,

i.e. its spectrum is varying in time. Thus, it was

clearly demonstrated that the previous assumptions

are no longer valid (Longtin, 1989).

The previous belief was that fluctuations in pupil

diameter arose from random processes, but new

results from chaotic time series has shown that they

may also arise from deterministic systems

(Rosenberg and Kroll, 1999). The accumulated

evidence supports the notion that the dynamics of

pupil size are governed by deterministic chaos rather

than a linear or stochastic process, and this has been

demonstrated by analyzing the pupil size versus time

from six subjects using pupillography and nonlinear

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

techniques (Rosenberg and Kroll, 1999). The

examined values of the correlation dimension, the

Hurst exponent, the flat power spectra, the values of

the Lyapunov exponent, and phase plane analyses

indicate a chaotic system as the origin of the

phenomenon. Pupil activity reported showed

repetitive complex patterns which could be explained

by a chaos rather than a random system (Rosenberg

and Kroll, 1999).

As previously mentioned, the SPF signal analysis

has been used for monitoring the level of alertness in

clinical conditions, diagnosing sleep disorders,

assessing how the different rhythms of the SPS

contribute to spontaneous pupil diameter fluctuations

at rest and during sympathetic activation, and also for

assessing the efficacy of therapeutic interventions

(Boyina et al., 2012), (Naber et al., 2013), (Jain et al.,

2011), (Heaver, 2012), (Calcagnini et al., 2000

(Bouma and Baghuis, 1971), (Pedrotti et al., 2014),

(Regen et al., 2013) and (Lüdtke et al., 1998). These

analyses have generally been performed by spectral

indices computed from standard spectral analysis

techniques (as the Fast Fourier Transform). Such

methods have generated comparable results but

cannot account for the unavoidable inter-individual

variability that naturally occurs in the pupillary

fluctuation signals. There are some crucial

restrictions using these techniques: the system must

be linear and the data must be strictly stationary;

otherwise, the features extracted via the Fourier

Transform do not have any physiological significance

(Boyina et al., 2012), (Cong, Z. 2009).

Ephemeral nature of many physiological events

indicates associated data are non-linear and non-

stationary waves. Even so, data being non-stationary

has not received the proper attention and its effects

are frequently disregarded. Serious consequences of

such assumptions are inaccurate results or incorrect

interpretation of the underlying physics.

Even if under exceptionally general conditions,

Fourier transform may be used by those methods, it

exists some basic limitations: indeed the system has

to be linear and the data must be strictly periodic or

stationary. Hence, if conditions are not keep within

such limits, then the resulting spectrum will not make

any sense physically at all, and Fourier spectral

analysis based methods will be considered of limited

use. Having no alternatives, current works are still

using Fourier spectral analysis to process such data

(Huang, N., 2005). (Faust and Bairy, 2012). At the

end, methods which do not assume a stationary status

(Cong , Z., 2009) are hardly desirable to have.

In the light of such conditions, it is clear that

computer methods using Fourier spectral analysis are

of limited use. Shortly, both the indiscriminate use of

Fourier spectral analysis and the acceptance of the

stationary and linearity sates may give wrong results,

some of them are described below. (Huang, N., 2005).

(Faust and Bairy, 2012). It is desirable to employ

quantitative methods which do not assume a

stationary status (Cong, Z., 2009). The Hilbert Huang

Transform (HHT) initially developed for natural and

engineering sciences and now is applied to financial

data (Huang et al., 2003). The HHT method is

specially developed for analyzing non-linear and non-

stationary data.

Nowadays, several methods are available for the

time-frequency analysis of non-stationary signals.

For instance, the short-time Fourier transformation

(STFT) can be used when the signal is piece-wise

stationary, whereas the wavelet transform can be used

for linear non-stationary signals (Wu and Huang,

(2005). One drawback of the wavelet transform is that

a priori knowledge about the signal to analyze is

needed in order to choose a suitable wavelet. Another

drawback is that its time-frequency resolution is

limited by the Heisenberg-Gabor uncertainty

principle. In contrast, the HHT can be used to analyze

non-linear and non-stationary signals with excellent

resolution in both time and frequency (Barnhart and

Eichinger 2011) and (Barnhart, 2011).

3 HILBERT HUANG

TRANSFORM

HHT’s development was motivated by the need to

describe non-linear and non-stationary distorted

waves in detail (Huang and Long, 2006). It was

designated by the National Aeronautics and Space

Administration (NASA) Goddard Space Flight

Center (GSFC), and pioneered by (Huang, Long and

Shen, 1996), (Huang et al., 1999), (Huang et al.,

1998), (Huang et al., 2003), (Huang and Shen, 2005)

and (Huang et al., 2007). Since this new analysis

technique was developed, it has shown the ability to

analyze non-linear and non-stationary data in many

areas of research (bio-signal, chemistry, chemical

engineering, financial applications and others).

Different from many of the previous transform

methods, like Fourier-based techniques [wavelet and

fast Fourier Transform], this remarkable method is

intuitive, direct, a posteriori, and adaptive; and

consequently, highly efficient. Mainly because its

origin rise from the decomposition based on and

derived from the physical signal. The bases so derived

have no close analytic expressions, and they can only

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform

be numerically approximated. (Huang, N. 2005).

This decomposition method is adaptive, and

therefore, highly efficient. As indicated by (Flandrin

et al., 2004), one of the advantages of the HHT is that

its data driven criteria is not fully dependent on

theoretical input or formula. Also, the HHT analyzes

non-stationary signals locally.

There are two processes involved in the HHT: the

Empirical Mode Decomposition (EMD) and the

Hilbert Spectral Analysis (HSA). The key part of the

method is the pre-processing step, the EMD, in which

any complicated data set can be decomposed into a

finite and often small number of Intrinsic Mode

Functions (IMF). With the Hilbert transform, the IMF

yields instantaneous frequencies as functions of time

that give sharp identifications of imbedded structures

(Huang et al., 2003). The final presentation of the

results is a time-frequency-energy distribution, which

was designated as the Hilbert Spectrum. Comparisons

with the Wavelet and Fourier analyses showing that

the HHT method offers much better temporal and

frequency resolutions.

The Hilbert transform, , of any function or

signal  is given by:













≡























(1)

where PV denotes the Cauchy’s principle value

integral.

An analytic representation of the signal can be

formed with the Hilbert transform pair as:

































(2)

where



















/

(3)



















,

and



√

1









and 







are the instantaneous amplitudes and

phase functions, respectively (Huang et al., 2001).

The instantaneous frequency can be computed by

means of:







(4)

In order to apply the Hilbert transform to a signal, it

must first be converted to a symmetric signal with

mean zero and no negative maxima and no positive

minima. The Empirical Mode Decomposition (EMD)

is a method to reduce a signal into a collection of

intrinsic mode functions with “well-behaved” Hilbert

transforms. Unlike the Fourier series or transform,

this representation allows a simultaneous

understanding of the signal in both frequency and

time.

3.1 Empirical Mode Decomposition

Empirical Mode Decomposition (EMD) is a tool

which provides a signal-adaptive decomposition

useful for the analysis of non-stationary and non-

linear data and shows a strong capability to precisely

adjust to the spectral content of the analyzed data. It

is based on the concept that any complicated set of

data can be decomposed into a finite and often small

number of mono-component signals called the

Intrinsic Mode Functions (IMF) which are associated

with different spectral contributions and then

applicable to compute the physical meaning of the

complex signal. Decomposition of a signal is made

through an iterative process to cancel out the local

means from the signal. The sifting process is as

follows:

1. Compute all the local extrema (maxima and

minima).

2. Obtain the upper envelope by connecting all the

local maxima with a cubic spline.

3. Repeat for all the minima to obtain the lower

envelope.

Then, the mean of the splines is subtracted from the

original signal. The sifting process is repeated with

the resulting residual signal until the mean and

standard deviation of the average spline is near zero.

The resulting residual signal meets the definition of

an IMF. An IMF is therefore defined as a signal with

zero-mean, and number of extrema and zero-

crossings differing by at most one (Huang et al.,

1998), (Huang et al., 1999) and (Huang et al., 2003).

This first IMF is subtracted from the original signal

and the whole sifting process is repeated with this

new residual signal. The decomposition process stops

when the residue is a monotonic function which not

an IMF. The last extracted IMF corresponds to the

trend which is the lowest frequency component of the

signal.

As a result, the original signal  can be written in

terms of the IMFs and the final residue as:





























(5)

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

Using equations 2 and 3, the analytic function can be

written as:

















































(6)

This function has a similar form to the Fourier

decomposition of a signal



































(7)

Thus, the EMD decomposition can be regarded as a

generalized Fourier decomposition. Unlike the

Fourier transform, which is predicated on a priori

selection of basic functions that are either of infinite

length or have fixed finite widths, this empirical

decomposition method is adaptive, and, therefore,

highly efficient (Cong, Z., 2009). Since the

decomposition is based on the local characteristic

data time scale, it is applicable to non-linear and non-

stationary processes. The EMD is also useful as a

filter to extract variability of different scales. At a

signal time instance, only a single frequency

component exists. The EMD method is a necessary

data pre-processing before the Hilbert transform can

be applied (Huang, N.E., 2003).

4 DATA PROCESSING AND

ANALYSIS

A data set of 44 documented pupillary records of

healthy university students has been analyzed. Length

of signals are one minute at a rate of 30 fps. Details

of the collected data are: an IR video camera was used

for recording one eye only, typically the left eye, and

they were done under constant luminance level (40

cd/m

). Frame by frame, pupil images were recorded

and transferred by means of a video capture board

providing real-time digitizing besides the video

sequences. The video-capture board was ﬁtted by

USB on a Pentium® Dual-Core T4200 @ 2 GHz and

4 GB of internal memory; MATLAB 7.10 (R2013a)

was used to obtain real time recordings of the movie.

The video sequences were collected from subjects in

a resting condition, that is, they were seated on a

comfortable chair. Experiment facilities were located

in a quiet usability laboratory. For readers going into

details about the infrared video Pupillography system

and the image processing method, please refer to

(Villalobos and Suaste, 2013).

Following the procedure described above (EMD

algorithm) the SPO signals were decomposed into

their IMF components. To exemplify the results

obtained from EMD, in Figure 1 a segment of the IMF

components obtained from a selected SPO signal

(black line) are shown. In this example, the algorithm

yielded 8 components (blue lines) plus a residue R

(red line). Each IMF has a distinctive amplitude and

frequency content. For the whole data set (44

pupillograms), the number of IMFs needed to

decompose the signals fluctuates from 4 to 10 modes

(plus the non-linear trend or residue R) Huang et al.,

indicated that the broad number of modes extracted

from a signal is approximately equal to log

(N),

where N is the number of points per signal (Huang et

al., 2003). The values obtained in this study fall

within the limits set by that expression.

The intra signals variations could be due to the

informative nature of the IMFs, and is evidence of the

numerous and different factors that direct each

subject’s response. A remarkable advantage of the

decomposition is that the local variation of the pupil

area can be observed directly, the intrinsic

oscillations emerge naturally and, based on

knowledge of the monitored phenomena, solid

conclusions can be obtained about the meaning of

each mode and its relationship to particular behaviors.

Even the residue has a sounded meaning; it keeps

the mean pupil diameter without fast and short lasting

pupil oscillations. The non-linear trend, hallmark of a

non-stationary process, is negative because it slowly

decays through the time scale (Papoulis and

Saunders, 1989). Concerning the frequency and

energy levels involved in the residual component,

from now on, in the IMFs analysis they will be

excluded.

Once the signals were decomposed into their

IMFs, a numerical proof of completeness is

necessary. The numerical reconstruction of the

selected example is as follow:

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform

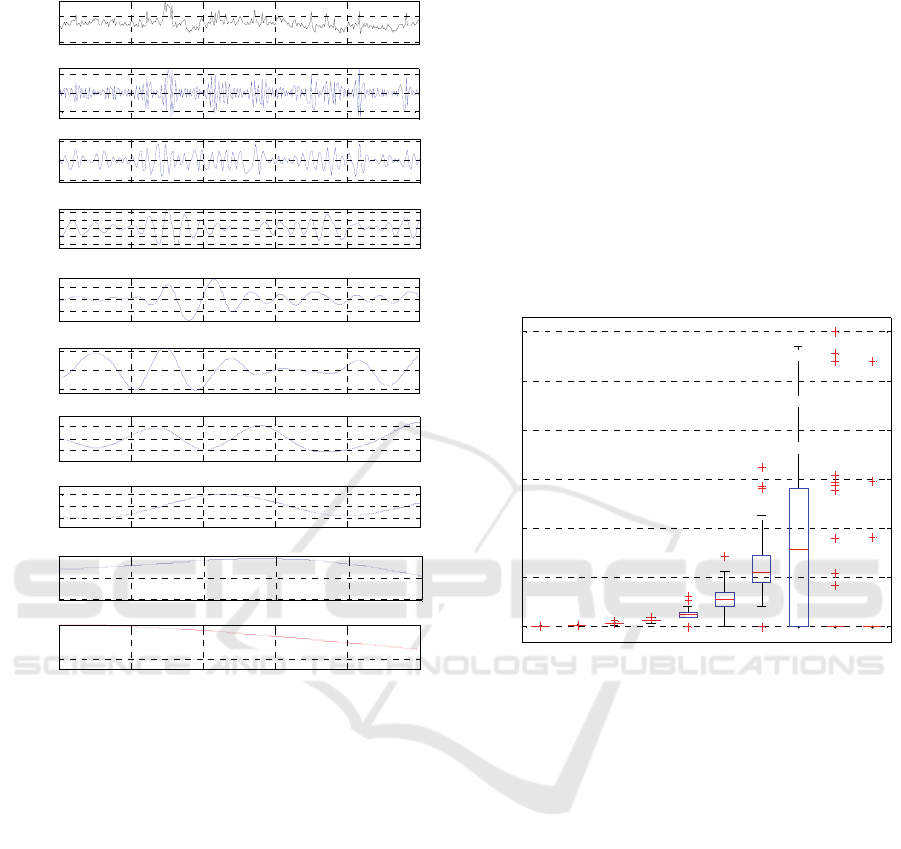
Figure 1: EMD processing of a typical SPF signal. The top

panes is the original signal, imf1 to imf8 are the modes and

res is the residue.

Adding R to each component, starting from the

longest period component to the shortest (IMF1), the

original signal is recreated. When the procedure has

reached the IMF2 the original series has been

practically recovered (total energy contained in the

original SPO data). The latest component (IMF1)

does not contribute significantly to reassemble the

signal, actually it can be seen as noise. The

completeness was numerically verified for the whole

data set. The IMFs pertinence was proved through

null differences between the original signals and the

sum of the components.

4.1 IMF Statistics

In order to clarify the meaning of the IMFs and to use

them adequately to describe the studied phenomena,

the modes are characterized by well-known statistics

metrics.

4.1.1 Period

Based on the definition of the IMF function which

established that the frequency of an IMF can change

continuously with time, the signal period is assumed

as not constant (Huang et al., 2003). The IMF period

can be calculated by dividing the number of data

points by the number of peaks (local maxima). So, if

T is the length of the IMF component and s the

number of peaks, then, the IMF period is equal to T/s.

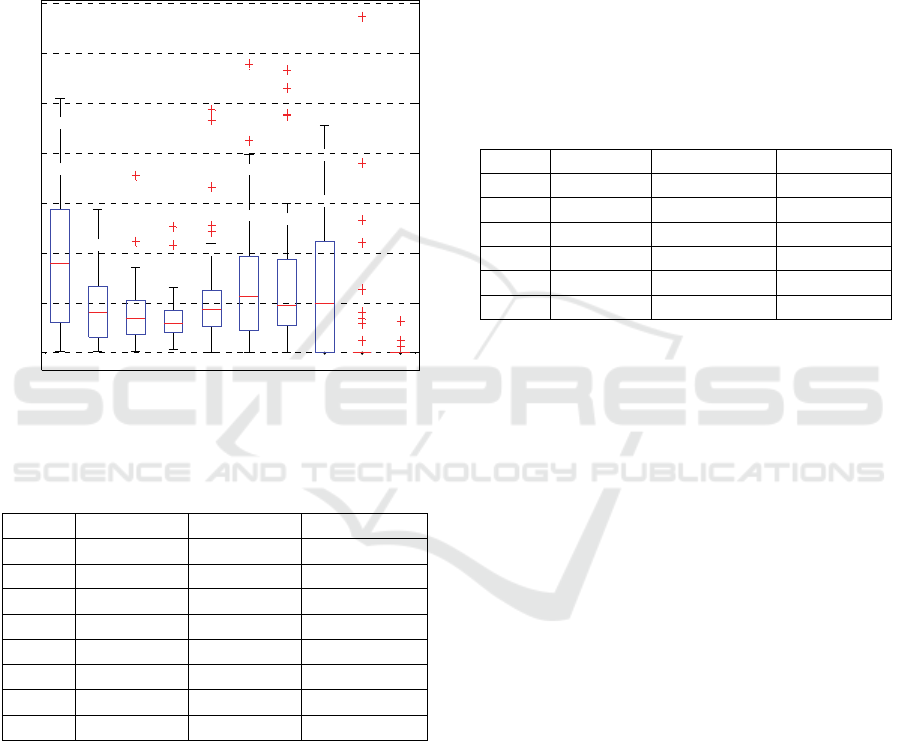
A boxplot for the mean period versus IMFs is

depicted in Figure 2.

Figure 2: Boxplot for the period content according to the

IMF index.

The first mode has the smallest mean period (~3), and

for the successive components the mean period

doubling is followed. For the last mode, the period

variability is evident going from values near zero to

the maximum that almost reaches 600 which is

indicative of very slow pupillary oscillations. About

the period doubling, it is more evident in the first

modes and not clearly verified for the last 2 modes;

this may be due to the increasingly noticeable

presence of noisy components as the decomposition

process approaches the residue.

As observed in the graph, there are not significant

period differences in the whole data set when

analyzing each mode separately. It is important to

note that the period significantly changes in the 8

IMF.

4.1.2 Variance

The mean variance contribution from each IMF was

0 2 4 6 8 10

O riginal

signal

Empirical Mode Decomposition

time [seconds]

0 2 4 6 8 10

-0.5

0.5

imf1

time [seconds]

0 2 4 6 8 10

-0.5

0.5

imf2

time [seconds]

0 2 4 6 8 10

-0.4

-0.2

0.2

0.4

imf3

time [seconds]

0 2 4 6 8 10

-0.2

0.2

imf4

time [seconds]

0 2 4 6 8 10

-0.2

0.2

imf5

time [seconds]

0 2 4 6 8 10

-0.1

0.1

imf6

time [seconds]

0 2 4 6 8 10

-0.1

0.1

im f7

time [seconds]

0 2 4 6 8 10

-0.2

0.2

imf8

time [seconds]

0 2 4 6 8 10

7.5

res.

time [seconds]

200

400

600

800

1000

1200

12345678910

IMF

Period

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

also computed. The variance is used as a simple and

intuitively benchmark to determine the significance

of each component (IMF) of the original signal. Thus,

components with larger variance are more significant.

It was found that the contribution of each IMF to

the total variance also changes from signal to signal

Figure 3 illustrates the boxplot for the variance

contribution (%) depending on the IMF component

number.

Figure 3: Boxplot for the variance content according to the

IMF index.

Table 1: Variance content for a selected subject.

IMF VAR VAR (%) ∑ (%)

1 0.0479 31.7013 31.7013

2 0.0305 20.1545 51.8559

3 0.0219 14.4560 66.3119

4 0.0124 8.2111 74.5230

5 0.0089 5.9113 80.4344

6 0.0068 4.4731 84.9074

7 0.0061 4.0455 88.9529

8 0.0167 11.0471 100.0000

Table 1 gives the contribution of each IMF to the total

sum of variances for a selected subject in absolute

terms, % of total variance and cumulative % variance

contribution.

In this table it is possible to see the large

differences in the variance contribution from each

IMF to the total variance within the selected signals.

Based on the variance content reported in Table 1, it

is concluded for this specific subject, that the most

important components are the highest frequency

modes (IMF1, 2 and 3); the sum of variances for these

important components contribute 66.31% of the total

variance, but the low frequency components have less

effect on the whole change of this SPO signal. The

variance intervals of the first components are wide

and grow as the mode index increases.

Conversely to the last case, in the SPO wave

presented in Table 2, the most important IMF

components are the lowest frequency modes (IMF4,

5 and 6), and their variance sum contributes

86.5874% of the total variance. Therefore, the high

frequency components have less effect on the total

variance of the signal. The interval of the higher

frequency components is narrow while the interval of

the lower frequency modes becomes wider.

Table 2: Variance content of another selected subject.

IMF VAR VAR (%) ∑ (%)

1 0.0007 3.7769 3.7769

2 0.0004 1.9960 5.7729

3 0.0014 7.6397 13.4126

4 0.0038 21.4697 34.8822

5 0.0083 46.6456 81.5279

6 0.0033 18.4721 100.000

As can be concluded, the frequency at which the

highest variance contribution occurs changes from

signal to signal, so the highest variance content for

each signal is present on different IMFs.

4.2 Instant Amplitude and Frequency

Analysis

Having obtained the IMF components, it is not

difficult to apply the Hilbert transform to each IMF

component in order to compute the instantaneous

amplitude and frequency according to equation 3 and

4. The combination of the EMD and the Hilbert

Spectral Analysis is designated as the Hilbert–Huang

Transform (HHT).

4.2.1 Instant Amplitude

Figure 4 shows the boxplot of the amplitude

contribution according to the number of IMFs. As can

be seen, there is a large variation between

components and they are highly intermittent through

the time span. The amplitude variation between

modes leads to the conclusion that for the studied

phenomenon and analyzed population a particular

IMF cannot be selected as the one that contains the

higher energy levels. The mean amplitude

contribution of all components is in the 0.1-0.2 mm

interval.

The amplitude has a slight tendency to decrease as

12345678910

IMF

Variance (%)

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform

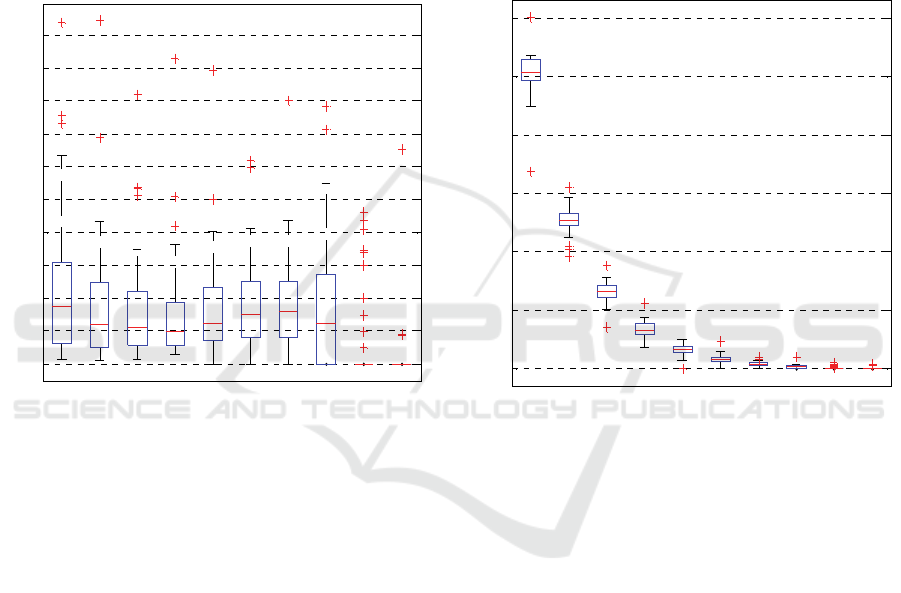
the number of IMFs increases. However, in the first

and last modes (8

IMF, which is the most

representative before reaching R) the fluctuations of

the pupil area are wider (~0 - 0.3mm). The amplitude

intervals of in-between modes become high and are

mainly concentrated below the ~0.25 mm range. It is

evident that there is a wide inter-subject variation and

no major modes are detected, i.e. the highest

amplitude values for each signal (subject) are on

different IMFs. While for some subjects the

amplitude is higher at the first modes, for others the

maximum values are present at superior.

Figure 4: Boxplot for the amplitude content according to the

IMF index.

There are interesting responses to be noted:

a) Where amplitude levels are almost equally

distributed in all modes,

b) Where amplitude values different from zero are

only present in the first modes, 1

to 4

IMFs and,

c) Where the amplitude concentration cannot be

referred to trends a) nor b).

4.2.2 Frequency

Figure 5 illustrates the boxplot of the frequency

variation according to number of IMFs. As can be

observed, the frequency value progressively falls as

the mode number increases. The frequency range of

each IMF is well defined and independent of others.

There are marked differences between the limits of

the frequency characteristic of each mode. It is

verified that the highest frequencies are contained in

the first components and, consequently, the latest

modes have the lower frequency levels. The variation

intervals become narrower as the IMF index is higher.

The first mode has the highest frequency content

(~ 9 Hz to ~11 Hz), the 2

IMF frequency is around

5 Hz while from the 3

to 8

modes the activated

frequencies go from ~3 Hz to ~ 0.01 Hz. Observing

the response trends defined concerning amplitude

behavior, interesting relationships can be

pronounced.

There are subjects with strong pupillary

oscillations at the first modes; at the highest

frequency levels, others present them at the higher

modes and at the lower frequency levels.

Figure 5: Boxplot for the frequency content according to the

IMF index.

With regard to the highlighted responses:

a) Some subjects respond with similar amplitude

levels at every frequency detected,

b) The behavior of the subjects having zero

amplitudes in the higher modes must be

interpreted as responses only in the highest

frequency levels and,

c) Some individuals have reactions that activate

frequencies below 1 Hz.

The differences in the frequency content and their

association with the amplitude has an clear effect on

the conclusions about the studied phenomenon, the

stationary statement (signals) and even on the

classification system that generates the data as

nonlinear.

4.3 Spectral Analysis

Having obtained the IMF components, the next step

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

12345678910

IMF

Am plitude (mm )

12345678910

IMF

Frequency (Hz)

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

in the proposed method is to apply the Hilbert

Transform to each component and generate the

Hilbert Spectrum (HS). Having the Hilbert Spectrum

defined, we can compute the Marginal Spectrum

(MS) that offers a measure of total amplitude (or

energy) contribution from each frequency value. In

other words, the MS represents the cumulated

amplitude over the entire data spam. So the MS is the

HS that was integrated through all time. In this

simplification, the time coordination is lost as in the

Fourier spectral analysis, which leave a summary of

the frequency content of the event.

The frequency in either HS or MS has a

completely different meaning from results generated

by applying Fourier spectral analysis. The existence

of energy at a particular frequency in the Fourier

representation, means a component of a sine or a

cosine wave persisted through the time span of the

data. So the existence of energy at the particular

frequency, means only that, in the whole time span of

the data, that there is a higher like hood for such a

wave to have appeared locally.

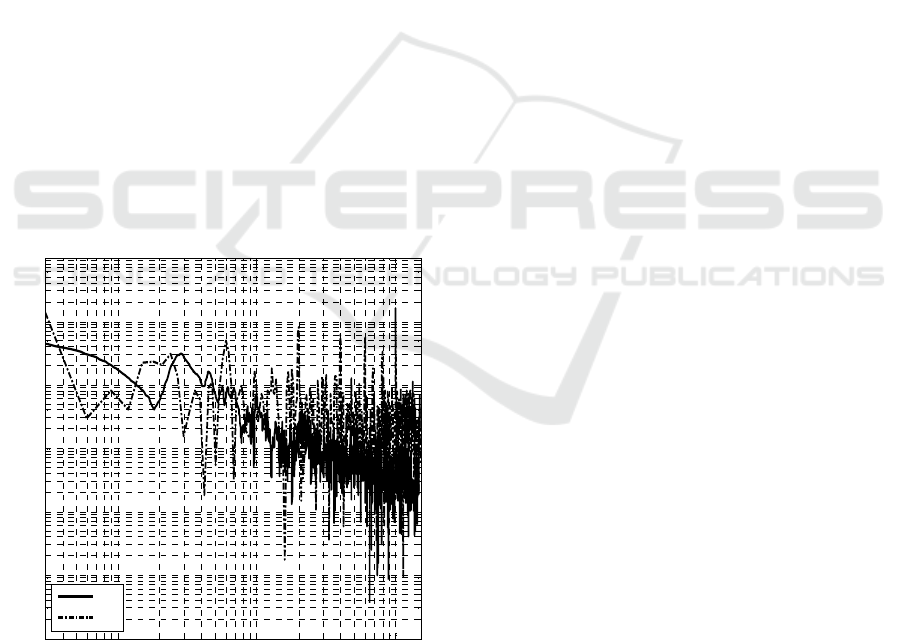
In order to try to compare the proposed spectral

representation method against Fourier conventional

method, we performed a standard FT analysis. In

Figure 6 we directly compare the obtained MS (solid

line) against the conventional Fourier technique

(dotted line) of the SPO data from the Figure 1.

Figure 6: Power spectra of SPF data.

It can be seen that the Marginal spectrum differs from

the Fourier based spectrum in two main issues.

Although the spectral density at the low-frequency

portion is higher in the Hilbert spectra, the Fourier

spectrum is dominated by the DC term due to the non-

zero mean pupil area, this is also meaningless because

of the non-stationary of the data. The spectral density

is lower than the Fourier analysis at higher

frequencies, which was expected because of the

different interpretation of the HHT’s and the Fourier-

based method of data non-linearity. Most of the

Fourier-based techniques always decompose a

nonlinear signal into its base frequency and higher

harmonics; because of this some spectral energy in

the higher frequencies is leaked from their lower

frequency sub harmonics. The HHT interprets signal

non-linearity in terms of frequency modulation, and

the spectral energy of a nonlinear signal remains at

the neighborhood of the base frequency (see Figure

6).

These findings coincided with the ones reported

by (Nowak et al.2008), where by the application of

fast pupillometry for recording and extended spectral

analysis in examining SPO signals, they found

interesting frequency components in some subjects in

the range above 1 Hz. They also reported the

existence of several harmonics even up to 20 Hz

frequency range. The analysis they carried out

showed that the distribution of the PSD amplitude

peaks was different for different frequencies.

Contrary to their proposed method where they

considered the computed numerical parameters as

global, we represent the pupil area fluctuation tacking

advantage of the instantaneous frequency approach,

which even under the worst conditions, is still

consistent with the physics of the system being

studied and could represent it much more accurately

than previous techniques based on Fourier analysis.

5 CONCLUSIONS

This paper has addressed to the possibility of

characterizing the natural behavior of Spontaneous

Pupillary Oscillation SPO records by the time-

frequency signal variations. The objective of

describing data from non-traditional perspectives

(time-frequency-intensity domain) and for finding

specific and indicative behavior patterns is addressed

by applying the HHT to the SPO waves. Non-linear

and non-stationary intrinsic characteristics of these

signals are discovered and reported in this paper using

the advantageous non-traditional signal processing

technique.

The EMD was implemented to decompose the

original SPO signals; the obtained IMF modes

varying from 4-10 plus a non-linear trend which also

-1

-9

-8

-7

-6

-5

-4

-3

Frequency (Hz)

Spectral density

Marginal vs Fourier analysis

HHT

FFT

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform

showed a clear non-stationary behavior. The fact that

the EMD analysis decomposed the spatially

distributed SPO data into a set of natural oscillations

(Khademul, 2006), showed the IMFs are more

effective in isolating physical processes of various

time scales and are also statistically significant.

The obtained results, lead us to observe that the

SPO signals present local and intermittent pupil area

variations in time. The EMD successively extracts the

IMFs starting with the highest local spatial

frequencies in a recursively way, which is effectively

a set of successive low-pass spatial filters based

entirely on the properties exhibited by the data

(Khademul, 2006). It is also observed that there are

wide inter-subject differences in the variance, period,

amplitude, and frequency contribution from each

mode to the total signal. These inter-mode variations,

lead us to the conclusion that for the studied

phenomenon and analyzed population, a particular

IMF cannot be selected as the one that contains the

higher amplitude level or dominant frequencies.

Our characterized analysis is of a preliminary

nature and many issues have to be addressed and

investigated rigorously, and from the obtained results,

the HHT seems to have much more potential for this

initial approach. Applying non-traditional

alternatives to the study of the pupillograms presents

a great opportunity to understand behaviors and to

mitigate diseases or specific medical conditions, for

example: discern between well and diseased states,

explore if SPF records could provide information for

the evaluation of the psychophysiological response of

ANS to affective triggering events or as a quantitative

way in the assessment of alertness.

As the SPO signals are not stationary, the Fourier

spectrum is meaningless physically, in contrast, we

have demonstrated that with the HHT as analytic

method, the resulting frequency-energy spectrum

provides a physical meaningful interpretation of the

signal.

REFERENCES

Barnhart, B. and Eichinger, W., (2011). Empirical Mode

Decomposition applied to solar irradiance, global

temperature, sunspot number, and CO2 concentration

data. Journal of Atmospheric and Solar-Terrestrial

Physics, 73(13), pp.1771-1779.

Barnhart, B.L., (2011). The Hilbert-Huang Transform:

theory, applications, development, PhD thesis,

University of Iowa.

Bouma, H., and Baghuis, L., (1971). Hippus of the pupil:

Periods of slow oscillations of unknown origin. Vision

Research, 11(11), 1345-1351.

Boyina,S.R, Anu.H, Moneca.K, Mahalakshmi Malini.G,

Priyadharshini.R, (2012). Pupil Recognition Using

Wavelet And Fuzzy Linear Discriminant Analysis For

Authentication, International Journal Of Advanced

Engineering Technology, IJAET/Vol.III/ Issue II.

Calcagnini, G., Censi, F., Lino, S., and Cerutti, S., (2000).

Spontaneous fluctuations of human pupil reflect central

autonomic rhythms. Methods Inf Med, 39(2), 142-145.

Cerutti, S., (1997). Cardiovascular autonomic rhythms in

spontaneous pupil fluctuations, Computers in

Cardiology 1997 CIC-97.

Cerutti, S., (1999). Baroceptor-sensitive fluctuations of

human pupil diameter", Computers in Cardiology,Vol

26 (Cat No 99CH37004) CIC-99.

Cerutti, S., (2000). Pupil diameter variability in humans,

Proceedings of the 22nd Annual

InternationalConference of the IEEE Engineering in

Medicine and Biology Society (Cat No 00CH37143)

IEMBS-00.

Cong, Z., (2009). Hilbert-Huang transform based

physiological signals analysis for emotion recognition,

2009 IEEE International Symposium on Signal

Processing and Information Technology (ISSPIT), 12.

De Souza Neto, E., Abry, P., Loiseau, P., Cejka, J., Custaud,

M., Frutoso, J., Gharib, C. and Flandrin, P. (2007).

Empirical mode decomposition to assess cardiovascular

autonomic control in rats. Fundam Clin Pharmacol,

21(5), pp.481-496.

Elsenbruch, S., (2000). Physiological Measurement, 05.

Faust, O. and Bairy, M., (2012). Nonlinear analysis of

physiological signals: a review. J. Mech. Med. Biol.,

12(04), p.1240015.

Flandrin, P., Rilling, G., and Goncalves, P., (2004).

Empirical mode decomposition as a filter bank. Signal

Processing Letters, IEEE, 11(2), 112-114.

Goldwater, B., (1972). Psychological significance of

pupillary movements. Psychological Bulletin, 77(5),

pp.340-355.

Heaver, B., (2012). Psychophysiological indices of

recognition memory (Doctoral dissertation, University

of Sussex).

Hreidarsson, A. B., and Gundersen, H. J. G.,

(1988).Reduced Pupillary Unrest: Autonomic Nervous

System Abnormality in Diabetes Mellitus, Diabetes.

Huang, N. (2005). Empirical mode decomposition for

analyzing acoustical signals. The Journal of the

Acoustical Society Of America, 118(2), 593.

http://dx.doi.org/10.1121/1.2040268.

Huang, N. E., and Shen, S. S., (2005). Hilbert-Huang

transform and its applications (Vol. 5). World

Scientific.

Huang, N. E., Long, S. R., and Shen, Z., (1996). The

mechanism for frequency downshift in nonlinear wave

evolution. Advances in applied mechanics, 32, 59-

117C.

Huang, N. E., Shen, Z., and Long, S. R., (1999). A new view

of nonlinear water waves: The Hilbert Spectrum 1.

Annual review of fluid mechanics, 31(1), 417-457.

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H.

H., Zheng, Q. and Liu, H. H.,(1998). The

BIOSIGNALS 2016 - 9th International Conference on Bio-inspired Systems and Signal Processing

empirical mode decomposition and the Hilbert

spectrum for nonlinear and non-stationary time series

analysis. Proceedings of the Royal Society of London

Mathematical, Physical and Engineering Sciences (Vol.

454, No. 1971, pp. 903-995). The Royal Society.

Huang, N., Wu, M., Qu, W., Long, S., and Shen, S., (2003).

Applications of Hilbert-Huang transform to non-

stationary financial time series analysis. Appl.

Stochastic Models Bus. Ind., 19(3), 245-268.

Huang, N.E., and Long, S., (2006). On the Normalized

Hilbert Transform and Its Applications in Remote

Sensing, Signal and Image Processing for Remote

Sensing.

Huang, N.E., (2003). Applications of Hilbert-Huang

transform to non-stationary financial time series

analysis, Applied Stochastic Models in Business and

Industry, 7.

Huang, Y., Schmitt, F. G., Lu, Z., and Liu, Y.,(2007).

Empirical mode decomposition analysis of

experimental homogeneous turbulence time series. In

21° Colloque GRETSI, Troyes, FRA, 11-14 septembre

2007. GRETSI, Groupe d’Etudes du Traitement du

Signal et des Images.

Jain, S., Siegle, G., Gu, C., Moore, C., Ivanco, L.,

Studenski, S., Greenamyre, J. and Steinhauer, S.,

(2011).Pupillary unrest correlates with arousal

symptoms and motor signs in Parkinson disease.

Movement Disorders, 26(7), pp.1344-1347.

Khademul, I.M., (2006)."Empirical mode decomposition

analysis of climate changes with special reference to

rainfall data", Discrete Dynamics in Nature and

Society.

Longtin, A., (1989). Nonlinear Oscillations, Noise and

Chaos in Neural Delayed Feedback department of

Piysics, McGill University, Montréal, Canada.

Lowenstein, O., (1950). Role of Sympathetic and

Parasympathetic Systems in Reflex Dilatation of the

Pupil. Archives of Neurology and Psychiatry, 64(3),

313.

Lüdtke, H., Wilhelm, B., Adler, M., Schaeffel, F., and

Wilhelm, H., (1998). Mathematical procedures in data

recording and processing of pupillary fatigue waves.

Vision Research, 38(19), 2889-2896.

Malpas, S., (2010). Sympathetic Nervous System

Overactivity and Its Role in the Development of

Cardiovascular Disease. Physiological Reviews, 90(2),

pp.513-557.

McLaren, J. W., Erie, J. C., and Brubaker, R. F., (1992).

Computerized analysis of pupillograms in studies of

alertness. Invest. Ophthalmol. Vis. Sci, 33(3), 671-676.

Naber, M., Alvarez, G., and Nakayama, K., (2013).

Tracking the allocation of attention using human

pupillary oscillations. Frontiers in Psychology, 4.

Newman, S., (2008). Clinical Neuro-Ophthalmology. A

Practical Guide. Journal of Neuro-Ophthalmology,

28(4), p.362.

Nowak, W., Hachol, A. and Kasprzak, H., (2008). Time-

frequency analysis of spontaneous fluctuation of the

pupil size of the human eye. Optica Applicata,

XXXVIII, No. 2, pp.269-280.

Papoulis, A., and Saunders, H., (1989). Probability,

Random Variables and Stochastic Processes (2nd

Edition). J. Vib. Acoust. 111(1), 123.

Pedrotti, M., Mirzaei, M., Tedesco, A., Chardonnet, J.,

Mérienne, F., Benedetto, S., and Baccino, T.,

(2014).Automatic Stress Classification with Pupil

Diameter Analysis. International Journal of Human-

Computer Interaction, 30(3), 220-236.

Regen, F., Dorn, H., and Danker-Hopfe, H., (2013).

Association between pupillary unrest index and waking

electroencephalogram activity in sleep-deprived

healthy adults. Sleep Medicine, 14(9), 902-912.

Rosenberg, M. L., and Kroll, M. H., (1999). Pupillary

hippus: an unrecognized example of biologic chaos.

Journal of Biological Systems, 7(01), 85-94.

Sylvain, S., and Brisson,J., (2014). "Pupillometry:

Pupillometry", Wiley Interdisciplinary Reviews

Cognitive Science.

Villalobos-Castaldi, F., and Suaste-Gómez, E. (2013). A

new spontaneous pupillary oscillation-based

verification system. Expert Systems with Applications,

40(13), 5352-5362. http://dx.doi.org/10.1016/

j.eswa.2013.03.042.

Warga, M., Lüdtke, H., Wilhelm, H., and Wilhelm, B.,

(2009). How do spontaneous pupillary oscillations in

light relate to light intensity? Vision research, 49(3),

295-300.

Wu, Z. and Huang, N.E., (2005).Statistical Significance

Test of Intrinsic Mode Functions", Interdisciplinary

Mathematical Sciences.

Spontaneous Pupillary Oscillation Signal Analysis Applying Hilbert Huang Transform