InterCriteria Analysis Applied to Various EU Enterprises
Lyubka Doukovska
1
, Vassia Atanassova
2
, George Shahpazov
1
and František Čapkovič
3
1
Institute of Information and Communication Technologies, Bulgarian Academy of Sciences
Acad. G. Bonchev str., bl. 2, 1113 Sofia, Bulgaria
2
Institute of Biophysics and Biomedical Engineering, Bulgarian Academy of Sciences
Acad. G. Bonchev str., bl. 105, 1113 Sofia, Bulgaria
3
Institute of Informatics, Slovak Academy of Sciences
Dubravska cesta 9, 845 07 Bratislava, Slovak Republic
Keywords: InterCriteria decision making, Intuitionistic fuzzy sets, Index matrix, European enterprises, Micro, small,
medium and large enterprises in EU27, Positive consonance.
Abstract: The present research aims to detect certain correlations between four economic indicators, against which
have been evaluated the economic entities of the European Union with 27 Member States, as split into four
categories: micro, small, medium and large enterprises. The mathematical formalism employed for
revealing these dependencies, particularly termed here ‘positive’ and ‘negative consonances’, is a novel
decision support approach, called InterCriteria Analysis, which is based on the theoretical foundations of the
intuitionistic fuzzy sets and the augmented matrix calculus of index matrices. The proposed approach can be
useful in processes of decision making and policy making, and it can be seamlessly integrated and further
extended to other related application areas and problems, where it is reasonable to seek correlations between
a variety of economic and other indicators.
1 INTRODUCTION
In present work, we make the consequent step in a
series of research, aimed at proposing the
application of the novel approach of InterCriteria
Analysis (ICA) to economic data, aimed at the
discovery of correlations between important
economic indicators, based on available economic
data. At this new step, we take as input information
about the economic enterprises in the EU27, the
European Union with 27 Member States, as grouped
in the four types of enterprises with respect to the
scale: micro, small, medium and large enterprises,
(Calogirou, et al., 2010).
The indicators against which these four types of
EU27 enterprises have been evaluated are four,
namely: ‘Number of enterprises’, ‘Number of per-
sons employed’, ‘Turnover’ and ‘Value added at
factor cost’. Potential discovery of correlations (in
this approach termed as positive consonances)
between economic indicators can bring new know-
ledge and improve decision making and policy
making processes.
The ICA approach is specifically designed for
datasets comprising evaluations, or measurements of
multiple objects against multiple criteria. In the initial
formulation of the method, the aim was to detect
correlations between the criteria, in order to eliminate
future evaluations/measurements against some of the
criteria, which exhibit high enough correlations with
others. This might be the desire, when some of the
criteria are for some reason deemed unfavourable, for
instance come at a higher cost than other criteria, are
harder, more expensive and/or more time consuming
to measure or evaluate. Elimination or reduction of
these unfavourable criteria from the future evaluations
or measurements may be desirable from business
point of view in order to reduce cost, time or
complexity of the process.
284
Doukovska L., Atanassova V., Shahpazov G. and Capkovic F.
InterCriteria Analysis Applied to Various EU Enterprises.
DOI: 10.5220/0005888302840291
In Proceedings of the Fifth International Symposium on Business Modeling and Software Design (BMSD 2015), pages 284-291
ISBN: 978-989-758-111-3
Copyright
c
 2015 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

This paper is organized as follows. The basic
mathematical concepts employed in the ICA method
are presented in Section 2. In Section 3, we present
the input data and the results of their processing. We
report of the findings, produced by the algorithm and
formulate our conclusions in the last Section 4.
2 INTERCRITERIA ANALYSIS
METHOD
The building blocks of the presented InterCriteria
Analysis for decision support are the two concepts
of intuitionistic fuzziness and index matrices.
Intuitionistic fuzzy sets defined by Atanassov
(Atanassov, 1983; Atanassov, 1986; Atanassov,
1999; Atanassov, 2012) are one of the most popular
and well investigated extensions of the concept of
fuzzy sets, defined by Zadeh (Zadeh, 1965). Besides
the traditional function of membership µ
A
(x) defined
in fuzzy sets to evaluate the membership of an
element x to the set A with a real number in the
[0; 1]-interval, in intuitionistic fuzzy sets (IFSs) a
second function has been introduced, ν
A
(x) defining
respectively the non-membership of the element x to
the set A, which may coexist with the membership
function. More formally the IFS itself is formally
denoted by:
A = {〈x, µ
A
(x), ν
A
(x)〉 | x ∈ E},
and the following conditions hold:
0 ≤ µ
A
(x) ≤ 1, 0 ≤ ν
A
(x) ≤ 1,
0 ≤ µ
A
(x) + ν
A
(x) ≤ 1.
Multiple relations, operations, modal and
topological operators have been defined over IFS,
showing that IFSs are a non-trivial extension of the
concept of fuzzy sets.
The second concept, on which the proposed
method is based, is the concept of index matrix, a
matrix which features two index sets. The basics of
the theory behind the index matrices is described in
(Atanassov, 1991), and recently developed further
on in (Atanassov, 2014).
In the ICA approach, the raw data for processing
are put within an index matrix M of m rows {O
1
, …,
O
m
} and n columns {C
1
, …, C
n
}, where for every p,
q (1 ≤ p ≤ m, 1 ≤ q ≤ n), O
p
in an evaluated object,
C
q
is an evaluation criterion, and e
O
p
C
q
is the
evaluation of the p-th object against the q-th
criterion, defined as a real number or another object
that is comparable according to relation R with all
the rest elements of the index matrix M.
11 1 1 1
1
1
1
1
1, , , ,
,C , , ,
,, ,,
,, ,,
,
kln
iikilin
jjkjljn
mmjmlmn
kln
OC OC OC OC
i O OC OC OC
jOC OC OC OC
mOC OC OC OC
CC CC
M
Oe e e e
Oe e e e
Oe e e e
Oe e e e
=
KKK
KKK
M MOMOMOM
KKK
M MOMOMOM
KKK
M MOMOMOM
KKK
From the requirement for comparability above, it
follows that for each i, j, k it holds the relation
R(e
O
i
C
k
, e
O
j
C
k
). The relation R has dual relation
R
,
which is true in the cases when relation R is false,
and vice versa.
For the needs of our decision making method,
pairwise comparisons between every two different
criteria are made along all evaluated objects. During
the comparison, it is maintained one counter of the
number of times when the relation R holds, and
another counter for the dual relation.
Let
,kl
S
μ
be the number of cases in which the rel-
ations R(e
O
i
C
k
, e
O
j
C
k
) and R(e
O
i
C
l
, e
O
j
C
l
) are simul-
taneously satisfied. Let also
,kl
S
ν
be the number of
cases in which the relations R(e
O
i
C
k
, e
O
j
C
k
) and its dual
R
(e
O
i
C
l
, e
O
j
C
l
) are simultaneously satisfied. As the total
number of pairwise comparisons between the object is
m(m – 1)/2, it is seen that there hold the inequalities:
,,
(1)
0
2
kl kl
mm
SS
μν
−
≤+≤
.
For every k, l, such that 1 ≤ k ≤ l ≤ m, and for
m ≥ 2 two numbers are defined:
,,
,,
2,2
(1) (1)
kl kl
kl kl
CC CC
SS
mm mm
μν
μν ==
−
−
.
The pair, constructed from these two numbers,
plays the role of the intuitionistic fuzzy evaluation of
the relations that can be established between any two
criteria C
k
and C
l
. In this way the index matrix M
that relates evaluated objects with evaluating criteria
can be transformed to another index matrix M* that
gives the relations among the criteria:
11 11 1 1
11
1
1,C,C ,C,C
,C ,C ,C ,C
*
.
,,
,,
nn
n n nn nn
n
CC C C
nCC CC
CC
M
C
C
μν μν
μν μν
=
K
K
MMOM
K
InterCriteria Analysis Applied to Various EU Enterprises
285

From practical considerations, it has been more
flexible to work with two index matrices M
μ
and M
ν
,
rather than with the index matrix M
*
of IF pairs.
The final step of the algorithm is to determine
the degrees of correlation between the criteria,
depending on the user’s choice of µ and ν. We call
these correlations between the criteria: ‘positive
consonance’, ‘negative consonance’ or ‘dissonance’.
Let α, β ∈ [0; 1] be the threshold values, against
which we compare the values of µ
C
k
,C
l
and ν
C
k
,C
l
. We
call that criteria C
k
and C
l
are in:
• (α, β)-positive consonance, if µ
C
k
,C
l
> α and
ν
C
k
,C
l
< β;
• (α,
β)-negative consonance, if µ
C
k
,C
l
< β and
ν
C
k
,C
l
> α;
• (α, β)-dissonance, otherwise.
The approach is completely data driven, and each
new application would require taking specific
threshold values α, β that will yield reliable results.
3 DATA PROCESSING
Here we dispose of and analyse the following input
datasets from (Calogirou, et al., 2010):
• The number of enterprises in EU27, by country,
divided to the four categories: Micro, Small,
Medium and Large (p. 16, Table 4)
• The number of persons employed in EU27, by
country, divided to the four categories: Micro,
Small, Medium and Large (p. 18, Table 6)
• The Turnover (millions of €) in the EU27, by
country, divided to the four categories: Micro,
Small, Medium and Large (p. 20, Table 8)
• Value added at factor cost (millions of €), by
country, divided to the four categories: Micro,
Small, Medium and Large (p. 22, Table 10).
These four source datasets we rearrange in a way
to discover for each of the four indicators: ‘Number
of enterprises (NE)’, ‘Number of persons employed
(PE)’, ‘Turnover (TO)’ and ‘Value added at factor
cost (VA)’ what are the correlations between them
in the different scale, given by the type of
enterprises: ‘Micro’, ‘Small’, ‘Medium’ and ‘Large’.
During this processing, we remove both the rows
and the columns titled ‘Total’ and ‘Pct’, and remain
to work only with the data countries by indicators,
that are homogeneous in nature.
In these new 4 processed datasets (Tables 1–4),
for each type of enterprise, we have one index
matrix with 27 rows being the countries in the
EU27, and 4 columns for the four indicators.
The data from Tables 1–4 concerning the micro,
small, medium and large enterprises, have been
analysed using a software application for Inter-
Criteria Analysis, developed by one of the authors,
Mavrov (Mavrov, 2014). The application follows the
algorithm for ICA and produces from the matrix of
27 rows of countries (objects per rows) and 4
indicators (criteria per columns), two new matrices,
containing respectively the membership and the non-
membership parts of the IF pairs that form the IF
positive, negative consonance and dissonance
relations between each pair of criteria, In this case,
the 4 criteria form 6 InterCriteria pairs.
Table 1: Data for the microenterprises in the EU27
countries, as evaluated against 4 criteria (in %).
EU Member NE PE TA VO
Austria
88 25 18 19
Belgium
92 30 21 19
Bulgaria
88 22 20 14
Cyprus
92 39 30 31
Czech Rep.
95 29 18 19
Denmark
87 19 23 28
Estonia
83 20 25 21
Finland
93 24 16 19
France
92 38 19 21
Germany
83 23 12 16
Greece
96 25 35 35
Hungary
94 58 21 18
Ireland
82 35 12 12
Italy
95 20 28 33
Latvia
83 47 23 19
Lithuania
88 23 13 12
Luxembourg
87 19 18 24
Malta
96 22 22 21
Netherlands
90 34 15 20
Poland
96 29 23 18
Portugal
95 39 26 24
Romania
88 42 16 14
Slovakia
76 21 13 13
Slovenia
93 25 20 20
Spain
92 28 23 27
Fifth International Symposium on Business Modeling and Software Design
286

Sweden
94 15 18 20
United Kingdom
87 22 14 18
Table 2: Data for the small enterprises in the EU27
countries, as evaluated against 4 criteria (in %).
EU Member NE PE TA VO
Austria
11 23 23 20
Belgium
7 22 20 20
Bulgaria
9 24 21 18
Cyprus
7 25 29 26
Czech Rep.
4 19 18 16
Denmark
11 22 22 21
Estonia
14 25 29 25
Finland
6 28 14 16
France
6 26 19 19
Germany
14 19 16 18
Greece
3 21 23 20
Hungary
5 17 18 16
Ireland
15 19 20 17
Italy
5 26 23 23
Latvia
14 22 28 27
Lithuania
9 25 24 23
Luxembourg
11 24 24 20
Malta
4 28 22 20
Netherlands
8 20 21 21
Poland
3 21 13 12
Portugal
5 12 23 22
Romania
9 23 21 16
Slovakia
19 20 16 15
Slovenia
6 21 19 19
Spain
7 18 24 24
Sweden
5 18 18 18
United Kingdom
10 18 16 16
Table 3: Data for the medium enterprises in the
EU27 countries, as evaluated against 4 criteria (in %).
EU Member NE PE TA VO
Austria
2 19 22 21
Belgium
1 16 19 19
Bulgaria
2 24 22 21
Cyprus
1 20 24 21
Czech Rep.
1 20 24 20
Denmark
2 19 22 19
Estonia
3 21 28 30
Finland
1 26 18 18
France
1 15 17 16
Germany
2 18 20 19
Greece
0 16 19 17
Hungary
1 12 19 18
Ireland
3 16 25 23
Italy
1 23 20 16
Latvia
3 12 28 28
Lithuania
2 26 27 29
Luxembourg
2 23 17 19
Malta
1 26 26 23
Netherlands
1 20 26 21
Poland
1 17 23 22
Portugal
1 19 22 21
Romania
2 16 21 20
Slovakia
4 23 21 18
Slovenia
1 18 24 21
Spain
1 21 20 17
Sweden
1 23 19 18
United Kingdom
2 15 18 17
Table 4: Data for the large enterprises in the EU27 countries,
as evaluated against 4 criteria (in %).
EU Member NE PE TA VO
Austria
0.3 33 37 40
Belgium
0.2 33 39 42
Bulgaria
0.3 30 37 46
Cyprus
0.2 17 17 21
Czech Rep.
0.2 32 41 45
Denmark
0.3 40 33 32
InterCriteria Analysis Applied to Various EU Enterprises
287

Estonia
0.4 34 18 24
Finland
0.3 22 52 46
France
0.2 22 44 45
Germany
0.5 41 52 47
Greece
0.1 38 23 28
Hungary
0.2 13 41 48
Ireland
0.5 29 43 48
Italy
0.1 32 29 28
Latvia
0.3 19 20 26
Lithuania
0.3 25 35 36
Luxembourg
0.4 33 42 37
Malta
0.1 24 30 36
Netherlands
0.3 26 38 38
Poland
0.2 33 41 48
Portugal
0.1 31 30 32
Romania
0.4 18 41 50
Slovakia
1.0 36 50 54
Slovenia
0.3 36 37 40
Spain
0.1 33 33 32
Sweden
0.2 44 44 44
United Kingdom
0.4 45 51 49
Because of the diverse nature of the types of
enterprises (micro, small, medium or large enter-
prises), it is expected that these six InterCriteria
pairs will be different depending on which kind of
enterprises are taken into consideration.
Thus, for the micro enterprises, for which are the
data in Table 1, the two index matrices with Inter-
Criteria pairs are respectively given in Table 5, for
the small enterprises the two index matrices are
given in Table 2 – in Table 6, for the medium
enterprises, for which are the data in Table 3, the
two index matrices are given in Table 7, and for the
large enterprises for which are the data are in Table
4, the two index matrices are given in Table 8.
Respectively, the InterCriteria correlation pairs
for small, medium and large enterprises are given in
Tables 5–8. We can immediately note the similar
patterns in the conditional formatting of the eight
tables in Tables 5–8, which are highlighted in a way
to outline the highest possible positive consonances.
Table 5: InterCriteria pairs in micro enterprises.
μ
NE PE TO VA
ν
NE PE TO VA
NE
1.000 0.504 0.621 0.584
NE
0.000 0.396 0.256 0.285
PE
0.504 1.000 0.496 0.413
PE
0.396 0.000 0.425 0.493
TO
0.621 0.496 1.000 0.735
TO
0.256 0.425 0.000 0.160
VA
0.584 0.413 0.735 1.000
VA
0.285 0.493 0.160 0.000
Table 6: InterCriteria pairs in small enterprises.
μ
NE PE TO VA
ν
NE PE TO VA
NE
1.000 0.436 0.533 0.484
NE
0.000 0.447 0.362 0.387
PE
0.436 1.000 0.567 0.527
PE
0.447 0.000 0.319 0.342
TO
0.533 0.567 1.000 0.803
TO
0.362 0.319 0.000 0.077
VA
0.484 0.527 0.803 1.000
VA
0.387 0.342 0.077 0.000
Table 7: InterCriteria pairs in medium enterprises.
μ
NE PE TO VA
ν
NE PE TO VA
NE
1.000 0.316 0.433 0.456
NE
0.000 0.299 0.222 0.182
PE
0.316 1.000 0.516 0.467
PE
0.299 0.000 0.376 0.385
TO
0.433 0.516 1.000 0.781
TO
0.222 0.376 0.000 0.088
VA
0.456 0.467 0.781 1.000
VA
0.182 0.385 0.088 0.000
Table 8: InterCriteria pairs in large enterprises.
μ
NE PE TO VA
ν
NE PE TO VA
NE
1.000 0.453 0.578 0.567
NE
0.000 0.328 0.242 0.248
PE
0.453 1.000 0.527 0.481
PE
0.328 0.000 0.399 0.450
TO
0.578 0.527 1.000 0.829
TO
0.242 0.399 0.000 0.120
VA
0.567 0.481 0.829 1.000
VA
0.248 0.450 0.120 0.000
4 RESULTS AND DISCUSSION
Following a recent idea about analysis of the results
of application of the ICA approach, described in
(Atanassova, 2015), we can interpret the IF pairs,
representing the membership and the non-member-
ship parts of the InterCriteria correlation, as coord-
inates of points in the IF interpretation triangle,
(Atanassov, 1989).
Fifth International Symposium on Business Modeling and Software Design
288

We will note for the interested reader, that
the intuitionistic fuzzy interpretation triangle, see
Figure 1, is the IFS-specific graphical interpretation
of IFSs, which is not available for graphical interpre-
tation of the ordinary fuzzy sets, defined by Zadeh.
The triangle is part of the Euclidean plane, with
vertices the points (0, 0), (1, 0) and (0, 1), staying
respectively for the complete uncertainty, complete
truth and complete falsity as the boundary values
with which elements of an IFS can be evaluated. The
hypotenuse corresponds to the graphical inter-
pretation of the [0, 1]-interval, and points belonging
to it are elements of a classical fuzzy set.
In this interpretation, we can plot the 24 resultant
points onto a single IF triangle: 6 InterCriteria
correlation points for the 4 types of enterprises.
Since we are interested in the highest InterCriteria
correlations, in these terms, it means finding the
points, which are closest to the complete truth in
point (1, 0), which is equivalent to having their
membership parts greater than a given threshold
value
α , and, simultaneously, their non-membership
parts less than a second threshold value
β . For each
of the points, i.e. for each of the correlations
between two different criteria C
i
and C
j
, i ≠ j, we
can calculate its distance from the (1, 0) point,
according to the simple formula:
22
,
(1 )
i j ij ij
C C CC CC
d μν =− +
The results are given in Table 9, and presented
sorted in ascending order according to the distance.
Table 9: Ranking the InterCriteria pairs
by distance to Truth (1, 0).
Enterprise
type
C
i
C
j
μ
CiCj
ν
CiCj
d
CiCj
Large TO VA 0.829 0.120 0.209
Small TO VA 0.803 0.077 0.212
Medium TO VA 0.781 0.088 0.236
Micro TO VA 0.735 0.160 0.310
Micro
N
E TO 0.621 0.256 0.457
Large
N
E TO 0.578 0.242 0.486
Large
N
E VA 0.567 0.248 0.499
Micro
N
E VA 0.584 0.285 0.504
Small PE TO 0.567 0.319 0.538
Medium
N
E VA 0.456 0.182 0.574
Small PE VA 0.527 0.342 0.584
Small
N
E TO 0.533 0.362 0.591
Medium
N
E TO 0.433 0.222 0.609
Medium PE TO 0.516 0.376 0.613
Large PE TO 0.527 0.399 0.619
Micro
N
E PE 0.504 0.396 0.635
Large
N
E PE 0.453 0.328 0.638
Small
N
E VA 0.484 0.387 0.645
Medium PE VA 0.467 0.385 0.658
Micro PE TO 0.496 0.425 0.659
Large PE VA 0.481 0.450 0.687
Small
N
E PE 0.436 0.447 0.720
Medium
N
E PE 0.316 0.299 0.746
Micro PE VA 0.413 0.493 0.767
We can, then, make two rounds of discussions.
On one hand, see Figure 1, we can seek and for-
mulate some assumptions about the InterCriteria
correlations with respect to the type of enterprise.
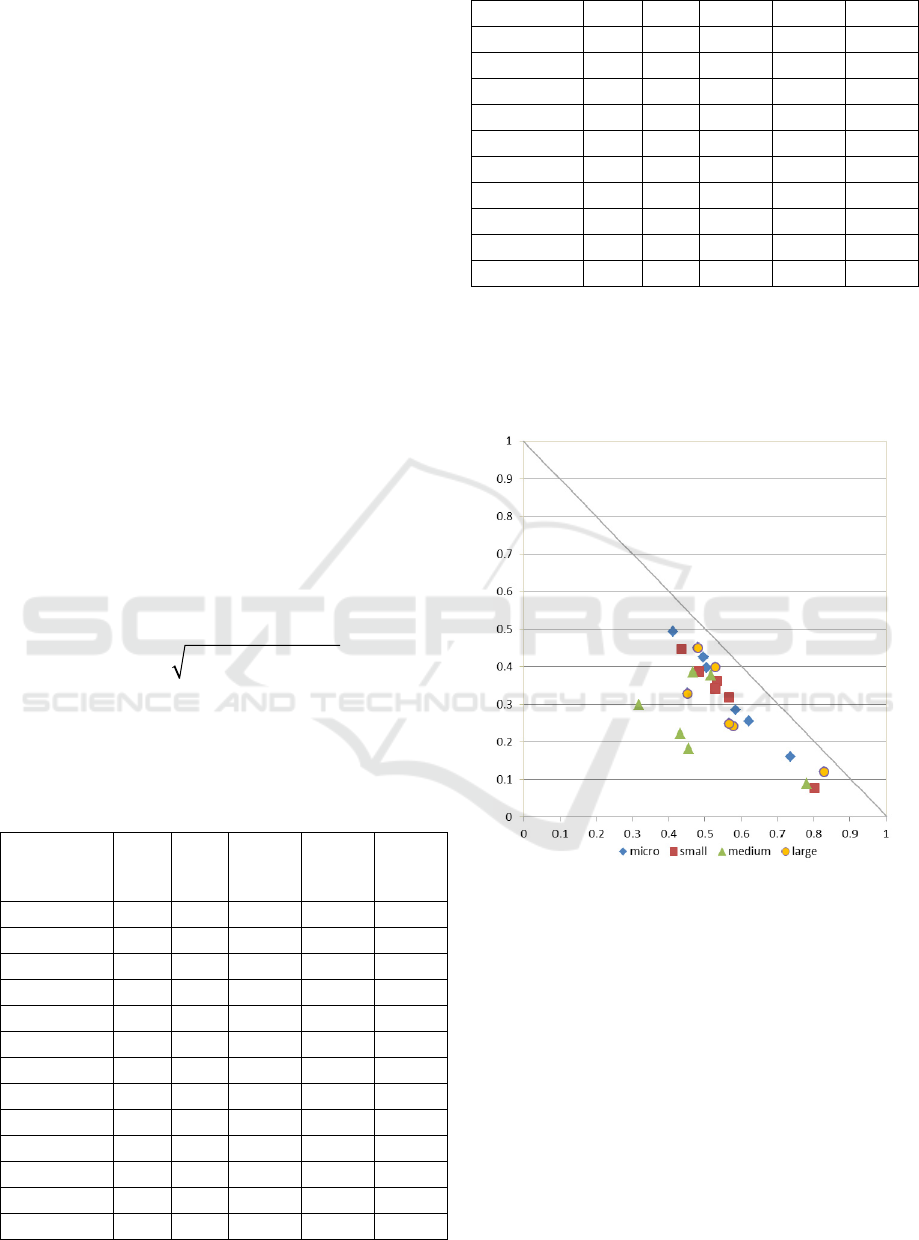
Figure 1: ICA results with respect
to the type of enterprise.
We can notice from here that micro and small
enterprises exhibit very similar patterns of Inter-
Criteria consonance, with all the InterCriteria pairs
exhibiting relatively low levels of uncertainty, and
only the pair TO/VA exhibiting relatively high
positive consonances. The same pair ranges highest
among the InterCriteria correlations with the other
two types of enterprises, medium and large. The
large type of enterprises also exhibits relatively low
uncertainty in the InterCriteria correlations, being
lowest with TO/VA, PE/TO and PE/VA, and highest
uncertainty featured in the rest three of the pairs.
Expectedly, the most scattered is the pattern with the
InterCriteria Analysis Applied to Various EU Enterprises
289

medium type of enterprises, where also the largest
uncertainty is observed, all in the pairs containing
the number of enterprises: NE/PE, NE/TO and
NE/VA.
On the other hand, it is considered appropriate
to analyse these 24 points as 6 groups of 4 points,
grouped according to the criteria in the pair
(Figure 2). We can then make some assumptions
about the nature of these correlations, judging from
how concentrated or how scattered the four points in
each group are: the more concentrated the points for
a given InterCriteria pair, the more consistent beha-
viour of this pair across the different scales of
economic entities.
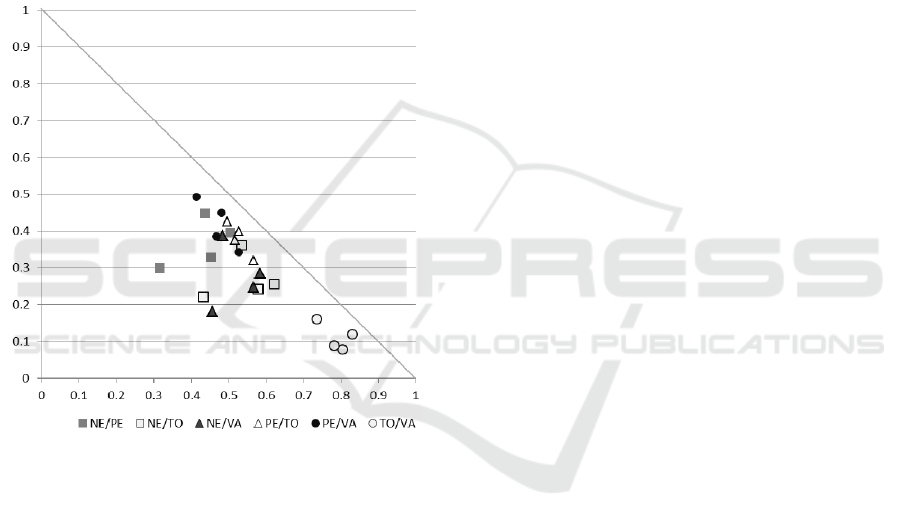
Figure 2: ICA results with respect
to correlations between economic indicators.
We will immediately note what was visible from
the Table 9, that that the pair of criteria TO/VA are
distinctly best correlating across the different scales
of economic entities, concentrated in the closest
proximity to the absolute truth represented by the
(1, 0) point. It is interesting however to note other,
less clearly seen relations. For instance, we can note
that quite similar patterns are formed for the two
four-point sets corresponding to the pairs of criteria
PE/VA and PE/TO: relatively parallel and closely
located to the hypothenuse. In both these pairs, the
distances from the (1, 0) point, according to the type
of enterprise, follow in decreasing order the se-
quence: ‘small’ – ‘medium’ – ‘large’ – ‘micro’, with
medium and large enterprises exhibiting very close
results. Quite similar and closely located to each
other are also the patterns for the pairs of criteria
NE/TO and NE/VA.
These three observations over these particular
economic data lead us to the speculation that from
theoretical point of view it would be interesting to
pay attention to situations when we have two criteria
C
i
, C
j
that exhibit high positive consonance with
each other, and each of them exhibit similar or
identical consonance patterns in the pairs C
i
–C
k
and
C
j
–C
k
, or vice versa, if C
i
–C
k
and C
j
–C
k
are two pairs
of criteria with high positive consonances, would
there be high positive consonance in the pair C
i
–C
j
.
This question would be worth exploring in the light
of the possibility to detect, using ICA not just pairs
of correlating criteria, but also triplets, etc.
5 CONCLUSION
The present research analysed data about the micro,
small, medium and large economic entities in the
EU27, as evaluated against four economic indicators
(criteria). The utilised method for analysis of the
datasets was the novel decision support approach,
called InterCriteria Analysis. The results are two-
fold: they outline correlations between economic in-
dicators on these four levels of economic enterprise,
new thus potentially brining new knowledge and
understanding, and also contribute to elaboration of
certain aspects of the methodology of ICA.
ACKNOWLEDGEMENTS
The research work reported in the paper is partly
supported by the project AComIn “Advanced
Computing for Innovation”, Grant №316087, funded
by the FP7 Capacity Programme (Research Potential
of Convergence Regions) and partly supported under
the Project № DFNI-I-02-5/2014 “InterCriteria
Analysis – A New Method for Decision Making”.
REFERENCES
Atanassov K. (1983). Intuitionistic fuzzy sets, VII
ITKR's Session, Sofia, June 1983 (in Bulgarian).
Atanassov K. (1986). Intuitionistic fuzzy sets. Fuzzy
Sets and Systems. vol. 20 (1), pp. 87–96.
Atanassov K. (1989). Geometrical interpretations of
the elements of the intuitionistic fuzzy objects.
Pre-print IM-MFAIS-1-89, Sofia.
Fifth International Symposium on Business Modeling and Software Design
290

Atanassov K. (1991). Generalized nets. World
Scientific, Singapore.
Atanassov K. (1999). Intuitionistic Fuzzy Sets: The-
ory and Applications. Springer Physica-Verlag,
Heidelberg.
Atanassov K. (2012). On Intuitionistic Fuzzy Sets
Theory. Springer, Berlin.
Atanassov K. (2014). Index Matrices: Towards an
Augmented Matrix Calculus. Springer, Cham.
Atanassov K., D. Mavrov, V. Atanassova (2014).
InterCriteria decision making. A new approach
for multicriteria decision making, based on index
matrices and intuitionistic fuzzy sets. In: Issues
in Intuitionistic Fuzzy Sets and Generalized
Nets, vol. 11, pp. 1–8.
Atanassova V. (2015). Interpretation in the Intui-
tionistic Fuzzy Triangle of the Results, Obtained
by the InterCriteria Analysis, IFSA-EUSFLAT
Conference, 29 June – 3 July 2015, Gijon, Spain
(to appear).
Atanassova V., L. Doukovska, K. Atanassov, D.
Mavrov (2014). InterCriteria Decision Making
Approach to EU Member States Competitiveness
Analysis. Proc. of 4th International Symposium
on Business Modeling and Software Design, 24–
26 June 2014, Luxembourg, pp. 289–294.
Atanassova V., D. Mavrov, L. Doukovska, K.
Atanassov (2014). Discussion on the threshold
values in the InterCriteria Decision Making
approach. Notes on Intuitionistic Fuzzy Sets, vol.
20 (2), pp. 94–99.
InterCriteria Research Portal,
http://www.intercriteria.net/publications.
Calogirou C., S. Y. Sørensen, P. B. Larsen, S.
Alexopoulou, et al. (2010). SMEs and the
environment in the European Union, PLANET
SA and Danish Technological Institute, Pub-
lished by European Commission, DG Enterprise
and Industry.
InterCriteria Analysis Applied to Various EU Enterprises
291