Design of a Real Coded GA Processor

A. Tsukahara and A. Kanasugi

Graduate School of Science and Engineering, Tokyo Denki University 5 Senju-Asahi-cho, Adachi-ku, Tokyo, Japan

Keywords: Generic Algorithm, Real Coded Generic Algorithm, FPGA.

Abstract: Real Coded Genetic Algorithm (RCGA) has been attracting attention as one of the GA for handling real-

valued vectors. Various GA hardware have been proposed, for evolvable hardware, and for an increase in

computational throughput. Yet, there are few reports of RCGA hardware. Herein, we propose a design for a

real coded GA processor. The proposed processor is implemented using the JGG (Just Generation Gap) as a

generation alternation model and the REX (Real coded Ensemble Crossover) as a crossover. In addition, the

evaluation functions that depend on problem are calculated using soft macro CPU. The proposed processor

is to be applied expected in embedded field applications because of it can be implemented in one chip

FPGA.

1 INTRODUCTION

Many engineering problems have no known

solution, or impose a large computational cost.

Heuristic approaches are often effective for such

difficult problems. That is, the search for

approximate solutions, having sufficiently practical

accuracy, occurs within an acceptable time, by the

use of an empirical method. One such approach is

genetic algorithm (GA). GA is based on the idea of

the evolution of life; it is one of the optimization

algorithms. GA can be applied to various problems,

such as combinatorial optimization problem and NP-

hard problem. Moreover, GA has affinity with

evolvable hardware which has been attracting

attention. Real Coded Genetic Algorithm (RCGA)

has been attracting attention (Kobayashi, 2009). It is

handling real-valued vectors as genotype. RCGA is

much better than conventional GA, when handling

the genotype within a bit strings. Therefore, it is also

effective for high-dimensional problem.

In case of usual PC require long calculation time,

a dedicated hardware is effective. Various GA

hardware have been proposed based on conventional

GA (Fernaldo et al., 2010). These GA hardwares are

used evolvable hardware as one of applications. The

evolvable hardware is a device to change optimum

hardware configuration by evolutionary computation.

For example, there are applications such as the

image filter circuit (Vasicek et al., 2007). However,

there are few reports of RCGA hardware.

In this paper, we propose a design of RCGA

processor. The proposed processor is implemented

using the JGG as a generation alternation model and

the REX as a crossover. Effective sharing of

computing units reduce the circuit scale.

Furthermore, the use of soft macro CPU enhance

versatility. The proposed processor is expected in

embedded field applications because of it can be

implemented in one chip FPGA.

2 REAL-CODED GA

The main processing of RCGA consists of a

generation alternation model and a crossover. The

generation alternation model consists of a

reproduction selection and a survival selection of

individuals.

Several generation alternation model have been

proposed such as MGG (Minimal Generation Gap)

and JGG (Just Generation Gap) (Akimoto et al,

2007). The two parents are selected in MGG. On the

other hand, more than two parents are selected in

JGG. The better results are often obtained by using

JGG than MGG.

Several crossover mechanisms in RCGA have

been proposed. Among them, The Real coded

Ensemble Crossover (REX) (Kobayashi, 2009) has

good performance with low computational cost.

Therefore, the proposed processor is implemented

using the JGG and the REX.

334

Tsukahara, A. and Kanasugi, A..

Design of a Real Coded GA Processor.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 1: ECTA, pages 334-339

ISBN: 978-989-758-157-1

The JGG perform three steps (Akimoto et al,

2007) below.

(1) Reproduction selection: The Np number of

individuals are extracted with non-restoring

at random from the population.

(2) Generating Offspring: The Nos number of

offspring are generated repeatedly applying

crossover by using the parents.

(3) Survival selection: The top Np number of

individuals are selected in accordance with

evaluation value from the offspring.

In the above steps, Np and Nos are the number of

parent (two or more) and the number of offspring,

respectively. These parameters must be carefully

chosen according to the problems. The offspring is

generated according to equation (1) by using the

replicated selected the parents in REX.

 

,0~,





igi

igc

xxxx 







(1)

Where x is a real-valued vector of dimension

number N, x

= {x

, x

, ..., x

N+k

} are the parents, x

the center of gravity of parents and x

is the

offspring. k is set interval, 1 ≤ k ≤ P-N. P is number

of the population. Let

),0(





be the probability

distribution with average 0, dispersion





and

arbitrary symmetry.



is a parameter according to

probability distribution

),0(









is necessary that

)/(1

kN 





be satisfied. In order to satisfy this

equation, let

)/(3 kN 



when using random

number of interval [-α, α] in φ.

The REX requires smaller amount calculation

than such as CMA-ES (Covariance Matrix

Adaptation Evolution Strategy). Since the variance-

covariance matrix is implicitly handled in the REX.

Furthermore, The Adaptive Real-coded Ensemble

Crossover (AREX) (Akimoto et al, 2009) has been

proposed as improving the REX. The AREX is

added mechanism to avoid the initial convergence

that occurs in the optimization of the ridge structure

function and multi-peak function. In addition, Big-

valley Explorer (BE) (Uemura et al, 2011) for multi-

funnel function optimization has been proposed. The

BE is used the AREX and JGG. The BE has been

reported to be better performance than the Multi

Start CMA-ES (That is CMA-ES which initialize the

population in the entire search space) in some

benchmark functions.

3 RCGA PROCESSOR

3.1 Overview of RCGA Processor

In the proposed processor, first, parents are selected

at random in accordance with the JGG. Then, the

offspring are generated by the REX. The evaluations

are started by soft macro CPUs when first offspring

is generated. Moreover, the selection of the offspring

to be saved in the next generation population is also

performed in parallel. Then, the current population is

updated with the new offspring when the evaluation

of all offspring are complete. An optimum solution

is searched by the repetition of these processes.

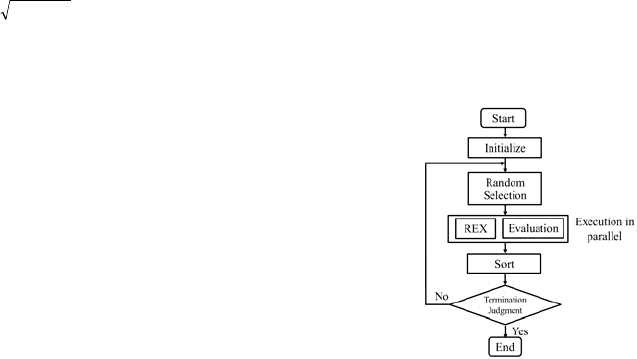
Figure 1 shows a flowchart of the proposed

processor.

There are four parameters to set in the RCGA;

number of dimensions N, number of parents Np,

number of offspring Nos and number of population

P. Np, Nos and P are determined on basis of N. Np

is set as N+k. In the proposed processor, Np is set as

the number of N+2 and number of power of two. Np

is a reference parameter to parallelize the proposed

processor. Therefore, main circuit such as arithmetic

units or CPUs for evaluation exists by Np sets. Nos

is set integer multiple of Np. This integer number is

Nosr. Generation and evaluation of the offspring are

performed in Np parallel. Therefore, the Nos number

of offspring are generated by repeatedly executing

those processes Nosr times. P is set as integer

multiple of N.

The proposed processor can be set several

parameters by one of the CPU. The configurable

parameters are the RCGA parameters, a goal of

fitness to be a termination condition, a number of

evaluations to abort the process.

Figure 1: Flowchart of the proposed processor.

3.2 Detail of Proposed Processor

Figure 2 shows a block diagram of the proposed

RCGA processor. The data are handled as single-

Design of a Real Coded GA Processor

335

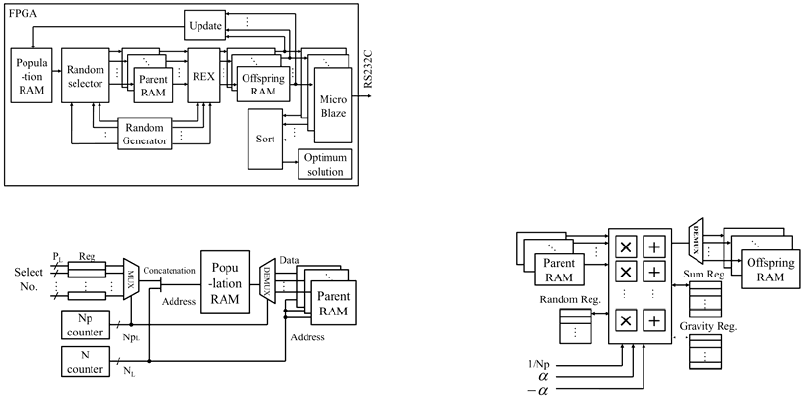
precision floating-point number that conforms to

IEEE754.

The processor consists of the following blocks; (a)

Memory (Population, Parent, Offspring), (b)

Random number generator, (c) Random selection

circuit, (d) REX circuit, (e) Evaluation circuit, (f)

Sorting circuit, (g) Updating circuit.

3.2.1 Memory

Genotype of individual is a real-valued vector with

N dimensions. A population memory store the P

number of individuals. The parent memories and the

offspring memories are prepared Np sets. Each

parent memory store an individual. Each offspring

memory store the Nosr number of individuals. In

population memory and offspring memory, the

upper bits of address are individual number and the

lower bits are each element.

3.2.2 Random Number Generator

This circuits consists of the M-sequence random

number generator and the fixed point number to

floating point number conversion circuits. First, Np

sets of 23 bits random numbers are generated. The

number of bits are corresponded to the mantissa 23

bits of single precision floating point format. Then,

they are outputted after being converted Np number

of fixed point number to floating point number at the

same time. In addition, Np sets of lower log

P bits of

23 bits signal are also used as selected number of

parents in a random selection circuit.

Figure 2: Block diagram of the proposed processor.

Figure 3: Random selection circuit.

3.2.3 Random Selection Circuit

The Np sets of random numbers are obtained from

the random number generator. These are individual

numbers to select as parents from the population

memory. The individual numbers are selected by the

output of Np counter (log

Np bits, Np

). In addition,

this counter select the memory to store among the

Np sets parent memories. The selected numbers and

the output of N counter (log

N bits, N

) are

concatenated. This signal is inputted to the

population memory as an address signal. These data

are stored to the parent memories. The number of

parents are counted once one individual reading is

completed. This circuit halts after all Np sets parents

data are read out. Figure 3 shows a block diagram of

the random selection circuit.

3.2.4 REX Circuit

In the REX circuit, the Nos number of offspring are

generated by performing the calculation of equation

(1). The calculation of the equation (1) is performed

by dividing into the following five steps; (1)

Summation, (2) Calculation of the center of gravity

, (3) Calculation of deviation (x

-x

), (4)

Generation of random numbers (



), (5) Generating

offspring.

Figure 4 shows a block diagram of REX circuit.

This circuit primarily consists of Np sets of single

precision floating point multipliers and adders and

some registers. The pipeline stage of multiplier and

adder are set as four. A feature of this circuit is to

achieve calculations by effectively utilizing the Np

sets of multipliers and adders. The above five steps

are calculated by changing the connection of

multipliers and adders in each state. Therefore, the

circuit can be implemented with less circuit

resources than the case of arithmetic units are

prepared as many as necessary in each state. Figure

5 shows the wiring diagram of arithmetic units at

each state in the case of Np = 4.

Figure 4: REX circuit.

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

336

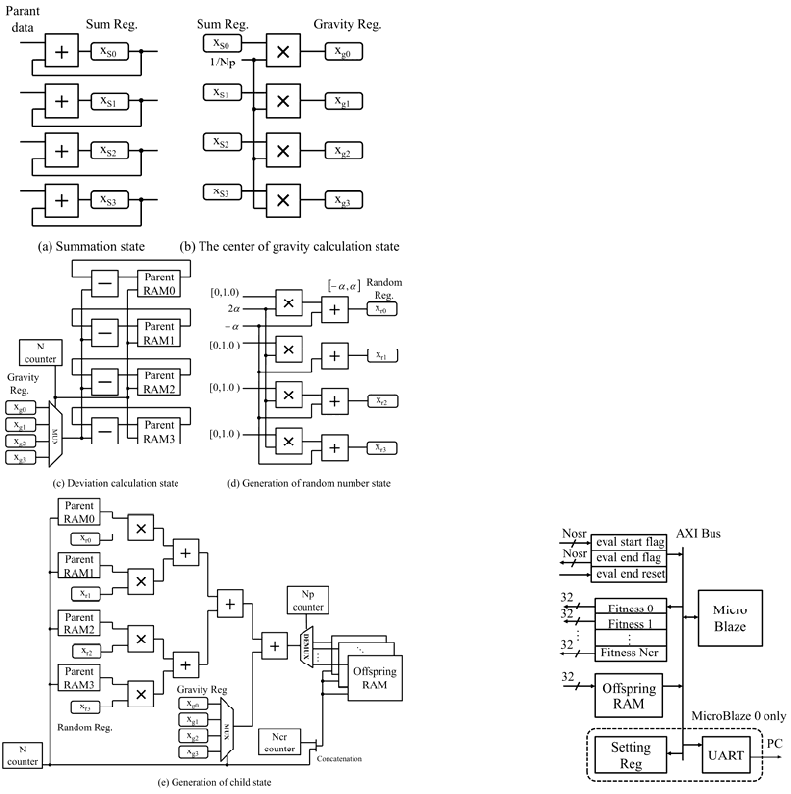
The operations in each state are shown below.

At the step (1), all adders are used in parallel as

shown in Figure 5 (a). Each time of reading data

from the population memory, the data is added and

stored to the sum register in each dimension.

At the step (2), all multipliers are used in parallel

as shown in Figure 5 (b). The x

is calculated by

multiplying a 1/Np in parallel to the sum registers in

each dimension.

At the step (3), all adders are used in parallel as

subtractors as shown in Figure 5 (c). The data are

read simultaneously from Np sets parent memories.

The deviations between the each dimension of the x

and each parents are calculated. The data of parent

memories are overwritten by these deviations.

Figure 5: Wiring diagram of each state (e.g. Np = 4).

The step (1) to (3) are performed only once in a

generation.

At the step (4), all multipliers and adders are

connected and used in parallel as shown in Figure 5

(d). The calculation of 



2



 is performed

in this state. Where R

is random number of [0,1), R

is random numbers of [-α, α]. The generated random

numbers are stored to the random registers.

At the step (5), all multipliers and adders are

used by combining as shown in Figure 5 (e). First,

the result of calculations in step (3) and the random

numbers generated in step (4) are simultaneously

multiplied at the same time. Then, the sum is

calculated by the connecting adders. The one

dimensional data of an offspring is calculated by

adding the x

of the dimension at the adder. The

calculated results are stored in the offspring

memories. The one offspring is generated by

performing the above process N times.

The Nos number of offspring are generated by

execution of Nosr × Np times of step (4) and (5).

3.2.5 Evaluation Circuit

This circuit calculate the fitness of the offspring

generated by the REX in accordance with an

evaluation function. The proposed processor

calculate fitness by the Np sets MicroBlaze (Xilinx

Corporation) soft macro CPU in parallel. Therefore,

it is possible to change the problem by rewriting the

evaluation function of program. The MicroBlaze has

RISC architecture and the 5-stage pipeline. As the

peripheral circuits, evaluation start and end flag

registers, an offspring memory and the

corresponding fitness registers are connected

through an AXI bus. Only one CPU is connected

parameter registers set of the RCGA and a serial

communication module for displaying the final

optimum solution. Figure 6 shows MicroBlaze and

peripheral circuits.

Figure 6: MicroBlaze and peripheral circuit.

The operation of this circuit is as follows. The

evaluation start flag is set whenever an offspring is

Design of a Real Coded GA Processor

337

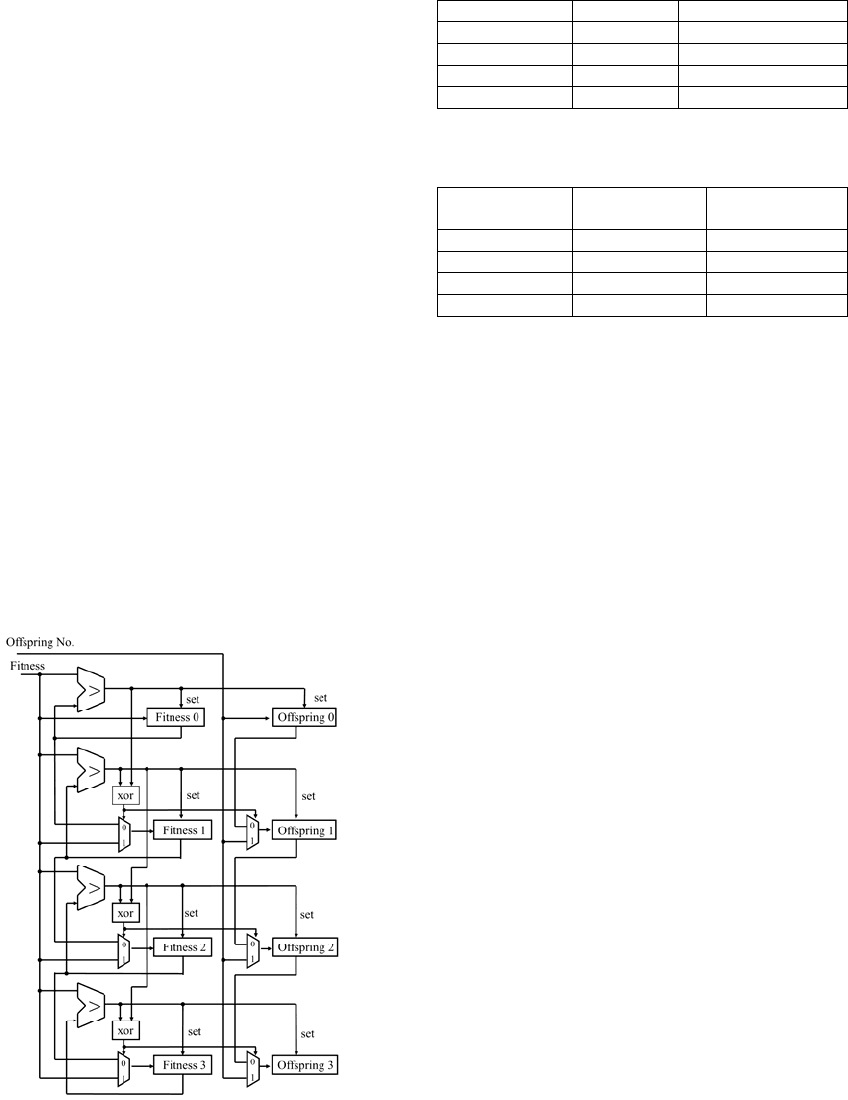
generated by the REX. Then, evaluation calculation

is started. After the calculation, the result data is

stored to the corresponding fitness register. Then,

evaluation end flag is set. It is sequentially evaluated

in parallel with the generation of offspring.

3.2.6 Sorting Circuit

This circuit store the top Np offspring's number

while sorting in ascending order based on the fitness

of each individual to save for the next generation.

This circuit consists of Np sets floating point

comparators, top Np sets fitness registers and the

corresponding offspring number registers. If the

change of evaluation end flag is detected, a new

fitness is compared with simultaneously the current

top Np sets of fitness registers. An insert location of

a new individual is determined by result of exclusive

OR of the comparison results of one level higher.

At this time, the lowest fitness and individual

number are erased. Then, the new fitness and

individual number are inserted into the insertion

location. Since evaluation is parallel with performs

the above processing, top Np sets individuals are

determined because of registers are completed

sorting when the Nos number of the evaluations are

completed. The 0-th individual is a best solution in

current generation. Figure 7 shows a block diagram

of the sorting circuit when Np = 4.

Figure 7: Sorting circuit (e.g. Np=4).

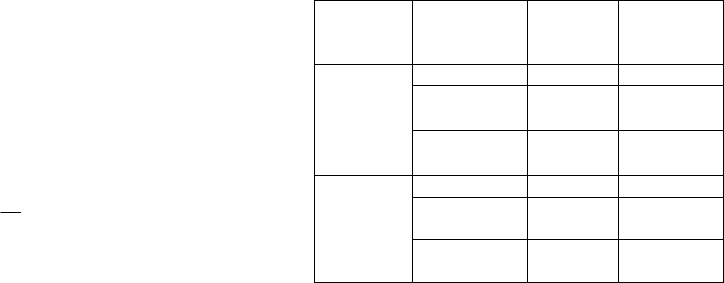
Table 1: The circuit scale of the proposed processor.

FPGA resource XC7A200T Proposed Processor

Slice Register 269200 76102 (28%)

Slice LUT 134600 104162 (78%)

Block RAM 365 161 (44%)

DSP 740 160 (22%)

Table 2: The circuit scale of the RCGA processing, the

MicroBlaze and peripherals.

FPGA resource

RCGA

processing

MicroBlaze and

peripheral

Slice Register 17200 (6%) 58902 (22%)

Slice LUT 26636 (20%) 77525 (58%)

Block RAM 8 (2%) 153 (42%)

DSP 80 (11%) 80 (11%)

3.2.7 Updating Circuit

This circuit update the population memory by the

top Np sets offspring. Hence, the individuals who

have been selected as parents are overwritten by

these offspring. Then, the fitness of current optimum

solution is compared with the fitness of 0-th

offspring in the sorting circuit. The optimum

solution memory is updated when the fitness of 0-th

individual is higher.

4 EXPERIMENT

4.1 Environment and Circuit Scale

The proposed processor was designed using VHDL.

The circuit was synthesized using the PlanAhead

(14.7) of Xilinx Corporation. The circuit was

implemented on the AC701 FPGA evaluation board

of Xilinx Corporation. This board is implemented

the Artix-7(XC7A200T-2FBG676C). Therefore, the

arithmetic units in the REX circuit and the CPUs for

evaluation are implemented 16 sets respectively. The

proposed processor can be implemented in about

80% of the circuit scale on the low-end FPGA. In

addition, Table 2 shows a respective circuit scale of

the RCGA processing circuit, the MicroBlaze and

peripheral circuits. The MicroBlaze and peripheral

circuits occupy more than 50% in the proposed

processor. The RCGA processing circuits are about

20% of the circuit scale. This is considered because

of the floating point arithmetic units are shared.

4.2 Evaluation

The proposed processor was confirmed the

ECTA 2015 - 7th International Conference on Evolutionary Computation Theory and Applications

338

performance by applying to two benchmark

functions. The evaluation functions are the Sphere

function by equation (2) and the Ellipsoid function

by equation (3). The optimum solution of these

functions are the minimum value f(x) = 0. The

optimum solution is obtained when all of the

variables are 0.





xxf

)(

)12.512.5( 

(2)





















xxf

1000)(

)12.512.5( 

(3)

As a comparison, the C language program of

RCGA was implemented and executed on a PC

(Intel (R) Xeon (R) CPU E5-1620, 3.7GHz). The

program was compiled by using the GCC-4.8.2. The

program is not applied parallelism; it is executed on

a single core CPU. After the fitness value f(x) is

reached 10

-7

or less, the x is regarded as an optimum

solution. Table 3 shows the result of each function

on the each environment. The FPGA was operated at

frequency of 100MHz. The results are the average of

30 times performed on the each environment. The

Nos was set to be a close value of integer multiple of

N on the proposed processor. In the Sphere function,

the number of evaluation to reach an optimum

solution is about 18,000 times on the PC at 12.1 ms.

On the other hand, the proposed processor required

about 19,000 times at 12.4 ms. In Ellipsoid function,

the number of evaluation is about 35000 times on

the PC at 27.2 ms, about 38000 times on the

proposed processor at 23.7 ms.

The number of evaluation of proposed processor

was slightly increased, compared with PC. It was

considered that because some part of processing of

proposed hardware simplified for hardware

implementation. Moreover, although the operating

frequency of the PC and the FPGA board are very

different, the execution times are almost the same. If

it is possible to improve the operating frequency of

the proposed processor, it is considered that the

result can be obtained in the execution time of more

than equivalent to the PC.

5 CONCLUSIONS

In this paper, we proposed a design of RCGA

processor. The proposed processor is implemented

using the JGG and the REX. The processor can be

implemented less circuit scale by effectively sharing

the circuit resources such as the arithmetic units. In

addition, the proposed processor has versatility

Table 3: Result of each evaluation function.

Function Item

(Xeon,

3.7GHz)

Proposed

processor

(100MHz)

Sphere

Nos 7N 6Np (≈7N)

Evaluation

number

18813 19302

Execution

time (ms)

12.1 12.4

Ellipsoid

Nos 8N 7Np (≈8N)

Evaluation

number

35737 37811

Execution

time (ms)

27.2 23.7

because the evaluation functions that depend on

problem are calculated using soft macro CPU. The

implementation experiments were evaluated by

using two benchmark functions. The results can be

obtained in almost the same execution time single

core operation on the PC. The proposed processor is

expected in embedded field applications because of

it can be implemented in one chip FPGA.

Future works are to perform the improvement of

running speed and the application of such evolvable

hardware using the proposed processor.

REFERENCES

Kobayashi, S., (2009). The frontiers of real-coded genetic

algorithms, Transactions of the Japanese Society for

Artificial intelligence, 24(1):147-162.

Fernaldo, P., R., Katkoori, S., Keymeulen, D., Zebulum,

R., and Stoica, A., (2010). Customizable FPGA IPcore

implementation of a general-purpose genetic algorithm

engine, IEEE Trans. Evol. Comput., 14(1):133-149.

Vasicek, Z., and Sekanina, L., (2007). Evaluation of a

New Platform For Image Filter Evolution, Adaptive

Hardware and Systems, 2007. AHS 2007. Second

NASA/ESA Conf. on, pages 577-586.

Akimoto, Y., Hasada, R., Sakuma, J., Ono, I., and

Kobayashi, S., (2007). Generation Alternation Model

for Real-coded GA Using Multi-Parent Proposal and

Evaluation of Just Generation Gap (JGG), SICE

Symposium on Decentralized Autonomous Systems,

19:341-346.

Akimoto, Y., Sakuma, J., Ono, I., and Kobayashi, S.,

(2009). Adaptation of expansion rate for real-coded

crossovers, Proceedings of the 11th Annual conference

on Genetic and evolutionary computation. ACM,

pages: 739-746.

Uemura, K., Kinoshita, S., Nagata, Y., and Kobayashi, S.,

and Ono, I., (2011). A new framework taking account

of multi-funnel functions for Real-coded Genetic

Algorithms. In Evolutionary Computation (CEC),

2011 IEEE Congress on. IEEE, pages 2091-2098.

Design of a Real Coded GA Processor

339