Bayesian Logistic Regression using Vectorial Centroid for Interval

Type-2 Fuzzy Sets

Ku Muhammad Naim Ku Khalif and Alexander Gegov

School of Computing, University of Portsmouth, Portsmouth, PO1 3HE, U.K.

Keywords: Interval Type-2 Fuzzy Sets, Uncertainty, Defuzzification, Vectorial Centroid, Machine Learning, Bayesian

Logistic Regression, Human Intuition.

Abstract: It is necessary to represent the probabilities of fuzzy events based on a Bayesian knowledge. Inspired by

such real applications, in this research study, the theoretical foundations of Vectorial Centroid of interval

type-2 fuzzy sets with Bayesian logistic regression is introduced. This includes official models, elementary

operations, basic properties and advanced application. The Vectorial Centroid method for interval type-2

fuzzy set takes a broad view by exampled labelled by a classical Vectorial Centroid defuzzification method

for type-1 fuzzy sets. Rather than using type-1 fuzzy sets for implementing fuzzy events, type-2 fuzzy sets

are recommended based on the involvement of uncertainty quantity. It also highlights the incorporation of

fuzzy sets with Bayesian logistic regression allows the use of fuzzy attributes by considering the need of

human intuition in data analysis. It is worth adding here that this proposed methodology then applied for

BUPA liver-disorder dataset and validated theoretically and empirically.

1 INTRODUCTION

Uncertainty problems are frequently described in

complex systems. In dealing with uncertainty, a lot

of techniques have drawn the attentions of

researchers and applied scientists over last decade.

Decisions are made based on information given

which known as data. However, information about

decision is always uncertain. In real-world

phenomena, the uncertain information may consist

of randomness, vagueness and fuzziness. Machine

learning has always been considered as an integral

part of the field of artificial intelligence. In artificial

intelligence research area, the main problems that

always arise are: how to represent the uncertain

information precisely: and how to reason using

uncertain information (Tang et al., 2002). Machine

learning is certainly one of the most significant

subfields of modern artificial intelligence. In recent

years, machine learning systems have been adopted

standard framework to deal with imprecision in data

analysis.

In describing imprecise, type-1 fuzzy sets are

used as a tool to erase these imprecision properly.

Uncertainty is closely related with probability,

which establishes the formal framework in machine

learning systems. Uncertainty and fuzziness are

well-known phenomena in many application areas in

science and engineering, where are often not crisp

but there exist various degree of membership grade

that practical automatically occurs in machine

learning. Type-2 fuzzy sets are suitable for

uncertainty or approximate reasoning, especially for

the machine learning systems with a mathematical

model that is difficult to derive. Klir and Yuan

(1995) claim that type-1 fuzzy sets only describe

imprecise not uncertainty. On particular motivation

for the further interest in type-2 fuzzy sets that its’

provide a better scope for modelling uncertainty than

type-1 fuzzy sets (Wagner and Hagras, 2010).

In the literature of fuzzy sets, Zadeh (1965) was

introduced fuzzy set theory in representing

vagueness or imprecision in a mathematical

approach. In order to do so, the main motivation of

using fuzzy sets shows its ability in appropriately

dealing with imprecise numerical quantities and

subjective preferences of decision makers (Deng,

2013). According to Zimmermann (2000), he claims

that the fuzzy numbers are represented as possibility

distribution where most of the real-world

phenomena that exist in nature are fuzzy rather than

probabilistic or deterministic. Fuzzy set theory was

specifically designed to mathematically represent to

uncertainty and vagueness. It also provide

formalised tools for dealing with imprecision

Khalif, K. and Gegov, A..

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets.

In Proceedings of the 7th International Joint Conference on Computational Intelligence (IJCCI 2015) - Volume 2: FCTA, pages 69-79

ISBN: 978-989-758-157-1

essential to many real problems nowadays.

Technologies nowadays have been developed in

fuzzy sets that have potential to support all of the

steps that encompass a process of model orientation

and knowledge discovery. In particular, fuzzy sets

theory can be used in data analysis to model vague

data in terms of fuzzy sets. There are some

contributions that fuzzy sets can make to machine

learning which are: 1) graduality; 2) granulity; 3)

interpretability; 4) robustness; 5) representation of

uncertainty; 6) incorporation of background

knowledge and; 7) aggregation, combination, and

information fusion (Hullermeier, 2011).

The concept of type-2 fuzzy set was introduced

by Zadeh (1975) as an extension of the type-1 fuzzy

set. According to Karnik and Mendel (2001), they

claim that type-2 fuzzy set can be characterised as

fuzzy membership function where the membership

value for each element in type-2 is a fuzzy set in

[0,1], unlike type-1 where the membership value is a

crisp value in [0,1]. The interval type-2 fuzzy sets

are widely used type-2 fuzzy sets in many practical

science and engineering areas (Mendel et al., 2006).

The involvement of higher level uncertainty of type-

2 fuzzy sets compared to type-1, provide additional

degrees of freedom to represent the uncertainty and

the fuzziness of real world problems. There are two

types of uncertainty which are inter and intra

personal uncertainties, in improvising the

representation of type-1 fuzzy sets in the literature of

fuzzy sets. This is also supported by Wallsten and

Budescu (1995) where there are supposedly two

kinds of uncertainties that are related to linguistic

characteristics namely intra-personal uncertainty and

inter-personal uncertainty. In particular, a lot of

experts have applied interval type-2 fuzzy sets in

machine learning systems analysis. Due to

implementing interval type-2 fuzzy sets in real

problems, the way to handle is different and much

more complex compared to type-1 fuzzy sets. The

contribution of centroid of type-2 fuzzy sets till now

commonly-used uncertainty measure for modelling

problems.

The implementation of defuzzification plays an

important role in the performance of fuzzy system’s

modelling techniques (Yager and Filev, 1994).

Defuzzification process is guided by the output

fuzzy subset that one value would be selected as a

single crisp value as the system output. There are

variety defuzzification methods have largely

developed, however they have difference

performances in difference applications and there is

a general method can satisfactory performance in all

conditions (Mogharreban and Dilalla, 2006). The

centroid defuzzification methods of fuzzy numbers

have been explored for the last decade that

commonly used and have been applied in various

discipline areas. The computation complexity of

type-2 fuzzy set is very difficult to handle into

practical applications because of characterised by

their footprint of uncertainty (Mendel, 2001). There

are two typical paths in computing type-2 fuzzy sets

which are: 1) type-reduction (Karnik and Mendel,

2001), (Mendel, 2001) (Liu, 2008) and; 2) direct

defuzzification (Gong et al., 2015). Most experts

applied type-reduction methods in handling the

complexity of type-2 fuzzy sets by finding

equivalent type-1 fuzzy sets. However, direct

defuzzification for type-2 fuzzy sets is still under

study.

The concept of possibility mean value for

interval fuzzy sets was introduced by Carlsson and

Fuller (2001) where the notations of lower

possibilistic and upper possibilistic mean values is

defined the interval-valued possibilistic mean. From

probabilistic viewpoint, the possibility mean value

of fuzzy sets can be represented as expected values

which is same function as direct defuzzification

method where it doesn’t need type-reduction stage to

get the outputs. Gong et al. (2015) extends the

concept of Carlsson and Fuller (2001) about

possibility mean value of type-1 fuzzy sets which

introduce the lower and upper possibility mean value

for interval type-2 fuzzy sets. In this paper, the

comparative simulation results and between the

proposed pf the extension of Vectorial Centroid (Ku

Khalif and Gegov, 2015) and possibility mean value

that proposed by Gong et al. (2015) for interval

type-2 fuzzy sets is discussed. There are some

limitations exist in implementing Gong et al. (2015)

method for interval type-2 fuzzy sets, where in some

cases it will give illogical results that not consistent

with human intuition. This method also can cater all

possible cases of interval type-2 fuzzy sets properly

since some of the results are dispersed far away from

the closed interval bounded by the expectations

calculated from its upper and lower distribution

functions.

Due to growths in computational capability and

technology development, data are being generated

for understanding details real world problems in

health nowadays that associated with clinical tests,

diseases, disorder, genetic cases and so forth (Chen

et al., 2011). However, with the availability of large

datasets become the essential challenges of a new

methods of statistical analysis and modelling.

Logistic regression model is one of machine learning

technique that used in handling these problems with

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

high-dimensional data. The dataset that represents

binary dependent attribute where it uses logit

transform to predict probabilities directly. Logistic

regression is a model-based approach to mapping

observers’ distribution. When applied within

Bayesian setting, logistic regression provides a

useful platform for integrating expert knowledge, in

the form of a prior, with empirical data (Choy,

2013). Probability is complete with parametric

models that let us characterize random uncertainty

(Mendel and Wu, 2006).

Issues with respects to representation capability

of fuzzy sets in machine learning systems on

uncertainty become one of the important problems in

decision making environments. The main objective

of the present paper is to illustrate the extension of

Vectorial Centroid (Ku Khalif and Alex, 2015)

method for interval type-2 fuzzy sets that consider

the illustration of Bayesian algorithm about the

parameters of a logistic regression model. Aiming at

the problems pointed out above, new centroid

defuzzification for interval type-2 fuzzy sets is

proposed that easy to understand, more flexible and

more intelligent compared to existing methods. The

proposed method also considers the need of human

intuition and gives logical results while dealing with

machine learning systems. In this research study,

classification dataset with binary dependent attribute

is used. The observations in this dataset, we will

work on “BUPA liver-disorder” that were sampled

by BUPA Medical Research Ltd. There are 7

attributes that consist of six independent attributes

and one binary dependent attribute. The BUPA

liver-disorder dataset represents blood tests

indicating a property of liver disorders that may

increase from excessive alcohol consumption.

The remainder of this paper is organised as

follows: Section II introduces the concepts of type-2

fuzzy set, interval type-2 fuzzy set, centroid method

that proposed by Gong et al. (2015) and Bayesian

logistic regression. Section III views the proposed

new centroid method for interval type-2 fuzzy sets

using Vectorial Centroid method. Section IV

illustrates the implementation of proposed method

with Bayesian logistic regression in BUPA liver-

disorder and compares the results with Gong et al.

(2015) method. Section V summarises the main

results and draws conclusion.

2 PRELIMINARIES

In this section, we briefly review some concepts of

interval type-2 fuzzy sets (IT2 FSs), Bayesian

logistic regression and interval-value possibility

mean

2.1 Interval Type-2 Fuzzy Sets

Definition 1: A type-2 fuzzy set (T2 FS)

≈

in the

universe of discourse X represented by the type-2

membership function

. If all 1),( =

≈

, then

≈

is called an interval type-2 fuzzy sets (IT2 FSs). An

IT2 FS can be considered as a special case T2 FS,

denoted as follows (Deng, 2013):



∈∈

≈

XxJu

uxA ),/(1

(1)

where

[]

1,0⊆

J .

Definition 2: The upper and lower membership

function of an IT2 FS are type-1 fuzzy sets (T1 FSs)

membership functions, respectively. A trapezoidal

interval type-2 fuzzy sets can be represented by

,()),

(

(;,,,(()

(

14321

aAHAHaaaaAAA ==

≈

)))

(),

(;,,

21432

AHAHaaa where can be shown in

Figure 1 (Gong et al., 2015). The

and

are T1

FSs,

aaaaaaa

3214321

,,,,,,

and

are the

reference points of the IT2 FS

≈

, )

(

AH denote

the membership value of the element

)1( +

in the

upper trapezoidal membership function

21 ≤≤ j , )

(

AH denotes the membership value of

the element

)1( +

in the lower trapezoidal

membership function

, 21 ≤≤ j , and for

]1,0[)

(

∈

AH , ]1,0[)

(

∈

AH , ]1,0[)

(

∈

AH ,

]1,0[)

(

∈

and ni ≤≤1 ,

]1,0[)

(

∈

(Deng,

2013).

Definition 3: The arithmetic additional operation

between the trapezoidal IT2 FSs

,()),

(),

(;,,,(()

(

11121114131211111

LUUUUUULU

aAHAHaaaaAAA ==

≈

)))

(),

(;,

12111412

LLLL

AHAHaa and ,(()

(

21222

ULU

aAAA ==

≈

LLUUUULLLU

aaAHAHaaAHaaa

22212221242321242322

,()),

(),

(;,),

(;,,

)))

(

AH is defined as follows (Lee and Chen,

2008):

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets

)

()

(

2211

LULU

AAAAAA +=+

≈≈

;,,,((

2414231322122111

UUUUUUUU

aaaaaaaa ++++=

)),

((),

(min()),

((),

(min(

22122111

UUUU

AHAHAHAH

;,,,((

2414231322122111

LLLLLLLL

aaaaaaaa ++++=

)))

((),

(min()),

((),

(min(

22122111

LLLL

AHAHAHAH

(2)

Definition 4: The arithmetic substraction operation

between the trapezoidal IT2 FSs

,()),

(),

(;,,,(()

(

11121114131211111

LUUUUUULU

aAHAHaaaaAAA ==

≈

)))

(),

(;,

12111412

LLLL

AHAHaa and ,(()

(

21222

ULU

aAAA ==

≈

LLUUUULLLU

aaAHAHaaAHaaa

22212221242321242322

,()),

(),

(;,),

(;,,

)))

(

is defined as follows (Lee and Chen,

2008):

)

()

(

2211

LULU

AAAAAA −=−

≈≈

;,,,((

2414231322122111

UUUUUUUU

aaaaaaaa −−−−=

)),

((),

(min()),

((),

(min(

22122111

UUUU

AHAHAHAH

;,,,((

2414231322122111

LLLLLLLL

aaaaaaaa −−−−=

)))

((),

(min()),

((),

(min(

22122111

LLLL

AHAHAHAH

(3)

Definition 5: The arithmetic multiplication

operation between the trapezoidal IT2 FSs

,()),

(),

(;,,,(()

(

11121114131211111

LUUUUUULU

aAHAHaaaaAAA ==

≈

)))

(),

(;,

12111412

LLLL

AHAHaa and ,(()

(

21222

ULU

aAAA ==

≈

LLUUUULLLU

aaAHAHaaAHaaa

22212221242321242322

,()),

(),

(;,),

(;,,

)))

(

is defined as follows (Lee and Chen,

2008):

)

()

(

2211

LULU

AAAAAA ×=×

≈≈

;,,,((

2414231322122111

UUUUUUUU

aaaaaaaa ××××=

)),

((),

(min()),

((),

(min(

22122111

UUUU

AHAHAHAH

;,,,((

2414231322122111

LLLLLLLL

aaaaaaaa ××××=

)))

((),

(min()),

((),

(min(

22122111

LLLL

AHAHAHAH

(4)

Definition .6: The arithmetic operation between the

trapezoidal IT2 FSs

,,,(()

(

131211111

UUULU

aaaAAA ==

≈

)))

(),

(;,,()),

(),

(;

1211141211121114

LLLLLUUU

AHAHaaaAHAHa

and the crisp constant value k is defined as follows

(Lee and Chen, 2008):

))),

((),

(;,,,(

221114131211

LLLLLL

AHAHakakakak ××××

)),

((),

(;

((

221114131211

UUUUUU

AHAHa

××××=

≈

)))

((),

(;

(

221114131211

LLLLLL

AHAHa

××××

(5)

where

0>k .

Figure 1: The upper trapezoidal membership function

and lower trapezoidal membership function

IT2 FSs.

2.2 Bayesian Logistic Regression

The principal of Bayesian inference for logistic

regression analyses follows the typical pattern for

Bayesian analysis (Joseph, 2015):

1. Write down the likelihood function of the data

2. Form a prior distribution over all unidentified

parameters

3. Find posterior distribution using Bayes theorem

over all parameters

Likelihood function: the likelihood contribution from

the

i subject is binomial

)))(1()(

xxlikelihood

−

−=

ππ

(6)

where

)(

represents the probability of the event

for subject i, which has covariate vector

x and

specifies the liver-disorder

y , or liver-normal

y of the event for the subject. Logistic

regression is denoted as

ppi

βββ

+++

...

)(

(7)

So the likelihood from the

i subject is

)1(

...

...1

...

110

ippi

likelihood

−

+++













−













βββ

∏

−

+++

























−













ippi

likelihood

)1(

...1

...

...1

...

110

βββ

(8)

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

Prior distribution: in general, any prior distribution

can be used, depending on the available prior

information.

),(~

jjj

cNormal

σβ

(9)

The most common choice for c is zero, and

usually chosen to be large enough to be considered

as non-informative in the range from

10=

100=

Posterior distribution via Bayes theorem: the

posterior distribution is divided by multiplying the

prior distribution over all parameter by the full

likelihood function, so that

∏

−

+++

























−













ippi

Posterior

)1(

...1

...

...1

...

110

βββ



exp

































−

−×

πσ

(10)

The latter part of the above expression being

recognised as normal distribution for the

parameters. For liver-disorder classification

problem,

)1(

xyp

= , will be an estimate of the

probability that the pth document belongs to the

category. The decision of whether to assign the

category can be based on comparing the probability

estimate with a threshold or by computing which

decision gives optimal expected utility.

2.3 Interval-Valued Possibility Mean

Value

The concept of interval-valued possibility mean

value are divided into two parts which are lower and

upper possibility mean value. The lower

)(

≈

AM and

upper

)(

≈

AM possibility mean value for interval

type-2 fuzzy sets are denoted as follow (Gong et al.,

2015):















−













−

≈

aAM

)(

βββααα

(11)















−













−

≈

aAM

)(

βββααα

(12)

For crisp value, we can compute by using the

average of lower and upper possibility mean value

above that denoted as follows

)(

≈

(13)

In this paper, the numerical analysis for proposed

methodology is compared with interval-valued

possibility mean value that proposed by Gong et al.

(2015).

3 PROPOSED METHOD

As noted in the introduction, the useful of interval

type-2 fuzzy sets nowadays are widely applied in

many research areas in dealing with uncertainty in

data analysis which consistent with human intuition.

Most of researchers attempt to eliminate the need of

human intuition in data analysis processes. Human

intuition is strictly can’t be eliminated because it can

lead us towards uncertainty problems.

This study simplify the concept of attributes to

]1,0[∈

≈A

for fuzzy events. The values of attributes

correspond to interval type-2 fuzzy sets. This study

proposed a new centroid defuzzification

methodology for Bayesian logistic regression

algorithm. The methodology consist of two stages

here namely:

A. Stage one

The development of an extension of the Vectorial

Centroid defuzzification [29] for interval type-2

fuzzy sets.

B. Stage two

The implementation of Vectorial Centroid in

Bayesian logistic regression.

Full description for both stages are as follow:

A. Stage one

Let consider by

,,(()

(

aaAAA ==

≈

)))

(),

(;,,,()),

(

(;,

214321

143

AHAHaaaaAHAHaa

as the interval type-2 fuzzy sets. The complete

method process of Vectorial Centroid is signified as

Step 1: Find the centroids of the three parts of

and

in interval type-2 fuzzy set representation as

shown in Figure 2.













++++= )(

(

)

(

),(

2121

LULLUU

hhaaaayx

αα

(14)













++++= )(

),(

3232

LULLUU

hhaaaayx

ββ

(15)

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets

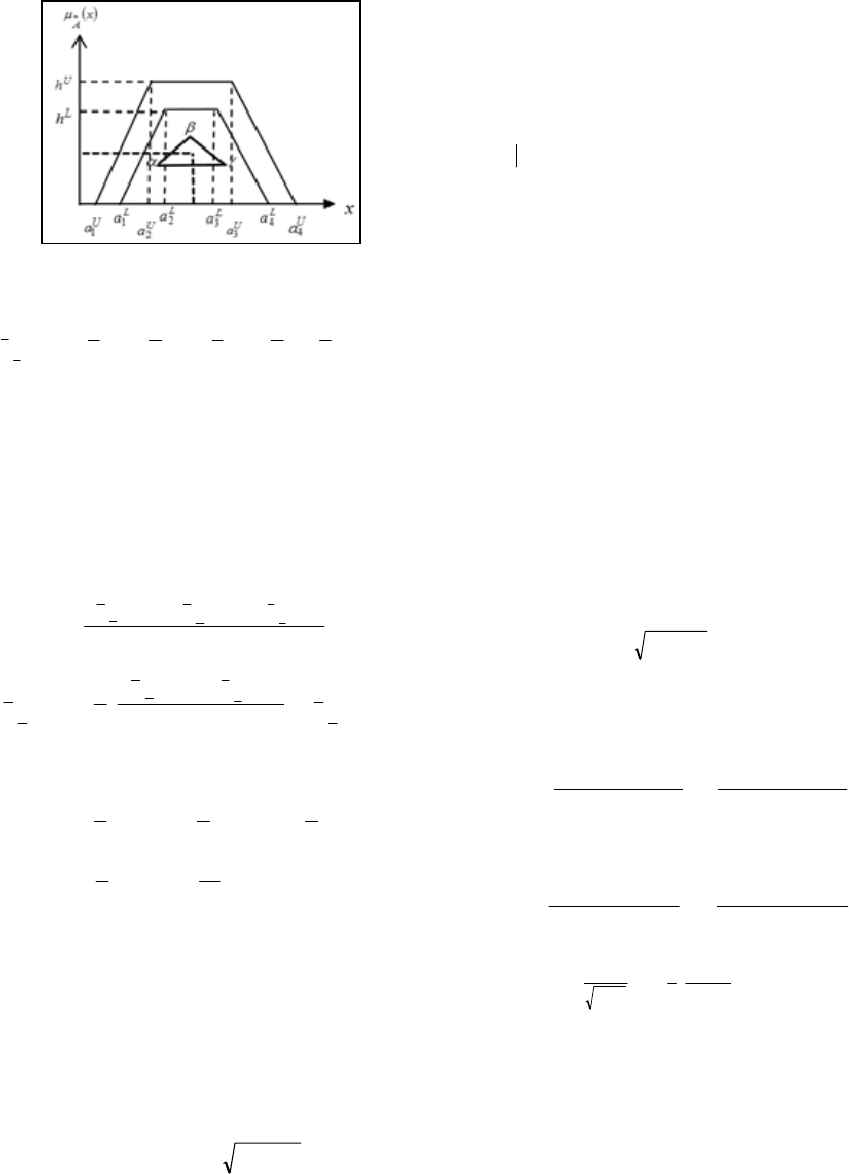
Figure. 2: Vectorial Centroid plane representation.













++++= )(

(

)

(

),(

4343

LULLUU

hhaaaayx

γγ

(16)



ep 2: Connect all vertices centroids points of

and

each other, where it will create another

triangular plane inside of trapezoid plane.

Step 3: The centroid index of Vectorial Centroid of

)

( yx

with vertices

and

can be calculated







≈

),(),(),(

)

(

,,,

yxyxyx

yxVC

γγββαα

γβα































−

+ ),(

),(),(

),(

yxyx

ββ

γγαα

ββ

γα

(17)

Vectorial Centroid can be summarised as













++++++=

≈

)(

)

(

332211

LULULU

aaaaaayxVC













+ )(

,)(

LULU

hhaa (18)

where

: the centroid coordinate of first triangle plane

: the centroid coordinate of rectangle plane

: the centroid coordinate of second triangle plane

)

( yx : the centroid coordinate of fuzzy number

≈

Centroid index of Vectorial Centroid can be

generated using Euclidean distance by Cheng

(1998):

)( yxAR +=

≈

(19)

B. Stage two

Integrating fuzzy sets with Bayesian logistic

regression in fuzzy states of nature, where if there is

fuzzy dataset, defuzzification process is needed in

converting into crisp values where at the same time

the fuzzy nature is not lost. Reinterpretation of

degree

]1,0[∈

≈

using Vectorial Centroid to the

)1(

XyP

is developed as follows:

Step 1: Lift the reintergration of the fuzzy values

membership function using trapezoidal interval type-

2 fuzzy sets. Vectorial Centroid formulation are

applied for trapezoidal interval type-2 fuzzy set rule

formula. The

≈

represents as

,()),

(),

(;,,,(()

(

11121114131211111

LUUUUUULU

aAHAHaaaaAAA ==

≈

)))

(),

(;,

12111412

LLLL

AHAHaa in calculation to avoid

cluttering. Suppose that

are fuzzy events for

attribute alkaline phosphatase, aspartate

aminotransferase, gamma-glutamyl transpeptidase

and alamine aminotransferase in BUPA liver-

disorder dataset.

Step 2: The centroid index of Vectorial

Centroid,

)(

≈

is inserted into Bayesian logistic

regression rule as

)(

≈≈

=+= AyxAR

The computational process of likelihood and

posterior distribution of fuzzy Bayesian logistic

regression using Vectorial Centroid are denoted as

∏

−

+++

























−













≈≈

ippi

likelihood

)1(

)(...)(

110

μβμββ

(20)

∏

−

+++

























−













≈≈

ippi

Posterior

)1(

)(...)(

110

μβμββ



exp

































−

−×

πσ

(21)

4 EXPERIMENTAL SETTINGS

In this section, we describe the required parameters

to conduct the experiments. The experiment is

conducted using 10-fold cross validation on BUPA

liver-disorder dataset from UCI machine learning

repository (Forsyth, 2015) is used where donated by

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

BUPA Medical Research Ltd. This liver-disorder

classification dataset has 345 examples, 7 attributes

and binary classes for dependent attribute. The first

5 attributes are measurements taken by blood tests

that are thought to be sensitive to liver-disorders and

might arise from excessive alcohol consumption.

The sixth attribute is a sort of selector attribute

where the subjects are single male individuals. The

seventh attribute shows a selector on the dataset

which being used to split into two categories that

indicating the class identity. The attributes include:

a. Mean corpuscular volume,

b. Alkaline phosphatase,

c. Aspartate aminotransferase,

d. Gamma-glutamyl transpeptidase,

e. Alamine aminotransferase,

f. Number if half-pint equivalents of

alcoholic beverage drunk per day, and

g. Output attributes either liver disorder or

liver normal

Among all the people, there are 145 belonging to the

liver-disorder group and 200 belonging to the liver-

normal group. These attributes are selected with the

aid of experts. The original dataset are fuzzified

randomly in interval type-2 fuzzy sets form in

operating centroid methods. Below depicts the

example of interval type-2 fuzzy sets are used in this

research study:

Example 1: If the trapezoidal interval type-2 fuzzy

set

20.51;1),.68,18.06,((15.35,16)

( ==

≈

AAA

19;0.9))(16,17,18,

, then the centre points are

computed using proposed (Vectorial Centroid) and

established method (Interval-valued possibility mean

value) formulation respectively as follows:

Vectorial Centroid:

3678.17)( =xVC

and

58056.0)( =yVC

Index Vectorial Centroid,

3775.17)( =

≈

RVC

Interval-Valued Possibility Mean Value:

[]

8633.16,8683.14)(),()( =













≈

∗

≈

∗

≈

AMAMAM

Crisp possibility mean value,

8658.15)( =

≈

5 SIMULATION RESULTS

This section illustrates the validation process that are

divided into two parts which are theoretically and

empirically. Therefore, the theoretical of Vectorial

Centroid validation process are as follow:

A. Stage one

The relevant properties considered for justifying the

applicability of centroid for interval type-2 fuzzy

sets, where they depend on the practicality within

the area of research however, they are not

considered as complete. Therefore, without loss of

generality, the relevant properties of the centroid are

as follow:

Let

≈

and

≈

are be trapezoidal and triangular

interval type-2 fuzzy sets respectively, while

)

( yxMC

≈

and

)

( yxMC

≈

be centroid points for

≈

and

≈

respectively. Centroid index of Vectorial

Centroid, (R) shows the crisp value of centroid point

that is denoted as

)( yxAR +=

≈

Property 1: If

≈

and

≈

are embedded and

symmetry, then

)()(

≈≈

> BRAR

Proof:

Since

≈

and

≈

are embedded and symmetry, hence

from equation (19) we have

2222

~~~~

≈≈≈≈

+>+

BBAA

yxyx

Therefore,

)()(

≈≈

> BRAR

Property 2: If

≈

and

≈

are embedded with

≈≈

hhhh ),(),(

, then

)

()

( BRAR >

Proof:

Since

≈

and

≈

are embedded and

with

≈≈

hhhh ),(),(

, hence we know that

> .

Then, from equation (19) we

have

2222

~~~~

≈≈≈≈

+>+

BBAA

yxyx

. Therefore,

)()(

≈≈

> BRAR

Property 3: If

≈

is singleton fuzzy number, then

)(

≈≈

≈

yxAR

Proof:

For any crisp (real) interval type-2 fuzzy set, we

know that

≈

========

LLLLUUUU

xaaaaaaaa

43214321

which are equivalent to equation (18).

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets

Therefore,

)(

≈≈

≈

yxAR

Property 4: If

≈

is any symmetrical or asymmetrical

interval type-2 fuzzy number, then

aARa

)( <<

≈

Proof:

Since any symmetrical or asymmetrical interval

type-2 fuzzy set has

UUUU

aaaa

4321

≤≤≤

, hence

ayxMCa

)

( <<

≈

. Therefore,

aARa

)( <<

≈

B Stage two

In this stage, the empirical validation is implemented

where the BUPA liver-disorder data set is used in

conducting Bayesian Logistic Regression

Note that this study is considered all type of possible

interval type-2 fuzzy sets for attributes randomly as

figures follow:

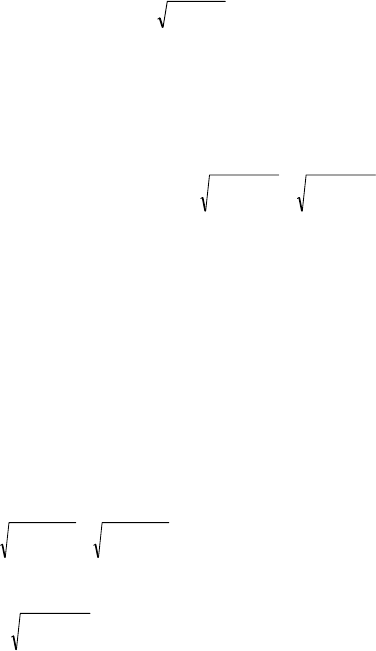
Figure 3: Trapezoidal Non-Normal Symmetry.

Figure 4: Trapezoidal Normal Symmetry.

Figure 5: Trapezoidal Non-Normal Asymmetry.

Fig. 6: Trapezoidal Normal Asymmetry.

Figure 7: Triangular Non-Normal Symmetry.

Figure 8: Triangular Normal Symmetry.

Figure 9: Triangular Non-Normal Asymmetry.

Table I presents a comparative results between

classical Bayesian logistic regression (BLR-Classic),

Bayesian logistic regression using possibility mean

value (Gong et al., 2015) method (BLR-PMV), and

Bayesian logistic regression using proposed Vectorial

Centroid (BLR-VC). The comparison results are

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

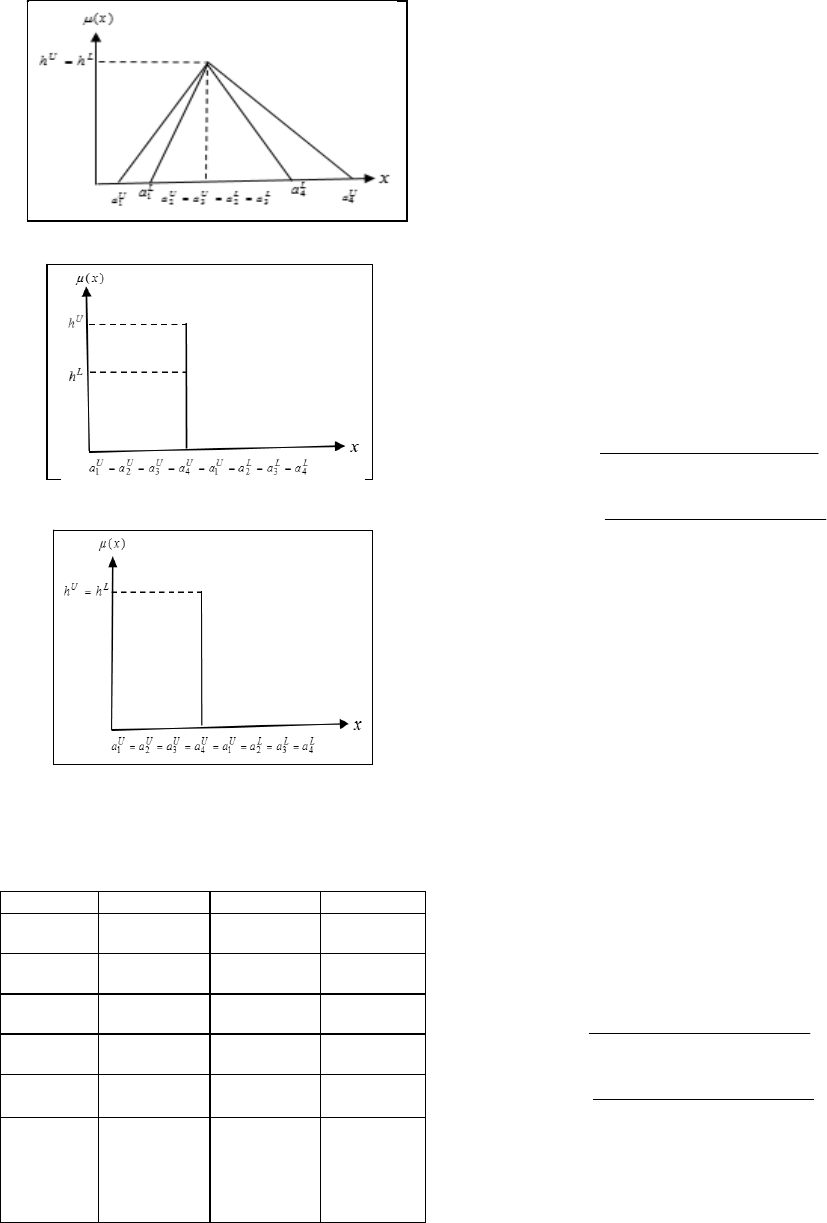
Figure 10: Triangular Normal Asymmetry.

Figure 11: Singleton Non-Normal.

Figure 12: Singleton Normal.

Table 1: Accuracy, precision, sensitivity, specificity, kappa

statistic and errors results.

Method BLR-Classic BLR-PMV BLR-VC

Accuracy

67.2464% 58.5507% 68.1159%

Precision

17.67% 1.4% 30.34%

Sensitivity

82% 66.67% 83.02%

Specificity

64.75% 58.41% 65.41%

Kappa

Statistic

0.2613 0.0203 0.2832

Errors:

MAE

RMSE

RAE

RRSE

0.3275

0.5723

67.2025%

115.9404%

0.4145

0.6438

85.0438%

130.4259%

0.3188

0.5647

65.4183%

114.391%

Centroid (BLR-VC). The comparison results are

based on accuracy precision, sensitivity, specificity,

kappa statistic, and some error terms which are Mean

Absolute Error (MAE), Root Mean Square Error

(RMSE), Relative Absolute Error (RAE) and Root

Relative Square Error (RRSE).

The accuracy and precision of a measurement

system plays significant role in quantifying the actual

measure value. It is commonly used as metric for

evaluation of machine learning systems. The

precision is dependent of accuracy where the model

can be very precise but inaccurate. The higher the

value of accuracy and precision, the better

classification prediction is made. In this research

study, Table 1 shows the classification accuracy

results that show the correctness of a model classifies

the dataset in each class. Below show the formulation

of accuracy and precision:

NegativePositive

iveTotalNegativeTotalPosit

Accuracy

: (22)

iveFalseNegativeTotalPosit

iveTotalPosit

ecision

:Pr (23)

The classification accuracy results of BLR-Classic,

BLR-PMV and BLR-VC are 67.2464%, 58.5508%

and 68.1159% respectively. It shows that the

proposed methodology is significantly more accurate

compared to others. The highest precision in this case

study is BLR-VC with 30.34%, followed by BLR-

Classic with 17.67% and BLR-PMV with 1.4%.

Precision discusses the closeness of two or more

measurements to each other.

The sensitivity test refers to the ability of the test

to correctly identify those observers with positive

predictive value. A high sensitivity is clearly

imperative where the test is used to identify the

correct class. But, specificity test is inversely

proportional to sensitivity where it has the ability of

the test to correctly identify those observers with

negative predictive value (Lalkhen and McCluskey,

2015). Below are formulation to calculate sensitivity

and specificity:

iveFalseNegativeTotalPosit

iveTotalPosit

ySensitivit

: (24)

iveTotalNegativeFalsePosit

iveTotalNegat

ySpecificit

: (25)

The proposed method, BLR-VC produces the highest

sensitivity and specificity value with 83.02% and

65.41% respectively. The results for BLR-PMV

shows the lowest results for sensitivity and

specificity with 66.67% and 58.41% respectively. It

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets

depicts that the goodness of prediction of both tests

for BLR-PMV is lesser than BLR-Classic and BLR-

VC.

Kappa statistic technique is used to measure the

agreement of two classifiers and estimate the

probability of two classifiers agree simply by chance

(Jeong et al., 2010). Known as chance-corrected

measure of agreement between classification and the

true classes, it is an evaluation metric which is based

on the difference between the actual agreement in the

error matrix and the chance agreement. The values

for Kappa range from 0 to 1 and the higher the value

of kappa statistic, the stronger the strength of

agreement between two classifiers by chance.

kKappaStat

−

(26)

where

p is relative observed agreement among

raters, and

is the hypothetical probability of

chance agreement.

Referring Table 1, BLR-VC shows the highest

value of kappa statistic with 0.2832 followed by

BLR-Classic and BLR-PMV with 0.2613 and 0.0203

respectively.

The last part in Table I depicts the errors for the

experiment carried out. The errors are computed by

using Mean Absolute Error (MAE), Root Mean

Square Error (RMSE), Relative Absolute Error

(RAE) and Root Relative Square Error (RRSE). All

the statistic errors compare true values to theirs

estimates, but do it in a slightly different way. Below

depict the formulation in calculating MAE, RMSE,

RAE and RRSE:



−=

MAE

θθ

(27)



−=

RMSE

)

(

θθ

(28)



−

RAE

θθ

(29)



−

RRSE

)(

)

(

θθ

(30)

These error terms show how disperse away the

estimated values from the true value of

. MAE and

RMSE calculate the average difference between

those two values. In RAE and RRSE, we divide those

differences by the variation of

where they have a

scale from 0 to 1, then we would multiply those

value by 100 to get the similarity in 0-100 scale. In

this case study, the proposed methodology, BLR-MC

performs better results in error terms where all of

these errors are less than BLR-Classic and BLR-

PMV.

6 CONCLUSION

This study has brought out an extension based

Vectorial Centroid (Ku Khalif and Gegov, 2015) for

interval type-2 fuzzy sets with Bayesian logistic

regression. Bayesian logistic regression algorithm

that takes into account the need of fuzzy events in

attributes. This work suggests Vectorial Centroid

defuzzification on interval type-2 fuzzy sets method

for Bayesian logistic regression which consist of two

stages which are: The development of Vectorial

Centroid defuzzification method for interval type-2

fuzzy sets: and the implementation of Vectorial

Centroid in Bayesian logistic regression. For the first

stage, the development of new centroid method can

cater all the possible cases of interval type-2 fuzzy

sets precisely that matching for human intuition. The

implementation in Bayesian logistic regression using

proposed methodology on stage two is easily

capable constructed and handled in data analysis

when dealing with fuzzy data sets.

Several limitations may exist in this research

study. First, the proposed classification model for

interval type-2 fuzzy numbers was developed and

tested on BUPA liver-disorder dataset from WEKA

software. The useful of interval type-2 fuzzy sets are

randomly applied. Second, the scope of this research

study is focused to be automated diagnosis liver-

disorder. Still, more experimental work should be

enthusiastic to obtain a medical classification model

with a better ability of generalization under fuzzy

environment. The proposed Vectorial Centroid only

applied in one machine learning which is Bayesian

logistic regression. It should be applied and

compared with more machine learning systems in

the future work that would make research much

more convincing.

Furthermore, this study can be valuable

alternatively in the set of existing Bayesian logistic

regression algorithms for numerous problems in

machine learning such as inference, classification,

FCTA 2015 - 7th International Conference on Fuzzy Computation Theory and Applications

clustering, regression and so forth. There are four

relevant properties for centroid development are

constructed and well proved in theoretical

validation, where corresponding with all possible

interval type-2 fuzzy sets representation. Several

tests for validation have been done and the results

have been studied in-depth using BUPA liver-

disorder classification dataset from UCI machine

learning repository. The validation results show the

proposed research study more effective in dealing

with fuzzy events empirically. Finally, it can be

concluded that the main focus of this research study

can be proceeded in order to make some

contributions by considering real case study drawn

for diverse fields crossing ecology, health, genetics,

finance and so forth.

REFERENCES

Carlsson, C., Fuller, R. 2001. On possibilistic mean value

and variance of fuzzy numbers, Fuzzy Sets and

Systems, vol. 122.

Chen, C.C.M., Schwender, H., Keith, J., Nunkesser, R.,

Mengersen, K., Macrossan, P. 2011. Method of

identifying SNP interactions: A review on variations of

logic regression, random forest and Bayesian logistic

regression, IEEE/ ACM Transactions on

Computational Biology and Bioinformatics, vol. 8. a

Cheng, C.H. 1998. A new approach for ranking fuzzy

numbers by distance method, Fuzzy Sets and Systems,

vol. 95.

Choy, S.L. 2013. Priors: Silent or active partners of

Bayesian inference?, Case Studies in Bayesian

Statistical Modelling and Analysis, John Wiley &

Sons Ltd, Sussex.

Deng, H. 2013. Comparing and ranking fuzzy numbers

using ideal solutions, Applied Mathematics

Modelling, vol. 38.

Forsyth, R.S. 2015. Liver disorder data set, UCI Machine

Learning Repository: Internet Source:

https://archive.ics.uci.edu/ml/datasets/Liver+Disorders

[Feb. 1, 2015].

Gong, Y., Hu, N., Zhang, J., Liu. G., Deng. J. 2015. Multi-

attribute group decision making method based on

geometric Bonferroni mean operator of trapezoidal

interval type-2 fuzzy numbers, Computer and

Industrial Engineering, vol. 81.

Hullermeier, E. 2011. Fuzzy sets in machine learning and

data mining, Applied Soft Computing, vol. 11.

Jeong, D., Kang, D., Won, S. 2010. Feature selection for

steel defects classification, International Conference

on Control, Automation and Systems.

Joseph. 2015. Bayesian inference for logistic regression

parameters. Internet Source: http://www.medicine.

mcgill.ca/epidemiology/joseph/courses/EPIB-621/

bayeslogit.pdf [March, 15, 2015].

Karnik, N.N., Mendel, J.M. 2001. Centroid of type-2 fuzzy

set, Information Sciences, vol. 132.

Klir, G., Yuan, B. 1995. Fuzzy sets and fuzzy logic:

Theory and applications, Prentice Hall, Upper Saddle

River.

Ku Khalif, K.M.N., Gegov, A. 2015. Generalised fuzzy

Bayesian network with adaptive Vectorial Centroid,

World Congress of the International Fuzzy

Systems Association (IFSA) and 9

Conference of

European Society for Fuzzy Logic and Technology

(EUSFLAT).

Lalkhen, A.G., McCluskey, A. 2015. Clinical test

sensitivity and specificity, Internet Source:

http://ceaccp.oxfordjournals.org/content/8/6/221.full

[March, 16, 2015].

Lee, L.W., Chen, S.M. 2008. Fuzzy multiple attributes

group decision-making based on the extension of

TOPSIS method and interval type-2 fuzzy sets, 7

IEEE International Conference on Machine Learning

and Cybernatics.

Liu. F. 2008. An efficient centroid type-reduction strategy

for general type-2 fuzzy logic system, Information

Sciences, vol. 178.

Mendel, J.M. 2001. Uncertain rule-based fuzzy logic

systems: Introduction and new directions, Prentice-

Hall, Upper Saddle River, New Jersey.

Mendel, J.M., John, R.I., Liu, F.L. 2006. Interval type-2

fuzzy logical systems made simple, IEEE Transactions

on Fuzzy Systems, vol. 14.

Mendel, J.M., Wu, H.W. 2006. Type-2 fuzzistic for

symmetric interval type-2 fuzzy sets: Part 1, forward

problems, IEEE Transactions on Fuzzy Systems, vol.

14.

Mogharreban, N., Dilalla, L.F. 2006. Comparison of

defuzzification techniques for analysis of non-interval

data, Fuzzy Information Processing Society.

Tang, Y., Pan, H., Xu, Y. 2002. Fuzzy naïve Bayes

classifier based on fuzzy clustering, Systems, Man and

Cybernatics, IEEE International Conference, vol. 5.

Wagner, C., Hagras, H. 2010. Uncertainty and type-2

fuzzy sets systems, IEEE UK Workshop on

Computational Intelligent (UKCI).

Wallsten, T.S., Budescu, D.V. 1995. A review of human

linguistic probability processing general principles

and empirical evidences, The Knowledge Engineering

Review, vol.10 (a).

Yager, R.R., Filev, D.P. 1994. Essential of fuzzy modelling

and control, Wiley, New York.

Zadeh, L.A. 1965. Fuzzy sets, Information and Control,

vol. 8.

Zadeh, L.A., 1975. The concept of a linguistic variable

and its application to approximate reasoning,

Information Sciences, vol. 8.

Zimmermann, H.J. 2000. An application – oriented view

of modelling uncertainty, European Journal of

Operational Research, vol 122.

Bayesian Logistic Regression using Vectorial Centroid for Interval Type-2 Fuzzy Sets