
Bayesian Sample Size Optimization Method for Integrated Test
Design of Missile Hit Accuracy
Guangling Dong
1
, Chi He
2
, Zhenguo Dai
3
, Yanchang Huang
3
and Xiaochu Hang
3
1
School of Astronautics, Harbin Institute of Technology, 92 Xidazhijie Street, Harbin, China
2
School of Mechatronic Engineering, CUST, 7089 Weixing Road, Changchun, China
3
Department of Test Technology, Baicheng Ordnance Test Center of China, Mailbox 108, Baicheng, China
Keywords: Missile Hit Accuracy, Integrated Test Design, Bayesian Sample Size Determination, Power Prior, Design
Prior.
Abstract: Sample size determination (SSD) for integrated test of missile hit accuracy is addressed in this paper.
Bayesian approach to SSD gives test designer the possibility of taking into account of prior information and
uncertainty on unknown parameters of interest. This fact offers the advantage of removing or mitigating
typical drawbacks of classical methods, which might lead to serious miscalculation of the sample size.
However, standard power prior based Bayesian SSD method cannot cope with integrated SSD for both
simulation test and field test, as large numbers of simulation samples would cause contradiction between
design prior and average posterior variance criterion (APVC). In allusion to this problem, we propose a test
design effect equivalent method for equivalent sample size (ESS) calculation, which combined simulation
credibility, sample size, and power prior exponent to get a rational design prior for subsequent field test.
Average posterior variance (APV) of interested parameters is deduced by simulation credibility, sample
sizes of two kinds of test, and prior distribution parameters. Thus, we get optimal design equations of
integrated test scheme under both test cost constraints and required posterior precision constraint, whose
effectiveness are illustrated with two examples.
1 INTRODUCTION
Hit accuracy is a key technical performance index in
missile weapon system, which is traditionally
testified through live field firing test. As its
extremely high expenditure in field test, we can only
get very limited test samples as a basis for type
approval to reach a low precision assessment result.
Thus, in order to solve this problem, integrated test
and evaluation with combined use of simulation test
and field test was put forward in 1990s (Kraft 1995;
Kushman and Briski 1992), and by now, it has
become the development direction of test and
evaluation (Claxton et al., 2012; Schwartz, 2010;
Waters, 2004). In the design stage of integrated test,
sample size allocation (SSA) for simulation test and
field test is a vital problem. Standard frequentist
sample size formulae generally determine a specific
sample size through precision requirement of
parameter estimation (Adcock, 1997) or statistical
power analysis of Hypnosis test (Murphy et al.,
2009), as used in design of integrated test, SSA ratio
become a problem, and also the equal treatment of
simulation test sample and field test sample is
widely questioned.
Generally, simulation test samples are strongly
correlated with field test samples, but they don’t
necessarily take on the same distribution parameters.
Verification validation and accreditation (VV&A) of
simulation system (Balci 1997, 2013; Rebba et al.,
2006) are made to get some indexes (such as
simulation credibility) for description of this
difference. Bayesian sample size determination
(SSD) (Clarke and Yuan, 2006; De Santis, 2007;
Joseph and Belisle, 1997; Nassar et al., 2011) makes
use of prior information to get the minimal sample
size through pre-posterior estimated performance
criteria of parameter of interest. While it is used in
SSD of integrated test, determining a proper weight
for prior information (De Santis, 2007) is a problem.
Also, the obtained power prior (Ibrahim and Chen,
2000) for design from large size of prior samples is
often narrow enough to estimate the unknown
parameter of interest, which seems no need for field
244
Dong G., He C., Dai Z., Huang Y. and Hang X..
Bayesian Sample Size Optimization Method for Integrated Test Design of Missile Hit Accuracy.
DOI: 10.5220/0005510902440253
In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),
pages 244-253
ISBN: 978-989-758-120-5
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

test samples. But, this totally inference of interested
parameter by simulation test samples is under
suspicion, and takes on great risk due to sometimes
low credible simulation test samples.
A proper design prior is the basis for Bayesian
SSD of integrated test, which is the key content of
our research. The rest of this paper is organized as
follows: Section 2 introduce the common used SSD
methods of both frequentist and Bayesian, as well as
the definitions of analysis prior and design prior
used in Bayesian SSD. Section 3 analyses the
problem of determining exponential factor in getting
design prior with power prior, and propose the
design effect of test to calculate the equivalent
sample size (ESS) of simulation test, which provide
the key content of our proposed method for getting a
rational design prior. Section 4 deals with optimal
SSA for simulation test and field test, which takes
average posterior variance of Bayesian estimation of
hit accuracy as output, and gets two optimization
equations under cost constraints and required
posterior precision constraint. Section 5 illustrates
the proposed methods with two examples, and
proves their effectiveness in practical application. In
section 6, the features of our proposed Bayesian
SSD for design of integrated test are summarized.
2 PRELIMINARIES
2.1 Classical Sample Size
Determination
Classical sample size determination method is
generally related to interval estimation and
hypothesis testing. Estimation of mean value μ for
normal distribution with known variance is the
simplest condition in SSD, many literatures (Adcock,
1997; Desu and Raghavarao, 1990) have made in-
depth study on this problem. Suppose we have a
given estimation error d and confidence level 1-α,
estimation of μ can be realized by sample mean, thus
the SSD formula is
Pr 1xd
(1)
As
() (0,1)nx N
, it follows that
inequality (1) is satisfied if sample size n satisfies
22 2
/2
nZd
(2)
Statistical power analysis of hypothesis testing
extends the rule at inequality(2). Suppose we have a
hypothesis of the form
00110
:;:HH
Significance level α of above hypothesis testing
means we reject H
0
while
02
x
Zn
. If
the desired power of the alternative when
10
d
is 1-β, where d is specified, then the
required sample size n is the solution of the
following equation
021
Pr 1xZn
Define
0
()Znx
, this could be expressed
as
2
Pr 1Znd Z
(3)
Equation (3) has a unique solution. Desu and
Raghavarao (1990) have made detail deduction and
gave out its approximate solution
*2 22
2
()nZZd
(4)
Equation (4) is valid as long as α is not too large,
and it reduces to inequality (2) when the desired
power is 0.5. While the variance σ
2
is unknown,
similar formulae can be gotten, for further detail, see
(Desu and Raghavarao, 1990) and reference therein.
Samples from simulation test and field test play
different roles in performance assessment, so their
sample size ratio and weights cannot be determined
arbitrarily. In this way, classical SSD method cannot
cope with situations in integrated test. As a result,
Bayesian SSD method become the inevitable choice
in design of integrated missile hit accuracy test.
2.2 Bayesian Sample Size
Determination
The key difference in SSD between Bayesian
method and classical method is the use of prior
information. Suppose that we are interested in
choosing the size n of a random sample X
n
=(X
1
, …,
X
n
), whose joint density function f
n
(|θ) depends on
the unknown parameter vector θ of interest. With
Bayesian approach, given sample data
1
,,
nn
x
x x
, the likelihood function
;|
nnn
Lx fx
, and the prior distribution π()
for parameter of interest, we get inference of θ based
on elaborations of the posterior distribution:
()()
()
()()d
nn
n
nn
f
f
x
x
x
BayesianSampleSizeOptimizationMethodforIntegratedTestDesignofMissileHitAccuracy
245

Let T(x
n
) denote a generic function of the
posterior distribution of θ, which can be controlled
by designed test sample size. For instance, T(x
n
)
could be either the posterior variance, or the width
of the highest posterior density (HPD) set or the
posterior probability of a certain hypothesis. Before
we get actual sample data x
n
, T(X
n
) is a random
variable. The idea of Bayesian SSD is to select n so
that the observed value T(x
n
) is likely to provide
accurate information on θ. Pre-computations for
SSD are made with the following marginal density
function of sample data
(;) ( )()d
nn nn
mx fx
Above equation shows a mixture of the sampling
distribution and the prior distribution of θ. Most
Bayesian SSD criteria select the minimal n so that,
for chosen values ε>0 and
(0,1)
, one of the two
following statements is satisfied:
E( )
n
T
X
(5)
or
Pr ( )
n
TA
X
(6)
Where, E[
] denotes the expected value computed
with respect to marginal density function m
n
. Pr[]
express the probability measure corresponding to m
n
.
A is a subset of the value space that the random
variable T(X
n
) can assume. Thus, SSD and the
subsequent parameter inference is a two-step process:
first select n* by a pre-posterior calculation; and
then use
*
()
n
x
to obtain T(x
n*
).
There are three common used Bayesian SSD
criteria for estimation, where criteria (b) and (c) are
interval type methods based on the idea of
controlling the random length of credible sets for
probability distribution, refer to (De Santis, 2007)
for further detail.
(a) Average posterior variance criterion (APVC):
for a given ε>0, APVC select the minimal sample
size n such that
Evar( )
n
X
(7)
Where, var(θ|X
n
) is the posterior variance of
interested unknown parameter θ, and
()var( )
nn
T
xx
, This criterion controls the
dispersion of the posterior distribution. Of course,
different dispersion measures can be used to derive
alternative criteria.
(b) Average length criterion (ALC): for a given
l>0, ALC looks for the minimal n to meet the
inequality
()
n
EL l
X
(8)
Where, for a fixed
(0,1)
, .L
α
(X
n
) is the random
length for the (1-α) level posterior set of θ. In this
case, T(x
n
) = L
α
(x
n
). This criterion was proposed by
Joseph (1995) (Joseph et al., 1995), aiming at
controlling the average length of the HPD set, but
not its variability.
(c) Length probability criterion (LPC): for given
l>0 and
(0,1)
, LPC choose the smallest n to
meet the inequality
Pr ( )
n
Ll
X
(9)
Just as for the ALC, T(x
n
)= L
α
(x
n
) and the LPC can
be written in the general form (6) with A = (l , U),
where U denotes the upper bound for the length of
the credible interval. Joseph and Belisle (1997)
derived the LPC as a special case of the worst
outcome criterion (WOC). Refer to (Di Bacco et al.,
2003; Joseph et al., 1995) for further details.
SSD criteria for model selection and hypothesis
testing are also available in many literatures such as
(De Santis, 2004; Reyes and Ghosh, 2013; Wang
and Gelfand, 2002; Weiss, 1997). As they are not
suitable for sample size determination of integrated
test design, we will not make detailed instruction
here. For further information, refer to literatures
above.
2.3 Two Priors in Bayesian SSD
Two priors approach to SSD, namely analysis prior
and design prior, has been already proposed, for
instance, by Spiegelhalter and Freedman (1986) and
by Joseph et al. (1997). By now, this approach has
gotten wide spread usage in many fields. Generally,
analysis prior formalizes the pre-test knowledge that
we want to take into account, together with test
samples, in the final analysis. While design prior
describes a scenario which is not necessarily
coincident with that of analysis prior, under which
we want to choose the sample size. Thus, design
prior serves to obtain a marginal distribution m
n
that
incorporates uncertainty on a guessed distribution
for θ. Refer to (De Santis, 2007) for a thorough
discussion on this question.
In general, analysis prior can be improper (such
as some non-informative priors) as long as the
resulting posterior is proper. While the design prior
is used for calculating marginal distribution m
n
, if it
is improper, the resulting marginal distribution may
not even exist and the integral that defines m
n
being
divergent. So, proper design prior should be chosen
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
246

in Bayesian SSD of integrated test. In order to use
historical data for Bayesian SSD, De Santis (2007)
went into this problem and gave out a method for
getting design prior of location parameter.
According to his analysis results, non-informative
prior can be used as analysis prior for simulation test
samples, and the obtained posterior distribution is
proper, which constitutes a suitable prior for
subsequent SSD of field test.
However, as simulation test samples are not
totally credible, the obtained posterior cannot be
used directly as design prior of field test. Power
prior (De Santis, 2007; Fryback et al., 2001;
Greenhouse and Waserman, 1995) has been taken as
a method for incorporating historical information in
a design prior and also for deciding the weight that
such information has in the SSD process. Therefore,
rational design prior for SSD of field test can be
obtained based on simulation test samples and a
proper use of power prior, which will be discussed
in detail in the next section.
3 EQUIVALENT SAMPLE SIZE
FOR DESIGN PRIOR
In this section we penetrate into the design prior for
Bayesian SSD of field test. The problem and
contradiction of using standard power prior from
simulation test samples as the design prior of
Bayesian SSD in integrated test will be analysed,
which lead to our proposed design effect of test for
calculating equivalent sample size (ESS) of
simulation test. Thus, we get the ESS based design
prior for Bayesian SSD.
3.1 Power Prior for Design
Power prior is often used in obtaining design prior of
Bayesian SSD, which realizes the weighting fusion
of prior information. Ibrahim and Chen (Ibrahim et
al., 2003; Ibrahim and Chen, 2000) proposed the
application of power prior in information fusion and
regression modelling, and analysed its superiority
therein. Suppose
0
n
z
is prior data with size n
0
used
for providing design prior of field test;
0
(; )
n
L
z
is
likelihood function of θ in
0
n
z
, here homogeneity of
prior samples and subsequent field test samples is an
implicit assumption; π
0
(θ) is non-informative prior.
Consider posterior distribution
0
P
0
(| , )
n
a
z is
obtained through multiplication of prior distribution
π
0
() and likelihood function
0
(; )
n
L
z
, suitably
scaled by an exponential factor a
0
:
0
00
P
00
0
(| , ) ()(; )
(0,1)
a
nn
aL
a
zz
(10)
If π
0
is proper,
0
P
0
(| , )
n
a
z is also proper;
otherwise,
0
n
z
should make
0
P
0
(| , )
n
a
z a proper
distribution function. Exponent a
0
measures the
importance of prior data in
0
P
0
(| , )
n
a
z . As a
0
→1,
we get standard posterior distribution of θ with
0
n
z
;
while as a
0
→0,
0
P
0
(| , )
n
a
z tends to initial non-
informative prior π
0
. Thus, exponent a
0
determines
the weight of
0
n
z
in posterior distribution. This
shows we can choose different a
0
for alternative
weights on prior information. Spiegelhalter et al.
(2004) have gone through this question. Following
the definition of power prior, we can get it with a
mixture of expression (10) and distribution of a
0
.
The effect of mixing is to obtain a prior for θ that
has a much heavier tails than those which are
obtained with fixed a
0
. Obviously, exponent a
0
plays
an important role in power prior calculation.
As to Bayesian SSD of integrated test, field test
samples X
n
is still to be observed, we assume π
0
is
non-informative prior, and
0
P
0
(| , )
n
a
z as the
design prior obtained from
0
n
z
, a proper marginal
distribution of the data X
n
can be gotten from
00
P
00
(|,) (|)(|,)d
nnn nn n
maf a
xz x z
(11)
Marginal distribution m
n
and the resulting sample
size depend on the exponent a
0
of power prior.
Owing to lack of operational interpretation and
without a way to assess the value of a
0
, the use of
power prior for posterior inference has been
criticized, for instance, (Spiegelhalter et al., 2004).
De Santis (2007) gave out two interpretations for
using power prior in the parameter inference of
independent and identically distributed (IID) data:
When a maximum likelihood estimator for θ
exists and is unique, π
P
is equivalent to a
posterior distribution that is obtained by using
a sample of size
00
ran
, which provides the
same maximum likelihood estimator for θ as
the entire sample.
When the model (| )
n
f
belongs to the
exponential family, the prior π
P
for the natural
parameter coincides with the standard
BayesianSampleSizeOptimizationMethodforIntegratedTestDesignofMissileHitAccuracy
247
posterior distribution that is obtained by using
a sample of size
00
ran whose arithmetic
mean is equal to the historical data mean.
Hence, at least in some standard problems, a power
prior can be interpreted as a posterior distribution
that is associated with a sample whose informative
content on θ is qualitatively the same as that of the
historical data set, but quantitatively equivalent to
that of a sample of size r. In the design of integrated
test for missile hit accuracy, an intuitive idea is to
choose directly the simulation system credibility C
0
as exponent a
0
for power prior calculation. However,
considering the exponential behaviour of likelihood
function for normal random variable, the obtained
power prior with extremely large size of prior
samples via expression (10) could be a very sharp
distribution, which means the design prior of field
test already meets with the Bayesian SSD criteria as
APVC, ALC and LPC. So, we don't need to carry
out any field test for inference of interested
parameter. Obviously, this is impractical, as with
low simulation credibility, performance inference
can takes on high risk even with large size of
simulation test samples.
The above contradictory is caused by ignoring
the influence of prior sample size n
0
on determining
the exponent a
0
of power prior. Taking C
0
= a
0
, the
prior sample size n
0
can still have great influence on
the equivalent standard sample size according to
00
ran , which makes the design prior impractical.
For this reason, we propose the design effect of test,
which can be used to get equivalent sample size n
r
of
simulation test samples based on the notion of
design effect equivalence, and hence get a rational
design prior of Bayesian SSD.
3.2 Design Effect of Test
Design effect of test is proposed with a
comprehensive consideration on test credibility and
posterior estimation performance. Taking average
posterior variance of Bayesian SSD as the posterior
estimation performance, it is defined as
APV
exp( )
E
DC L (12)
Where, C indicates test credibility, L
APV
denotes the
average posterior variance of interested parameter
obtained with non-informative prior and test samples.
If simulation test has a credibility C
0
, and with a
sample size n
0
, it takes on equal design effect as
field test (whose credibility is 1) with a sample size
n
r
, then we choose the exponential factor a
0
=n
r
/n
0
for power prior calculation. Thus, according to De
Santis's interpretation, we get the equivalent sample
size (ESS) n
r
for simulation test samples of size n
0
with equal informative content on θ.
From equation (12), while C
0
=1, prior samples
is equal to actual field test samples, and a
0
=1; if
simulation test credibility C
0
is low, even though
sample size n
0
is very large, and L
APV
→ 0, as its
design effect D
E
→C
0
, the ESS n
r
would only be a
limited value. Taking non-informative prior as
analysis prior, and s
0
=s
1
=1.2, exponent a
0
of power
prior under different simulation credibility can be
worked out based on equivalence of test design
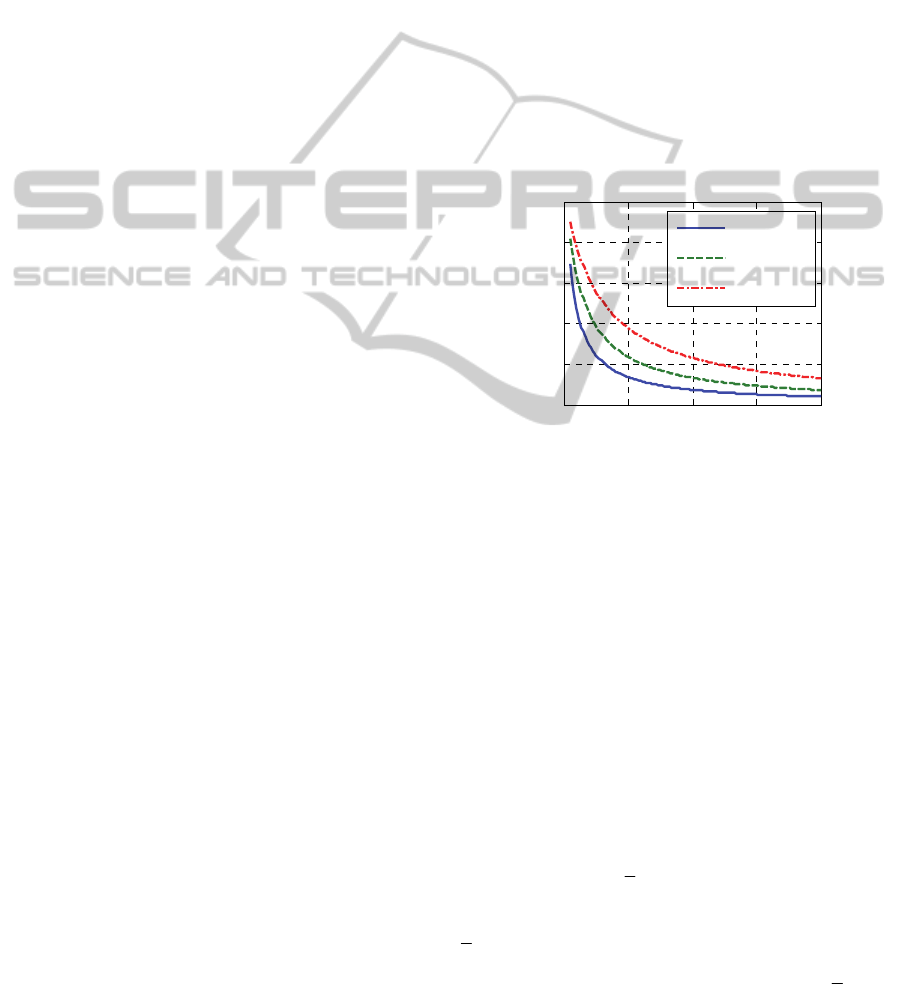
effect. Figure 1 shows its relationship with
simulation test sample size n
0
. In this way, exponent
a
0
of power prior decreases with the increment of
simulation test sample size n
0
, which avoids the
above-mentioned assessment risk with only large
numbers of simulation test samples.
0 50 100 150 200
0
0.2
0.4
0.6
0.8
1
Power exponent a
0
Simulation sample size n
0
C
T
= 0.8
C
T
= 0.9
C
T
= 0.95
Figure 1: Power exponent a
0
vs. simulation test sample
size n
0
.
3.3 Equivalent Sample Size based
Design Prior Elicitation
In the integrated test of missile hit accuracy, mean
value μ of impact point is taken as parameter of
interest, simulation test samples
00
1
[, , ]
nn
zz z
and field test samples
1
[, , ]
rr
nn
yy y
are
independent identically distributed (IID) normal
random variables, with both mean value μ and
precision λ (reciprocal of variance σ
2
) unknown.
Then, we can get the posterior distribution of μ from
simulation test samples with non-informative
analysis prior , which is expressed as
00
2
000 0
(| ) St(| ,( 1) , 1), 1
nn
zn sn n
z
Where, St express student t distribution;
0
mean( )
ni
zz
is estimated location parameter;
2
00
(1)ns
is precision, with
0
22
0
mean ( )
in
szz;
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
248
n
0
-1 is the degree of freedom for student t
distribution. So, the average posterior variance of μ
can be derived as
00
2
0
APV
0
(| ) Evar(| )
1
nn
s
L
n
zz
With non-informative prior, suppose field test
samples of size n
r
take on equal design effect as
simulation test samples of size n
0
, the computational
formula of equivalent sample size is
2
2
0
0
0
exp exp
11
r
r
s
s
C
nn
And, it follows that
22
0000
2
00 0
(1) (1)ln()
(1)ln()
r
r
nssn C
n
sn C
(13)
Where, s
r
is standard deviation of field test samples.
In test design stage, both s
0
and s
r
are unknown, we
can take s
r
=s
0
provided a homogeneity of variance
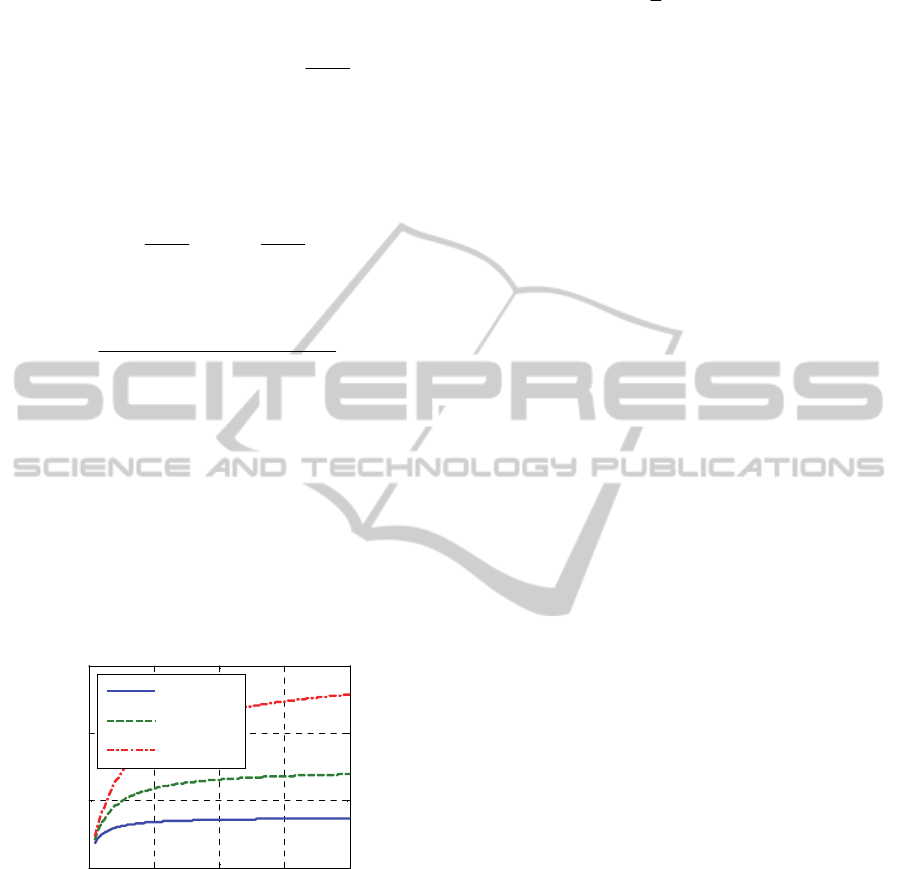
assumption. Figure 2 shows the relationship of
equivalent sample size n
r
and simulation test sample
size n
0
under different simulation test credibility,
with s
r
=s
0
=1.2. It can be seen that the ESS tend to
finite value as the increase of simulation sample size,
and the higher the simulation credibility, the larger
the equivalent sample size, which coincides with
practical situation.
0 50 100 150 200
0
10
20
30
Equivalent sample size n
r
Simulation sample size n
0
C
T
= 0.8
C
T
= 0.9
C
T
= 0.95
Figure 2: Equivalent sample size of simulation test
samples.
Following De Santis's conclusions, as long as we get
the equivalent sample size of simulation test samples
0
n
z
, which is IID and normally distributed, the
design prior for Bayesian SSD of subsequent field
test can be expressed as
0
000
000
(, | ) Ng(, | , , , )
N
(| , )Ga(| , )
nr
r
pn
n
z
(14)
Where,
0
0
0
2
00
(1)/2
/2
n
r
r
z
n
ns
4 SSD FOR INTEGRATED TEST
SCHEME
The purpose of SSD for integrated test of missile hit
accuracy is to get a comprehensive test scheme
satisfying the requirement of assessment precision
with minimal test cost. In this section, we take
average posterior variance of missile hit accuracy as
assessment precision, and give out the optimal SSD
methods for integrated test under both test cost
constraint and required assessment precision
constraint, according to Bayesian average posterior
variance criterion.
4.1 Purpose for Optimal Design of
Integrated Test Scheme
Design of integrated test scheme takes on the
objective of deciding sample sizes of both
simulation test and field test for optimal assessment
of missile hit accuracy. So we can avoid resources
waste caused by excessive sample size and also
assessment risk due to insufficiency of test samples.
Therefore, optimal design of integrated test takes on
two purposes: first, determining sample size
allocation plan for simulation test and field test to
get a minimal Bayesian average posterior variance
of missile hit accuracy under limited test cost
constraint; second, making unified sample size
allocation plan for simulation test and field test, to
meet the requirement of posterior estimation
precision with minimal test cost.
In allusion to integrated test of missile hit
accuracy, we want to get a scientific estimation for
mean value μ of impact point, whose precision can
be expressed with posterior variance. So, optimal
design of integrated test scheme will be studied from
two aspects as devoted test cost and estimated
average posterior variance, with an objective of
getting optimal sample size allocation plan for
integrated test scheme under two kinds of constraints.
BayesianSampleSizeOptimizationMethodforIntegratedTestDesignofMissileHitAccuracy
249

4.2 Bayesian SSD based on APVC
The problem can be formalized as follows. Take
equation (14) as design prior of field test, while we
get field test samples x
n
, mark mean( )
i
x
x ,
22
mean ( )
i
s
xx
, then, the posterior
distribution of μ is
1
00
1
0
2
12
00
(| ) St ,( )( 2) ,2
()( )
1
()( )
22
nnr n
nr r
nrr
pnnnn
nn n nx
ns
nnnn x
x
It follows that the posterior variance of μ is
0
var
()( 2)
n
n
r
nn n
x (15)
As field test sample x
n
is unknown, and can be seen
as random variable. So, in order to get the average
posterior variance of μ, marginal distribution (11) of
field test sample x
n
is used in mean value calculation,
and it follows that
0
E( )
Evar( | )
()( 2)
n
n
r
nn n
x (16)
In this way, average posterior variance of μ is a
function of E(ns
2
) and
2
0
E( )
x
. Where, ns
2
has
a Gamma-Gamma distribution, and
x
has a student
t distribution, Bernardo (Bernardo and Smith 2000)
gave out their probability distribution function as,
22
00
()Gg ,2,(1)/2pns ns n
(17)
11
00 0 00
() St , ( ) ,2px x nnn n
(18)
From equations (13) to (18), we can get the average
posterior variance of μ
22
0
(4) 1
E[var( )]
( 1)( )( 1)( 3)
rr r
n
rrrr
ns n n n n
nn nn n n
x
(19)
Given the required ε in APVC, we can get the
minimal field test sample size n* according to
equation (19), which meets with the requirement of
APVC.
4.3 Optimal Design Equations of
Integrated Test Scheme
Suppose unit sample costs for simulation test and
field test are u
0
and u
1
respectively. Under the
constraint of total test cost within T
c
, we can get the
optimal integrated test scheme with minimal average
posterior variance of interested parameter based on
APVC of Bayesian SSD, whose design equation is
as follows:
APV 0 0
0
00 1
0
(, ,) Evar(| )
min
[,]
s.t. 1;
1;
n
c
LCs
nn
nu nu T
n
n
Nx
N
(20)
Where, L
APV
(N, C
0
, s
0
) represents Bayesian average
posterior variance of missile hit accuracy, and works
as the objective function of optimization, which is
denoted by equation (19). N is the optimizing vector
containing sample sizes of simulation test and field
test. C
0
is simulation test credibility. s
0
is standard
deviation of simulation test samples.
The other condition for optimal design of
integrated test scheme is under required precision ε
constraint in APVC, seeking the sample size
allocation (SSA) plan for minimal total test cost. At
this time, the optimal design equation is
00 1
APV 0 0
0
min ( )
(, ,) ;
s.t. 1;
1
c
Tnunu
LCs
n
n
N
N
(21)
Equations (20) and (21) provide the optimal design
methods for integrated test scheme of missile hit
accuracy, whose usage will be demonstrated in
detail in Section 5 with two illustrative examples.
During their utilization, we get equivalent sample
size of simulation test samples for design prior based
on credibility C
0
and standard deviation s
0
. So,
optimal design scheme of integrated test can be
obtained in consideration of two kinds of unit
sample cost.
5 ILLUSTRATIONS
In the test and evaluation of missile hit accuracy, the
key point of integrated test design is to decide the
sample size allocation plan for simulation test and
field test. So, we can get optimal assessment
precision with minimal test consumption. In this
section, we demonstrate the optimal design of
integrated test scheme under constraints of cost and
required assessment precision. In this way, the
effectiveness of Bayesian SSD method for design of
integrated test is illustrated, where the basic settings
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
250
for simulation test and field test are shown in Table
1 (not real number, just used for illustration).
Table 1: Basic setting for test schemes.
Test type
Unit sample
cost ($)
Pre-estimated
standard
deviation
Credibility
(C
T
)
Simulation 50 1.2 0.70~0.95
Field 2000 1.2 1.0
5.1 Optimal Design with Cost
Constraint
Suppose we have a total appropriation budget T
C
=20, 000 $, and want to get the optimal missile hit
accuracy assessment. Optimization equation for SSA
of integrated test can be built according to (20),
whose solution is straight forward using a nonlinear
constrained optimization algorithm. Thus, we get
optimal sample size allocation plans under different
simulation credibility (SC), where n
0
and n
1
are
sample sizes for simulation test and field test
respectively, as shown in Table 2. Obviously, the
ratio of simulation test samples in optimal integrated
test scheme and the corresponding equivalent
sample sizes increase with simulation credibility.
Meanwhile, average posterior variances decrease
with simulation test credibility, which indicates the
precision of Bayesian posterior assessment is better
under higher simulation test credibility.
Table 2: Optimal integrated test schemes under cost
constraint.
SC SSA ESS APV
C
0
n
0
n
1
n
r
L
APV
0.70 80 8 4.8410 0.2321
0.80 80 8 6.9659 0.1407
0.90 80 8 12.6516 0.0813
0.95 160 6 24.8609 0.0494
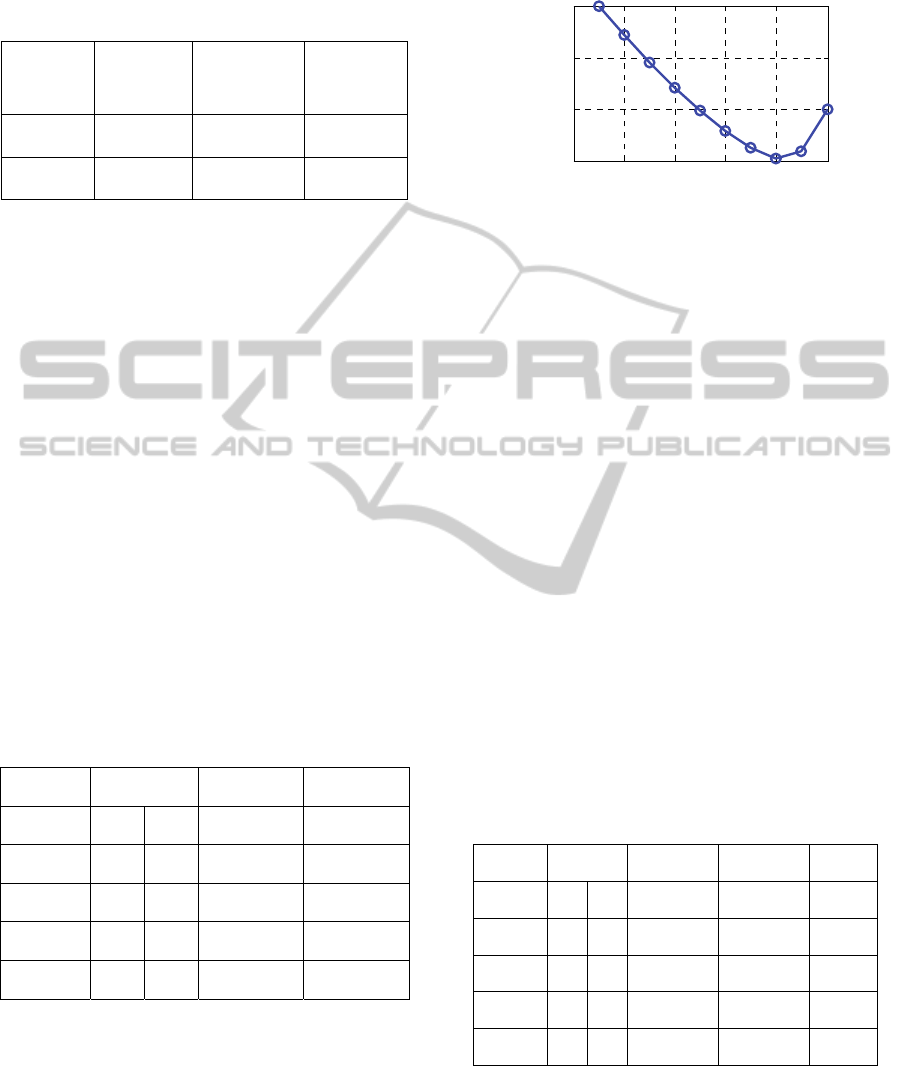
Figure 3 shows the relationship between field test
sample size n and average posterior variance under
total test cost constraint with a simulation test
credibility C
0
=0.8, where simulation test sample size
is determined by the residual fund of field test. In
this way, integrated test with combined use of
simulation test and field test takes on better
assessment effect than traditional only with field test
samples mode.
0 2 4 6 8 10
0.16
0.18
0.2
Field test sam
p
le size n
APV
Figure 3: Average posterior variance vs. field test sample
size.
5.2 Optimal Design with Required
Precision Constraint
Suppose we expect an assessment precision of ε=0.1
(take APVC here) for missile hit accuracy,
optimization goal is to get an integrated test scheme
with minimal cost. Thus, optimization equation for
SSA of integrated test can be built according to (21),
and optimal SSA plan under different simulation test
credibility can be obtained using a nonlinear
constrained optimization algorithm, as shown in
Table 3. In this way, under APVC constraint, sample
size of field test in optimal test scheme is on the
decrease as simulation credibility increases, and
meanwhile the total cost for integrated test scheme is
decreasing. Exponent of power prior (EoPP) a
0
become larger and larger as the increment of
simulation credibility C
0
, which indicates simulation
test samples with higher credibility take on greater
weight in posterior assessment. Thus, less field test
samples are needed, and total test cost is reduced.
Table 3: Optimal integrated test schemes under required ε
in APVC.
SC SSA EoPP APV TC
C
0
n
0
n
1
a
0
L
APV
T
C
0.70 88 30 0.0552 0.1000 64400
0.80 65 16 0.1056 0.0999 35250
0.90 101 3 0.1290 0.0999 11050
0.95 25 2 0.5576 0.0985 5250
Note that with a given ε=0.1, classical SSD method
gives a number of 16. So we can see that with low
simulation test credibility (as C
0
=0.7, 0.8),
integrated test scheme show no predominance,
which is due to the negative influence on Bayesian
BayesianSampleSizeOptimizationMethodforIntegratedTestDesignofMissileHitAccuracy
251

posterior assessment brought by poor prior
information. This fact also indicates that if
distribution difference of simulation test samples
and field test samples is big (namely simulation test
takes on low credibility), classical design of
experiment and assessment method without
consideration on prior information could be more
rational. While simulation test credibility is high,
adopting integrated test scheme improves test
efficiency greatly by saving a great deal of test cost.
In Table 4, we give out several designed test
schemes satisfying the required precision ε=0.1 in
APVC, where the simulation test credibility is 0.9. It
is thus clear that as the increase of simulation test
sample size, exponential factor a
0
of power prior
decreases, and equivalent sample size tend to finite
value. Thus, it would not happen that design prior
obtained with large number of simulation test
samples has already met with Bayesian SSD criteria,
which avoids the credibility risk of posterior
assessment for parameter of interest. So, we can see
the rationality of equivalent sample size, which is
obtained based on equal test design effect.
Table 4: Test schemes for required ε=0.1 in APVC with
C
0
=0.9.
SSA ESS EoPP APV TC
n
0
n
1
n
r
a
0
L
APV
T
C
187 2 13.7318 0.0734 0.1000 13350
101 3 13.0240 0.1290 0.0999 11050
68 4 12.3517 0.1816 0.0998 11400
50 5 11.6866 0.2337 0.0999 12500
40 6 11.1206 0.2780 0.0995 14000
32 7 10.4854 0.3277 0.0999 15600
27 8 9.9583 0.3688 0.0997 17350
6 CONCLUSIONS
The paper considers SSD problem for integrated test
design of missile hit accuracy. Power prior is used in
weighted fusion of simulation test samples, and ESS
of simulation test based on equal test design effect is
proposed to get the design prior of Bayesian SSD for
field test. Thus, an advanced Bayesian solution, with
systematic and scientific planning concept, for SSA
problem in design of integrated test scheme is
obtained, which takes on the following features:
(1) SSD is realized by Bayesian pre-posterior
calculation. A reasonable estimation for posterior
distribution of interested parameter θ can be
obtained with comprehensive usage of historical
data and prior information before actual field test.
Hence, minimal sample size for required assessment
precision can be worked out.
(2) Calculation method for ESS of simulation
test is given out based on the idea of power prior and
test design effect, which get an equivalency of large
number of low credible simulation test samples with
limited standard filed test samples. Thus, we avoid
the discrepancy that taking simulation credibility
directly as exponent of power prior, design prior
obtained from large numbers of simulation test
samples has already met with Bayesian SSD criteria.
And in this way, the assessment risk is reduced.
(3) Taking APV of missile hit accuracy as the
output, we get the optimization design equations for
integrated test scheme with Bayesian SSD method
under both test cost constraint and required precision
ε constraint in APVC. Thus, we give out a Bayesian
SSD method for integrated test design of missile hit
accuracy with optimal efficiency.
REFERENCES
Adcock, C. J., 1997. Sample size determination: a review.
Journal of the Royal Statistical Society: Series D (The
Statistician), 46(2), 261-283.
Balci, O., 1997. Verification validation and accreditation
of simulation models, 135-141., In Proceedings of the
29th conference on Winter simulation, Atlanta, GA,
USA.
Balci, O., 2013. Verification, Validation, and Testing of
Models, 1618-1627. In Gass, S., and Harris, C.M.,
eds., Encyclopedia of Operations Research and
Management Science. Springer, New York.
Bernardo, J. M., and Smith, A. F. M., 2000. Bayesian
theory. John Wiley & Sons, New York.
Clarke, B., and Yuan, A., 2006. Closed form expressions
for Bayesian sample size. The Annals of Statistics,
34(3), 1293-1330.
Claxton, J. D., Cavoli, C., and Johnson, C., 2012. Test and
Evaluation Management Guide, The Defense
Acquisition University Press. Fort Belvoir, VA. 6
th
Edition.
De Santis, F., 2004. Statistical evidence and sample size
determination for Bayesian hypothesis testing. Journal
of statistical planning and inference, 124(1), 121-144.
De Santis, F., 2007. Using historical data for Bayesian
sample size determination. Journal of the Royal
Statistical Society: Series A (Statistics in Society),
170(1), 95-113.
SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand
Applications
252

Di Bacco, M., Amore, G. D., Scalfari, F., De Santis, F., &
Pacifico, M. P., 2004. Two experimental settings in
clinical trials: predictive criteria for choosing the
sample size in interval estimation. Applied Bayesian
Statistical Studies in Biology and Medicine, 109-130.
Kluwer Academic Publishers, Norwell, MA, USA.
Desu, M. M., and Raghavarao, D., 1990. Sample Size
Methodology. Academic Press, Boston.
Fryback, D. G., Chinnis, J. O., and Ulvila, J. W., 2001.
Bayesian cost-effectiveness analysis. International
Journal of Technology Assessment in Health Care,
17(1), 83-97.
Greenhouse, J. B., and Waserman, L., 1995. Robust
Bayesian methods for monitoring clinical trials.
Statistics in Medicine, 14(12), 1379-1391.
Ibrahim, J. G., Chen, M. H., and Sinha, D., 2003. On
optimality properties of the power prior. Journal of the
American Statistical Association, 98(461), 204-213.
Ibrahim, J. G., and Chen, M. H., 2000. Power prior
distributions for regression models. Statistical Science,
15(1), 46-60.
Joseph, L., Du Berger, R., Belisle, P., and Others., 1997.
Bayesian and mixed Bayesian/likelihood criteria for
sample size determination. Statistics in Medicine,
16(7), 769-781.
Joseph, L., Wolfson, D. B., and Du Berger, R., 1995.
Sample size calculations for binomial proportions via
highest posterior density intervals. The Statistician,
44(2), 143-154.
Joseph, L., and Belisle, P. 1997. Bayesian sample size
determination for normal means and differences
between normal means. Journal of the Royal
Statistical Society: Series D (The Statistician), 46(2),
209-226.
Kraft, E. M., 1995. Integrated Test and Evaluation- A
knowledge-based approach to system development., In
1st AIAA Aircraft Engineering, Technology, and
Operations Congress. AIAA 95-3982, Los Angeles,
US.
Kushman, K. L., and Briski, M. S., 1992. Integrated test
and evaluation for hypervelocity systems. In AIAA
17th Aerospace Ground Testing Conference.
American Institute of Aeronautics and Astronautics,
Nashville, TN.
Murphy, K. R., Myors, B., and Wolach, A. H., 2009.
Statistical power analysis: A simple and general
model for traditional and modern hypothesis tests.
Routledge, New York, NY.
Nassar, M. M., Khamis, S. M., and Radwan, S. S., 2011.
On Bayesian sample size determination. Journal of
Applied Statistics, 38(5), 1045-1054.
Rebba, R., Mahadevan, S., and Huang, S. P., 2006.
Validation and error estimation of computational
models. Reliability Engineering & System Safety,
91(10-11), 1390-1397.
Reyes, E. M., and Ghosh, S. K., 2013. Bayesian Average
Error-Based Approach to Sample Size Calculations for
Hypothesis Testing. Journal of Biopharmaceutical
Statistics, 23(3), 569-588.
Schwartz, M., 2010. Defense acquisitions: How DoD
acquires weapon systems and recent efforts to reform
the process. Paper presented at the Congressional
Research Service, Washington, DC.
Spiegelhalter, D. J., Abrams, K. R., and Myles, J. P., 2004.
Bayesian approaches to clinical trials and health-care
evaluation. John Wiley & Sons, Ltd, Chichester, West
Sussex, England.
Spiegelhalter, D. J., and Freedman, L. S., 1986. A
predictive approach to selecting the size of a clinical
trial, based on subjective clinical opinion. Statistics in
medicine, 5(1), 1-13.
Wang, F., and Gelfand, A. E., 2002. A simulation-based
approach to Bayesian sample size determination for
performance under a given model and for separating
models. Statistical Science, 17(2), 193-208.
Waters, D. P., 2004. Integrating Modeling and Simulation
with Test and Evaluation Activities. In USAF
Developmental Test and Evaluation Summit.
Woodland Hills, California: AIAA 2004-6800.
Weiss, R. 1997. Bayesian sample size calculations for
hypothesis testing. Journal of the Royal Statistical
Society: Series D (The Statistician), 46(2), 185-191.
BayesianSampleSizeOptimizationMethodforIntegratedTestDesignofMissileHitAccuracy
253
