Experimental/FEM Optimization of Medium Voltage Rubber

Insulated Electric Cables Vulcanized with Steam Water

Numerical Simulations and Inverse Analyses

Gabriele Milani

and Federico Milani

Technical University in Milan, Piazza Leonardo da Vinci 32, 20133, Milan, Italy

CHEM.CO Consultant, Via J.F.Kennedy 2, 45030, Occhiobello (RO), Italy

Keywords: Power Cables Production Lines, Steam Curing, FE Evaluation of Temperature Profiles, Genetic Algorithm.

Abstract: A comprehensive combined numerical model based on Genetic Algorithm (GA) optimization and heat

transfer Finite Element computations is presented. The numerical analyses are carried out to evaluate the

final crosslinking degree of a medium voltage electric cable subjected to industrial peroxide reticulation.

The final task is to minimize the difference between numerically predicted and experimentally determined

crosslinking degree along the thickness of the insulator, when a variable steam temperature profile along the

pipe length is assumed to explain the unexpected under-vulcanization of the cable in the internal layers. To

minimize the gap between experimentally determined curing degree and numerical predictions, a Genetic

Algorithm (GA) optimization is used.

1 INTRODUCTION

In a companying paper (Milani and Milani 2015), a

real production line 103 meters long has been

analyzed from an experimental point of view.

Experimental Differential Scanning Calorimetry

(DSC) results shown that, at four different

vulcanization conditions with steam, the resulting

reticulation degree at the end of the production

process is sensibly lower than that expected from

simplified evaluations based on the knowledge of

the half time life of the peroxides used, especially

when the steam temperature is low and the exposure

time is reduced. The situation is critical in the

internal layers.

The present paper is aimed at analyzing the

vulcanization process from a numerical point of

view, trying to identify the reasons at the base of

such an unexpected under-vulcanization of the cable.

The Finite Element analysis of the heat transfer

process during rubber vulcanization has long

tradition and has been successfully applied by many

authors to predict the reticulation degree at the end

of several different production processes Lenir

(1984) and Kosar and Gomzi (2007).

In this framework, the combined approach

proposed in the present paper may be regarded as

innovative and beneficial for producers interested in

a quantitative evaluation of the level of cure

obtained in the production process.

The input parameters optimization is performed

by means of an inverse analysis with a non standard

meta-heristic approach based on Genetic Algorithm

concepts. The procedure appears particularly

appealing instead of the utilization of gradient based

routines into a standard least squares minimization

on experimental data, because the crosslinking

density function at the end of the industrial process

is not analytically known.

At fixed input parameters, the determination of

the curing level is typically obtained by means of

Finite Element simulations.

When FEs are used to determine the crosslinking

degree of the cable with constant vulcanization

temperature, a partial match between numeric

predictions and experimental evidences from DSC is

found, indicating a clear discrepancy between set

parameters and real values. Such result suggests that

the steam curing temperature along the pipe length

probably decreases, at the same time addressing that

one of the key input parameters to optimize in the

GA is the variable steam temperature.

Individuals of the GA are represented by the

temperatures at different positions of the pipe,

Milani G. and Milani F..

Experimental/FEM Optimization of Medium Voltage Rubber Insulated Electric Cables Vulcanized with Steam Water - Numerical Simulations and Inverse

Analyses.

DOI: 10.5220/0005503100270035

In Proceedings of the 5th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH-2015),

pages 27-35

ISBN: 978-989-758-120-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

-a

-b

Figure 1: Schematic representation of the vulcanization

process of a wire. -a: heating phase. –b: cooling phase.

whereas the objective (fitness) function is represent

by the sum of the squared difference between

numeric prediction and experimental determination

of the crosslinking degree. The proposed GA is

robust and non-standard, based on a specifically

developed zooming strategy which consists in the

subdivision of the population at each iteration into

two sub-groups, depending on individuals grade of

fitness (elitist strategy). Different genetic procedures

are applied to the sub-groups, namely both two

typologies of admissible mutations for the elite sub-

population and mutation and reproduction for the

remaining individuals. In order to improve algorithm

convergence, a user-defined population percentage,

depending on individuals fitness, is replaced with

new phenotypes at the end of each iteration,

enforcing in this way the chromosomes renewal.

The aim of the numeric approach proposed is not

only to fit experimental data through least squares

best fitting, but also to suggest a simple and efficient

computational tool able to determine the expected

level of crosslinking.

2 GOVERNING PARTIAL

DIFFERENTIAL EQUATIONS

The real production plant has to be idealized before

applying any mathematical model. At this aim, the

vulcanization process can be schematically

subdivided into two simply phases (Figure 1): (1)

heating zone and (2) a cooling zone.

Index

indicates the metallic conductor (semi-

diameter

) and index

indicates the insulation

width (ray

The axial symmetry of cable leads to a two

independent variables system: the distance

of an

insulation layer respect to cable axis and exposure

time

t . At constant cable speed, a cable section at a

distance

with respect to the starting point of the

production line, is characterized by an exposure time

equal to

uzt /



. This means

is a variable

dependent from t.

During the heating phase pressurized steam at

temperature is used, exchanging heat with Ethylene-

Propylene Diene Monomer Rubber (hereafter

abbreviated as EPDM for the sake of clearness)

surface mainly by convection. Fourier’s heat

equation law in cylindrical coordinates is used to

numerically determine temperature profiles along

cable thickness Milani and Milani (2008). For the

insulation layer the heat balance field equation is the

following:





































rpp



(1)

Where



and



are EPDM density, specific

heat capacity and heat conductivity respectively;



is the insulation specific heat of reaction;

is the rate of crosslinking;

The term



in equation (1) is the heat

produced by the decomposition of the peroxide.



depends both on type of peroxide used and on

type of hydrogen to extract (allylic, vinylic, etc.).

For simplicity, we assume a linear behavior for

with respect to concentration, i.e.



Similar considerations can be repeated for the

conductor, obviously assuming

0

z=u /t

steam water at

pressure

EPDM

Conductor (Al Cu)

Phase I

H O ambient temperature

Phase II

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications





0//1//

 rTrrTtTc



(2)

Where the index

refers to the conductor layer.

Since heat equation is of second order in space,

two boundary conditions must be specified. In

particular, for the problem at hand, at



symmetry condition on the temperature field is

imposed in the well-known form





 rT

whereas at

Rr 

we impose:



0, 



radnpp

qTtRTh



(3)

Where

is the heat transfer coefficient between

EPDM and steam,

is steam temperature and

rad

is the heat flux transferred by radiation. Here it

is worth noting that, in the present case (i.e. for

vulcanization with steam), the evaluation of

rad

would be a rather difficult task. As a matter of fact,

the well-known radiation formulas in polar

coordinates cannot be applied rigorously since the

water vapor participates in the radiation exchange

between the tube wall and insulation surface. Since

typical values of the convection coefficient are used

for the steam condensation, radiation is not included

in the model due to the complexity of accurately

including the radiation effects.

Finally, at the interface between conductor and

insulation, an equilibrium equation on the heat flux

exchanged is imposed in the form:









rtRTrtRT

ppjj

 /,/,



(4)

For transient conduction, heat equation is of first

order in time, requiring the assumption of an initial

temperature distribution:



pjp

RrRTrT

RrTrT





00,

(5)

No differences occur in the cooling zone, except

that boundary equation (3) is replaced by a pure

convection equation



0, 



wpwp

TtRTh



where

is the water heat transfer coefficient and

is the water cooling temperature.

Initial temperature conditions are obtained from

the profile evaluated at the last step of the cooling

zone, i.e. at





trT ,

, where

ccc

uLt /

with

curing zone length.

Figure 2: Schematic representation of the numeric

procedure adopted to determine final tensile strength of

each layer.

3 NUMERIC PREDICTIONS

UNDER CONSTANT

TEMPERATURE PROFILES

CONDITIONS

The determination of temperature profiles across

cable section does not require inverse analysis

optimization, but simply the Finite Elements

solution of problem (1)-(5), as illustrated

schematically in

Figure 2 when a temperature profile

for the vulcanization agent (stem), i.e. an individual

within a Genetic Algorithm scheme (GA, see after),

is considered .

Numerically estimated temperature profiles and

residual unreacted peroxide concentrations in one

vulcanization conditions experimentally tested is

represented in Figure 3.

In subfigure –a the temperature profiles at

constant steam temperature are represented. In

subfigure –b the reacted peroxide concentration of

internal middle and external layers are depicted,

whereas a comparison between simulated and

experimental data is provided in subfigure -c.

The data show a great diversion between the

deduced percentage of unreacted peroxides and the

experimental evidences.

Individuals generation

Step 0

Temperature profile

evaluation for each

insulator layer

Step 1

i=1,...,N

ind

z , t=z/u

Step 2

Best fitting on

experimental DSC

data

cable

thickness

Subdivision of the

insulator in layers

Repeat for each layer

Step 3

Repeat for each individual

Individuals fitness

evaluation

Vulcanization agent

concentration for each

insulator layer

Kinetic

model &

Kinetic

constants

evaluation

For each layer identification of the ureacted peroxide

concetration at the end of vulcanization

Experimental/FEMOptimizationofMediumVoltageRubberInsulatedElectricCablesVulcanizedwithSteamWater-

NumericalSimulationsandInverseAnalyses

-a

-b

-c

Figure 3: Test #1. –a: temperature profiles at water steam

constant temperature. -b: evolution of peroxide reaction in

three positions of the cable. –c: comparison with

experimental data.

It can therefore be concluded that an inverse

analysis would be extremely useful to optimize and

control the final level of crosslinking of the cable.

4 THE GA APPROACH

PROPOSED FOR THE

OPTIMIZATION

When the temperature profile of the steam along the

line is not known, inverse analyses are needed to

determine the profile that allows the best fitting of

the final crosslinking level across the cable section.

Meta-heuristic approaches are particularly indicated

because the analytical function representing the

steam temperature variation along the length is

unknown.

The meta-heuristic approach utilized is a non-

standard and robust GA that has been already used

in the same or different contexts by the authors in

Milani and Milani (2007, 2008, 2009, 2011).

The core of the GA proposed is a set of standard

(reproduction, crossover and mutation) and non-

standard (zooming and elitist strategy) genetic

procedures. The iterative optimization strategy is

schematically shown in

Figure 2. Each individual

population belonging is represented by admissible

temperature

of the steam on a series of control

nodes i along the length of the vulcanization pipe.

The main novel characteristic of the proposed GA

consists in the subdivision of the population into two

subgroups with improvement of the best fitness

individuals with zooming , Milani (2013) , Kang and

Zong (2004) and Haupt and Haupt (2004). An

admissible initial population





admissible|,...,1:

iindi

xNix



is randomly

generated In the in Step 0 at the first iteration. In

Step 1,

fitness





is evaluated solving for

each layer a PDEs system with fixed

. In Step 2,

two sub groups are created, namely





admissible|,...,1:

ieliti

xNix



and





elitindi

NNiy 







:,...,1:xxy

is the

group of all the individuals with the

elit

(user

defined) higher fitness values. This step represents

the zooming strategy. In Step 3a for each

random improvement of the individual (in terms of

fitness) is tried using a mutation operator. The

recursive double operation applied randomly

mut

times, leads to a new individual generation

which overwrites the original

only if its fitness





is greater than



. At the end of the

double loop, a new sub-group





admissible|,...,1:

iMelitiMM

xNix



obtained.

In Step 3b a mutation loop is applied randomly

mut

times for each individuals

with low fitness,

leading to an improvement of

fitness. The new

individuals

overwrite the original

only if

their fitness is greater than

one (elitist approach).

0.7

0.8

0.9

0.2

0.4

0.6

0.8

Cooling

Length L [m]

Heating

ormalized Temperature profile T(t,r)/T

Distance r [cm]

0 20 40 60 80 100 120

100

tube length [m]

Reacted peroxide [%]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

At the end of the double loop, a new sub-group





admissible|,...,1:

iMelitindiMM

yNNiy



y

is obtained. A classic reproduction operator is

applied only for individuals of

with high

fitness (i.e. on





elitind

NN 

parents with user

defined parameter



>1) in order to create a new

offspring group

. The remaining

 



elitind

NN 

individuals are generated

ex-novo using Step 0 procedure and are catalogued

into







admissible|/,...,1::

NjelitindNjN

cNNjc



c

vector.

-a

-b

-c

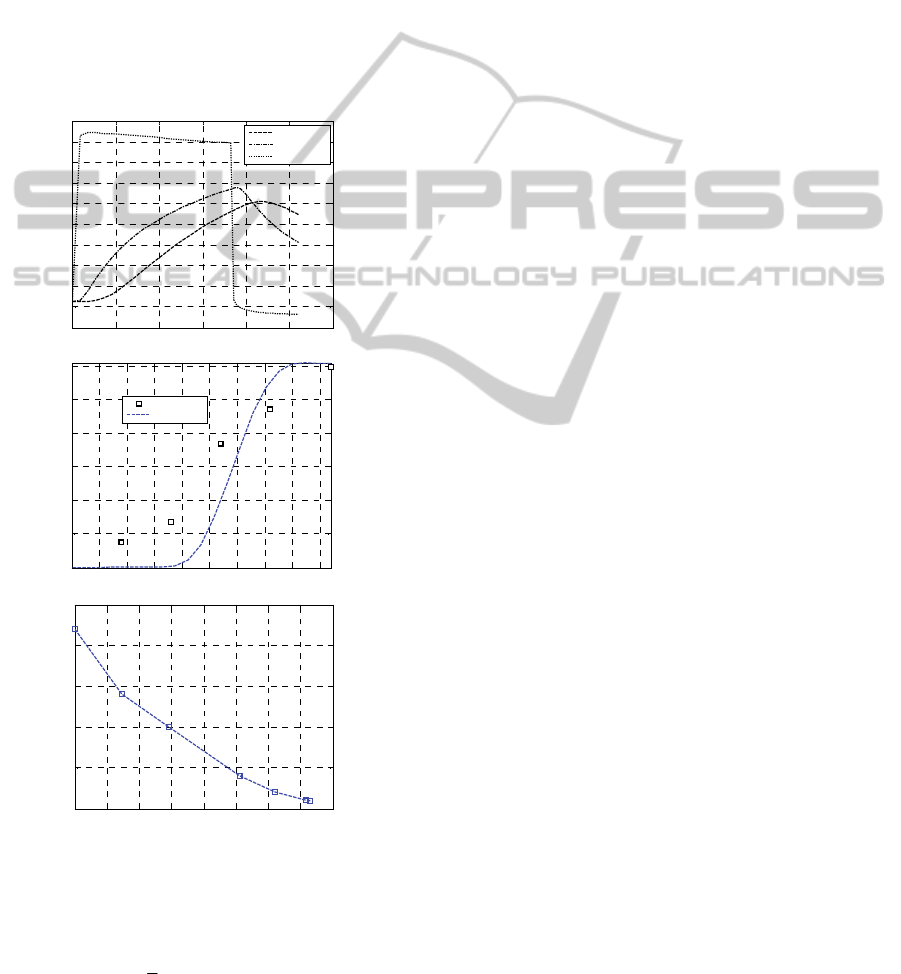
Figure 4: Test #1. –a: temperature profiles at variable

temperature. -b: comparison with experimental data on

unreacted peroxide %. –c GA temperature profile.

Finally, the last population at the

-th iteration is

collected into



ccxx 

and the procedure

is repeated from the beginning.

5 THE NEW SIMPLIFIED

MECHANISTIC MODEL

PROPOSED

The same electric cable subjected to the

aforementioned experimental tests is supposed to be

subjected to a variable steam pressure along the

vulcanization pipe to determine.

Results obtained for Tests from #1 to #4 are

shown from Figure 4 (#1) to Figure 6 (#4)-

Results for the best fitness individual at the last

GA iteration are reported assuming that the

individual best fits experimental DSC data.

The temperature profiles with variable steam

temperature are represented in subfigure –a (core,

middle, skin layers).

In subfigures –b the unreacted peroxide

concentration along cable thickness is shown (with a

comparison with DSC results), whereas in

subfigures –c the GA temperature profile along the

length is depicted.

Comparing simulations results it is possible to

note that:

1) there is a visible drop of temperature in Test #1,

which fully justifies the unsatisfactory

crosslinking level obtained during the

experimentation. Comparing the numerical

results with DSC experimental predictions, it is

clear that without this drop the crosslinking

should be close to optimal;

2) the minimization fitting function is non convex

and may provide multiple solutions. A similar

result may be obtained assuming a constant

steam temperature along the line. This remark

justifies also the utilization of a meta-heuristic

approach to deal with the problem at hand.

Standard minimization algorithms based on first

derivative evaluations may potentially fail in

finding the optimal solution.

The application of the GA combined with FEs

allows concluding that a drop of steam temperature

along the pipe length may be an important factor to

justify the unexpected under-vulcanization for

certain cure conditions, but such results do not

rigorously show conclusively that this is likely the

main cause.

0 20 40 60 80 100 120

100

120

140

160

180

200

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 10 20 30 40 50 60 70 80

180

185

190

195

200

205

tube length [m]

water steam temperature [°C]

Experimental/FEMOptimizationofMediumVoltageRubberInsulatedElectricCablesVulcanizedwithSteamWater-

NumericalSimulationsandInverseAnalyses

-a

-b

-c

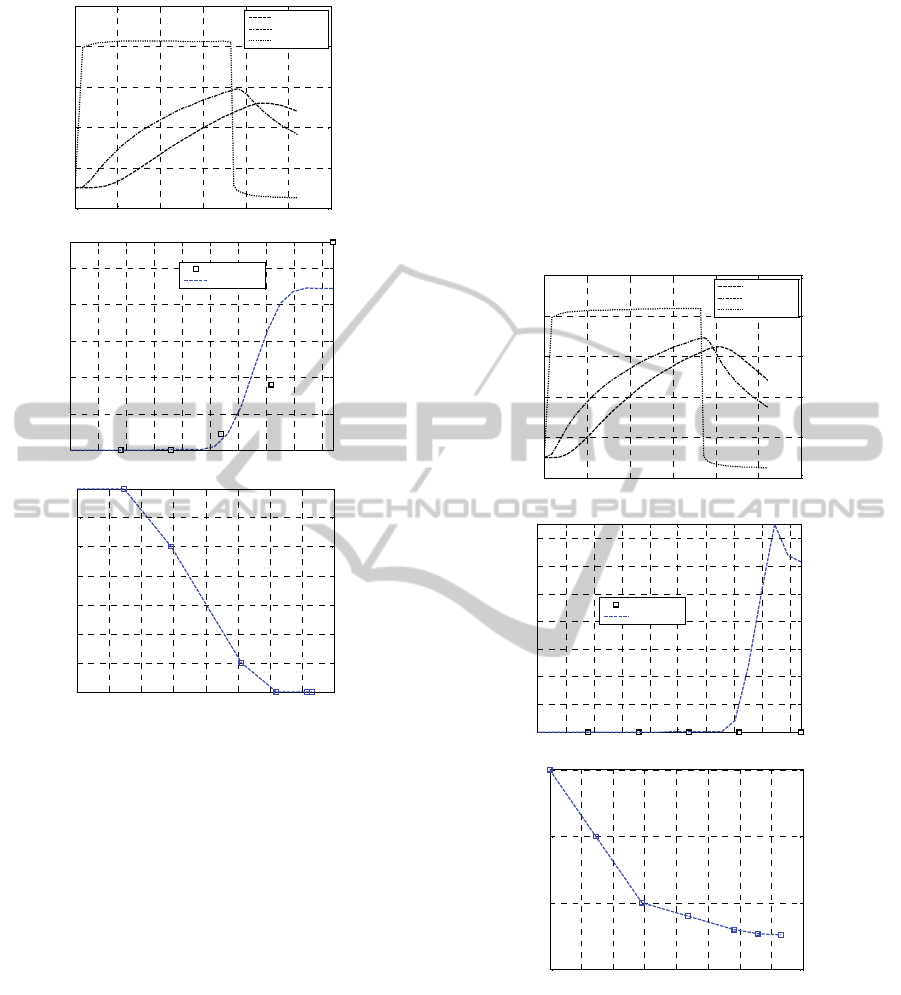
Figure 5: Test #2. –a: temperature profiles at variable

temperature. -b: comparison with experimental data on

unreacted peroxide %. –c GA temperature profile.

Before placing all of the cause for discrepancy

between the computed and experimental state of

cure profiles on an axial temperature decrease, it is

therefore interesting to have an insight into the effect

linked to a variation of the different coefficients

assumed constant in the FE computations.

In particular, it may be worth exploring the

effect of the values of the presumed heat transfer

coefficients and the initial temperature of the

insulation on the computed solutions on the

agreement with the experimental results.

In addition, the state of the steam in the

apparatus seems to indicate that the steam injected

into the tube is superheated. If this is the case, then

the expression for the relation between the

temperature and pressure for saturated vapor does

not apply. However, if the surface of the insulation

is below the saturation temperature of the steam at

the inlet pressure of the tube, then steam will

immediately condense on the surface of the

insulation at that temperature. Since the heat transfer

coefficient will be fairly high under these conditions

it might be reasonable to assume a constant surface

temperature equal to the saturation temperature, that

in Test #1 is 202°C for a pressure equal to 16.5 bar.

If the surface of the insulation is above this

temperature then the mode of heat transfer is simply

forced convection with the steam temperature

decreasing until the saturation temperature is

reached.

-a

-b

-c

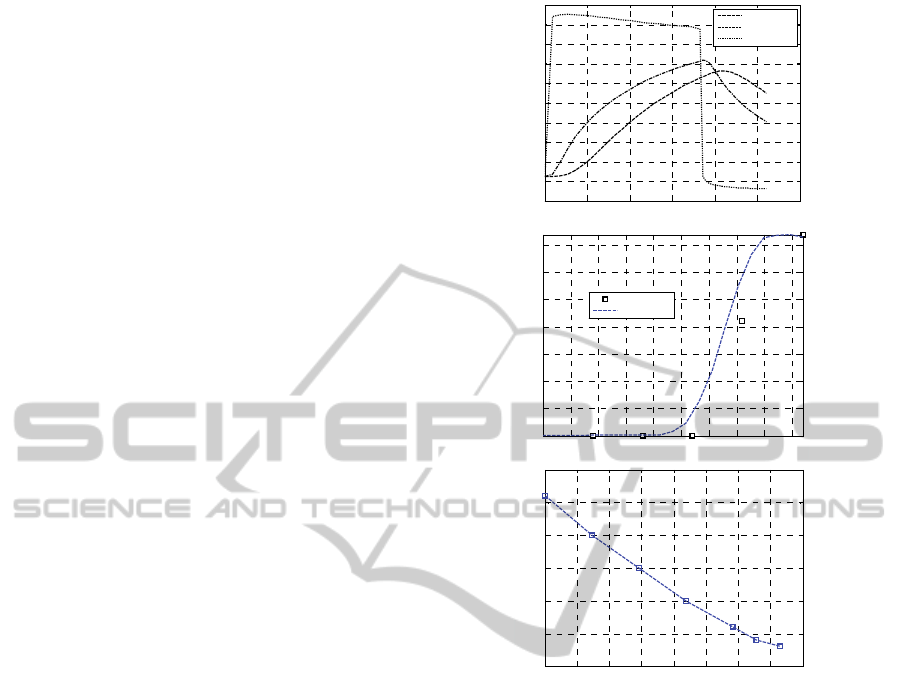
Figure 6: Test #4. –a: temperature profiles at variable

temperature. -b: comparison with experimental data on

unreacted peroxide %. –c GA temperature profile.

In order to take into account in a simplified

manner a complex problem of heat exchange, which

is unsteady, three additional sets of simulations are

performed assuming the following heat transfer

coefficients for the steam: h=30 W/m

K, h=300

W/m

K and h variable along the length of the pipe,

with and optimization of the heat transfer coefficient

0 20 40 60 80 100 120

100

150

200

250

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 10 20 30 40 50 60 70 80

208.5

209

209.5

210

210.5

211

211.5

212

tube length [m]

water steam temperature [°C]

0 20 40 60 80 100 120

100

150

200

250

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

x 10

-13

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 10 20 30 40 50 60 70 80

210.5

211

211.5

212

tube length [m]

water steam temperature [°C]

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

on experimental data by means of the same GA

approach previously used with variable steam

temperature. Such lower and upper bounds values

for h are assumed in agreement with indications

provided in Milani et al. (2008).

We assume steam temperature constantly equal

to T

=202°C and the total curing time t

equal to 5.6

minutes, i.e. design conditions of Test #1 are

investigated, being the vulcanization level in such

case critical and unexpectedly low. Whilst authors

are aware that a realistic numerical simulation

should take into account the variability of both T

and h, such simulations cannot be performed with

the GA approach proposed if a relation between h

and T

is not provided.

However, it is worth underlining that the

evaluation of h (especially as a function of T

) is a

very difficult task, especially when steam condenses

and there is a passage between vapor and liquid

phase, due to unknown heat unsteady transfer

processes. In addition, the common Newton’s law of

heat exchange by convection is probably too

simplistic and holds only for forced convection,

whereas probably in this case –as already pointed

out- there is an unknown dependence of h with the

temperature difference between steam and rubber

surface.

It is finally worth emphasizing that the values

adopted for h in the two sets of simulations with

constant h represent large bounds indicated for

steam in forced convection in many handbooks and

therefore such numerical analyses may well

approximate upper and lower bonds.

Temperature profiles obtained assuming lower

and upper bound constant values for h are depicted

in Figure-a and –b respectively. Furthermore, in

Figure-c the same results are represented with a

variable h values. The numerical prediction of the

unreacted peroxide along the thickness of the cables,

with a comparison with experimentally determined

values is finally reported in Fig. 9.

As can be noted, when a large value for h is

assumed (upper bound) the heat exchange is

intuitively favored and the % unreacted peroxide

found numerically sensibly deviates from

experimental values.

The same applies for an excessively reduced

value of h (lower bound). In such a condition, the

heat exchange between rubber surface and steam

becomes slow and the peroxide reacts with lower

velocity. The resultant % of unreacted peroxide is

therefore higher than that experimentally

determined.

-a

-b

-c

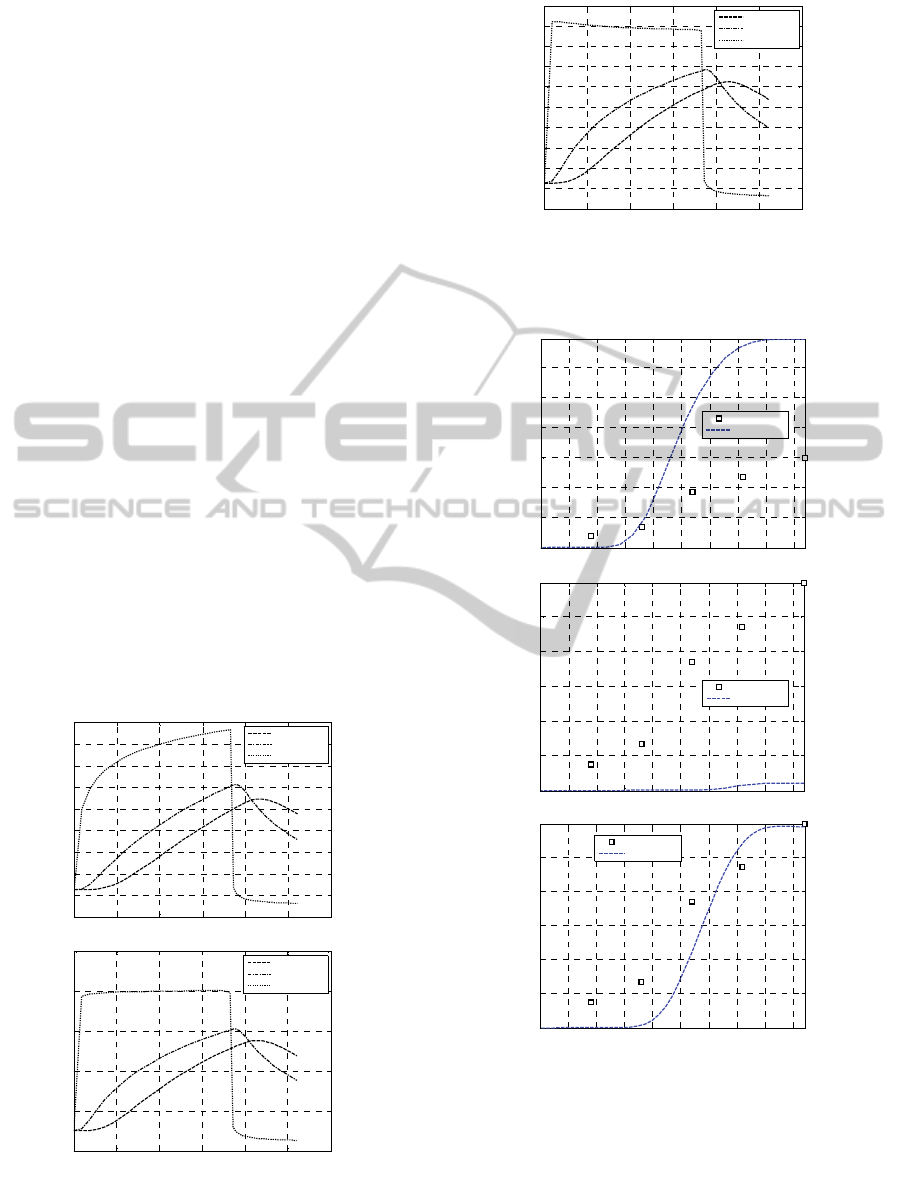
Figure 7: Test #3. –a: temperature profiles at variable

temperature. -b: comparison with experimental data on

unreacted peroxide %. –c GA temperature profile.

Conversely, result obtained assuming h as

variable are in quite good agreement with

experimental evidences, see Fig. 9-c. h profile along

the tube length determined by means of the GA

proposed is represented in Figure 10, with a 3D

representation of the unreacted peroxide % (along

the thickness and length of the cable). As can be

noted, there is a monotonic decrease of h, which

assumes very high values at the beginning

(superheating condition) and then decreases along

the line to typical values for steam water convection.

While the present simulations are obviously affected

by errors induced by the strong simplifications

assumed, the results obtained give interesting

information on the physical processes occurring to

the steam along the line.

It is finally interesting to notice that, when

dealing with the initial inlet temperature, GA

simulations are performed assuming a value equal to

25°C.

0 20 40 60 80 100 120

100

120

140

160

180

200

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

0.5

1.5

2.5

3.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 10 20 30 40 50 60 70 80

175

180

185

190

195

200

205

tube length [m]

water steam temperature [°C]

Experimental/FEMOptimizationofMediumVoltageRubberInsulatedElectricCablesVulcanizedwithSteamWater-

NumericalSimulationsandInverseAnalyses

Such value is certainly a lower bound and does

not take into account the initial heating phase inside

the extruder. Here it is only worth noting that to

provide realistic numerical simulations inside an

extruder is a very difficult task, involving 3D FE

modelling with coupled thermo-mechanical

approaches. Authors repeated some numerical

simulations adopting a simplified procedure, with an

increase of the curing temperature from 25 to 90°C

in the first 20 meters (length of the extruder) and

then starting the simulations. Results are reported in

Figure 10. As authors experienced, however, the

concentration of unreacted peroxide at the end of the

simulations (Figure 10-b) is very similar to that

found with an inlet temperature equal to 25°C.

6 CONCLUSIONS

A GA approach has been proposed to check and to

predict the behavior of a real production plant. The

general methodology has been validated analyzing

experimental evidences at the end of the production

process.

The mathematical approach proposed couples the

solution of the heat transmission law in cylindrical

coordinates with variable steam temperature and the

application of a Genetic Algorithm with inverse least

squares data fitting to determine the vulcanization

conditions of the samples.

-a

-b

Figure 8: Test #1. Temperature profiles obtained with

different values of

h. –a: lower bound for h –b: upper

bound for

h. –c: variable h.

-c

Figure 8: Test #1. Temperature profiles obtained with

different values of

h. –a: lower bound for h –b: upper

bound for

h. –c: variable h (cont.).

-a

-b

-c

Figure 9: Test #1. Unreacted peroxide % along the cable

thickness obtained with different values of

h. –a: lower

bound for

h –b: upper bound for h. –c: variable h.

The drop of the steam temperature depicted by

this approach could lead to a suboptimal degree of

crosslinking especially near the core of the

insulation, where the heat diffusion is lower.

0 20 40 60 80 100 120

100

120

140

160

180

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 20 40 60 80 100 120

100

150

200

250

tube length [m]

Temperature [°C]

internal layer

middle layer

external layer

0 20 40 60 80 100 120

100

120

140

160

180

200

tube len

[

]

Temperature [°C]

internal layer

middle layer

external layer

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

0 0.5 1 1.5 2 2.5 3 3.5 4 4.5

distance from the external surface [mm]

% unreacted peroxide %

Experimental

Numerical

SIMULTECH2015-5thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

The optimal degree of crosslinking for a well-

defined compound could be achieved varying

mainly the following production parameters: (1) rate

of extrusion, (2) temperature of crosslinking, (3)

ratio between heating and cooling area.

Avoid the formation of parts where the steam

passes to liquid water.

In order to support and drive the plant manager

through such a difficult task, a numerical tool has

been developed and it is now available to be used to

set up industrial CV lines.

-a

-b

Figure 10: Test #1. Results obtained with h kept as

variable to optimize with the GA approach. –a: normalized

peroxide concentration along the thickness and the length

of the cable. –b: drop of

h along the length of the cable.

As it has been shown by the numerical

simulations provided in a companying paper (Milani

and Milani 2015), an accurate experimental

estimation of thermo-physical data (pressure and

temperature measures) of the steam provided point

by point along the pipe length is a key issue to

precisely predict the level of vulcanization of the

resulting cured item. When dealing with steam

vulcanization, indeed, it can occur that pressure

measures along the pipe are not strictly sufficient to

determine the steam temperature, because it could be

superheated. If this is the case, then the expression

for the relation between the temperature and

pressure for saturated vapor does not apply. This is

the reason why pressure measures should always be

coupled with temperature evaluations. If such a

monitoring system is at disposal to the producers,

Finite Elements can accurately predict the level of

vulcanization at the end of the production, without

the need to provide experimental a-posteriori DSC

analyses on selected samples. Conversely, the

monitoring system coupled with Finite Elements and

GA could be used to optimize the curing apparatus,

maximizing the output mechanical properties of the

insulator, especially in presence thick items.

REFERENCES

Haupt R. L., Haupt S. E., Practical Genetic Algorithms –

John Wiley and Sons

– 2004.

Kang S. L., Zong W. G.,

Computers and Structures, 82,

781 – 2004.

Kosar V., Gomzi Z., Thermochimica Acta, 457, 70 –

2007.

Lenir V. L., Polym. Eng. Sci., 24(9), 633 – 1984.

Milani G., Milani F.,

Journal of Computational Chemistry,

28 (13), 2203-2215– 2007.

Milani G., Milani F.,

Computers and Chemical

Engineering

, 32, 3198 – 2008.

Milani G., Milani F.,

Journal of Applied Polymer Science,

111(1), 482-507– 2009.

Milani G., Milani F., Journal of Mathematical Chemistry,

49(7), 1357-1383– 2011.

Milani G., Journal Math. Chem., 51(3), 1116 – 2013.

Milani G., Galanti A., Cardelli C., Milani F.,

Journal

Appl. Plym. Sci.,

131(8) 2014, paper #40075. DOI:

10.1002/app.40075.

Milani G., Milani F., Experimental/FEM optimization of

medium voltage rubber insulated electric cables

vulcanized with steam water. Differential Scanning

Calorimetry (DSC) and rheometer experimental

results. In Proc. 5

International Conference on

Simulation and Modeling Methodologies,

Technologies and Applications SIMULTECH2015,

Colmar, France, 21-23 July 2015.

0.7

0.8

0.9

100

0.2

0.4

0.6

0.8

Cooling

Length L [m]

Heating

Distance r [cm]

Normalized peroxide concentration

0 20 40 60 80 100 120

500

1000

1500

2000

2500

tube length [m]

h or h

[W/m

Experimental/FEMOptimizationofMediumVoltageRubberInsulatedElectricCablesVulcanizedwithSteamWater-

NumericalSimulationsandInverseAnalyses