
International Standard ISO 9001 an Artificial Intelligence View
José Neves
1
, Ana Fernandes
2
, Guida Gomes
1
, Mariana Neves
3
,
António Abelha
1
and Henrique Vicente
4
1
Algoritmi, Universidade do Minho, Braga, Portugal
2
Departamento de Química, Escola de Ciências e Tecnologia, Universidade de Évora, Évora, Portugal
3
Deloitte, Londres, U.K.
4
Departamento de Química, Centro de Química de Évora, Escola de Ciências e Tecnologia,
Universidade de Évora, Évora, Portugal
Keywords: International Standard ISO 9001, Knowledge Representation and Reasoning, Logic Programming, Artificial
Neural Networks.
Abstract: ISO 9001 is recognized as a Quality Management Systems standard, i.e., it is the primary phase of a process
of constant enhancement that will provide an organisation with the necessary management tools to improve
working practices. Indeed, it provides a framework and a set of principles aimed at ensuring a common
sense approach to the management of an organization in order to consistently satisfy customers and other
stakeholders. Therefore, and in order to add value to ISO 9001, this work focuses on the development of a
decision support system, which will allow companies to be able to meet the needs of customers by fulfilling
requirements that reflect either the effectiveness or the non-effectiveness of an organization. The procedures
for knowledge representation and reasoning used are based on an extension to the Logic Programming
language, allowing the handling of incomplete, contradictory and even forbidden data, information and/or
knowledge. The computational framework is centred on Artificial Neural Networks to evaluate customer’s
satisfaction and the degree of confidence that one has on such a happening.
1 INTRODUCTION
Organizations, either in the business sphere or in the
scope of the public sector, owe their existence to
their customer´s prospects in terms of commodities and
services and, the last but not the least, are also indebted
to reward their stakeholders. Quality Management
(QM) is one of the practices that can bring competitive
advantages to businesses, i.e., the implementation of
QM effectively influences enterprises performance
(Kaynak, 2003; Parast et al., 2011; Shahin and
Dabestani, 2011). Indeed, corporations that implement
QM aim to add value to their customers, i.e.,
improvement of processes and products quality leads
to reduce their costs and increase their profits
(Kaynak, 2003; Pignanelli and Csillag, 2008).
The ISO 9001 standard do not refers to the
compliance with a given goal or result. This standard
does not aim to measure the quality of the enterprises’
products or services but rather point out the need to
systematize a set of procedures and document such
implementation (Braun, 2005). The implementation of
ISO 9001 standard is voluntary, although in some
sectors it has become quasi-obligatory (Braun, 2005).
The International Standard ISO 9001 is applicable
to all sectors and organizations, regardless of their type,
size, product, or service. The standard is interpretative,
not prescriptive, offering an independent system of
managing and evaluation of companies’ performance,
allowing improving either their management practices
or their global recognition. ISO 9001 is based on 8
(eight) Quality Management Principles, which are
incorporated within the requirements of the standard,
and can be applied to develop organizational
performance (IPQ, 2008), in terms of:
• Customer focus;
• Leadership;
• Involvement of people;
• Process approach;
• System approach to management;
• Continual improvement;
• Factual approach to decision making; and
• Mutually beneficial supplier relationships.
421
Neves J., Fernandes A., Gomes G., Neves M., Abelha A. and Vicente H..
International Standard ISO 9001 an Artificial Intelligence View.
DOI: 10.5220/0005328904210428
In Proceedings of the 17th International Conference on Enterprise Information Systems (ICEIS-2015), pages 421-428
ISBN: 978-989-758-096-3
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

The derivative benefits are no less important, and
include:
• Enhanced reputation;
• Repeat business;
• Ability to compete more effectively globally,
both on quality and price;
• Access to new markets;
• Improved customer and supplier relationships;
• Improved employee morale; and
• Improved management control.
According to Tarí (Tarí, 2012) these benefits
may be catalogued into internal and external. The
former ones include improvements in corporate
processes, having positive effects on operational and
work forces issues (e.g. increase in productivity,
improvement in efficiency, reduction in costs,
training). The external benefits, in turn, relate to
effects on customers and society in general (e.g.
customer satisfaction, better relationships with
stakeholders, improved image).
This work reports the founding of a computational
framework that uses knowledge representation and
reasoning techniques to set the structure of the
information and the associate inference mechanisms.
We will centre on a Logic Programming (LP) based
approach to knowledge representation and reasoning
(Neves, 1984; Neves et al., 2007), complemented
with a computational framework based on Artificial
Neural Networks (Cortez et al., 2004, Caldeira et al.,
2011, Vicente et al., 2013). The requirements of ISO
9001 that can better predict the efficacy (or lack of
efficacy) of an organization were selected (IPQ,
2012). We take as example a company in the area of
training where two management indicators, namely
complaints and customer satisfaction were used and
attained by questionnaires. Both indicators consider
several items, namely Trainee´s General Information;
Trainee´s Complaints; Trainee´s Satisfaction; Quality
of Support Materials; and Inquiries of Trainee´s
Satisfaction, that will be described later.
2 KNOWLEDGE
REPRESENTATION AND
REASONING
Many approaches for knowledge representation and
reasoning have been proposed using the Logic
Programming (LP) paradigm, namely in the area of
Model Theory (Kakas et al., 1998; Gelfond and
Lifschitz, 1988; Pereira and Anh, 2009), and Proof
Theory (Neves, 1984; Neves et al., 2007). We
follow the proof theoretical approach and an
extension to the LP language, to knowledge
representations and reasoning. An Extended Logic
Program (ELP) is a finite set of clauses in the form:
←
,⋯,
,
,⋯,
(1)
?
,⋯,
,
,⋯,
,0
(2)
where “?” is a domain atom denoting falsity, the p
i
,
q
j
, and p are classical ground literals, i.e., either
positive atoms or atoms preceded by the classical
negation sign
(Neves, 1984). Under this
emblematic formalism, every program is associated
with a set of abducibles (Kakas et al., 1998; Pereira
and Anh, 2009) given here in the form of exceptions
to the extensions of the predicates that make the
program. Once again, LP emerged as an attractive
formalism for knowledge representation and
reasoning tasks, introducing an efficient search
mechanism for problem solving.
Due to the growing need to offer user support in
decision-making processes some studies have been
presented related to the qualitative models and
qualitative reasoning in Database Theory and in
Artificial Intelligence research (Halpern, 2005;
Kovalerchuck and Resconi, 2010). With respect to
the problem of knowledge representation and
reasoning in LP, a measure of the Quality-of-
Information (QoI) of such programs has been object
of some work with promising results (Lucas, 2003;
Machado et al., 2010). The QoI with respect to the
extension of a predicate i will be given by a truth-
-value in the interval [0,1], i.e., if the information is
known (positive) or false (negative) the QoI for the
extension of predicate
i
is 1. For situations where the
information is unknown, the QoI is given by:
→
1
0
≫0
(3)
where N denotes the cardinality of the set of terms or
clauses of the extension of predicate
i
that stand for
the incompleteness under consideration. For situations
where the extension of predicate
i
is unknown but
can be taken from a set of values, the QoI is given by:
1
(4)
where Card denotes the cardinality of the abducibles
set for i, if the abducibles set is disjoint. If the
abducibles set is not disjoint, the QoI is given by:
1
⋯
(5)
where
is a card-combination subset, with Card
elements. The next element of the model to be
considered is the relative importance that a predicate
assigns to each of its attributes under observation,
i.e.,
, which stands for the relevance of attribute k
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
422

in the extension of
. It is also assumed that
the weights of all the attribute predicates are
normalized, i.e.:
1,∀
(6)
where
denotes the universal quantifier. It is now
possible to define a predicate’s scoring function
so that, for a value
,⋯,
, defined in
terms of the attributes of
, one may have:
⁄
(7)
allowing one to set:
,⋯,
∷
(8)
It is now possible to engender the universe of
discourse, according to the information given in the
logic programs that endorse the information about
the problem under consideration, according to
productions of the type:
,⋯,
∷
∷
(9)
where
⋃
and m stand, respectively, for “set union” and
the cardinality of the extension of predicate
i
. On the
other hand, DoC
i
denotes one’s confidence on the
attribute`s values of a particular term of the
extension of predicate
i
, whose evaluation will be
illustrated below. In order to advance with a broad-
spectrum, let us suppose that the Universe of Discourse
is described by the extension of the predicates:
⋯
,
⋯
,⋯,
⋯
0
(10)
Assuming we have a clause that is mapped into a
case, that clause has as argument all the attributes
that make the case. The argument values may be of
the type unknown or members of a set, may be in the
scope of a given interval or may qualify a particular
observation. Let us consider the following clause
where the second argument value may fit into the
interval [3,5] with a domain of [0,8], the value of the
third argument is unknown, which is represented by
the symbol
, with a domain that ranges in the
interval [5,15], and the first argument stands for
itself, with a domain that ranges in the interval [0,3].
Let us consider that the case data is given by the
extension of predicate
, given in the form:
:
,
,
→,
(11)
where “{” and “}” is one´s notation for sets, where
“0” and “1” denote, respectively, the truth values
“false” and “true”. One may have:
,
,
⟵
,
,
2,
3,5
,
`
∷1∷
0,3
0,8
5,15
`
Once the clauses or terms of the extension of the
predicate are established, the next step is to
transform all the arguments, of each clause, into
continuous intervals. In this phase, it is essential to
consider the domain of the arguments. As the third
argument is unknown, its interval will cover all the
possibilities of the domain. The first argument speaks
for itself. Therefore, one may have:
,
,
⟵
,
,
2,2
,
3,5
,
5,15
`
∷1∷
0,3
0,8
5,15
`
Now, one is in position to calculate the Degree of
Confidence for each attribute that makes the term´s
arguments (e.g. for attribute two it denotes one’s
confidence that the attribute under consideration fits
into the interval [3,5]). Next, we set the boundaries of
the arguments intervals to be fitted in the interval [0,1]
according to the normalization procedure given in
the procedural form by
/
,
where the
stand for themselves.
,
,
⟵
,
,
20
30
,
20
30
,
30
80
,
50
80
,
55
155
,
155
155
0.67,0.67
,
0.38,0.62
,
0,1
`
∷1∷
0,1
0,1
0,1
`
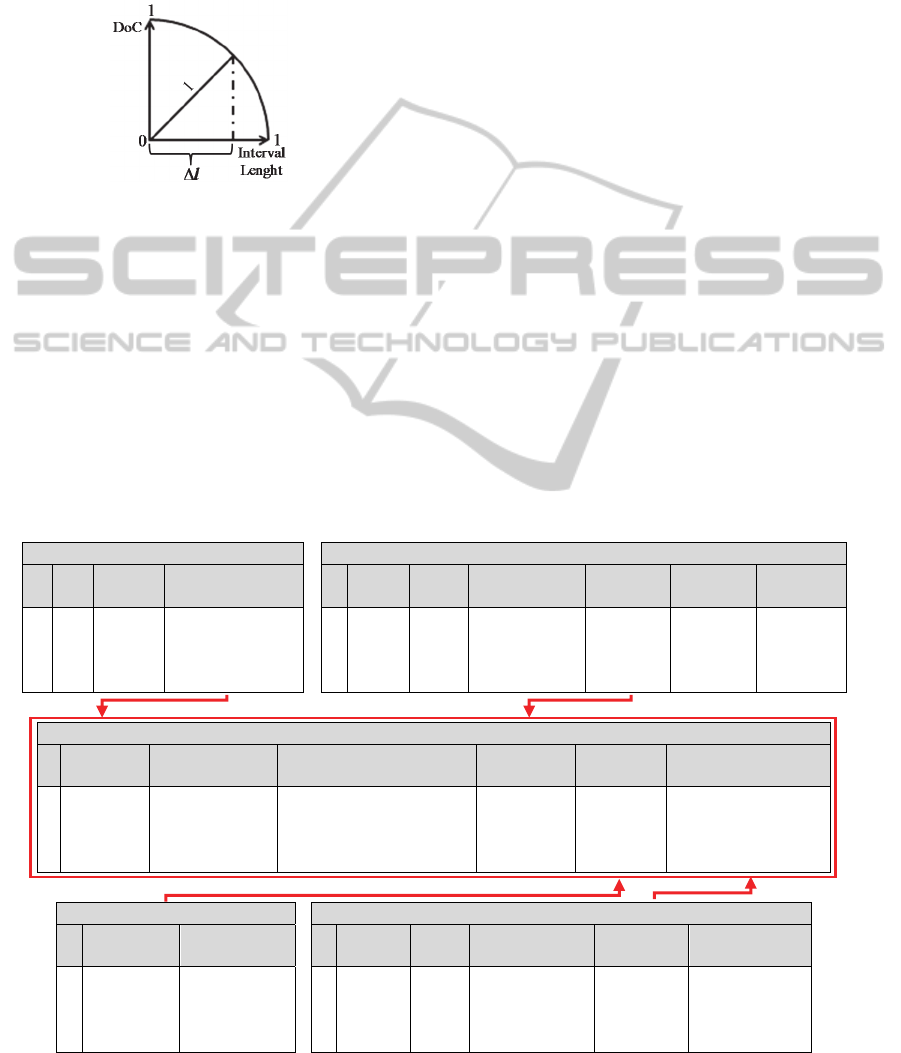
The Degree of Confidence (DoC) is evaluated using
the equation
√
1∆
, as it is illustrated in
Figure 1, where ∆ stands for the length of the
argument´s intervals, once normalized.
,
,
⟵
,
,
1,0.968,0
`
∷1∷0.656
0.67,0.67
0.38,0.62
0,1
`
InternationalStandardISO9001anArtificialIntelligenceView
423
0,1
0,1
0,1
`
where the DoC’s for f
1
(1, 0.968, 0) is evaluated as
(1+0.968+0)/3 = 0.656, assuming that all the
argument’s attributes have the same weight.
Figure 1: Computing the Degree of Confidence values.
3 A CASE STUDY
In order to exemplify the applicability of our ideal,
we will look at the relational database model, since
it provides a basic framework that fits into our
expectations (Liu and Sun, 2007), and is understood
as the genesis of the LP approach to Knowledge
Representation and Reasoning (Neves, 1984).
As a case study, consider the scenario where a
relational database is given in terms of the extensions
of the relations depicted in Figure 2, which stands for
a situation where one has to manage information
about trainees’ satisfaction evaluation. Under this
scenario some incomplete and/or default data is also
available. For instance, in the Trainees’ Satisfaction
database, the opinion of trainee 1 about Support
Materials is unknown, while the Inquiries of
Trainees’ Satisfaction ranges in the interval [16, 21].
In Trainees’ Complaints database, 0 (zero) denotes
absence and 1 (one) denotes existence of complaints.
The issues of Quality of Support Materials and
Inquiries of Trainees’ Satisfaction databases range
in the interval [0, 5], i.e., range between Inadequate
(0) and Excellent (1). In Trainee Situation Column
of the Trainees’ Satisfaction database 0, 1 and 2
stands respectively for dropped out, ongoing and
course finished. The values presented in General
Opinion about the Course and Willingness to
Recommend the Company columns ranges in the
interval [0, 10]. In the former case 0 (zero) stands
for Strongly Negative Opinion and 10 (ten) denotes a
Strongly Positive Opinion. In the last case 0 (zero)
stands for None and 10 (ten) denotes Absolutely
Sure. The values presented in the remaining columns
are the sum of the respective databases, ranging
between [0, 6], [0, 10] and [0, 25] respectively for
Complaints, Support Materials and Inquiries of
Trainees’ Satisfaction columns.
Now, we may consider the relations given in
Figure 2, in terms of the satisfaction predicate, given
in the form:
Trainees’ General Information
Trainees’ Complaints
# Age Gender Trainee Situation # Billing Trainer Infrastructures
Customer
Service
Sale
Arguments
Support
Materials
1 27 Female finished 1 0 0 0 0 0 0
2 32 Male dropped out 2 1 1 1 0 1 1
n 21 Female ongoing n 1 0 1 0
0
0
Trainees’ Satisfaction
#
Trainee
Situation
General Opinion
about the Course
Willingness to
Recommend the Company
Complaints
Support
Materials
Inquiries of Trainees'
Satisfaction
1 2 9 8 0
[16,21]
2 0 3 2 5 4 12
n 1 [8,9]
2 8 22
Quality of Support Materials
Inquiries of Trainees’ Satisfaction
# Syllabus Materials # Guidance Trainer
Image of the
Training Course
Customer
Service
Methodologies
1
1 4 4
4 4
2 2 2 2 2 2 3 3 2
n 4 4 n 5 5 3 4 5
Figure 2: Extension of the Relational Database model.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
424

:
,
,
,
,
,
→0,1
where 0 (zero) and 1 (one) denote, respectively, the
truth values false and true. It is now possible to give
the extension of the predicate satisfaction, in the
form:
{
,,,,,
←
,,,,,
2,9,8,0,,16,21
`
∷1∷
0,2
0,10
0,10
0,6
0,10
0,25
`
}
In this program, the first clause denotes the closure
of predicate satisfaction. The next clause
corresponds to the trainee 1, taken from the
extension of the satisfaction relation presents in
Figure 2. Moving on, the next step is to transform
all the argument values into continuous intervals and
then normalize the predicate´s arguments in order to
obtain the Degree of Confidence of the satisfaction
predicate. One may have:
{
,,,,,
←
,,,,,
2,2
,
9,9
,
8,8
,
0,0
,
0,10
,16,21
`
∷1∷
0,2
0,10
0,10
0,6
0,10
0,25
`
}
The logic program referred to above, is now presented in the form:
{
,,,,,
←
,,,,,
1,1,1,1,0,0.98
`
∷1∷0.83
1,1
0.9,0.9
0.8,0.8
0,0
0,1
0.64,0.84
`
0,1
0,1
0,1
0,1
0,1
0,1
`
}
where its terms make the training and test sets of the
Artificial Neural Network given in Figure 3.
4 ARTIFICIAL NEURAL
NETWORKS
Several studies have shown how Artificial Neural
Networks (ANNs) could be successfully used to
model data and capture complex relationships
between inputs and outputs (Caldeira et al., 2011,
Vicente et al., 2013, Salvador et al., 2013). ANNs
simulate the structure of the human brain being
populated by multiple layers of neurons. As an
example, let us consider the last case presented in
Figure 2, where one may have a situation in which
information about trainees’ satisfaction is needed,
given in the form:
{
,,,,,
←
,,,,,
1,
8,9
,,2,8,22
`
∷1∷
InternationalStandardISO9001anArtificialIntelligenceView
425

0,2
0,10
0,10
0,6
0,10
0,25
`
,,,,,
←
,,,,,
1,1
,
8,9
,
0,10
,
2,2
,
8,8
,22,22
`
∷1∷
0,2
0,10
0,10
0,6
0,10
0,25
`
,,,,,
←
,,,,,
0.5,0.5
,
0.8,0.9
,
0,1
,
0.33,0.33
,
0.8,0.8
,0.88,0.88
`
∷1∷
0,1
0,1
0,1
0,1
0,1
0,1
`
,,,,,
←
,,,,,
1,0.995,0,1,1,1
`
∷1∷0.833
0.5,0.5
0.8,0.9
0,1
0.33,0.33
0.8,0.8
0.88,0.88
`
0,1
0,1
0,1
0,1
0,1
0,1
`
}
In Figure 3 it is shown how the normalized values of
the interval boundaries and their DoC and QoI
values work as inputs to the ANN. The output
translates the trainees’ satisfaction and the confidence
that one has on such a happening. In addition, it also
contributes to build a database of study cases that
may be used to train and test the ANNs.
In this study 200 samples (i.e. two hundred terms
or clauses of the extension of predicate) were
considered, coming from a vocational training
company of the Lisbon region. The trainees’ age
average was 25.4 years, ranging from 17 to 32 years
old. The gender distribution was 48.3% and 51.7%
for male and female, respectively. Regarding
trainees’ situation, 28.4% completed their training,
12.3% dropped out and 59.3% are attending training.
The dataset used in the training phase it was
divided in exclusive subsets through the 10-folds
cross validation. In the implementation of the
respective dividing procedures, ten executions were
performed for each one of them. To ensure statistical
significance of the attained results, 30 (thirty)
experiments were applied in all tests. The back
propagation algorithm was used in the learning
process of the ANN. As the output function in the
pre-processing layer it was used the identity one. In
the other layers we used the sigmoid function.
A common tool to evaluate the results presented
by the classification models is the coincidence
matrix, a matrix of size L × L, where L denotes the
number of possible classes (2 (two) in the present
case). Table 1 present the coincidence matrix (the
values denote the average of the 30 experiments). A
perusal of Table 1 shows that the model accuracy
was 95.5% (191 instances correctly classified in
200).
Table 1: The coincidence matrix for the ANN model.
Target
Predict
False (0) True (1)
False (0) 48 4
True (1) 5 143
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
426

Figure 3: The Artificial Neural Network topology.
5 CONCLUSIONS AND FUTURE
WORK
This customer satisfaction assessment system is able
to give an adequate response to the need for a good
method of customer satisfaction prediction. To go
around the problem, more effectively, much more
variables must be studied and considered, thus
fulfilling important gaps in the existent satisfaction
assessment methods.
Being an area filled with incomplete and
unknown data it may be tackled by Artificial
Intelligence based methodologies and techniques to
problem solving. This work presents the founding of
a computational framework that uses powerful
knowledge representation and reasoning techniques
to set the structure of the information and the
associate inference mechanisms. Indeed, this method
brings a new approach that can revolutionize
prediction tools in all its variants, making it more
complete than the existing methodologies and tools
available.
The knowledge representation and reasoning
techniques presented above are very versatile and
capable of covering every possible instance by
considering incomplete, contradictory, and even
unknown data. Indeed, the new paradigm of
knowledge representation and reasoning enables the
use of the normalized values of the interval
boundaries and their DoC values, as inputs to the
ANN. The output translates the customer satisfaction
prediction and the confidence that one has on such a
happening.
Future work may recommend that the same
problem must be approached using others
computational frameworks like Case Based
Reasoning (Carneiro et al., 2013), Genetic
Programming (Neves et al., 2007), or Particle
Swarm (Mendes et al., 2004), just to name a few.
ACKNOWLEDGEMENTS
This work has been supported by FCT – Fundação
para a Ciência e Tecnologia within the Project Scope
UID/CEC/00319/2013.
REFERENCES
Braun, B., 2005. Building global institutions: the diffusion
of management standards in the world economy – an
institutional perspective. In C. Alvstam, E. Schamp
Eds, Linking Industries Across the World, Ashgate.
London, 3-27.
Caldeira, A.T., Arteiro, J., Roseiro, J. Neves, J., Vicente, H.,
2011. An Artificial Intelligence Approach to Bacillus
amyloliquefaciens CCMI 1051 Cultures: Application
to the Production of Antifungal Compounds.
Bioresource Technology, 102: 1496-1502.
Carneiro, D., Novais, P., Andrade, F., Zeleznikow, J.,
Neves, J., 2013. Using Case-Based Reasoning and
Principled Negotiation to provide decision support for
dispute resolution. Knowledge and Information Systems,
36: 789-826.
Cortez, P., Rocha, M., Neves, J., 2004. Evolving Time Series
Forecasting ARMA Models. Journal of Heuristics, 10:
415-429.
Gelfond, M., Lifschitz, V., 1988. The stable model
semantics for logic programming. In Logic
Programming – Proceedings of the Fifth International
Conference and Symposium, 1070-1080.
Halpern, J., 2005. Reasoning about uncertainty. MIT
Press. Massachusetts.
IPQ, 2008. NP EN ISO 9001:2008 – Quality Management
Systems – Requirements, Portuguese Institute of
Quality Edition. Caparica, 3
rd
edition (in Portuguese).
IPQ, 2012. NP 4512:2012 – Vocational Training
Management System, Including Technology Enhanced
Learning – Requirements, Portuguese Institute of
Quality Edition. Caparica (in Portuguese).
Kakas A., Kowalski R., Toni F., 1998. The role of
abduction in logic programming. In Handbook of
Pre-processing
Layer
Input
Layer
Hidden
Layer
Output
Layer
1
1
1
GO
1
1
0
0
SM
1
0.84
0.64
0.98
ITS
1
BiasBias
0.83
DoC
0
costumer
satisfaction
•
•
•
•
•
•
•
•
•
InternationalStandardISO9001anArtificialIntelligenceView
427

Logic in Artificial Intelligence and Logic
Programming, Volume 5, 235-324.
Kaynak, H., 2003. The relationship between total quality
management practices and their effects on firm perform-
ance. Journal of Operations Management, 21: 405-435.
Kovalerchuck B., Resconi G., 2010. Agent-based uncertainty
logic network. In Proceedings of the IEEE International
Conference on Fuzzy Systems – FUZZ-IEEE, 596-603.
Liu, Y., Sun, M., 2007. Fuzzy optimization BP neural
network model for pavement performance assessment.
In 2007 IEEE international conference on grey systems
and intelligent services, Nanjing, China, 18-20.
Lucas, P., 2003. Quality checking of medical guidelines
through logical abduction. In Proceedings of AI-2003,
Springer. London, 309-321.
Machado, J., Abelha, A., Novais, P., Neves, J., 2010.
Quality of service in healthcare units. International
Journal of Computer Aided Engineering and
Technology, 2: 436-449.
Mendes, R., Kennedy, J., Neves, J., 2004. The Fully Informed
Particle Swarm: Simpler, Maybe Better. IEEE Trans-
actions on Evolutionary Computation, 8: 204-210.
Neves, J., 1984. A logic interpreter to handle time and
negation in logic data bases. In Proceedings of the
1984 annual conference of the ACM on the fifth
generation challenge, 50-54.
Neves, J., Machado, J., Analide, C., Abelha A., Brito L.,
2007. The halt condition in genetic programming. In
Progress in Artificial Intelligence – Lecture Notes in
Computer Science, Volume 4874, Springer. Berlin,
160-169.
Parast, M., Adams, S., Jones, E., 2011. Improving Operation-
al and Business Performance in the Petroleum Industry
through Quality Management. International Journal of
Quality & Reliability Management, 28: 426-450.
Pereira L., Anh H., 2009. Evolution prospection. In New
Advances in Intelligent Decision Technologies – Results
of the First KES International Symposium IDT, 51-64.
Pignanelli, A., Csillag, J., 2008. The Impact of Quality
Management on Profitability: An Empirical Study.
Journal of Operations and Supply Chain Management
1: 66-77.
Salvador, C., Martins, M. R., Vicente, H., Neves, J.,
Arteiro J., Caldeira, A.T., 2013. Modelling Molecular
and Inorganic Data of Amanita ponderosa Mushrooms
using Artificial Neural Networks. Agroforestry Systems,
87: 295-302.
Shahin, A., Dabestani, R., 2011. A feasibility study of the
implementation of total quality management based on
soft factor. Journal of Industrial Engineering and
Management, 4: 258-280.
Tarí, J., Azorín, J., Heras, I., 2012. Benefits of the ISO 9001
and ISO 14001 standards: A literature review. Journal of
Industrial Engineering and Management, 5: 297-322.
Vicente, H., Dias, S., Fernandes, A., Abelha, A.,
Machado, J., Neves, J., 2012. Prediction of the Quality
of Public Water Supply using Artificial Neural
Networks. Journal of Water Supply: Research and
Technology – AQUA, 61: 446-459.
ICEIS2015-17thInternationalConferenceonEnterpriseInformationSystems
428
