Spatiotemporal Complex Geometrical Optics (CGO) of N 3D

Interacting Asymmetric Gaussian Wave Packets in Nonlinear

Medium

CGO as the Simplest and Efficient Method for Spatiotemporal Evolution

Pawel Berczynski

and Slawomir Marczynski

Institute of Physics, West Pomeranian University of Technology, Piastow 48, Szczecin 70-310, Poland

Faculty of Mechanical Engineering and Mechatronics, West Pomeranian University of Technology,

Piastow 48, Szczecin 70-310, Poland

Keywords: Spatiotemporal Complex Geometrical Optics, Asymmetric 3D Wave Packets, Spatiotemporal Evolution in

Nonlinear Medium, Interaction of N 3D Gaussian Wave Packets in Nonlinear Medium, Kerr Type Medium.

Abstract: The complex geometrical optics (CGO) was applied for the spatiotemporal evolution of arbitrary number of

3D mutually incoherent (with different carrier frequencies) Gaussian wave packets (GWPs) interacting and

propagating in a nonlinear medium of Kerr type. The CGO reduced description of the propagation of the

beam, the pulse and the wave packet to complex ordinary differential equations (ODE) This leads to

exceptionally fast numerical algorithms. We observed high efficiency of the CGO method to compute

interactions of arbitrary number of 3D Gaussian wave packets propagating in a nonlinear (anomalous)

dispersive medium of the Kerr type. The derived CGO equations were compared with equations obtained by

the variational method. CGO described the Gaussian beam propagation in free space as well as the Gaussian

pulse spreading in the linear anomalous dispersive medium more illustratively than both the Fourier transform

method and the Fresnel diffraction integral method. The spatiotemporal CGO has been proven to be a method

more practical than the spectral analysis, the variational method, the method of moments and the method of

the generalized eikonal approximation. Complementary to the presented results, an on-line CGO solver,

implemented in Javascript, is freely available at the authors’ website: http://slawek.ps.pl/odelia.html.

1 INTRODUCTION

In traditional understanding, the geometrical optics

(GO) is the method to create pictures based on

geometrical evolutions of light rays. However, in a

wider recognition GO can be classified to be an

approximated method to describe the wave motion of

wave fields such as beams, pulses and wave packets.

Such wider recognition was first established by

papers and books of Debye, Sommerfeld, Runge and

Luneburg (Sommerfeld, 1964; Luneburg, 1964;

Kline and Kay, 1965; Born and Wolf, 1959), who

proposed the geometrical form of the wave field

representation and who derived from the wave

equation two geometrical optics equations: the

transport equation describing the amplitude and the

eikonal equations, which determine the phase of the

signal. Operation of the first laser in 1960 emphasized

the importance of concepts of Sommerfeld, Runge,

Born, Wolf and Luneburg to describe the evolution of

the laser fundamental mode in the form of Gaussian

beam (GB). At the beginning of the 1960’s, Kravtsov

proposed the method of geometrical optics based on

the concepts of complex rays (Kravtsov, 1967), the

bundle of which can represent the Gaussian wave

field (Deschamps, 1971) and which enables to

include the effect of a spatially limited beam

diffraction in the free space into the scope of the

classical geometrical ray description.

Contemporaneously, Kogelnik (Kogelnik, 1965)

proposed the representation of a collimated beam by

introduction of the quasi-optical complex parameter

1/q, which describes the evolution of two beam

parameters: the GB width and the radius of the

curvature in the one single complex quantity, which

can be transformed through lens-like media,

including resonators and even more advanced optical

systems. Nowadays, the Kogelnik transformation

laws are expressed in a more general convenient form

Berczynski P. and Marczynski S..

Spatiotemporal Complex Geometrical Optics (CGO) of N 3D Interacting Asymmetric Gaussian Wave Packets in Nonlinear Medium - CGO as the

Simplest and Efﬁcient Method for Spatiotemporal Evolution.

DOI: 10.5220/0005291600530060

In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 53-60

ISBN: 978-989-758-092-5

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

referred to as the ABCD matrix method, or the the

generalized beam matrix method (for instance

generalized to ABCDGH matrix). Another quasi-

optical method is the nonlinear geometrical optics

(NGO) proposed by (Akhmanov, Sukhorukov and

Khokhlov, 1968), which uses the parabolic equation

to describe self-focusing of a GB in a nonlinear

medium of Kerr type. Nowadays, the NGO formalism

is often recognized as a generalized eikonal

approximation (Yap, Quek and Low, 1998), which

was used at the end of the 1990’s to describe the

propagation of stationary electromagnetic waves in

linear and nonlinear media and the evolution of

electromagnetic pulse in a linear dispersive medium.

During the 1960’s/70’s, at least four other methods

were proposed to describe optical beams: the dynamic

ray tracing (Luneburg, 1964; Deschamps and Mast,

1964; Arnaud 1976), which describes geometrical

spreading of the rays using Hamilton equations; the

method of inhomogeneous wave tracking

(Choudhary and Felsen, 1974; Felsen, 1976), which

bases on some specific regularities concerning

evolution of the family of phase paths and wave

fronts. Finally, evolution of the phase paths and wave

fronts enables to construct the wave field of the beam;

the method of moments (MM) (Vlasov, Petrischev

and Talanov, 1971), which deals with intensity

moments satisfying the parabolic equation and

allowing to determine the power of the wave beam,

the centre of the beam intensity, the beam divergence

and the evolution of the effective beam radius; the

variational method (Anderson, 1983), called also the

Ritz method, which bases on semi-analytical

approach to the pulse and the beam propagation by

means of the standard variational principle. In 2004,

the CGO method dealing with the complex eikonal

and the complex amplitude was proposed to describe

the first GB diffraction in homogeneous and

inhomogeneous media (Berczynski and Kravtsov,

2004). The CGO method enables to reduce

immediately the complicated spatial and temporal

description based on partial differential equations to

solving ordinary differential equations contrary to

other methods detailed above. The CGO method was

next applied to describe the self-focusing of GBs in

nonlinear inhomogeneous fibres (Berczynski, 2011)

and in nonlinear saturable media with absorption

(Berczynski, 2013). First of all, we demonstrate in

this paper that CGO method enables to perform fast

and effective numerical calculations based on ODEs.

In this way, the complexity and problems related to

nonlinear optics can be solved and analysed in more

illustrative and transparent way.

2 FIRST-ORDER COMPLEX

EQUATIONS OF CGO

METHOD

CGO method deals with eikonal equation, which, for

spatiotemporal evolution of a 3D wave packet in a

medium with relative permittivity

and anomalous

dispersion, can be presented in a convenient form

ψψ













′

∂

′

∂













′

∂

′

∂













′

∂

′

∂













′

∂

′

∂

(1)

In Eq. (1)

()

ωω

kkzkt

′′′

−=

′

denotes scaled time,

ηη

′

202

′

are dimensionless transverse

coordinates,

zkz

′

denotes dimensionless

propagation direction and

′

is dimensionless

eikonal, where

(

is the wavelength in

vacuum). Within the spatiotemporal CGO method,

eikonal

′

is complex-valued and takes the form

()

3,2,1,2/

′′

′



izBz

(2)

)(zBB

= denotes complex functions with

introduced convenient notation including temporal

coordinate

τη

′

. The real parts of

B embrace

spatial and temporal chirps

whereas imaginary

parts include widths

w . Thus, the form of the

complex parameters

)(zBB

= is as follows:

iiIiRii

wiiBBB +=+=

(3)

Expanding subsequently relative permittivity

()

′′′′

= ,,,

z in Eq. (1) in Taylor series in

′′′

and substituting Eq. (3) into Eq. (1) we

obtain first-order Riccati type equations in the form

′

(4)

000

3000

2,1

2121

|||

,|||

′

∂

′

∂

ηηττηη

(5)

Equations in Eq. (4) can expressed by real and

imaginary parts of

B in the form











′

=−+

′

IiRi

iIiRi

(6)

The above equations in Eq. (6) lead to the known

relations between the packet widths

w and chirps

together with ordinary differential equation:

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

=−

′

ακ

(7)

Transport equation:

0)(

′

∇

Adiv

(8)

for CGO representation of eikonal in Eq. (2) together

with paraxial approximation leads immediately to a

first-order ordinary differential equation for complex

amplitude in the form













′



(9)

By integrating the above equation, we obtain the

complex amplitude of Gaussian wave packet in the

form

()













′













−=

′





zdzBAzA

)(

exp

(10)

where

()

AA = is the initial amplitude. The

modulus of complex amplitude has the form

() ()













′













−=

′





zdzBAzA

)(

exp

(11)

where

iRi

BB Re=

. The first integral of the second

equation in Eq. (6) leads to the dependences

(

)



′

−= zdBBB

RiIiIi

2exp)0(/

(12)

Using Eq. (3), we obtain spatiotemporal energy flux

conservation principle

0030201

321

AwwwAwww =

(13)

3 CGO, GEA, FOURIER

TRANSFORM, FRESNEL

DIFFRACTION INTEGRAL.

COMPARATIVE ANALYSIS

For the readers’ convenience, let us now compare the

efficiency of the CGO method with GEA formalism

on the example of a quite fundamental evolution of

wave packet in a linear dispersive medium. The two

methods mentioned above are based on the analogous

starting equations but CGO method which uses

complex quantities (eikonal and amplitude) reduces

automatically the description based on partial

differential equations to solving ordinary differential

equations for the packet parameters, which is

demonstrated below.

Following (Yap, Quek and Low, 1998), let us define

first using GEA approach real valued phase

and

real valued envelope

of the optical signal. The

fundamental disadvantage of the GEA approach lies

in the fact that both the amplitude and the phase

depend on all spatial and temporal parameters (

, z), which leads to coupled partial differential

equations (generalized eikonal equation and transport

equation), which require a lot of efforts to be solved.

GEA utilizes a representation of the wave packet in

the form

() ( ) ( )

),(exp,,

rrr Liktu =

(14)

where

zyx

zyx eeer ++=

. Substituting Eq. 14 into the

wave equation [Born and Wolf, 1959], the set of

partial differential equations is obtained in the

complicated form

()

ωω

∂

′′

−∇+=













∂

′′

−∇ kk

kkL

(15)

0)(

∂

′′

−

∂

′′

−∇⋅∇

ττ

ωω

kkL

(16)

It is notable that the above equations are always

coupled even in the simplest case of a homogeneous

medium, where relative permittivity

is constant.

Finally, in the paper (Yap, Quek and Low, 1998) we

notice the need to apply difficult mathematical

formalism of Hamilton optics to solve the above

equations to obtain the well known formulas for GB

propagation in free space and Gaussian pulse

evolution in linear dispersive medium. Let us now

explain, why the CGO method has an advantage over

GEA and enables essential simplification of the

starting equations (eikonal equation in standard form

and transport equation) to solve quickly ordinary

differential equations. First of all, this CGO

simplifications is possible only when we introduce

complex amplitude A and complex eikonal

instead

of real envelope

and real phase

used within

GEA approach. It can be noticed that complex form

of any parameter, which includes “space” for both

real and imaginary parts let us “pack” more

information in formally the same quantity. Moreover,

this obvious conclusion enables us in some sense to

control the dependence of pair of complex functions

on spatial and temporal parameters z,

. As

it is presented below, this complex generalization

enables us to simplify mathematical description

substantially. Furthermore, this complex

generalization leads to the same results as obtained by

GEA. It is noteworthy that Eq. (14) describing a 3D

Gaussian wave packet can be presented in the form

SpatiotemporalComplexGeometricalOptics(CGO)ofN3DInteractingAsymmetricGaussianWavePacketsinNonlinear

Medium-CGOastheSimplestandEfficientMethodforSpatiotemporalEvolution

()

() ()

























′

+⋅

⋅













′

−=



/2/exp

2/exp

kzzzik

zwu

ϕηκ

ηφ

(17)

() ()













′

−=



2/exp,

ηφτφ

(18)

=),(

() ()



′

/2/

kzzz

ϕηκ

(19)

Next, let us present the same wave field to separate

two functions: one depending only on propagation

distance z and the second including all the possible

longitudinal and transverse coordinates with time.

Thus, we have

()

























′

+⋅

⋅=



2/2/exp

)(exp

iiii

wizik

ziu

ηηκ

(20)

This way, Eq. (20) let us define complex amplitude,

which depends only on propagation distance z

()

)(exp)(

zizAA

(21)

and complex eikonal

(,, ,z

ψψ

τη η

) =

222

/2 /2

ii i i

ziw

κη η

′′



(22)

which depends on all possible spatial and temporal

parameters . The dependence in the form

)(zAA =

can be justified by geometrical optics assumption in

which the wave packet should be localized (paraxial)

in the vicinity of propagation direction z. But,

complex eikonal

),,,(

in Eq. (22)

receives more general interpretation, where the

constant real part of eikonal



′

ηκ

describes evolution of wave fronts in space and time,

whereas imaginary part



′

represents

evolution of phase-paths described by spatiotemporal

rays normal to wave fronts, determining finally the

power flow direction in space and time. Thus, CGO

representation of spatiotemporal wave object has the

form

() () ()()

,exp,

rr ikzAu =

(23)

When we substitute CGO representation in Eq. (23)

into wave equation [Born and Wolf, 1959] we obtain

a set of two equations of geometrical optics:

()

0)(,

=∇=∇

ψεψ

Adiv

(24)

which are never coupled in a linear medium. In Eq.

(24) the differential operator

∇

is 4-vector which

lades to spatiotemporal eikonal equation in the form

ψψ













∂

′′

−













∂













∂













∂

(25)

The complex eikonal equation in Eq. (25) for the case

of anomalous dispersion of group velocity

′′

and

after performing scaling procedures (discussed at the

beginning of Sec. 1) can be transformed into the

eikonal equation in dimensionless form presented in

Eq. (1). In this way CGO method uses eikonal

equation in the standard form [Born and Wolf, 1959]

and does not to require to the generalized eikonal to

be defined as opposed to GEA approach. Moreover,

it is notable that when the complex amplitude of 3D

wave packet depends only on the propagation

distance

)(zAA = a number of terms containing

transverse derivatives

∂∂A ,

∂∂A and

∂∂ /A

automatically vanishes in the transport equation. This

fact allow us to reduce immediately the partial

differential in Eq. (8) to solving the ordinary

differential equation in Eq. (9) taking into account

paraxial approximation to describe the localized wave

packet in CGO language. For comparative analysis,

let us apply now the CGO method to describe a 3D

wave packet evolution in a linear (anomalous)

dispersive medium. Thus, following CGO procedure

we reduce immediately the eikonal equation to

solving a first-order differential equation, which for

the case of a homogeneous medium has the form

3,2,1

,0 ==+

′

(26)

The solution of Eq. (26) has the form

′

)0(1

)0(

)(

(27)

For the packet with zero initial chirps and initial

spatial widths

)0(

, the initial value of complex

CGO parameter

has the form

)0(/)0(/)0()0(

iiii

wiwiB =+=

. Including this initial

condition we obtain solution for

)(zBB

in the

form

ziw

wzi

′

)0()0(/1

)0(/

)(

(28)

The real and imaginary parts of the above solution are

equal to

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

() ()

)0(

)(Im,

)(Re

′

(29)

As a result, the spatial packet widths and spatial

packet chirps turn out to be

()

,10

′













′

(30)

where

)0(

iDi

wL =

′

denotes dimensionless diffraction

distance for dimensionless spatial packet widths

)0(

and

)0(

. We would like to emphasize that the

solutions in Eq. (30) are identical with that obtain

using Fresnel diffraction integral (Berczynski,

Marczynski, 2014). CGO solutions for temporal

width and chirp have the form

()

,10

′













′

κσσ

(31)

where

)0(/)0(

′′

′

kTkL

denotes dimensionless

dispersion distance for dimensionless temporal width

of the packet

)0(

. It is worth emphasizing that the

solutions in Eq. (31) are also identical with results

obtained using Fourier transform for Gaussian pulses,

when the initial temporal chirp is zero (Sauter, 1996).

To compare solutions obtained by CGO and Fourier

transform for Gaussian pulse propagating in linear

(anomalous) dispersion medium, let us point that the

zero initial chirp expressed by the initial condition

)0(/)0(

wiB =

mentioned above is equivalent to the

condition

in the book by (Sauter, 1996).

However, solutions in Eq. (9.25) (Sauter, 1996) for

tΔ (FWHM) and

should be modified a little to be

compared with CGO solutions in Eq. (31), taking into

account the slightly different definitions of

a in Eq.

(9.1) in the form

(

)

exp),0(

taEtzE −==

as compared

with CGO definitions of the width in Eqs. (2,3),

where

(

)

(

)

222

2exp2exp

στη

−=−= AwAu

. Thus, to

compare results using the two methods mentioned

above, the Eq. (25) presented by (Sauter, 1996)

should be converted using substitution:

/14

Summarizing this comparable analysis, it can be

stated that the CGO method gives us the same

solutions as Fourier transform and Fresnel diffraction

integral when we describe a 3D wave packet

propagating in a linear dispersive (anomalous)

medium. However, it can be observed that

replacement of Fourier transform and Fresnel

diffraction integral by CGO method means that

integrating transform procedures in space and time

are substituted by first order complex differential

equation shown in Eq. (26), which embraces both

spatial and temporal effects. This way, we have

proven that the CGO method essentially simplifies

the description of wave motion of beams, pulses and

wave packets as compared with generalized eikonal

approximation method and as compared with

classical integral spectral methods, yielding identical

solutions.

4 INTERACTION AND

EVOLUTION OF ARBITRARY

NUMBER OF 3D GAUSSIAN

WAVE PACKETS IN

NONLINEAR MEDIUM

Let us now generalize CGO method to describe an

arbitrary number N of 3D wave packets propagating

in a nonlinear medium of Kerr type. Thus, the single

Eq. (1) takes a form on N coupled eikonal equations

()

iiii

uuu

,,,,



ωε

ψψ













′

∂

′

∂













′

∂

′

∂













′

∂

′

∂













′

∂

′

∂

(32)

with N permittivities depending on each of carrier

frequencies of

N 3D wave packets in the form

()

(

)

11021

,,,,

NiNiiiNi

uuuuuu

εεεεωε

++++= 

(33)

The single transport equation in Eq. (8) takes a form

of N equations

()













′

∂

′

∂

′

∂

′

∂

′

∂

′

∂

′

∂

′

∂

′′

∂

′

∂

ψψ

(34)

leading to spatiotemporal energy flux conservation

principles for each of the wave packets in the form

321

)0()0()0()0(

iiiiiiii

AwwwAwww =

(35)

Applying the CGO procedure in Sect. 1, we obtain

next generalized complex Riccati equations in the

form

3,2,1,,,1,

===+

′

jNiB

ijij



αε

(36)

where

′





















′

∂



lili

εε

(37)

Subsequently, from Eqs. (36,37) we obtain a set of

first order ordinary differential equations:

() ()

zwzw

ijijij

′

(38)

() ()

{}

()

111

ij ij

ij kj kl

wz w z w z

κκ

′′

=− +

′

















+−









′′′

















∏

(39)

We would like to emphasize that the above set of Eqs.

(38,39) takes a very simple form to be implemented

SpatiotemporalComplexGeometricalOptics(CGO)ofN3DInteractingAsymmetricGaussianWavePacketsinNonlinear

Medium-CGOastheSimplestandEfficientMethodforSpatiotemporalEvolution

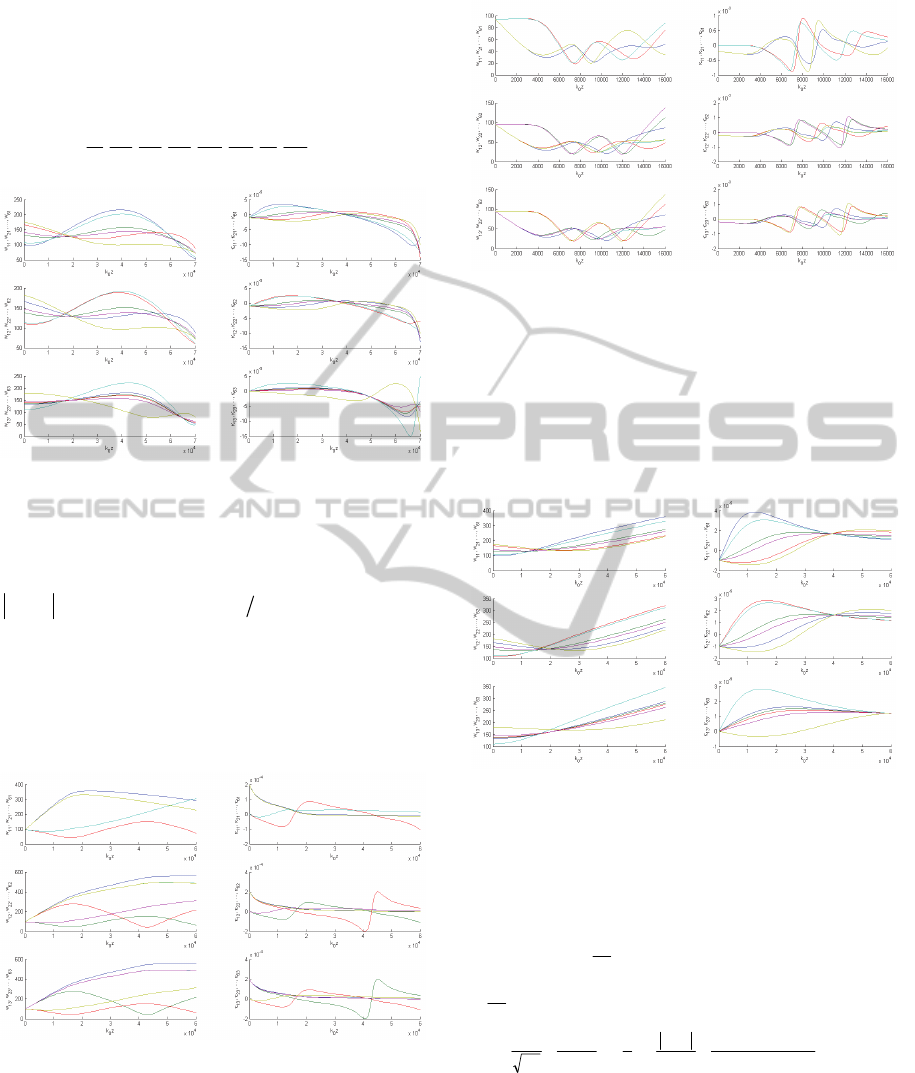
effectively in Matlab or Octave environments. It can

be observed that when we limit our consideration to

describe a single 3D wave packet propagating in a

nonlinear medium of Kerr type, we can also use a

variational procedure in the form

τηη

ττηηηη

dddzd

uuuuuu

uuL

,,,,,,,,,













∂



(40)

Figure 1: Evolution of 3D wave packets widths and chirps.

Parameters: linear permittivities 2

, diagonal

nonlinear permittivities

103

−

⋅=

, off-diagonal

nonlinear permittivities

109

−

⋅=

, initial amplitudes:

1)0( =

. Initial widths =

)0(

w [31, 53, 42; 42, 44,

43; 53, 35, 44; 34, 36, 35; 45, 47, 46; 56, 58, 57] are

presented in Matlab notation (i.e. semicolons separate rows,

colons separate elements in rows). Initial spatial chirps

-5

10)0()0( −==

κκ

and temporal one 0)0(

where

mn ≠

for

6,,2,1,, =lmn

Figure 2: Evolution of 3D wave packets widths and chirps.

Parameters: diagonal nonlinear permittivities

105.5

−

⋅=

, initial spatial and temporal widths

30)0( =

w , initial spatial and temporal chirps

=)0(

[2, 2, 2; 0, 0, 2; 0, 2, 0; 0, 2, 2; 2, 0, 2; 2, 2, 0]

−

⋅ , where

mn ≠

for

6,,2,1,, =lmn

. The

remaining parameters as in Figure 1.

Figure 3: Evolution of 3D wave packets widths and chirps.

Parameters: diagonal nonlinear permittivities

100.41339

−

⋅=

, off-diagonal nonlinear

permittivities

109

−

⋅=

, initial spatial and temporal

chirps

=)0(

[-2, -2, -2; 0, 0, -2; 0, -2, 0; 0, -2, -2; -2, 0,

-2; -2, -2, 0]

−

⋅ , where

mn ≠

for

6,,2,1,, =lmn

The remaining parameters as in Figure 1.

Figure 4: Evolution of 3D wave packets widths and chirps.

Parameters: diagonal and off-diagonal nonlinear

permittivities are equal

109

−

⋅==

nmnn

εε

for

6,,2,1, =mn

. The remaining parameters as in Figure 1.

to obtain a set of equations for the actual parameters

() ()

zwzw

jjj

′

111

(41)

() ()

{}

()

() () ()

































′

−













′

−=

′

131211

000

111

www

κκ

(42)

identical with the ones derived using CGO method.

However, we emphasize that authors of the paper

(Jirauschek, Morgner, Kartner, 2002) made a lot of

effort as compared with the simple and effective CGO

procedure presented above. Moreover, generalization

of variational procedure in Eq. (40) for N 3D wave

packets in the form

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology

τηη

ττηηηη

dddzd

uuuuuu

uuL

NNNNNNNN

,,,,,,,,,

,,,,,,,,,,







∂







∂





(43)

is very complicated. Numerical solutions of the set of

Eqs. (38,39) are shown in Figs. (1-4) where we

present the most interesting aspects of spatiotemporal

evolution of a 3D wave packet propagating in a

nonlinear medium. In these figures first of all we can

notice some effects which cannot be obtained for

single or pair of interacting wave packets. This way,

in Fig. 1 we notice a specific multi-wave collapse

effect. In Fig. 2, some of widths and chirps approach

stationary case. The remaining ones still collapse. In

Fig. 3 we notice oscillatory type of evolution, which

cannot be achieved for one or two interacting wave

packets. In the case of a number of interacting wave

packets, we notice the tendency for the packets to

imitate one another and approach one single state

shown in Fig. 4 in the form of crossing plots of chirps.

5 CONCLUSIONS

The CGO was applied for spatiotemporal evolution of

an arbitrary number of 3D mutually incoherent (with

different carrier frequencies) Gaussian wave packets

(GWPs) interacting and propagating in a nonlinear

medium of Kerr type. The wavelength is short as

compared to the overall size of the computational

domain and direct numerical schemes, such as split-

step fast Fourier method or finite differences beam

propagation method, to solve a wave equation

(Helmholtz and parabolic one) are very

computationally expensive. The proposed

approximation of geometrical optics with the

complex generalization on complex eikonal and

complex amplitude easily reduces the description of

the propagation of beam, pulse and wave packet to

solving complex ODEs. Numerical solving of ODE

(the dependence on

z) is much easier than solving

partial differential equations (PDE, the dependence

x, y, z) for the same problem. CGO leads to the

calculation of

N times M points arranged along the z-

axis. Other methods require the calculation of

N times

⋅ points, i.e. on a 3D mesh. With K

equalling 100, the calculations can be up to 10,000-

fold faster. This means that we obtain the results after

10 seconds in CGO instead of about 27 hours by other

means. In this way, CGO method enables to perform

very fast and efficient numerical simulations using

commonly available computer numerical software

like Matlab, Mathcad or Mathematica. CGO method

is especially useful for engineers demanding a

simpler method than those already used in nonlinear

optics (variational approach (VA) and the method of

moments (MM), which require the knowledge of

Hamilton optics formalism). The numerical

simulations performed in this paper show the

efficiency of the CGO method on the example of a

new sophisticated problem of nonlinear optics:

interaction of an arbitrary number of 3D Gaussian

wave packets propagating in a nonlinear (anomalous)

dispersive medium of Kerr type. We demonstrate that

the CGO method can describe also problems of

fundamental optics more illustratively than the

methods of Fourier transform and Fresnel diffraction

integral. Complementary to the presented results, an

on-line CGO solver is freely available at the authors’

website: http://slawek.ps.pl/odelia.html. We can state

that spatiotemporal CGO can be recognized to be the

simplest and the most practical approach among

commonly accepted methods of beam and fibre optics

such as: spectral analysis, variational method, method

of moments and method of generalized eikonal

approximation.

REFERENCES

S. A. Akhmanov, A. P. Sukhorukov, R. V. Khokhlov. Self-

focusing and light diffraction in nonlinear medium.

Soviet Phys. Uspekhi 10, 609-636 (1968).

D. Anderson. Variational approach to nonlinear pulse

propagation in optical fibers. Physical Review A, vol.

27, No. 6, pp. 3135-3145, (1983).

J. A. Arnaud,. Beams and Fiber Optics, Academic Press,

New York, (1976).

P. Berczynski and Yu. A. Kravtsov. Theory for Gaussian

beam diffraction in 2D inhomogeneous medium, based

on the eikonal form of complex geometrical optics,

Phys. Lett. A, 331, 265−268 (2004).

P. Berczynski. Complex geometrical optics of nonlinear

inhomogeneous fibres. Journal of Optics 13 035707

(2011).

P. Berczynski. Complex geometrical optics of

inhomogeneous and nonlinear saturable media, Optics

Communications 295, 208–218, (2013).

P. Berczynski and S. Marczynski. Chapter One: Gaussian

Beam Propagation in Inhomogeneous Nonlinear

Media: Description in Ordinary Differential Equations

by Complex Geometrical Optics. Advances in Imaging

and Electron Physics, (Edited by Peter W. Hawkes),

Vol. 185, ISBN: 978-0-12-800144-8, Pages 1–111,

(2014).

SpatiotemporalComplexGeometricalOptics(CGO)ofN3DInteractingAsymmetricGaussianWavePacketsinNonlinear

Medium-CGOastheSimplestandEfficientMethodforSpatiotemporalEvolution

M. Born, E. Wolf. Principles of Optics, New York:

Pergamon, (1959).

S. Choudhary, L. B. Felsen. Analysis of Gaussian beam

propagation and diffraction by inhomogeneous wave

tracking. Proceedings of the IEEE, vol. 62, No.11,

(1974).

G. A. Deschamps. Gaussian beam as a bundle of complex

rays. Electron. Lett., 7(23), 684-685, (1971).

G. A. Deschamps and P. E Mast,. Beam tracing

and applications. In: Proc. Symp. Quasi-Optics, pp.

379-395, Polytechnic Press, New York, (1964).

L. Felsen. Evanescent waves. J. Opt. Soc. Am., vol. 66, No.

8, p. 751-754, (1976).

Ch. Jirauschek, U. Morgner, F. X. Kartner, Variational

analysis of spatiotemporal pulse dynamics in dispersive

Kerr media, pp 1716-17-21, J.Opt.Soc.Am. B 19, Vol.

19, No. 7, (2002).

M. Kline and I. Kay. Electromagnetic theory and

Geometrical Optics. Pure and Applied Mathematics, A

Series of Texts and Monographs Edited by R. Courant,

L. Bers and J. Stoker, vol.12, John Wiley and Sons, Inc.

(1965).

H. Kogelnik, On the Propagation of Gaussian Beams of

Light Through Lenslike Media Including those with a

Loss or Gain Variation. Applied Optics, 4(12), 1562 -

1569, (1965).

Yu A. Kravtsov N. Y. Zhu. Theory of diffraction: Heuristic

Approaches, Alpha Science International, ISBN

1842653725, (2009).

Yu. A. Kravtsov, Complex rays and complex caustics,

Radiophys. Quantum Electronics 10, 719−730,

(1967).

R. K. Luneburg,. Mathematical Theory of Optics.

University of California Press, Berkeley and Los

Angeles, (1964).

E. G. Sauter. Nonlinear Optics. John Wiley&Son, p. 1-214,

NY 10158-0012, published in Canada, (1996).

A. Sommerfeld. Optics, Lectures on theoretical physics,

vol. 4, New York: Academic Press, (1964).

S. N. Vlasov, V. A. Petrischev and V. I. Talanov. Averaged

description of wave beams in linear and nonlinear

media (The method of moments), Radiofizika, vol. 14,

No. 9, pp. 1353-1363, (1971).

S. Yap, B. Quek and K. Low. Generalized eikonal

approximation. 1. Propagation of electromagnetic pulse

in a linear dispersive medium, 2. Propagation of

stationary electromagnetic waves in linear and

nonlinear media, JOSA A, vol. 15, 2725-2729; vol.15,

2720-2724, (1998).

PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology