Quantifying Depth and Complexity of Thinking and Knowledge

Tamal T. Biswas and Kenneth W. Regan

Department of CSE, University at Buffalo, Amherst, 14260, NY, U.S.A.

Keywords:

Decision Making, Depth of Search, Chess, Item Difﬁculty, Judging of Learning Agents, Knowledge Repre-

sentation.

Abstract:

Qualitative approaches to cognitive rigor and depth and complexity are broadly represented by Webb’s Depth

of Knowledge and Bloom’s Taxonomy. Quantitative approaches have been relatively scant, and some have

been based on ancillary measures such as the thinking time expended to answer test items. In competitive

chess and other games amenable to incremental search and expert evaluation of options, we show how depth

and complexity can be quantiﬁed naturally. We synthesize our depth and complexity metrics for chess into

measures of difﬁculty and discrimination, and analyze thousands of games played by humans and computers

by these metrics. We show the extent to which human players of various skill levels evince shallow versus

deep thinking, and how they cope with ‘difﬁcult’ versus ‘easy’ move decisions. The goal is to transfer these

measures and results to application areas such as multiple-choice testing that enjoy a close correspondence in

form and item values to the problem of ﬁnding good moves in chess positions.

1 INTRODUCTION

Difﬁculty, complexity, depth, and discrimination are

important and related concepts in cognitive areas such

as test design, but have been elusive to quantify.

Qualitative approaches are legion: Bloom’s taxon-

omy (Bloom, 1956; Krathwohl et al., 1973; Ander-

son and Krathwol, 2001), Webb’s Depth of Knowl-

edge Guide (Webb, 1997), Bransford et al.’s studies of

learning (Bransford et al., 2000; Donovan and Brans-

ford, 2005). Quantitative approaches have mainly ei-

ther inferred values from performance data, such as

results on large-scale tests (Morris et al., 2006; Hotiu,

2006), or have measured ancillary quantities, such as

deliberation time in decision ﬁeld theory (Busemeyer

and Townsend, 1993) or estimations of risk (Tversky

and Kahneman, 1992).

Our position is to approach these concepts by

starting in a domain where they can be clearly for-

mulated, cleanly quantiﬁed, and analyzed with large

data. Then we aim to transfer the formulations,

results, and conclusions to domains of wider in-

terest. Our home domain is competitive chess, in

which the items are thousands to millions of positions

from recorded games between human players in var-

ious kinds of high-level tournaments. Work to date

(Chabris and Hearst, 2003; Haworth, 2003; Guid and

Bratko, 2006, 2011; Regan and Haworth, 2011) has

established solid relationships between quality mea-

sures arising from direct analysis of players’ move de-

cisions and standard skill assessment metrics in chess,

mainly grades of mastery and the Elo rating system.

Some prior work (Chabris and Hearst, 2003; Moxley

et al., 2012) has extended the correspondence to time

available and/or taken for (move) decisions, but this

is still short of isolating depth or difﬁculty as factors.

Our aims are helped by similarities between the

tasks of ﬁnding an optimal move (or at least a good

move) in a chess position and ﬁnding the best answer

to a multiple-choice question (or at least a good an-

swer in case there are partial credits). There are also

mathematical correspondences between the Elo rating

system (Elo, 1978; Glickman, 1999) and metrics in

Rasch modeling (Rasch, 1961; Andersen, 1973; An-

drich, 1978; Masters, 1982; Andrich, 1988; Linacre,

2006; Ostini and Nering, 2006), item-response theory

(Baker, 2001; Morris et al., 2006; Thorpe and Favia,

2012), and other parts of psychometrics.

Elo ratings r

of players P maintain a logistic-

curve relationship between the expected score of P

over an opponent Q and the rating difference r

− r

A difference of 200 points gives roughly 75% expec-

tation, and this has produced a scale on which 2200

is recognized as “master,” the highest few players

are over 2800, and many computer chess engines are

rated well over 3000 even on inexpensive hardware.

The engines can hence act as an objective and author-

itative “answer key” for chess positions.

602

Biswas T. and Regan K..

Quantifying Depth and Complexity of Thinking and Knowledge.

DOI: 10.5220/0005288306020607

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 602-607

ISBN: 978-989-758-074-1

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

Essentially all engines give values in standard

units of centipawns and use iteratively deepened

search. That is, beginning with d = 1 (or some other

ﬂoor value) they search to a basic depth of d plies

(meaning moves by White or Black, also called half-

moves), give values v

i,d

to each legal move m

at that

depth d, and then deepen the search to depth d + 1.

This incremental search can be capped at some ﬁxed

maximum depth D. Based on depth-to-strength esti-

mates by Ferreira Ferreira (2013) for the Houdini 1.5a

engine and matches run by us between it and versions

2.3.1 and 3 of the Stockﬁsh engine used for the re-

sults reported here, we estimate depth 19 of the latter

(in so-called Multi-PV analysis mode) at 2650 ±50.

Taking care to begin with an empty hash table for

each position in each game, we use Stockﬁsh’s val-

ues v

i,d

for 1 ≤ d ≤ D = 19 to quantify our key con-

cepts. Our measures are weighted so that values of

poor moves have little effect, so we could effectively

bound the number of legal moves at ` = 50. We con-

sider moves ordered so that v

1,D

≥ v

2,D

≥ ··· ≥ v

`,D

at the highest depth, but of course the highest value

∗

for d < D might equal v

i,d

where i > 1. We actu-

ally work in terms of the differences v

∗

− v

i,d

, and in

order to reﬂect that differences matter less when one

side has a large advantage, we further scale them by

deﬁning

i,d

x=v

∗

x=v

i,d

1 + a|x|

dx.

Here the constant a might be engine-dependent but

we ﬁx a = 1 since we used only two closely-related

Stockﬁsh versions. Cases where v

∗

is positive but v

i,d

is negative (meaning that move m

is an error leading

from advantage to disadvantage) are handled by doing

the integral in two pieces. All δ

i,d

values are nonneg-

ative, and are 0 for the optimal move at each depth

and any other moves of equal value. The key idea of

swing is exempliﬁed by these two cases:

• A move m

swings up if v

i,d

< v

j,d

for some other

moves m

at low depths d, but v

i,d

≥ v

j,d

for (al-

most) all other m

for depths d at or near the max-

imum analyzed depth D.

• The move swings down—and intuitively is a

“trap” to avoid—if it has one of the highest values

at low depths, but is markedly inferior to the best

move m

at the highest depth: v

i,D

 v

1,D

= v

∗

It is expected in the former case that v

i,D

> v

i,d

for

lower depths d, and in the latter that v

i,D

 v

i,d

, so

that a swinging move changes its absolute value, but

it is its value relative to other moves that is primarily

assessed.

2 METRICS AND RATINGS

At each depth d, the chess program produces an or-

dered list L

of moves and their values. Comparing

these lists L

for different d involves standard prob-

lems in preference and voting theory, with the twist

that high values from poor moves have diminished

weight. We speak of rating aggregation rather than

rank aggregation because the values of each move,

not just the ordinal ranks, are important.

We postulate that swing should be a signed quan-

tity in centipawn units that pertains to an individual

move option, while complexity should be nonnegative

and dimensionless and pertain to a position overall.

Swing should reﬂect a bulk comparison of L

for low

d versus high d, while complexity can be based on

how L

changes to L

d+1

in each round of search. Thus

for complexity we may employ some divergence mea-

sure between ordered sequences X = (x

), Y = (y

)

and sum it up over all d. Whereas common voting

and preference applications give equal weight to all

choices, we wish to minimize the effects of apprecia-

bly sub-optimal moves.

Any anti-symmetric difference function µ(x

)

gives rise to the generalized Kendall tau coefﬁcient

X,Y

∑

i, j

µ(x

)µ(y

)

||µ

|| · ||µ

, (1)

where ||µ

|| =

∑

i, j

µ(x

)

and ||µ

|| is deﬁned

similarly. Then always −1 ≤ τ

X,Y

≤ +1, with +1

achieved when Y = X and −1 when Y = −X. If

µ is homogeneous, so that µ(cx

,cx

) = c

µ(x

)

where c

depends only on c, then τ

X,Y

becomes scale-

invariant in either argument: τ

X,cY

= τ

cX,Y

= τ

X,Y

The usual difference function µ(x

) = x

− x

linear, and also invariant under adding a ﬁxed quantity

to each value. It is not, however, invariant under aug-

menting the lists with irrelevant alternatives having

low ratings. We swap these properties by employing

µ(x

) =

− x

+ x

instead. When either x

or x

is large, say of order

K representing a poor move, then µ(x

) will have

order at most 1/K. Assuming that the same move is

poor in Y , the augmentation will add terms of order

only 1/K

to the numerator and denominator of (1),

yielding little change. This naturally conﬁnes atten-

tion to reasonable moves at any juncture. We deﬁne

the complexity κ(π) of a position π, for d ranging from

the minimum available depth d

to D − 1, by:

κ(π) = 1 −

D − 1

D−1

∑

d=1

d+1

QuantifyingDepthandComplexityofThinkingandKnowledge

603

Notice that high agreement (τ always near 1) ﬂips

around to give complexity κ near 0. The deﬁnition

of complexity might be modiﬁed by weighting higher

depths differently from lower depths.

To deﬁne the swing of a move m

we use a simple

sum of scaled differences in value between depth d

and the highest depth D, rather than average or other-

wise weight them over d:

sw(m

) =

∑

d=1

(δ

i,d

− δ

i,D

This is a signed quantity—if positive it means that the

value of move m

“swings up”, while negative means

it “swings down”—in the manner of falling into a

trap. The overall “swinginess” of a position π, how-

ever, is a non-negative quantity. It is convenient ﬁrst

to deﬁne it between any two depths d and e:

d,e

(π) =

∑

i=1

|δ

i,d

− δ

i,e

For overall swing it is expedient to dampen the ef-

fect of moves for which δ

i,d

is large. Unlike the case

with Kendall tau, we want to dampen a difference

|δ

i,d

−δ

i,e

| only if both values are large. We also wish

to divide by a dimensionless quantity, in order to pre-

serve the centipawn units of swing. Hence we postu-

late a scaling factor c that might depend on the chess

program, and divide by an exponential function of the

harmonic mean of the deltas divided by c:

ν(δ,δ

) = exp



−2δδ

c(δ + δ

)



Since this paper uses only one chess program, we

again take c = 1. Thus we deﬁne the damped over-

all swing between depths d and e by:

∗

d,e

(π) =

∑

i=1

ν(δ

i,d

,δ

i,e

)|δ

i,d

− δ

i,e

Then the swing at depth d is given by s

∗

d,d+1

(π), while

the aggregate swing to the highest depth is deﬁned by

S(π) =

D−1

∑

d=1

∗

d,D

We employ weighted versions of this to deﬁne our key

concepts. We desire the measure of difﬁculty to be in

units of depth rather than centipawns. Our idea is that

a position is deeper, hence more difﬁcult, if most of

the swing occurs at higher depths. It is OK to multiply

it by the complexity since that is dimensionless.

Accordingly, we ﬁrst deﬁne the relative depth ρ

to be the depth below which half of the swing has

occurred. For this we add up the swing from each

depth to the next, rather than the swing relative to the

highest depth. With respect to nonnegative weights

w(d) summing to 1, deﬁne

Σ(π) =

D−1

∑

d=1

w(d)s

∗

d,d+1

(π).

We used w(d) = d normalized by

∑

D−1

d=1

d. Then, let-

ting Σ

(π) be the sum up to e rather than D−1, deﬁne

ρ(π) = max{e : Σ

(π) ≥

Σ(π)} − ψ,

where the adjustment ψ term for the indicated e is

ψ =

(π) −

Σ(π)

w(e − 1)s

∗

e−1,e

(π)

Finally, we stipulate that the analyzed difﬁculty of a

position π is given by

Diff (π) = κ(π) · ρ(π).

For calculating the discrimination we use the rel-

ative depth of the position. We evaluate the mean

and standard deviation σ

of s

∗

d,D

values where

d ∈ (1, e − 1) (e = ρ(π)) and mean α

and standard

deviation σ

of s

∗

d,D

values where d ∈ (e,D − 1).

The discrimination parameter Ψ of the position π

can then be evaluated as:

Ψ(π) = (α

− α

)(

)

∑

i, j

∗

i,D

− s

∗

j,D

)

∑

i, j

The weights w

i, j

= 1/( j − i) where i ∈ [l] and j ∈ [r]

ensures more emphasize to the depths near the difﬁ-

culty of the position while calculating discrimination.

Our ﬁrst of two main datasets comprised all

recorded games in standard round-robin

tournaments

in 2006–2009 between players each within 10 Elo

of a “milepost” value. The mileposts used were Elo

2200, 2300, 2400, 2500, 2600, and 2700. The sec-

ond comprised all 900 games of the 2013 World Blitz

(WB) Championship, which was held in Khanty-

Mansiysk, Russia, and distinguished by giving an ac-

curate record of the moves of every game. This form

of blitz, 3 minutes per game plus an increment of 2

seconds per move, is comparable to the historical “5-

minute” form of blitz, and gives markedly less time

than the minimum 90 minutes plus 30 seconds per

move of the “milepost” games. Our idea was to test

whether the blitz games were played at an identiﬁably

lower level of depth. The average rating of the 60 WB

players was 2611.

“Small Swiss” events with up to 64 players over 9

rounds were also included.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

604

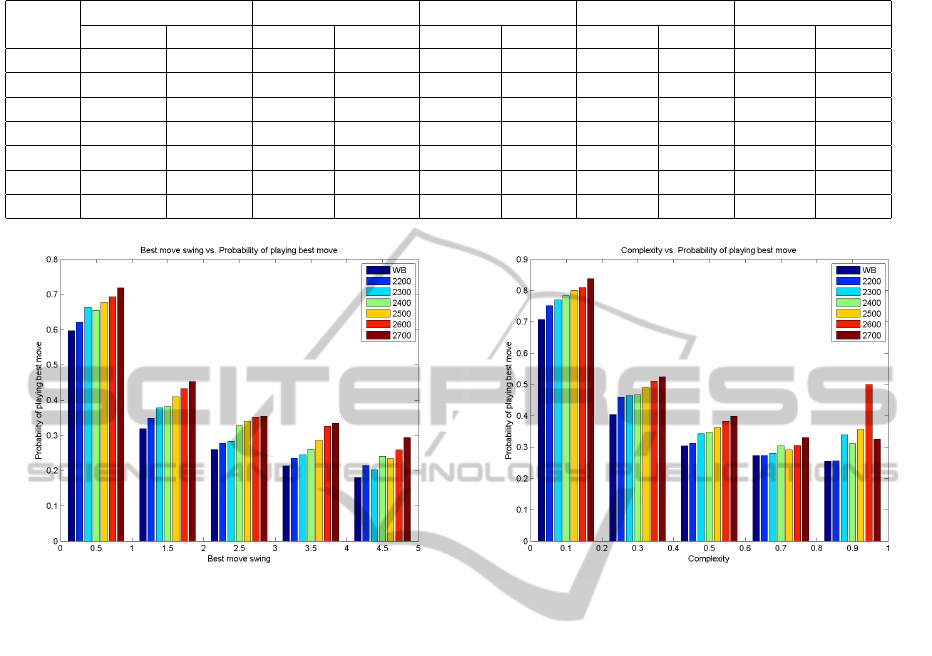
Table 1: Best move and number of total moves played various swing.

Swing < 1 1 ≤ Swing < 2 2 ≤ Swing < 3 3 ≤ Swing < 4 4 ≤ Swing ≤ 5

Level #EMP TM #EMP TM #EMP TM #EMP TM #EMP TM

WB 22,785 38,150 3,523 11,025 1,542 5,920 697 3,267 825 4,566

2200 4,954 7,967 812 2,331 364 1,308 184 781 220 1,025

2300 8,081 12,164 1,413 3,740 575 2,030 303 1,235 350 1,731

2400 8,878 13,536 1,575 4,127 754 2,296 340 1,301 493 2,049

2500 7,203 10,620 1,374 3,351 691 2,040 332 1,162 383 1,635

2600 3,252 4,689 701 1,619 323 918 165 507 213 823

2700 2,823 3,927 596 1,315 261 737 144 430 208 708

Figure 1: Frequency of playing engine moves with different

swing values.

3 RESULTS

Our results show that the raw factor of swing makes

a large impact on the ability of players at all levels

to ﬁnd the optimal move m

identiﬁed (at the high-

est depth) by the engine, and that this carries forward

to our more-reﬁned difﬁculty and discrimination mea-

sures. The WB games seemed to function as if they

were a rating level below 2200, most often in the

range 1800 to 2100.

Table 1 gives the total moves (TM) and times with

the engine’s move played (EMP) for each of ﬁve inter-

vals of swing values sw(m

), and Figure 1 graphs the

frequencies of m

being played in each case. The plot

clearly indicates that high-swing moves are “tricky”

for players to ﬁnd—the players more often chose infe-

rior moves. The phenomenon is consistent with play-

ers of any Elo ratings, where higher rated players are

slightly less tricked by the swing values. This feature

is more prominent in the blitz tournament. Quick de-

cision making often leads to pick inferior moves, or

where the virtue of the engine move was not obvious

at lower depths.

In our implementation, we rank the possible

Figure 2: Frequency of playing engine moves for position

with various complexity.

moves at any particular position based on the order

provided by the chess engines. Often the ﬁrst move

listed by the engine shows less swing, and make it

attractive choice for the players from the beginning.

Earlier studies show that players often chose the ﬁrst

move listed by the engine 58% of the time whereas the

second move is chosen only 42% of the time. Table 2

shows that in fact the ﬁrst listed move often has much

lower swing with comparison to the other tied moves.

This is true for players across any ability level.

Figure 2 represents the probability of playing the

best move for positions of various complexity. The

probability gets monotonically decreased. The ran-

dom noise seen at positions with higher complexity is

due to insufﬁcient number of samples(see Table 3).

Figure 3 demonstrates difﬁculty and best-move

probability for various positions. The ﬁgure clearly

shows that players of all calibers could ﬁnd the best

move when the position is easy, but less than 50%

of the time when the difﬁculty lies between 4 and 5.

Table 4 shows the distribution of data across various

difﬁculty levels. Figure 4 shows a similar but lesser

effect for our measure of discrimination.

QuantifyingDepthandComplexityofThinkingandKnowledge

605

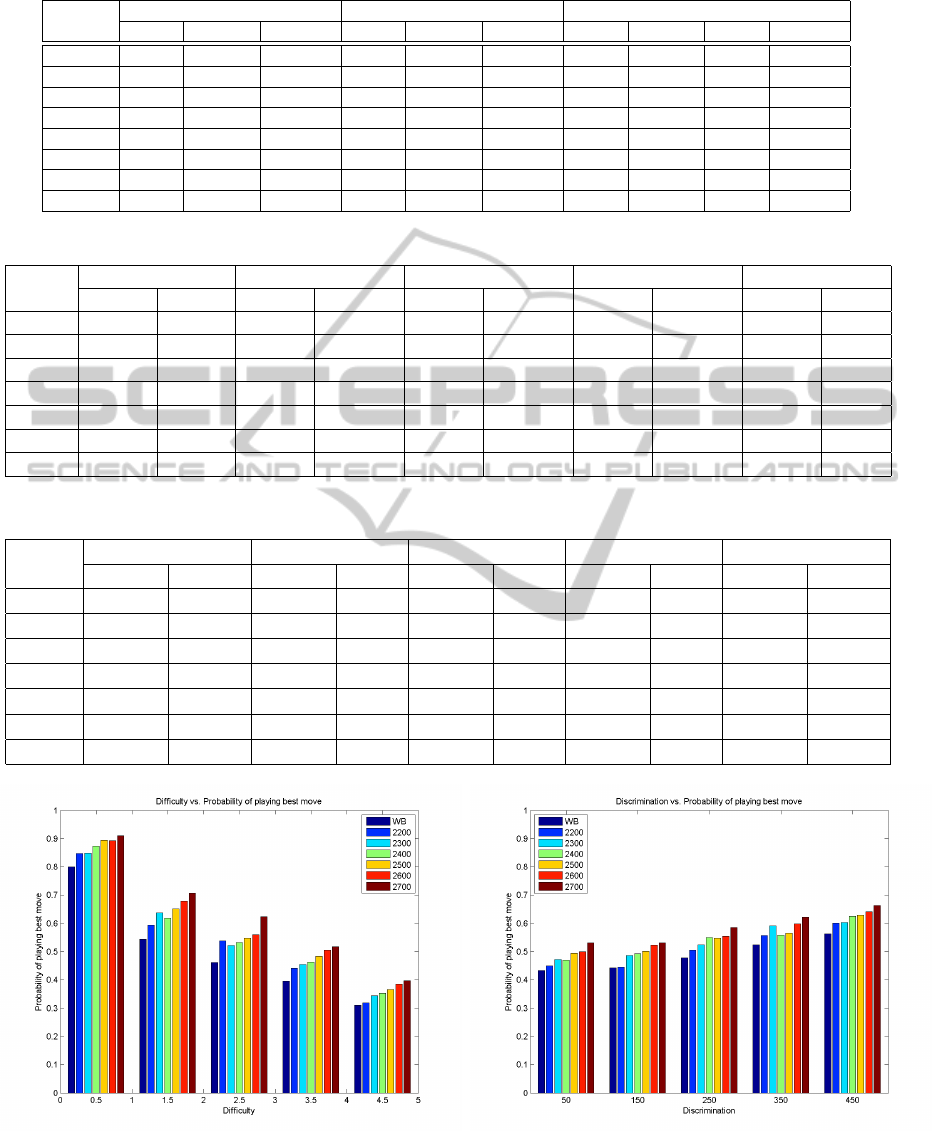
Table 2: Swing for Tied moves.

Any # of Tied Moves 2 Tied Moves 3 Tied Moves

Level First Second #Moves First Second #Moves First Second Third #Moves

WB 1.168 1.903 12,163 1.383 2.073 6,580 1.246 2.051 2.646 1,661

2200 1.263 1.912 2,447 1.430 2.056 1,391 1.141 2.005 2.265 329

2300 1.310 2.063 3,731 1.530 2.233 2,120 1.333 2.061 2.782 516

2400 1.330 1.964 4,270 1.555 2.178 2,514 1.211 1.841 2.449 569

2500 1.380 2.154 3,309 1.538 2.302 1,981 1.318 2.127 2.782 476

2600 1.408 2.216 1,607 1.533 2.349 974 1.244 2.338 3.083 242

2700 1.558 2.106 1,255 1.737 2.292 755 1.411 2.011 2.614 210

Overall 1.273 1.989 28,782 1.477 2.163 16,315 1.260 2.043 2.645 4,003

Table 3: Number of times best move played vs. number of total moves at positions of various complexity

0 ≤ Cpx. < 0.2 0.2 ≤ Cpx. < 0.4 0.4 ≤ Cpx. < 0.6 0.6 ≤ Cpx. < 0.8 0.8 ≤Cpx. ≤ 1

Level #EMP TM #EMP TM #EMP TM #EMP TM #EMP TM

WB 14851 20983 7804 19270 5216 17155 1395 5104 106 416

2200 3083 4098 1863 4051 1216 3894 340 1244 32 125

2300 5227 6779 2933 6308 1984 5790 519 1849 59 174

2400 5672 7236 3421 7315 2282 6574 619 2036 46 148

2500 4590 5731 2916 5923 1946 5369 474 1625 57 160

2600 2061 2547 1384 2706 954 2496 232 761 23 46

2700 1840 2197 1146 2182 830 2084 200 605 16 49

Table 4: Best move and number of total moves for positions with various difﬁculty.

Diff. < 1 1 ≤ Diff. < 2 2 ≤ Diff. < 3 3 ≤ Diff. < 4 4 ≤ Diff. ≤ 5

Level #EMP TM #EMP TM #EMP TM #EMP TM #EMP TM

WB 10438 13038 3790 6979 3462 7497 3189 8049 8493 27365

2200 2178 2569 754 1269 853 1585 741 1680 2008 6309

2300 3666 4318 1333 2089 1278 2450 1211 2665 3234 9378

2400 3925 4492 1481 2396 1463 2743 1452 3133 3719 10545

2500 3140 3512 1205 1848 1262 2304 1189 2459 3187 8685

2600 1392 1558 572 843 558 996 605 1198 1527 3961

2700 1183 1300 538 761 534 855 460 888 1317 3313

Figure 3: Frequency of playing engine moves for position

with various difﬁculty.

Figure 4: Frequency of playing engine moves for position

with various discrimination.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

606

4 CONCLUSION AND PROSPECTS

We have deﬁned quantitative measures for qualitative

concepts of depth, difﬁculty, complexity, and discrim-

ination. The deﬁnitions are within a speciﬁc model of

decision making at chess, but use no feature of chess

apart from utility values of decision options, and are

framed via mathematical tools that work across ap-

plication areas. For the ﬁrst three, we have shown

a strong response effect on performance, though we

have not distinguished the measures from each other.

The effect shows across skill levels and persists when

restricting to controlled cases such as moves of equal

highest-depth value.

REFERENCES

Andersen, E. (1973). Conditional inference for multiple-

choice questionnaires. Brit. J. Math. Stat. Psych.,

26:31–44.

Anderson, L. and Krathwol, D. (2001). A Taxonomy for

Learning, Teaching, and Assessing: A revision of

Blooms taxonomy of educational objectives: complete

edition. Longman, New York.

Andrich, D. (1978). A rating scale formulation for ordered

response categories. Psychometrika, 43:561–573.

Andrich, D. (1988). Rasch Models for Measurement. Sage

Publications, Beverly Hills, California.

Baker, F. B. (2001). The Basics of Item Response Theory.

ERIC Clearinghouse on Assessment and Evaluation.

Bloom, B. (1956). Taxonomy of Educational Objectives,

Handbook I: The Cognitive Domain. David McKay

Co., New York.

Bransford, J. D., Brown, A., and Cocking, R., editors

(2000). How People Learn: expanded edition. The

National Academies Press, Washington, D.C.

Busemeyer, J. R. and Townsend, J. T. (1993). Decision

ﬁeld theory: a dynamic-cognitive approach to deci-

sion making in an uncertain environment. Psycholog-

ical review, 100(3):432.

Chabris, C. and Hearst, E. (2003). Visualization, pattern

recognition, and forward search: Effects of playing

speed and sight of the position on grandmaster chess

errors. Cognitive Science, 27:637–648.

Donovan, M. S. and Bransford, J. D. (2005). How Students

Learn. The National Academies Press, Washington,

D.C.

Elo, A. (1978). The Rating of Chessplayers, Past and

Present. Arco Pub., New York.

Ferreira, D. (2013). The impact of search depth on chess

playing strength. ICGA Journal, 36(2):67–80.

Glickman, M. E. (1999). Parameter estimation in large dy-

namic paired comparison experiments. Applied Statis-

tics, 48:377–394.

Guid, M. and Bratko, I. (2006). Computer analysis of world

chess champions. ICGA Journal, 29(2):65–73.

Guid, M. and Bratko, I. (2011). Using heuristic-search

based engines for estimating human skill at chess.

ICGA Journal, 34(2):71–81.

Haworth, G. (2003). Reference fallible endgame play.

ICGA Journal, 26:81–91.

Hotiu, A. (2006). The relationship between item difﬁculty

and discrimination indices in multiple-choice tests in

a physical science course. M.Sc. thesis.

Krathwohl, D., Bloom, B., and Bertram, B. (1973). Taxon-

omy of Educational Objectives, the Classiﬁcation of

Educational Goals. Handbook II: Affective Domain.

David McKay Co., New York.

Linacre, J. M. (2006). Rasch analysis of rank-ordered data.

Journal of Applied Measurement, 7(1).

Masters, G. (1982). A Rasch model for partial credit scor-

ing. Psychometrika, 47:149–174.

Morris, G. A., Branum-Martin, L., Harshman, N., Baker,

S. D., Mazur, E., Dutta, S., Mzoughi, T., and Mc-

Cauley, V. (2006). Testing the test: Item response

curves and test quality. American Journal of Physics,

74(5):449–453.

Moxley, J. H., Ericsson, K. A., Charness, N., and Krampe,

R. T. (2012). The role of intuition and deliberative

thinking in experts’ superior tactical decision-making.

Cognition, 124(1):72 – 78.

Ostini, R. and Nering, M. (2006). Polytomous Item Re-

sponse Theory Models. Sage Publications, Thousand

Oaks, California.

Rasch, G. (1961). On general laws and the meaning of

measurement in psychology. In Proceedings, Fourth

Berkeley Symposium on Mathematical Statistics and

Probability, pages 321–334. University of California

Press.

Regan, K. and Haworth, G. (2011). Intrinsic chess ratings.

In Proceedings of AAAI 2011, San Francisco.

Thorpe, G. L. and Favia, A. (2012). Data analysis using

item response theory methodology: An introduction

to selected programs and applications. Psychology

Faculty Scholarship, page 20.

Tversky, A. and Kahneman, D. (1992). Advances in

prospect theory: Cumulative representation of uncer-

tainty. Journal of Risk and Uncertainty, 5:297–323.

Webb, N. (1997). Criteria for Alignment of Expectations

and Assessments on Mathematics and Science Educa-

tion. Monograph No. 6. CCSSO, Washington, DC.

QuantifyingDepthandComplexityofThinkingandKnowledge

607