Alpha Complexes in Protein Structure Prediction

Pawel Winter and Rasmus Fonseca

Department of Computer Science, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen Ø, Denmark

Keywords:

Protein Structure Prediction, Force Field, Alpha-complexes, Kinetic Data Structures.

Abstract:

Reducing the computational effort and increasing the accuracy of potential energy functions is of utmost

importance in modeling biological systems, for instance in protein structure prediction, docking or design.

Evaluating interactions between nonbonded atoms is the bottleneck of such computations. It is shown that

local properties of α-complexes (subcomplexes of Delaunay tessellations) make it possible to identify non-

bonded pairs of atoms whose contributions to the potential energy are not marginal and cannot be disregarded.

Computational experiments indicate that using the local properties of α-complexes, the relative error (when

compared to the potential energy contributions of all nonbonded pairs of atom) is well within 2%. Further-

more, the computational effort (assuming that α-complexes are given) is comparable to even the simplest and

therefore also fastest cutoff approaches.

The determination of α-complexes from scratch for every conﬁguration encountered during the search for the

native structure would make this approach hopelessly slow. However, it is argued that kinetic α-complexes can

be used to reduce the computational effort of determining the potential energy when “moving” from one con-

ﬁguration to a neighboring one. As a consequence, relatively expensive (initial) construction of an α-complex

is expected to be compensated by subsequent fast kinetic updates during the search process.

Computational results presented in this paper are limited. However, they suggest that the applicability of α-

complexes and kinetic α-complexes in protein related problems (e.g., protein structure prediction and protein-

ligand docking) deserves furhter investigation.

1 INTRODUCTION

In protein structure prediction a vast atomic conﬁgu-

ration space has to be searched when looking for the

native conﬁguration minimizing its potential energy.

Good potential energy estimators require substantial

computational effort. Reducing this effort is therefore

important. Furthermore, similar searches and poten-

tial energy estimations arise in for example protein-

protein docking and in protein design.

Interactions between nonbonded atoms are the

computational bottleneck of potential energy estima-

tions. Commonly used cutoff methods compute the

distances between all pairs of nonbonded atoms and

calculate the contributions of those within some pre-

speciﬁed cutoff distance. Different types of contribu-

tions such as van der Waals and Coulomb potentials

may require different cutoff values (Schlick, 2010).

Hierarchical decompositions of proteins with appro-

priately chosen bounding volumes have also been

used to speed up potential energy estimations (Lotan

et al., 2004; Winter and Fonseca, 2012). We show

that α-complexes (which are subcomplexes of well-

known Delaunay tessellations) for appropriately cho-

sen real values of α, α ≥ 0, are well-suited for the

identiﬁcation of nonbonded pairs of atoms essential

for the estimation of potential energy of proteins. The

identiﬁcation of such pairs involves exploiting the

structural properties of α-complexes while making

the distance computations for cutoff purposes unnec-

essary. Computational experiments reported in this

paper indicate that the relative error is well within

2% while the computational effort is comparable with

even the simplest cutoff approaches.

Searching for a conﬁguration minimizing the po-

tential energy typically involves perturbing one con-

ﬁguration to obtain the next. It can for example

be achieved by small dihedral rotations of covalent

bonds. As these rotations are carried out, the under-

lying α-complexes can be appropriately updated. We

sketch how these updates can be carried out using the

kinetic data structure framework. In particular, bond

rotations imply that groups of atoms rotate around the

same axis with the same rotational speed on circular

orbits in parallel planes. This signiﬁcantly speeds up

the computations needed to update α-complexes. Fast

178

Winter P. and Fonseca R..

Alpha Complexes in Protein Structure Prediction.

DOI: 10.5220/0005251401780182

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2015), pages 178-182

ISBN: 978-989-758-070-3

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

updates, in turn, imply fast determination of potential

energy for the next neighboring conﬁguration.

2 SYSTEMS AND METHODS

A force ﬁeld is a collection of parameters and math-

ematical expressions that together deﬁne a function

approximating the potential energy of a system of

atoms. Such a function typically includes bonded

terms capturing forces between covalently bonded

atoms and nonbonded terms capturing forces of non-

bonded atoms.

A simple but still reasonable force ﬁeld approx-

imating the potential energy (in kcal/mol) of a par-

ticular conformation of a protein (Levitt et al., 1995;

Schlick, 2010) is given by E = E

+ E

where the E

term comprises the contributions from bonded atoms

and the E

term comprises the potential energy con-

tributions from nonbonded atoms. It is deﬁned by

= E

+ E

, where

∑

p=(i, j)

i j

[

i j

]

−2e

i j

[

i j

]

)

and

= 332

∑

p=(i, j)

i j

where p is a pair of atoms i and j, r

i j

= (r

+ r

)/2

with r

and r

being van der Waals radii of interacting

atoms, r

i j

is the actual distance between the atoms i

and j, e

i j

√

with e

and e

being partial charge

parameters of interacting atoms. Finally, q

and q

are

partial charges of the atoms i and j.

Nonbonded interactions between atoms separated

by less than three bonds along the covalent structure

are disregarded (Levitt et al., 1995). Their interac-

tions are assumed to be accounted for by bonded in-

teractions.

It is evident that nonbonded terms depend on the

distances between interacting atoms. As the distances

grow, the potential energy contributions become neg-

ligible. In order to speed up the computations, van der

Waals interactions between atoms more than 8-12

apart can be disregarded. The cutoff distance for E

is higher (Levitt et al., 1995). Other, more sophisti-

cated cutoff techniques have been suggested (Schlick,

2010).

3 ALGORITHMS

An α-ball b

centered at a point p with radius α,

α ≥0, is the set of points at most α away from p. Let

S be a set of n points in the 3-dimensional Euclidean

space E

. Let T be a subset of S of size |T | = k + 1,

0 ≤ k ≤3. The convex hull σ

of T is also referred to

as a k-simplex. Given a k-simplex σ

, any k

-simplex

, T

⊂T , is a (proper) face of σ

. A k-simplex σ

0 ≤ k ≤ 3, belongs to the Delaunay complex, (DC )

iff there exists a sphere that passes through the points

of T and all other points of S are strictly outside this

sphere. Assuming the general position (i.e., no ﬁve

points lie on a common sphere), the Delaunay com-

plex is a simplicial complex.

Let b

denote the smallest ball that passes through

the points of a k-simplex T , 0 ≤ k ≤ 3. Let ρ

de-

note the radius of b

. If b

contains no point of S

in its interior, σ

is called Gabriel. Let α be a pos-

itive real number. T is said to be α-short if ρ

≤ α.

The α-complex S

consists of Delaunay simplices that

are Gabriel and α-short together with their proper

faces (Edelsbrunner, 1992).

Since S

⊆S

for α

≤α

, α-complexes provide

a ﬁltration of a growing family of simplicial com-

plexes, beginning with S

(= S) and ending with S

∞

(= DC ). A ﬁltration has O(n

) α-complexes since

there are O(n

) k-simplices, 0 ≤ k ≤3 (Seidel, 1995).

α-complexes for the protein 2JZC with 224 amino

acids and 3170 atoms and for selected values of α are

shown in Fig. 1.

Figure 1: α-complexes for the protein 2JZC with α =

1.5,2.0,3.0 and ∞.

As α grows, more and more simplices are in-

cluded in S

. A simplex σ

becomes a member of

when α = ρ

and b

is exposed. As α contin-

ues to grow, σ

can become a face of another sim-

plex (for example a triangle can become a face of a

tetrahedron). Later on, it can become an interior sim-

plex (for example a face of tetrahedron can become

a face of another tetrahedron). The α-values of these

events can be easily computed from the DC (Edels-

brunner et al., 1998). This is important since in many

applications one is not really interested in S

but in

AlphaComplexesinProteinStructurePrediction

179

the simplices on the boundary of S

. For a survey

of the applications of α-complexes to various protein-

related problems, see (Zhou and Yan, 2014; Winter

et al., 2009).

We make a simplifying assumption that all atoms

have the same size. Consequently, we focus on α-

complexes of points (or balls with the same radius).

Weighted α-complexes (Edelsbrunner and M

ucke,

1994) and β-complexes (Kim et al., 2006) for spheres

of different sizes have also been developed. However,

these more complicated structures require more com-

putational effort to be constructed and updated.

Consider an α-complex S

for some protein and

for a ﬁxed value of α, α > 0. S

can also be viewed

as an undirected graph G(α) with the vertices cor-

responding to the atom centers and the edges corre-

sponding to 1-simplices of S

. Since the lenghts of

covalent bonds in proteins are assumed to be ﬁxed and

are between 1

A and 1.5

A, G(α) will be connected al-

ready for α ≈ 0.80. For each vertex i, let N

(i) de-

note the vertices of G(α) that can be reached from

i by traversing at most d edges. Let N

∗

(i) denote the

subset of N

(i) containing vertices representing atoms

that are at least three covalent bonds away from i. Let

∗

= E

∗

+ E

∗

where

∗

∑

i∈G(α)

∑

j∈N

∗

(i)

i j

[

i j

]

−2e

i j

[

i j

]

)

and

∗

332

∑

i∈G(α)

∑

j∈N

∗

(i)

[

i j

]

We are interested in estimating relative errors

= |E

∗

−E

|/|E

and

= |E

∗

−E

|/|E

at different values of α and d.

4 IMPLEMENTATION

The applicability of α-complexes to the determina-

tion of potential energy of proteins was carried out as

follows. In the ﬁrst stage, 5 proteins (1X5R, 1X0O,

1XDX, 1AKP, 1Y6D) with 110-120 amino acids were

tested. This was done to verify the stability of the ap-

proach as well as to estimate the quality of the solu-

tions obtained. In the second stage, two bigger pro-

teins (2ZJC, 224 amino acids and 3WCZ, 308 amino

acids) were investigated to check if the approach re-

mains robust as the size of proteins increases.

The relative error ε

of the van der Waals contri-

butions to the potential energy of 1X0O remains the

same already for α > 1.6

A, d = 1,2, ...,5. Further-

more, ε

≈ 0%, d = 3,4,5 while ε

≈ 0.22% for

d = 2 and ε

≈ 1.86% for d = 1. Similar relative

errors were observed for the other four proteins with

110-120 amino acids. For the larger proteins 2JZC

and 3WCZ, ε

was also stable for α > 1.6

A. Fur-

thermore, for 2JZC, ε

≈ 0% for d = 3,4, 5 while

≈ 0.19% for d = 2 and ε

≈ 1.74% for d = 1.

For 3WCZ, ε

≈ 0% for d = 3,4, 5 while ε

≈

0.41% for d = 2 and ε

≈ 3.16% for d = 1.

Fig. 2 shows the relative error ε

of the Coulomb

contributions to the potential energy of 1X0O for the

values of α = 1.0, 1.1.,..., 5.9 . It can be seen that

≤2% already for α > 1.6

A and d = 3, 4,5. Also,

≤ 2.5% for d = 2. For d = 1 and α > 1.6,

≈ 6%. Similar relative errors were observed for

the other four smaller proteins with 110-120 amino

acids. For 2JZC with 224 amino acids, ε

≤ 1.5%

for α > 1.6 and for all d = 1,2, ...,5. It is perhaps

somewhat surprising that this was the case for d ≤ 2.

For 3WCZ with 308 amino acids, ε

≤ 1.5% for

α > 1.6 and d = 3,4, 5. For d = 2 and α > 1.6,

≤ 4% while for d = 1 and α > 1.6, ε

≤ 7%.

Fig. 3 shows the time (in ms) needed to compute

van der Waals and Coulomb contributions of non-

bonded atom pairs of 1X0O (using Mac OS X with

1.7 Ghz Intel Core i5 processor). The graph for d = 1

is not shown as it overlaps with the x-axis and is also

covered by the graph for d = 2. Similar computa-

tional times were observed for the other 4 proteins

with 110-120 amino acids. The computational time

does not include the construction of the α-complex

but it includes the determination of N

∗

(i) for each

vertex i. Not surprisingly, the computational time

increases with d as well as with α. However, for

d = 1 and α < 2

A, the computational time is below

2.1 ms. More interestingly, for d = 2 and α < 2

(where ε

and ε

are reasonably small), the com-

putational time is below 28 ms. For d = 3 and α < 2

the computational time is below 230 ms. For compar-

ison, computational time with cutoff = 8

A is below

27 ms, with cutoff = 20

A is below 52 ms, and with-

out cutoff is below 216 ms. Hence, picking d = 2 and

α ≈ 1.8

A seems to be a good choice when computing

nonbonded contributions to the potential energies of

protein conformations.

Computational times for 2JZC and 3WCZ are of

course higher. However, for d = 2 and α < 2

A, the

computational time for 2JZC is below 75 ms and it is

below 110-120 ms for 3WCZ.

BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

180

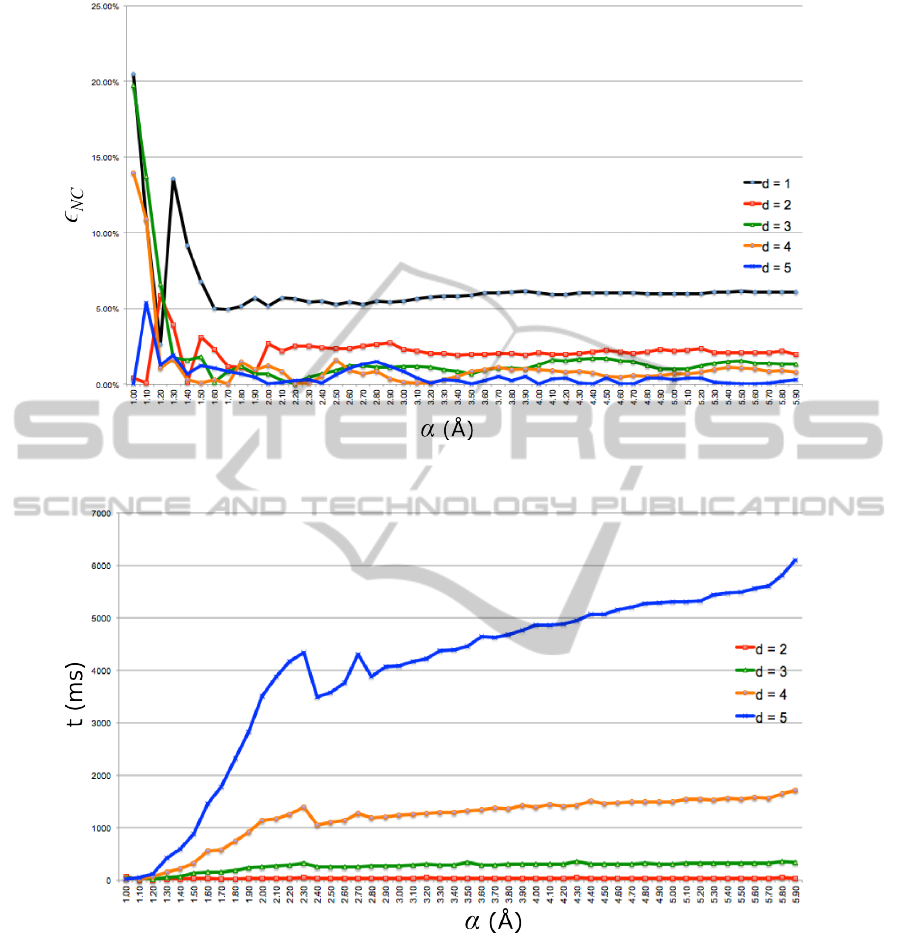
Figure 2: Relative errors for Coulomb interactions in 1X0O.

Figure 3: Computational times for 1X0O (in ms).

5 DISCUSSION

The results show that E

≈ E

∗

and E

≈ E

∗

for

various proteins, already for small d (= 2), and small

α (≈2

A). Hence, 2-complexes seem to provide a use-

ful discrete structure that can be used to speed-up the

determination of the potential energy of protein con-

ﬁgurations. This conclusion is of course only valid

if 2-complexes are given beforehand. Otherwise, the

determination of a 2-complexes with 2000 or more

atoms would be computationally much more expen-

sive than when the potential energy is determined by

any cutoff approach.

However, the use of 2-complexes in potential en-

ergy estimations deserves further investigation. In the

protein structure prediction, a vast number of possi-

ble protein conﬁgurations is examined when search-

ing for the native one minimizing the potential energy.

The search typically involves moving from one con-

ﬁguration to the next. One way to deﬁne neighbor-

AlphaComplexesinProteinStructurePrediction

181

hood of a conﬁguration is by dihedral rotations of one

or several covalent bonds by some, usually small, an-

gle. Atoms on one side of the rotating bond remain

stationary while the others rotate on orbits in parallel

planes and with centers on a common axis. Similarly,

if a covalent bond on a side chain is rotated, only a

very limited number of atoms on the side chain ro-

tates while all other atoms remain stationary.

Kinetic data structures for objects moving on

piecewise continuous trajectories are far from trivial.

The determination of how and when such data struc-

tures must be updated typically involves ﬁnding roots

of high-degree polynomials. For DC s, deciding when

a k-simplex T , k ≤ 3, becemes (seizes to be) Delau-

nay involves ﬁnding roots of polynomials of 8-th de-

gree (Russel, 2007). In α-complexes, it is necessary

to determine when a k-simplex T , k ≤ 3, becomes

(seizes to be) Gabriel and when it becomes (seizes to

be) short (Kerber and Edelsbrunner, 2013).

Fortunately, when rotating covalent bonds of pro-

teins, the computational effort of updating kinetic

data structures can be signiﬁcantly reduced. It can

be shown that kinetic DC s and kinetic α-complexes

for this kind of restricted and coordinated movement

of objects (with the same rotational velocity) involve

ﬁnding roots of polynomials of degree at most 4. Fur-

thermore, as the results presented in this paper indi-

cate, the depth d of a neighborhood N

∗

(i) of vertex i

does not need to be greater than 2 or 3. Hence, these

neighborhoods can be updated efﬁciently along with

the α-complexes.

In conclusion, α-complexes of proteins with rel-

atively low α do capture the potential energy contri-

butions of nonbonded atoms. Furthermore, kinetic α-

complexes for restricted types of motion can prove

useful in protein structure prediction when searching

through the vast atomic conﬁguration space.

REFERENCES

Edelsbrunner, H. (1992). Weighted alpha shapes. Univer-

sity of Illinois at Urbana-Champaign, Department of

Computer Science.

Edelsbrunner, H., Facello, M., and Liang, J. (1998). On the

deﬁnition and the construction of pockets in macro-

molecules. Discrete Applied Mathematics, 88(1):83–

102.

Edelsbrunner, H. and M

ucke, E. P. (1994). Three-

dimensional alpha shapes. ACM Transactions on

Graphics, 13(1):43–72.

Kerber, M. and Edelsbrunner, H. (2013). 3d kinetic al-

pha complexes and their implementation. In ALENEX,

pages 70–77. SIAM.

Kim, D.-S., Seo, J., Kim, D., Ryu, J., and Cho, C.-H.

(2006). Three-dimensional beta shapes. Computer-

Aided Design, 38(11):1179–1191.

Levitt, M., Hirshberg, M., Sharon, R., and Daggett, V.

(1995). Potential energy function and parameters for

simulations of the molecular dynamics of proteins and

nucleic acids in solution. Computer Physics Commu-

nications, 91(1):215–231.

Lotan, I., Schwarzer, F., Halperin, D., and Latombe, J.-

C. (2004). Algorithm and data structures for efﬁ-

cient energy maintenance during monte carlo simula-

tion of proteins. Journal of Computational Biology,

11(5):902–932.

Russel, D. (2007). Kinetic Data Structures in Practice. PhD

thesis, Stanford, CA, USA.

Schlick, T. (2010). Molecular Modeling and Simulation:

An Interdisciplinary Guide, volume 21. Springer.

Seidel, R. (1995). The upper bound theorem for polytopes:

an easy proof of its asymptotic version. Computa-

tional Geometry, 5(2):115–116.

Winter, P. and Fonseca, R. (2012). Adjustable chain

trees for proteins. Journal of Computational Biology,

19(1):83–99.

Winter, P., Sterner, H., and Sterner, P. (2009). Alpha shapes

and proteins. In ISVD’09. Sixth International Sympo-

sium on Voronoi Diagrams, pages 217–224. IEEE.

Zhou, W. and Yan, H. (2014). Alpha shape and delaunay

triangulation in studies of protein-related interactions.

Brieﬁngs in Bioinformatics, 15(1):54–64.

BIOINFORMATICS2015-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

182