Agents Displacement in Arbitrary Geometrical Spaces

An Evolutionary Computation based Approach

Francesco D’Aleo

, Fabio D'Asaro

, Valerio Perticone

, Giovanni Rizzo

and Marco Elio Tabacchi

1,2

Dip. di Matematica ed Informatica, Università degli Studi di Palermo, Palermo, Italy

Ed Istituto Nazionale di Ricerche Demopolis, Demopolis, Italy

Keywords: Agent-based Modeling, Optimization.

Abstract: In many different social contexts, communication allows a collective intelligence to emerge. However, a

correct way of exchanging information usually requires determined topological configurations of the agents

involved in the process. Such a configuration should take into account several parameters, e.g. agents

positioning, their proximity and time efficiency of communication. Our aim is to present an algorithm,

based on evolutionary programming, which optimizes agents placement on arbitrarily shaped areas. In order

to show its ability to deal with arbitrary bi-dimensional topologies, this algorithm has been tested on a set of

differently shaped areas that present concavities, convexities and obstacles. This approach can be extended

to deal with concrete cases, such as object localization in a delimited area.

1 INTRODUCTION

In an agent simulation, just as in real social contexts,

communication among individuals is one of those

characteristics that can enhance survival as well as

performances fitness-wise (Caci et al., 2011, Cardaci

et al., 2013, Tabacchi et al., 2010, Villata et al.,

2012). Communication allows a collective

intelligence to emerge, as it has been shown by

research on insects and using animat (Bonabeau et

al., 1999).

In many scenarios it is necessary to transmit

messages to a number of distinct intermediaries

(while other information can be delivered to many

agents at the same time using broadcast mode, Terna

& Taormina, 2007), due to the distance between

individuals. The concept of distance itself can be put

into question: in nature, distances are usually

regarded as “physical” distances, while in other

scenarios this concept can be readily extended; for

instance, consider the cost of a link between two

computers (Barabási, 2002), the energy cost of a

biological link between cells (Albert, 2005), or even

between concepts (Petrou et al., 2010). Further

problems can be caused by the presence of natural or

artificial obstacles between two individuals, or even

by a limited channel capacity.

In our proposed scenario, several agents inhabit

an arbitrarily shaped environment populated by

obstacles, and they can only communicate through

intermediaries lying at some maximal distance one

from another; each of such intermediaries is able to

receive messages from several sources and forward

them to other individuals in the designed area. This

is a broadcast kind of transmission: in order to reach

the destination, a single individual forwards the

received message to several intermediaries, ensuring

some desirable characteristics such as the robustness

and reliability of the ensuing network.

The number of agents in such a network is

usually variable, and it is necessary to consider the

possibility that some specific agents could reach a

huge number of other agents lying at a reasonable

distance, and at the same time to have a low number

of errors due to the transmission medium and to

episodes such as the temporary inactivation of an

agent or even its permanent removal from the

network. Therefore it is not out of place to draw an

analogy with social networks dynamics: in our case,

intermediaries behave just like hubs making possible

for distant nodes, which would otherwise have

difficulties to reach each other, to communicate.

A central parameter to consider, if we are to

assess the network evolution in time, is the

minimum number of agents needed to reach every

agent in the network; finding an optimal value

without introducing errors or noise in the signal is a

198

D’Aleo F., D’Asaro F., Perticone V., Rizzo G. and Elio Tabacchi M..

Agents Displacement in Arbitrary Geometrical Spaces - An Evolutionary Computation based Approach.

DOI: 10.5220/0005230601980202

In Proceedings of the International Conference on Agents and Artiﬁcial Intelligence (ICAART-2015), pages 198-202

ISBN: 978-989-758-073-4

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

notoriously hard problem (Tabacchi & Termini,

2011). On the other hand, if we consider the network

arrangement in space, the topology of the

environment – that is, the absolute (with respect to

space) and relative (with respect to other agents)

position of each agent – has to be carefully taken

into account. Optimal and sub-optimal solutions to

well-known and highly idealized situations are

already available in literature, including Steiner’s

Tree (Hwang et al., 1992); however, it is harder to

deal with harsher, possibly non-convex, non-

contiguous, and/or arbitrarily complex areas.

In these cases, a soft-computing technique

(Seising and Tabacchi, 2013) such as evolutionary

programming (Michalewicz, 1996) could provide

sub-optimal solutions in a reasonable amount of

time. Evolutionary algorithms in general, and

especially genetic algorithms, are already

successfully applied to a huge number of

optimization problems and they are proven of being

capable to efficiently find “good” solutions, i.e.

solutions that closely approximate the best one.

In this work we propose a preliminary version of

an evolutionary algorithm, which serves to optimize

the number and position of agents in arbitrarily

shaped areas, possibly populated by obstacles.

Results have shown how the algorithm satisfies sub-

optimality criteria as well as strong connectivity

requirements and were also obtained in an efficient

way. Even more, the algorithm tries to optimize the

number of agents, removing the superabundant ones

from the map.

This article is organized as follows: in the next

section we shall describe in detail the problem we

are concerned with and the approach we chose to

face it. In the third section we shall present the

algorithm as we implemented it, while analyzing the

principal mechanisms regulating agents and entities

of the simulation. Last section is devoted to

conclusions and to possible further developments of

this work. Some alternative methodologies and

different approaches to this very problem are

discussed and it will be pointed out how this work

can be applied to problems of a very different nature

than the one considered here.

2 METHODOLOGY

In the study and analysis of an ideal network, it is

crucial to focus on the first stages of its creation,

since the initial topology can have a severe impact

on network functionalities and evolution, as well as

on its principal entities, i.e. those nodes establishing

interconnections among peers.

Amongst the fundamental aspects to be

considered we should mention the minimization of

the number of entities involved in the peer-

communication process, which plays an important

role during the construction stage. In fact, an

excessive number of agents can lead to some

inconveniences (already well-known in information

theory) such as information redundancy and

corruption due to signal degradation. However,

decreasing the number of entities should not

compromise the connection between them —

therefore it turns out to be indispensable to evaluate

the proportion between number of nodes and

available space.

Another point that should be carefully taken into

account is that network topology could contemplate

the presence of hubs, which play a fundamental role

for the reasons discussed in the introduction;

however, the number of hubs in a network should

not exceed a critical limit, since otherwise we would

get an inefficient network due to the redundancy of

some connections.

Some mathematical models to deal with

canonically shaped areas are already known in

literature; they allow to find the “best” (with regard

to communication efficiency and total number of

entities) way of positioning entities in such highly

idealized scenarios, though this formally restricts the

possible choices by presenting characteristics that

are not modifiable by those entities moving in the

arbitrarily shaped spaces.

Considering all the limits and problems arising in

such situations, it comes as no surprise that finding

the optimal solution is a computationally unfeasible

problem. However, we can find suboptimal solutions

in a reasonable amount of time using evolutionary

programming techniques. In particular, in the next

section we shall introduce and discuss a procedure

that employs an evolutionary algorithm augmented

by hill-climbing, of which many variants are

available.

Even though a full detailed description of the

algorithm is the focus of the next chapter, we want

to highlight that the algorithm plays a crucial role

because of its capacity of satisfying all the requisites

mentioned before. This very algorithm acts as a

leader, imposing a direction for the entities to move,

without asking them to act in a precise way. The

leader also evaluates the solution at each stage of the

process, using a fitness function, which is based on

an evaluation of the total area covered by each

agent.

Some motivation for the leader to be

AgentsDisplacementinArbitraryGeometricalSpaces-AnEvolutionaryComputationbasedApproach

199

implemented through a genetic algorithm comes

from the fact that similar approaches were already

successfully used in various areas such as wire

routing, scheduling, adaptive control, game playing,

cognitive modeling, transportation problems,

traveling salesman problems, optimal control

problems, database query optimization (for a review

see Michalewicz, 1996).

Single agents, on the other hand, are

implemented through the already mentioned hill-

climbing algorithm, that is, a greedy algorithm

which at each iteration chooses the best state,

leading every time to a better (or, at least, non-

worse) solution.

Unlike a gradient-descending technique, we

chose the possibility of introducing a tabu search

variant to avoid repeated actions.

3 ALGORITHM

The idea behind our algorithm is to initially set up

the map in a way derived from the optimal solution

for a canonical shape surrounding the area we are

considering. For such shapes we can indeed use

some well known algorithms about Convex Hull

problem in a bi-dimensional plane. Such algorithms

are based on several differential and computational

geometry theorems (Vazirani, 2001). In particular,

Groemer’s theorem (Groemer, 1960) establishes a

relation between an area and the number of nodes

that are needed to cover (compact or convex) parts

of it. However, efficient algorithms in the more

general case of non-convex, non-compact areas are

not known.

In this work, the “optimal solution” is considered

as a starting point from which it is then possible to

calculate, through refinements, the desired sub-

optimal solution for the real area in consideration.

The refining procedure consists of moving the

agents in every possible way in a pre-defined

neighborhood, while verifying whether the new

placements leads to an improvement of the general

connectivity status. More precisely, agents are able

to move in their neighborhood according to a turn-

based mechanism.

At each turn the leader, which cannot be

identified with any agent and which therefore

constitutes an external entity, evaluates whether it is

necessary to order a movement or not. Such

broadcast communication forces all the agents to

make a displacement, providing them useful

information about their neighborhood.

It should be carefully noticed that in some

Table 1: Highlights of the algorithm.

1. Set up the agents in a way derived from the

optimal solution, as suggested by Groemer’s

Theorem;

2. Moving the agents in every possible way in a

pre-defined neighborhood and recalculate the

fitness function;

3. Repeat step two until find the sub-optimal

solution. Any configurations loop are avoided

using the tabu search;

4. Remove one of the agents and recalculate the

fitness function;

5. Repeat step four until find a configuration with a

fitness function better or worse, however, not

more than a certain tolerance (5%) compared to

the solution of the previous iteration.

situations the presence of an agent could turn out to

be redundant; these superabundant agents should be

removed from the map, since every such agent bears

a cost.

Our leader can take into consideration this

important factor by progressively removing

redundant components, i.e. those that carry no

significantly contribution to the improvement of the

global solution. The "greedy" procedure described in

steps 4—5 is clearly order-dependent since the order

in which the antennas are sequentially taken off

might affect the final result. In fact, we could

perform an exhaustive (hence, order-independent)

search of the optimal set of antennas to be removed

instead. However, such a process would be

unfeasible computationally wise, while our "greedy"

procedure, even though order-dependent, is more

efficient and approximates the theoretical optimum

with sufficient precision. The presence of a leader

provides the possibility of reducing the network’s

size without having to care about conflicts between

agents and/or spontaneous deletion of single nodes.

The main parameters involved in this

computation are: the initial distance between agents,

the minimum distance allowed between different

agents, the size of the neighborhood. These

parameters are set at the beginning of the simulation

and remain fixed during the entire execution of the

procedure. The leader only considers the first of

these three variables, while the latter two are

broadcasted to each single agent.

Simulation halts whenever the leader stops

communicating relevant information to the agents.

Such process is asynchronous due to the indirect

nature of the communication. Once this

organizational process is over, agents can go on

exchanging information in an efficient way,

expPloiting the new optimized network topology

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

200

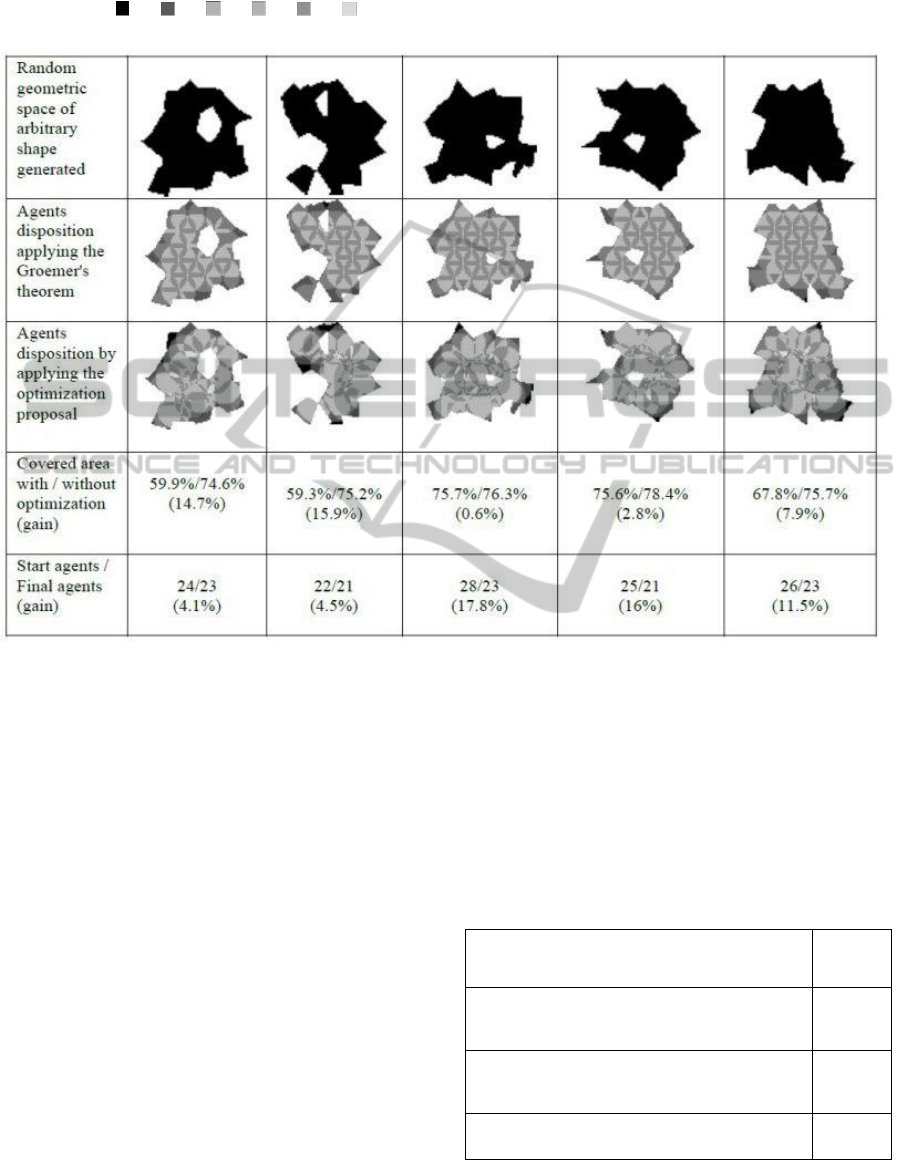
Table 2: Results obtained from pseudo-random generated samples. In the second row the area covered by agents is shown

using Groemer’s Theorem. Each grey level represents the number of agents covering the underlying area, according to the

following scale: =0, =1, =2, =3, =4, =5 or more. In the third row the disposition of agents after optimization is

shown.

4 CONCLUSIONS

A first collection of tests carried out in a simulated

environment confirmed the soundness of our

algorithm. This reinforces the hypothesis about the

validity of abstract mathematical models when they

are applied to social areas such as information

exchange.

If a suitable set of parameters is chosen, this

approach can be readily extended to other fields, e.g.

object localization in a three-dimensional

environment.

Further developments of this work could

contemplate the possibility of putting aside the

leader and making single agents independent. In this

case they will be free to decide action timing and to

start/resolve conflicts to eliminate superfluous

agents. Obviously this would lead to a new set of

(computational) issues related to the observance of

global constraints, which however might be

conveniently handled through information exchange

between agents.

Furthermore, fuzzy sets theory can be fruitfully

applied to this framework by using a suitable

membership function wherever required (D’Asaro et

al., 2013a, D’Asaro et al., 2013b). In this way, it is

possible to find a suitable solution even when an

external constraint prevents the fitness function from

being maximized.

Table 3: Aggregated results from a pseudo-random

generated sample.

Sample

N =

1.000

Average (Standard Deviation) of the

coverage for 3 or more agents using the

Groemer’s theorem

62.29%

(8.53%)

Average (Standard Deviation) of the

coverage for 3 or more agents using the

algorithm proposed

71.17%

(5.94%)

Average (Standard Deviation) of the number

of removed agents

10.82%

(5.66%)

AgentsDisplacementinArbitraryGeometricalSpaces-AnEvolutionaryComputationbasedApproach

201

REFERENCES

Albert, R. (2005). Scale-free networks in cell biology.

Journal of cell science, 118(21):4947–4957.

Barabási, A. L. (2002). Linked: The New Science of

Networks. Basic Books.

Bonabeau, E., Dorigo, M., Theraulaz, G. (1999). Swarm

intelligence. Oxford.

Caci, B., Cardaci, M., Tabacchi, M. E. (2011). Facebook:

topology to personality and back – an actor-based

simulation. In Kokinov, B., Karmiloff-Smith, A., and

Nersessian, N. (eds.) European Perspectives on

Cognitive Science. New Bulgarian University Press.

Cardaci, M., Fiordispina, M., Perticone, V., Tabacchi,

M.E. (2013). Reti sociali, informazioni individuali.

Una simulazione basata su agenti, metodologia fuzzy e

Computing With Words. In Auricchio A., Cruciani

M., Rega A., Villani M. (eds.) Atti del Convegno

AISC 2013, pp. 71—77.

D'Asaro, F. A., Perticone, V., & Tabacchi, M. E. (2013a,

August). A fuzzy methodology to alleviate

information overload in eLearning. In 8th conference

of the European Society for Fuzzy Logic and

Technology (EUSFLAT-13). Atlantis Press.

D'Asaro, F. A., Perticone, V., Tabacchi, M. E., & Termini,

S. (2013b). Reflections on Technology and Human

Sciences: rediscovering a common thread through the

analysis of a few epistemological features of

fuzziness. Archives for the Philosophy and History of

Soft Computing, (1).

Groemer, H. (1960). Über die einlagerung von kreisen in

einen konvexen bereich. Mathematische Zeitschrift,

73(3):285–294.

Hwang, F., Richards, D., and Winter, P. (1992). The

Steiner Tree Problem. Annals of Discrete

Mathematics. Elsevier Science.

Michalewicz, Z. (1996). Genetic algorithms + data

structures = evolution programs. Springer.

Petrou, M., Tabacchi, M. E., Piroddi, R. (2010). Networks

of Concepts and Ideas. The Computer Journal,

53(10):1738--1751.

Russell, S., Norvig, P. (2010). Artificial Intelligence: A

Modern Approach. Prentice-Hall.

Seising, R., Tabacchi, M. E. (2013). A very brief history

of soft computing. In Pedrycz, W. and Reformat, M.

(eds.) 2013 Joint IFSA World Congress NAFIPS

Annual Meeting. IEEE SMC.

Tabacchi, M. E., Caci, B., Cardaci, M. (2010).

Comportamenti individuali e connettivi in Facebook:

uno studio simulativo. In Ferrari, G., Bouquet, P.,

Cruciani, M., and Giardini, F. (eds.) Pratiche della

Cognizione - Atti del Settimo Convegno Nazionale di

Scienze Cognitive, pp. 266--270. AISC.

Tabacchi, M. E., Termini, S. (2011). Measures of

fuzziness and information: some challenges from

reflections on aesthetic experience. In Proceedings of

WConSC 2011.

Terna, P., Taormina, R. (2007). Modelli di simulazione

con agenti intelligenti: il sorprendente mondo dei

camaleonti. In Sistemi Intelligenti, vol. 19, pp. 391--

426. Il Mulino.

Vazirani, V. V. (2001). Approximation algorithms.

Springer.

Villata, S., Falcone, R., Da Costa Pereira, C.,

Castelfranchi, C., Tettamanzi, A., Paglieri F. (2012).

Comunicazione e fiducia: un modello ad agenti su

qualità delle informazioni e valutazione delle fonti. In

Paglieri, F. (ed.) Sistemi Intelligenti, vol. 24, pp. 559--

579. Il Mulino.

ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence

202