Empirical Models as a Basis for Synthesis of Large Spiking Neural

Networks with Pre-Specified Properties

Mikhail Kiselev

Department of Applied Mathematics, Chuvash State University, Universitetskaya 38/1, Cheboxary, Russia

Keywords: Spiking Neural Network, Empirical Model, Dynamic Threshold, Short Term Synaptic Depression, Decision

Tree, Multiple Adaptive Regression Splines.

Abstract: Analysis of behaviour of large neuronal ensembles using mean-field equations and similar approaches was

an important instrument in theory of spiking neural networks during almost all its history. However, it often

implies dealing with complex systems of integro-differential equations which are very hard not only for

obtaining explicit analytical solution but also for simpler tasks like stability analysis. Building empirical

models on the basis of experimental data gathered in process of simulation of small size networks is

considered in the paper as a practical alternative to these traditional methods. A methodology for creation

and verification of such models using decision trees, multiple adaptive regression splines and other data

mining algorithms is discussed. This idea is illustrated by the two examples – prediction of probability of

avalanche-like excitation growth in the network and analysis of conditions necessary for development of

strong firing frequency oscillations.

1 INTRODUCTION

At present, large spiking neural networks (SNN)

(Gerstner and Kistler, 2002) are considered not only

as plausible models of neuronal ensembles in

various sections of mammalian brain but also as a

technological basis for creation of intelligent robots,

learnable automated control systems, biometric and

multimedia processing devices as well as for many

other breakthrough technologies of near future.

Probably, even in this decade it will be possible to

build computational systems capable of real time

simulating populations of 10

– 10

(or even 10

)

neurons that is close to size of human brain. At least,

the ambitious all-European Human Brain Project

declares it as one of its main targets. Impressive

advances of neuromorphic hardware (Monroe, 2014)

(see, for example, the SpiNNaker project

http://apt.cs.manchester.ac.uk/projects/SpiNNaker/)

also make believe that it is quite realistic. However,

availability of these powerful computers with

massive parallelism is only necessary but not

sufficient condition. It would be unreasonable to

expect that building huge neural network with

certain (even biologically realistic) parameters and

pressing the button “Start” we will observe some

desired or interesting (or even simply non-trivial)

network behaviour. Therefore, the second crucial

and still unsolved problem is synthesis of network

with required characteristics for realization on these

future super-parallel computers. Since these

networks are very big, the exact specification of

their detailed structure is absolutely impossible.

Instead, only general statistics determining

distribution of synaptic weights, delays, interneuron

connection probabilities and other structural

properties of network as a whole will be specified,

while exact detailed network configuration will be

generated randomly accordingly to these distribution

laws. Therefore, the discussed problem can be

formulated as follows. How, knowing parameters of

the neuron model used, the distribution laws of

network structural characteristics and the general

properties of input signal, could we predict

properties of the whole network in terms of neuron

firing frequency, firing correlations, reaction to input

signal variation and other values determining target

behaviour of the network? This problem is very

difficult even for simplest neuron models and

completely homogenous networks.

The most popular approach to its solution is

based on mean-field equations (Baladron et al.,

2012). Undoubtedly, the mean-field approach has

264

Kiselev M..

Empirical Models as a Basis for Synthesis of Large Spiking Neural Networks with Pre-Speciﬁed Properties.

DOI: 10.5220/0005134102640269

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 264-269

ISBN: 978-989-758-054-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

proven to be a valuable tool for theoretical analysis

of correlated and chaotic network activity, stability

and other large-scale network properties. However,

in my opinion, its application to the above

mentioned problem will be very limited for the

following reasons:

 Even for relatively simple neuron models the

mean-field equations may take form of system

of complex integro-differential equations, which

cannot be solved analytically (for example,

when synaptic delays are non-zero and vary

from synapse to synapse). Although their

general solution is not required for some

purposes (e. g. for stability analysis) in most

cases it has to be obtained by numeric methods.

 The mean-field approach is based on the

assumptions which are often unrealistic. It is

assumed that number of neurons is infinite. But

consequences of network size finiteness, so

called finite size effects, may be very significant

even for large networks making estimations

obtained by classic mean-field equations

imprecise (Touboul & Ermentrout, 2011). There

are other situations violating basic conditions

for application of this method – for example,

presence of numerous small populations of

neurons with highly correlated activity like in

Izhikevich’s models of neural information

processing and memory based on

polychronization effect (Izhikevich, 2006).

 As a rule, creation and analysis of mean-field

equations require substantial research efforts. In

fact, it is a small (or even large) research project

in every case. A minor complication of explored

problem – say, addition of some correlations in

originally Poisson external signal may lead to

dramatic complication of the equations

analyzed. If demand for this kind of study will

be great then much simpler alternative methods

will be required.

The main idea of this paper is that the basic

instrument for creation of networks with specified

required parameters should be empirical models –

formulae expressing dependences of the parameters

describing network activity (the output parameters)

on the variables controlled by network designers –

such as number of excitatory and inhibitory neurons

and synapses, constants in distribution laws for

synaptic weights and delays, individual neuron

parameters etc. (the input parameters). These models

are obtained as a result of automated analysis of

experimental data by data mining algorithms. It is

assumed that the routine semi-automated procedure

for finding these empirical dependences should

include the following steps:

1. Determination of input and output parameters

which could enter the sought models. For the input

parameters it is also necessary to set their possible

variation ranges. The input parameters should not

include extensive variables directly depending on

network size. For example, percent of inhibitory

neurons should be used instead of absolute number

of inhibitory neurons. It is necessary in order to

make the built models scalable.

2. Performing experiments with moderate size

networks and various combinations of the input

parameter values. Number of these experiments

should be sufficient to cover all interesting regions

of the input parameter space and to avoid possible

model overfitting. The good starting point for this

choice is the rule that number of experiments should

be at least 2 orders of magnitude greater than

number of model degrees of freedom. The very

important factor is size of networks used in these

experiments. Since many interesting processes in

SNNs are statistical by their nature it is senseless to

experiment with small networks and expect that the

obtained results will be valid for large SNNs as well.

On the other side, the network should be much

smaller than the target simulated network –

otherwise the whole process would not make sense.

Probably, networks consisting of thousands neurons

would be a good trade-off in many cases. Input

parameter values in these experiments can be set in

accordance with various strategies – random setting,

placement on a grid and so on.

3. Analysis of the tables consisting of input

parameter values and corresponding output

parameter magnitudes measured in the experiments.

It can be done using various data mining algorithms

– this step is considered in next sections.

4. Model scalability verification. Even in case

when the models do not include variables directly

depending on network size, it may be that size of

networks used in these experiments series is

insufficient to reveal important statistical effects or

causes too strong fluctuations distorting the

dependencies sought. In order to test model

scalability a limited number of experiments with

larger networks should be carried out.

This scheme has a number of obvious

advantages. It is semi-automatic and can be

routinely used for a great variety of network

architectures, input signals etc., it produces the

results in the explicit analytical form which can be

used for further analysis (possible by means of

symbolic math software because the found empirical

EmpiricalModelsasaBasisforSynthesisofLargeSpikingNeuralNetworkswithPre-SpecifiedProperties

265

formulae may be huge). Besides, in many cases the

found dependencies can be interpreted by a

researcher and can improve her or his intuitive

understanding of the processes in SNNs.

In the rest of the paper I present an example of

application of this methodology for solution of the

following quite general problem. It is natural that

SNNs performing different functions should behave

differently. However there are at least 3 network

behavior patterns which are useless in any situation:

complete silence – when neurons do not fire at all;

spike avalanche – when firing frequency

demonstrates explosive growth to its maximum

possible level; and strong global oscillations – when

(almost) all neurons fire inside short time intervals

separated by periods of (almost) complete silence.

Our task is to find conditions under which network

has good chances to avoid these negative scenarios

and, therefore, has a chance to demonstrate some

non-trivial reaction to external signal.

2 LIF NEURON WITH DYNAMIC

THRESHOLD AND

SHORT-TERM SYNAPTIC

DEPRESSION

At first, let us consider the neuron model used in this

study. It is a simple generalization of the commonly

used leaky integrate-and-fire (LIF) neuron model. It

has two additional features, whose purpose is to help

keeping firing frequency in necessary limits. These

are dynamic threshold (Benda et al, 2010) and short-

term synaptic depression (Rosenbaum et al., 2012)

(although, I utilize a simpler realization of this

mechanism than models considered there and in

many other works). This model has efficient

computational realization due to its simplicity but

can reproduce many interesting non-linear effects. I

have been used the similar neuron models in several

simulation experiments (Kiselev, 2009, 2011)

however include here only its short formal

description because it is used only for illustration of

the proposed idea.

Neuron state includes two components: dynamic

part of threshold

)0( hh and contributions of

individual synapses to current membrane potential

value

v ( niv



 1,10 , where n is the total

number of synapses). If we denote weight of ith

synapse as w

then the actual value of membrane

potential can be written as





vwu . Membrane

potential is rescaled so that its rest value equals to 0

while the firing threshold value after long period of

inactivity is taken equal to 1. Beside

, neuron

properties are described by the two time constants:



and



- the time constants of exponential decay

h and

v , respectively.

Thus, neuron dynamics obeys the rules:



 , ;



v when the ith synapse receives spike;

hvw





1 the neuron fires and

0,1 





vhh .

(1)

We see that effect of a presynaptic spike received

by the synapse on membrane potential is less than w

if the same synapse received a presynaptic spike

recently. All synapses are non-plastic.

3 NETWORK

We study completely homogenous and chaotic

network consisting of excitatory and inhibitory

neurons. Their amounts always correspond to the

ratio 10:3 – relative strength of excitation and

inhibition in the network is controlled by

modification of numbers of excitatory and inhibitory

synapses and their weights. All excitatory (E) and

inhibitory (I) neurons have the same parameters.

Thus, there are 4 kinds of synapses:

IIEIIEEE  ,,,

. Every excitatory

neuron has the same number of EE and IE synapses.

The similar rule is valid for inhibitory neurons. All

synapses of the same type have the same weight.

Synaptic delays are distributed randomly using

lognormal distribution with standard deviation of

logarithm of delay equal to 1. Excitatory

connections are slow (mean delay = 5 msec) while

inhibitory connections are much faster (mean delay

= 1.5 msec) – it is known that inhibitory connections

are really faster in the brain. Set of presynaptic

neurons is absolutely random for every neuron in the

network.

Thus, the network is characterized by the twelve

parameters: the time constants

vIvEhIhE



,,, , the

numbers of synapses n

, n

, and the

synaptic weights w

, w

4 EXTERNAL SIGNAL

We explore the situation when network receives

pure Poisson external signal. Its source is a set of

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

266

network input nodes emitting spikes with certain

constant mean frequency uniform for all input

nodes. All excitatory neurons are connected to

randomly selected subsets of input nodes via

excitatory synapses (we will call them afferent

synapses). We set number of the afferent synapses

equal to 30 in all experiments – we vary the total

external stimulation strength using the mean external

signal frequency.

5 GOAL: AVOIDING NEGATIVE

SCENARIOS

The preliminary experiments show that if all the

parameters are set randomly then with great

probability one of the three things happens: network

does not react on stimulation at all; neurons begin

firing with maximum possible frequency; “zebra-

like” activity when network switches between short

periods of collective hyperactivity and periods of

almost complete silence. The network cannot

perform any useful task in any of these states so that

our aim is to find the conditions when they are

impossible or at least unlikely.

Avoiding the first situation is easy – it is only a

question of sufficient stimulation strength so that let

us consider the 2

one. We will study satisfaction of

the stronger condition, namely, it is required that

network reaction to any stimulation would either

fade away completely after stimulation end or return

to certain not very high baseline firing frequency

level – let it be 30Hz. To test it the experiments are

designed in the following way. The network

received the constant stimulation during some time

interval which was significantly longer than any of

vEhIhE



,, or



. After that the external signal is

switched off and network activity is monitored

during next long interval. If the mean firing

frequency in this period does not exceed 30 Hz (for

any value of stimulation strength) then the network

is declared as “good” or belonging to the class

Otherwise, it belongs to the class

Situation with super-strong oscillations is not so

evident because firing frequency oscillation strength

can be evaluated in many different ways. I chose the

following measure (which will be referred to as

Relative Oscillation Strength – ROS).

1. For every discrete time step t the number of

emitted spikes F(t) is fixed.

2. The autocorrelation function A(t) is calculated

for F(t).

3. Let T be the least value of t for which A(t)

becomes negative. Then the dominating oscillation

period T

OSC

corresponds to maximum of A(t) on

),(



T .

4. Assume that the total experiment time equals

to nT

OSC

, where n is integer. Then, the function







OSC

iTtFtC

)()(

is calculated for 0 < t <

OSC

5. The interval (0, T

OSC

) is broken to 10 equal

parts; the mean values of C(t) are calculated in each

of these 10 parts. If the minimum of these 10 values

is c

min

, and the maximum is c

max

, then ROS = (c

max

min

) / c

max

Thus, we have the two problems to solve:

 to classify a network to S

or, better, to

evaluate conditional probability P(A|

) that

for the given vector of input parameters A the

network belongs to

;

 to predict its ROS value.

6 MAIN SERIES OF

EXPERIMENTS

I performed main series of experiments with

networks consisting of 1000 excitatory neurons and

300 inhibitory neurons. The input parameters were

varied in the following ranges: 3 – 100 msec – for all

time constants, 10 – 300 – for number of excitatory

synapses, 3 – 100 - for number of inhibitory

synapses, 0.03 – 0.3 – for weights of excitatory

synapses, 0.1 – 10 - for weights of inhibitory

synapses. Values of stimulation intensity and

afferent synapse weights were selected to satisfy the

requirement that mean firing frequency of isolated

neuron should lay in the range 2 – 300 Hz.

The stimulation duration was 3 sec that is at least

30 times greater than any neuron time constant.

Network activity was also monitored during next 3

sec after stimulation end – in order to place the

network in class

or S

. Also, ROS value was

calculated in every experiment.

The whole series contained 202332 experiments

– it took about 1 day of computation on a powerful

multi-core PC. 27572 different combinations of

network parameters were tested for different

stimulation intensity values.

EmpiricalModelsasaBasisforSynthesisofLargeSpikingNeuralNetworkswithPre-SpecifiedProperties

267

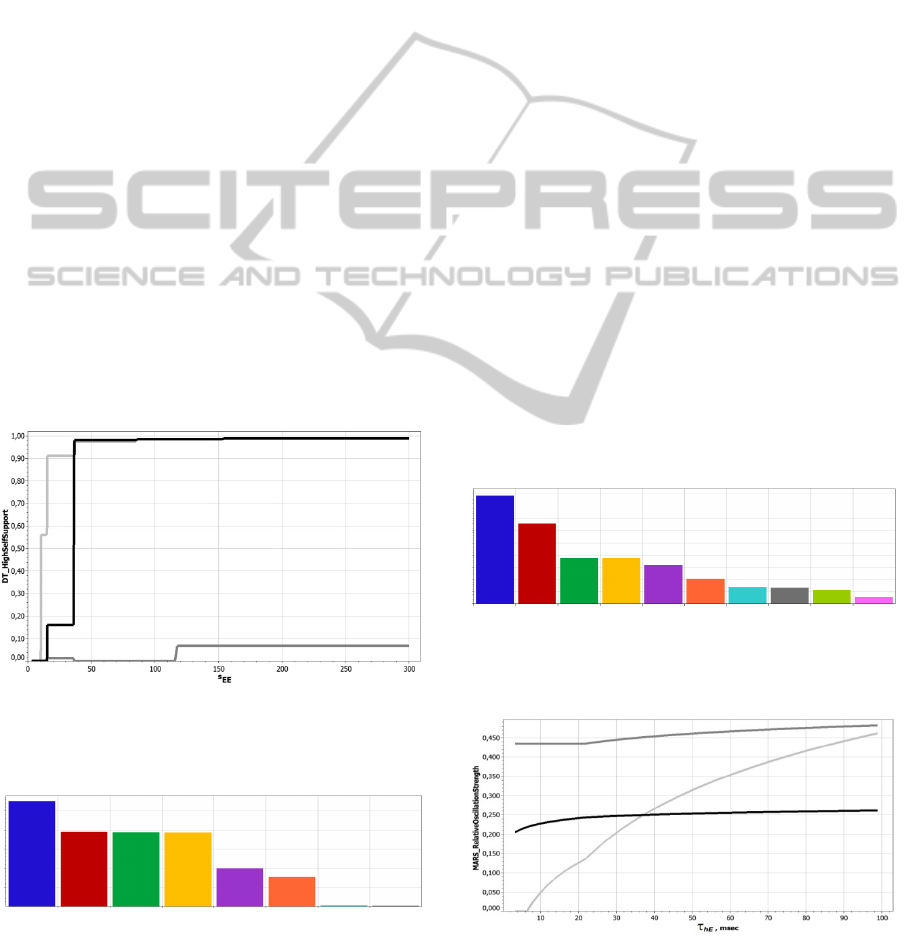
7 CREATION OF EMPIRICAL

MODELS

7.1 S

Classification

Thus, we have 27572 training cases, 9255 of them

belong to

. Since the result should obviously

depend on total strength of excitation and inhibition

in the network, the following useful derivative

parameters

ABABAB

wns  are produced, where A

and B belong to {E, I}.

Having experimented with different

classification methods I discovered that the best

results are obtained by one of the most popular data

mining algorithms, decision tree. I tested only those

methods which are able to represent their results in

an explicit analytical form – for this reason, such

methods as support vector machines or neural

networks were not considered. The resulting tree-

like classification model has 105 non-terminal nodes

and gives 7.21% classification error. It is important

that decision tree can also estimate P(A|

Examples of its dependence on the strength of

positive feedback in the network for 3 different

combinations of other parameters are depicted on

Figure 1. The good model quality is illustrated by

the sharp transition of this probability from 0 to 1.

Figure 1: Examples of dependence of P(A| S

) on strength

of positive feedback in the network for 3 different

combinations of its other parameters.



Figure 2: Relative importance of network parameters for

its classification into S

or S

The model can be represented in symbolic form or

as C code (they can be obtained from me by

request). Moreover, the used implementation of

decision tree algorithm is able to evaluate the

relative influence of different network parameters on

classification result. It is presented in form of

histogram on Figure 2.

7.2 ROS Value Prediction

This time we had to use data mining algorithms

finding numeric interdependencies. In this case the

multiple adaptive regression splines algorithm

(Friedman, 1991) was found to be a champion

among all methods which express obtained model in

a symbolic form. This algorithm represents found

dependence in form of piecewise continuous

polynomials. In our case the built model includes 59

degrees of freedom. Its accuracy estimation

(standard deviation = 0.28, R

= 0.45) is not very

impressive. Nevertheless, it happened to be quite

useful. For example, the condition ROS < 0.1

guarantees with high probability that time course of

firing intensity in the network will not take form of

strong oscillations. Similar to decision tree, the

considered algorithm evaluates relative contributions

of independent variables. They are shown on Figure

3. Examples of dependence of ROS on the main

factor,



, for various combinations of other

factors are displayed on Figure 4.



Figure 3: Relative contribution of network parameters in

ROS value prediction model variability.

Figure 4: Examples of dependency of ROS value on



for various combinations of other network parameters.

NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications

268

8 SCALABILITY TEST

Since the created models do not contain explicitly

absolute amounts of excitatory and inhibitory

neurons, it is reasonable to hope that their results

may be valid for much larger networks.

As a practical criterion to classify a network to

I use the rule that decision tree estimation of P(A|

) should not exceed 0.3. For small networks (1300

neurons) it gives about 3% of errors. This rule was

tested on 114 10 times greater networks with

combinations of parameters randomly selected in

accordance with the same distribution laws but

retaining only the networks satisfying this criterion.

Surprisingly, none of these networks belonged to

Probably, the greater accuracy of this classification

rule for larger networks can be explained by lower

relative magnitude of statistical fluctuations.

The situation with ROS value prediction is

similar. From my experience I selected critical value

of ROS equal to 0.3. For small networks 15% of

parameter combinations with predicted ROS less

than 0.3 show real value of ROS greater than 0.3.

This error for the greater networks drops to 10.5%.

Although the performed tests may be

insufficient, they can be considered as evidence that

empirical models obtained for smaller size networks

may be at least equally accurate for larger ones and

possibly even more accurate due to weaker impact

of statistical fluctuations.

9 CONCLUSIONS

By the present paper I would like to remind

researchers working in the field of SNN simulation

that empirical models obtained from experiments

with small size networks can be a valuable tool for

design, analysis and monitoring of large (and even

huge) SNNs realized on massively parallel

supercomputers. The term “monitoring” is used here

in relation to the stability problems typical for many

synaptic plasticity models. For example, it is known

that STDP mechanism can easily lead network to an

uncontrolled hyperactivity state because of its

inherent positive feedback. In this case, the

parameters calculated on the basis of empirical

models could signal that network is approaching the

dangerous regions.

This approach is a practical alternative to

complicated theoretical analysis based on mean-field

equations because these equations (also being only

more or less realistic approximation) often take form

of complex integro-differential equations excluding

possibility of their analytical solution. Attractiveness

of the proposed methodology is especially evident in

circumstances when great number of various

network models in combination with changing

external signal properties should be analysed in a

limited time.

The typical strategy of creation of such models is

considered in the paper and illustrated by simple but

practically applicable examples. The reported

empirical dependences were found using

PolyAnalyst™ data mining system developed by

Megaputer Intelligence Ltd.

REFERENCES

Gerstner, W., Kistler, W., 2002. Spiking Neuron Models.

Single Neurons, Populations, Plasticity. Cambridge

University Press.

Monroe, D., 2014. Neuromorphic computing gets ready

for the (really) big time. Communications of the ACM,

57 (6): 13–15. doi:10.1145/2601069.

Baladron, J., Fasoli, D., Faugeras, O., and Touboul, J.,

2012. Mean-field description and propagation of chaos

in networks of Hodgkin-Huxley and FitzHugh-

Nagumo neurons. The Journal of Mathematical

Neuroscience, 2:10 doi:10.1186/2190-8567-2-10.

Touboul, J., Ermentrout, G., 2011 Finite-size and

correlation-induced effects in mean-field dynamics.

Journal of Computational Neuroscience 31 (3): 453-

484. DOI:10.1007/s10827-011-0320-5.

Izhikevich, E. 2006. Polychronization: Computation With

Spikes. Neural Computation, 18: 245-282.

Benda, J., Maler, L., Longtin, A. 2010. Linear versus

nonlinear signal transmission in neuron models with

adaptation currents or dynamic thresholds. Journal of

Neurophysiology. 104: 2806-2820.

Rosenbaum, R., Rubin, J., Doiron, B. 2012. Short Term

Synaptic Depression Imposes a Frequency Dependent

Filter on Synaptic Information Transfer. PLoS Comput

Biol 8(6): e1002557. doi:10.1371/journal.pcbi.

1002557.

Kiselev, M. 2009. Self-organized Spiking Neural Network

Recognizing Phase/Frequency Correlations. In

Proceedings of IJCNN’2009, Atlanta, Georgia, 1633-

1639.

Kiselev, M. 2011. Self-organized Short-Term Memory

Mechanism in Spiking Neural Network. In

Proceedings of ICANNGA 2011 Part I, Ljubljana,

120-129.

Friedman, J. 1991. Multivariate Adaptive Regression

Splines. Annals of Statistics. 19(1): 1-141.

EmpiricalModelsasaBasisforSynthesisofLargeSpikingNeuralNetworkswithPre-SpecifiedProperties

269