
Neuron Dynamics of Two-compartment Traub Model
for Hardware-based Emulation
Juan Carlos Moctezuma
1,2
, Jose Luis Nunez-Yanez
2
and Joseph P. McGeehan
1
1
CCR Group, Electronic Engineering, University of Bristol, Bristol, U.K.
2
Micro Group, Electronic Engineering & Computer Science, University of Bristol, Bristol, U.K.
Keywords: Traub Model, Pinsky-rinzel Model, Bursting Analysis, Firing Analysis, Two-compartment Models, Neuron
Modelling, Biophysically Accurate Hardware-model.
Abstract: The two-compartment Pinsky and Rinzel version of the Traub model offers a suitable solution for hardware-
based emulation, since it has a good trade-off between biophysical accuracy and computational resources.
Many applications based on conductance-based models require a proper characterization of the neuron
behaviour in terms of its parameters, such as tuning firing parameters, changing parameters during learning
processes, replication and analysis of neuron recordings, etc. This work presents a study of the dynamics of
such model especially suitable for hardware-based development. The morphology of the neuron is taken
into account while the analysis focuses primarily on the relation between the firing/bursting properties and
the relevant parameters of the model, such as current applied and morphology of the cell. Two different
applied currents were considered: short duration and long steady. Seven different types of burst patterns
were detected and analysed. The transformation process of the membrane voltage when a long steady
current varies was classified into five stages. Finally, examples of neuron recording replication using the
present methodology are developed.
1 INTRODUCTION
Learning and memory process in any neuron or
neural network is based on activity-dependant
neuron responses. Modification of the physiological
parameters is the tool to understand the functional
and behavioural significance of this process; such
parameters can modify patterns of neuronal
firing/bursting and affect the behaviour in more
high level functions (Dayan and Abbott 2001). For
instance, several learning techniques and algorithms
have been studied to achieve this goal and all of
them are based on the modification of parameters in
order to modify the neuron response (Grzywacz and
Burgi 1998; Dayan and Abbott 2001).
Conductance-based modelling is not the
exception, knowing the effects on the dynamics in
the neuron is crucial to have control in the bursting
and firing signals; which at the end, is the
information that neurons will share through the
system. Moreover, parameter’s control in
conductance-based model plays an important role in
exploring the biological properties and dynamics
mechanisms in real neurons or in the development of
control systems that lead to new feedback electrical
stimulation for neural prostheses applications (Jiang
et al. 2005; Fei et al. 2006).
The conductance-based models incorporate
cellular detail at ion-channel level dynamics; this
allows model biologically realistic neurons. One of
the most important features of these models is that
they are biophysical compatible and hence
neuroscientists, biologists, psychologists can, at
certain level, study the properties and co-relate
directly parameters with their biological
counterparts.
One of the most used conductance-based models,
besides the well know Hodgkin-Huxley (H-H)
(Hodgkin and Huxley 1952) is the Traub model
(Traub et al. 1991) and its simplify two-
compartment version P-R (Pinsky and Rinzel 1995),
which take into account information about calcium
ion channel Ca
2+
. Calcium dynamic is another
important element in the chemical and electrical
behaviour in the neuron. This model can reproduce
some burst patterns that H-H model cannot (Zhang
et al. 2010). The two-compartment model includes
two parts: a soma-like, which has the Na
+
and K
+
85
Carlos Moctezuma J., Luis Nunez-Yanez J. and P. McGeehan J..
Neuron Dynamics of Two-compartment Traub Model for Hardware-based Emulation.
DOI: 10.5220/0005089500850093
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2014), pages 85-93
ISBN: 978-989-758-054-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

activated currents; and a distal dendrite-like, where
Ca
2+
activated and potassium Ca
2+
-dependent
currents are considered.
This research focus on the study of dynamic
behaviour for the two-compartment P-R model with
morphology information included. Most works
related with this topic use theoretical and continuous
model; however a hardware-based discrete model is
not considered. Since our primary investigation is to
develop biophysically compatible neuro-simulators
and their hardware realization, it is important to keep
good performance in order to have biological
compatibility and reproduce consistent results from
real nervous systems.
2 REVIEW OF PREVIOUS WORK
In this section, we review previous work done
related to dynamic analysis in conductance-based
models, particularly those using the Traub model.
Studies of firing and bursting mechanisms in
biological neurons have been widely studied during
many years. Nerve cells can generate a variety of
firing patterns in vivo, where repetitive burst, fast
spikes, low frequency spikes, large calcium spikes,
d-spikes, etc. have been recorded (Schwartzkroin
1975; Traub 1982).
In the original work of the P-R model (Pinsky
and Rinzel 1995), an intrinsic bursting analysis
when current is applied and excitatory synaptic
interactions effect was performed. Another similar
work is a piece-wise analysis where P-R model is
separated in different stages and a dynamics study
including burst initiation and somatic-dendrite ping
pong is done (Coombes and Bressloff 2005). This
work performs several reductions to the original
model in order to make a phase-plane examination.
Bifurcation analysis is also a very useful
approach to analyse dynamics in a neuron model as
the parameters vary. Several works have studied this
topic mainly for the well-known Hodgkin-Huxley
model, in such works oscillations, stability in
systems, bursting properties, spikes generation,
temperature has been explored on this model (Rinzel
and Miller 1980; Guckenheimer and Labouriau
1993; Wang et al. 2005; Fei et al. 2006). The
bifurcation analysis becomes more difficult when
the nonlinear systems have more than two
parameters and equations to be considered at the
same time.
The effect of the size in the soma in P-R model is
studied and shows that the smaller the soma is, the
faster and the more irregularly the neuron fires
(Feng and Li 2001). A modified version of the P-R
model in order to have just two parameters variables
in each compartment’s equation is studied when
capacitance changes and how complex bursting are
generated (Kepecs and Wang 2000; Wang et al.
2012).
Several works using biological-compatible
models have been developed in order to mimic real
nervous systems behaviour; from study of single
complex neurons to mimic complete biological
systems (Khan and Miller 2010; Smaragdos et al.
2014). These researches highlight the importance of
using this kind of models.
One important detail about previous work based
on the P-R model is that the morphological
properties are reduced to a simple parameter p,
which indicates the proportion of the cell membrane
area taken up by the soma. In the present work we
extend this information by representing soma and
dendrite as cylinder compartments where radius,
length and axial resistivity are taken into account.
Traub model has been widely used in a variety of
contexts, but little analysis has been performed for
models of hardware-based applications and using the
conductance-based approach.
3 THE P-R TRAUB MODEL FOR
HARDWARE EMULATION
The P-R model is used in this work. This model
offers a suitable trade-off between biophysical
accuracy and computational feasibility to be
developed in hardware (Zhang et al. 2010).
3.1 Specific Compartment Model
The cable equation and the multi-compartment
theory describe the voltage change with respect to
both variables: time and space. In the cable equation
a segment of cell membrane is represented as a
cylinder (cable); taking into consideration six
currents: the capacitive
; the total ionic-channels
; the injected
; and two more currents coming
from adjacent segments
and
(Bower and
Beeman 1998; Dayan and Abbott 2001). In this way,
the cell membrane equation can be defined in terms
of temporal and spatial variables t and x:
1
2 ∙
∙
(1)
Where
and
are the specific axial resistivity
in unit of K-cm and the specific membrane
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
86

capacitance in unit of µF/cm
2
respectively.
and
are the applied and ionic channel currents per unit
area expressed in µA/cm
2
. The cylindrical segment
(compartment) having radius a and length dx=Δx (in
units of cm) provides the morphological
information. V is the membrane voltage in mV.
Because we need to represent this in a digital and
computational way, the membrane voltage must be
integrated numerically; to address this issue multi-
compartment approach is used. Also, in order to
reduce the PDE system to an ODE system, which is
more suitable for numerical computation, the second
order derivative in equation (1) is approximated by
the discrete derivative version using the Taylor
series expansion (Bower and Beeman 1998).
Equation (2) shows a generic representation of the
cell membrane for an arbitrary compartment j, where
right compartment and left compartment are
represented by j+1 and j-1 respectively.
′
2
∆
2
(2)
Note that
can represent either soma or dendrite
compartment. Each one has its own ionic-channel
current
, with Na
+
and K
+
ionic current
components for soma and Ca
2+
, K
+
_AHP, K
+
_C
current components for dendrite. Remind, every
compartment has its own morphological dimensions.
A complete description and specific variable values
of the ionic-channel currents and the
opening/closing rate functions and can be found
on (Pinsky and Rinzel 1995).
3.2 Numerical Method Solution
Because the model used for this work is intended to
work in digital programming devices a numerical
solution is needed. In (Zhang et al. 2010) it is shown
that the best solution is the backward-Euler method,
since it can maintain system stability regardless of
the system structure and parameter selection.
However this method brings high computational
cost. The exponential-Euler method becomes
unstable when the number of compartments
increases or when a special combination of
parameters is used, but it is more feasible in terms of
hardware development. Since the model proposed
has only two compartments and because just specific
unusual combination of parameters cases makes the
system unstable, exponential Euler method is the
best option to implement.
Rewriting the cell equation (2) in a more
convenient way:
∗
∗
Where,
2
∆
∗
B
∆
(3)
Where
,
are the weighted averages of
all ionic channels conductances. These two terms
change according to the type of compartment (soma,
dendrite or synapse); for instance, both terms for
soma compartment are:
∙
∙
_
∙
and
∙
∙∙
_
∙∙
∙
.
Applying exponential-Euler solution to equation
(3), we can obtain the explicit solution for next time
step given by equation (4):
∗
∗/
(4)
3.3 Hardware Platform
A system on chip (SoC) platform has been been
developed where neuroprocessors form single or
two-compartment neurons and control the
connection between them. Such neuro-modules
follow a scheme of state machines controllers
(FSMCs), floating-point arithmetic units (FPALUs)
and BRAMs to store internal results. Also, each
neuroprocessor has associated a dual-port RAM
(DRAM) in order to configure and control relevant
parameters such as maximum conductance, input
current, ions equilibrium potentials, geometric
parameters, time step, configuration of state
variables, etc. A neuroprocessor can be configured
as a soma, dendrite or synapse compartment. For the
purpose of this study a soma and dendrite
neuroprocessor are used.
Figure 1: SoC system reconfigurable architecture.
NeuronDynamicsofTwo-compartmentTraubModelforHardware-basedEmulation
87

The control and data paths are formed by a number
of configurable FSMCs and FPALUs, respectively.
The FSMCs are devised to fetch operands or
forward computation results between the FPALUs
and their associated RAMs. All temporary variables
are saved in these internal memories that are located
at the input ports of the FPALUs (Zhang et al. 2010;
Moctezuma et al. 2013)
This platform is FPGA-based using an embedded
microprocessor which is in charge of the control and
communication task. In addition, there is a software
firmware running which is able to manage the
configuration of the neuroprocessors and make
interconnections among them. This firmware is
continuously receiving instructions from a
MATLAB script running on a PC. Then commands
can be send to configure the neuroprocessors, start a
simulation and request results.
4 DYNAMICS ANALYSIS AND
RESULTS
The dynamics analysis is divided into several stages,
all of them related with the configuration of the
neuron when current applied and geometric
parameters change.
Following this scheme; the analysis is separated
in four scenarios: burst classification; tuning the
bursting neuron at resting state; short and long
steady current applied and the impact of geometric
dimensions. For all experiments, unless otherwise
stated, the axial resistivity is 100 K-cm, the
diameters for soma and dendrite are 86.6 µm and 5
µm, respectively. The length of the cylindrical
dendrite is set to 15 µm, these values are consistent
with measured experiments on hippocampal
pyramidal cells (Traub 1982; Traub et al. 1994;
Zhang et al. 2010).
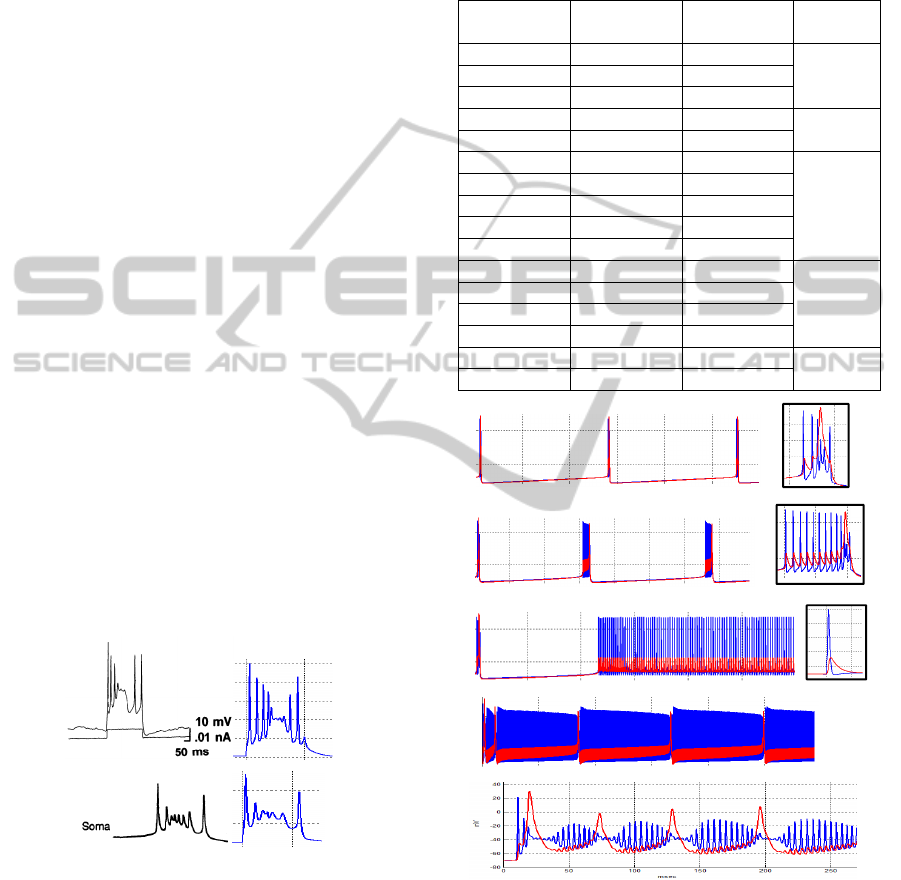
4.1 Soma-Burst Classification
In order to understand and discern the neuron
outputs in soma compartment, we have proposed
seven different types of bursts for classification.
Some of these bursts can be found also in biological
experiments from neuron recordings (Traub 1982;
Traub et al. 1991; Traub et al. 1994; Booth and Bose
2002). Figure 2 shows this classification.
Next, we defined each type of burst and explain
their properties.
SP: Single Spike. SP2: Single main spike followed
by other peaks. Normally they are sequences of two,
three, or four spikes. Dendrite main wide-spike is
not well defined. BA: Classic Traub-burst, with
initial sodium spike, followed by set of smooth
oscillations during main dendrite wide-spike and
ending with a final spike during the AHP current
phase. Normally it has from two to four peaks. BA2:
A Traub-burst shape with several pikes before the
maximum of dendrite spike. Normally it has more
than two spikes. The wide dendrite main spike starts
to define. BC: Similar to SP2 but with a dendrite
wide-spike defined. Normally it has 3 spikes. BC2:
Collection of sequenced spikes but a little bump on a
spike or small wide-pike is present. The main
dendrite wide-spike is defined. BD: Classic Traub-
burst shape, but with two principal set of spikes at
the beginning and at the end enclosing the central
part, which oscillates smoothly.
SP SP2 BC
BA2 BA BD
BC2
Figure 2: Burst classification with traces of soma (blue)
and dendrite (red) compartments. Burst duration 20
msec.
4.2 Tuning Non-bursting at Resting
State
The Traub-based model has a particular property
that when no stimulus is applied to the cell
membrane the neuron undergoes periodic bursting,
albeit with very low frequency (Pinsky and Rinzel
1995) of around 0.6 Hz. However, this can be an
undesirable behaviour when a learning process is
involved; since normally, if a neuron is at its resting
state, we do not expect the neuron to fire. To
overcome this issue without affecting significantly
the neuron dynamics, there are two options: to apply
a large steady negative current or to slightly tune the
leakage conductance. Table 1 shows the results
obtained.
We found that a current of
= -0.85 µA/cm
2
is
enough to maintain the neuron at its resting state of -
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
88
70mV without firing. When current is bigger (more
negative) than -1.7 µA/cm
2
then resting potential
tends to move away to less than -75mV.
The second option is reduce the leakage
conductance. The original work of Pinsky-Rinsel
and Traub, set a value of
=0.3; table 1 shows that a
slightly reduction of
at a value of 0.285 mS/cm
2
is
enough to eliminate the bursting and keep the resting
potential close to -70 mV. Moreover, if we decrease
leakage conductance below 0.28 mS/cm
2
the resting
potential moves away to -75 mV. In conclusion
leakage conductance is highly sensitive to changes,
but a value of 0.285 can overcome the initial
bursting issue at the resting state without
compromising the dynamic of the neuron.
Table 1: Current applied and leakage conductance tuning
to eliminate initial bursting at resting stage.
Parameter Value Bursting V
rest
(mV)
(µA/cm
2
)
> -0.85
[-77 -70]
-0.85 - -71
-1.00 - -72
< -1.70 - < -75
(mS/cm
2
)
0.3
[-78 -70]
> 0.3
0.285 - -72
0.28 - -74
< 0.28 - < -75
4.3 Short and Long Steady Current
Applied
In this section, we focus on finding the minimum
stimulus needed to generate a single burst in the
neuron, and how this short current modifies the
quality of bursting in terms of outcome spikes. The
second goal is to measure the outcomes from a long
and steady current applied and determine the relation
with the bursting behaviour of the neuron.
4.3.1 Short Current Applied
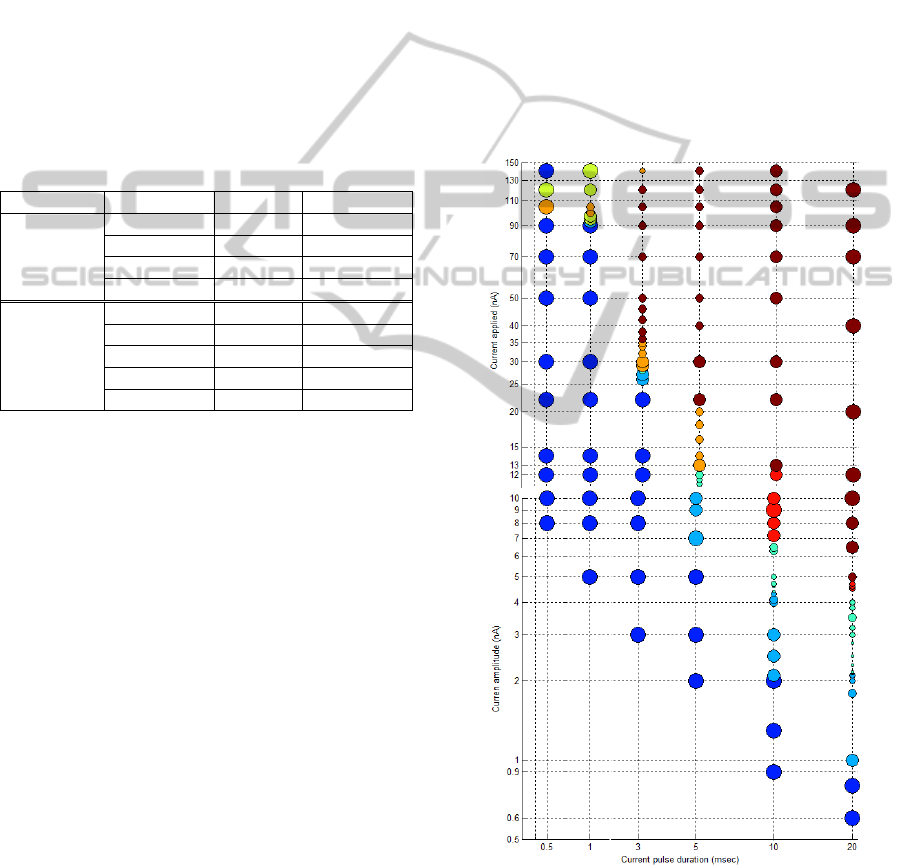
The minimum short applied current needed to
generate a single spike is 8 nA (136 µA/cm
2
) with a
duration of 0.5 msec, see figure 3. With this
duration, a current in the order of mA/cm
2
per unit
area in order to have a proper Traub bursting patron,
however the spike amplitude overtakes 150 mV,
which is not common amplitude for spikes. So the
duration of 0.5 msec for the applied current is
enough just to generate single spike but not Traub
bursts such BA or BD type.
However if we increase the pulse duration, then
the minimum applied current to generate a single
spike is shorter; for instance, with a 20 msec current
pulse, it is necessary a 0.6 nA current to generate a
SP spike. Hence if want a neuron to fire only single
spikes then a pulse duration between 0.5 and 3 msec
is ideal, see figure 3.
Following the same procedure, we run several
experiments varying both current pulse duration and
amplitude. Figure 3 shows the results obtained with
the properties explained.
Another important characteristic about this
model is that in order to have Traub-burst shapes
like BA, BA2 or BD type, the current applied should
last more than 3 msec and a range of [2 15]nA
should be used; and the larger the pulse is, the
current applied becomes more “fine-grained”
(narrow) as pulse duration increases, e.g. when pulse
Figure 3: Soma membrane voltage response to different
current pulse duration and amplitude. The colour in circles
indicates the type of burst. The circle size indicates the
number of spikes, where biggest blue circle is a single
spike, followed by less big circles with 2 or 3 spikes; then
medium size circles have a range of [4 6]; and smallest
circles have between 7 and 10 spikes.
NeuronDynamicsofTwo-compartmentTraubModelforHardware-basedEmulation
89
duration is 20 msec, in order to have complex traub
burst, a current between 4.4 and 4.7 nA is needed.
The duration of a Traub-burst when a current
pulse is applied normally is about 20 msec. When a
longer pulse is used then the burst duration takes the
time that the pulse does. Also, we found that the
current needs to be applied at least for 10 or 20 msec
if we are interested in neuron fires between 5-10
times in the 20 msec window that the burst lasts.
Also we notice that there is an evolution pattern
for this model. This evolution can be described by
the following sequence: SPSP2BA2/BCBA/
BDBC2. It starts with a single spike, then as the
current increases, it generates two or three more
spikes and the dendrite acts as passive. After that the
dendrite starts to produce a main wide-spike caused
by the ping-pong effect between the two
compartments and a series of spikes are generated in
the rising edge of the dendrite wide-spike. If we
continue to increment the current, then the classic
Traub-burst appears; but there is a point where this
burst loses it shape due to a big current applied to
component
dominates the equation and the neuron
dynamic results in a first sodium spike followed by
a smooth steady level of voltage.
These results can be applied to generate
replicated behaviour for biological neurons
recordings or to explore the neuron dynamics in a
well-controlled environment. As an example
consider two neuron output recordings from (Traub
et al. 1991; Traub et al. 1994) works compared with
the output from our model (figure 4). Using results
from figure 3, the neuron behaviour can be
controlled and analyse in a practical way.
Figure 4: Burst replication of biological neuron recordings
(left) with the two-compartment model proposed (right).
4.3.2 Long Steady Current Applied
Now we consider a long steady current applied
during the whole simulation. When a constant
current drives the neuron, spikes frequency appears
rather than single burst patterns.
A set of experiments were developed varying
current amplitude and principal stages of the process
as shown in figure 5. Meanwhile table 2 shows the
relation of current vs frequency and stage
transitions.
Table 2: Spike trains frequency and stages transition
according to figure 4.
(nA)
Freq (Hz) Spikes in
Burst
Stage
0.0156 0.21 3
A
0.020 0.26 3
0.035 0.34 3
0.080 0.57 7
B
0.087 0.57 10
0.087007 [50-41] 1
C
0.20 [33-58] 1
0.60 [76-90] 1
0.90 [100-111] 1
1.20 [110-125] 1
1.40 [112-130] 1
D
1.80 [112-140] 1
2.50 [140-160] 1
4.00 [200-250] 1
4.50 80 1
E
5.00 0 0
A
B
C
D
E
Figure 5: Different stages for a neuron soma (blue) and
dendrite (red) response when steady current increase.
Small left box indicates type of burst.
We distinguish five different stages according to
the current increment. Stage A fires Traub-burst at
very low frequency (VLF); in stage B the Traub-
burst are preceded by several single spikes at VLF as
well. There is a point at Ie=0.087007 nA where this
VLF burst disappears and a delayed spike train
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
90
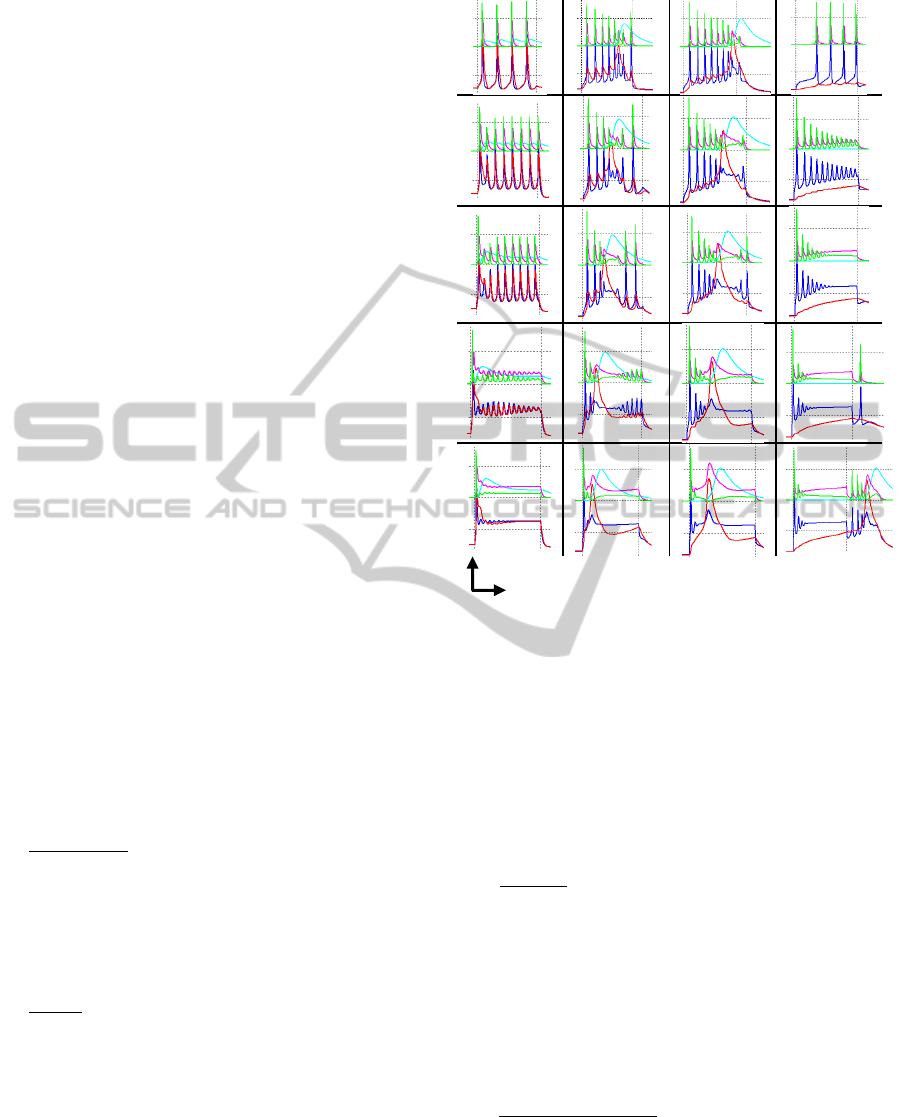
appears (stage C), this spike train approaches the
time of zero as current increases, at this stage we can
have frequencies between 50 and 110 Hz (see table
2).
Then when the spike train reaches time zero, a
low frequency envelope pattern is created, we can
appreciate better this behaviour on dendrite output
(red line) on figure 5-stage D; at this stage,
frequencies of 250 Hz can be achieved. The
amplitude of membrane voltage is reduced,
decreasing the spikes frequency. In addition, the low
frequency envelope pattern becomes more obvious
(figure 5-stageE top). Finally the neuron output
tends to become steady and the spike train
disappears at Ie=5nA (figure 5-stageE bottom).
The minimum and maximum frequencies
achieved with this model are 0.21 and 250 Hz
respectively. And there is a cut current of 0.087 nA
where traub-burst disappears and single spikes
emerge.
4.4 Effects of Geometric Properties
In this section we analyse the effects produced by
changes in geometric properties of soma and
dendrite. There are two main geometric parameters
which affect the membrane voltage according to
equation 3: the radius a and length ∆. Normally the
soma has a sphere shape (∆) and dendrite has a
cylinder form.
We took a well-defined Traub-burst type BD and
analyze the changes appreciated when soma radius a
and dendrite length ∆ vary. Figure 6 shows the
results and specifications for every trace.
There are four main effects when these two
parameters vary:
Attenuation. There is a general tendency of
attenuation in the soma output as radius
decreases; however on a dendrite output this
effect is not so obvious for some cases. A
major attenuation in the last part of neuron
response is presented as dendrite length
increases
Delay. The bigger soma radius or dendrite
length, the bigger delay for calcium
concentration. In addition, we can observe how
the number of pre-spikes or post-spikes are
modified as this concentration moves during
the 50 msec window. When both parameters
are too big, there is a point when the dendrite
output “disappears” (top-right figure 6), this
effect is because the dendrite response is so
delayed than the current pulse duration is not
long enough to obtain such response.
Figure 6: Different burst responses for a current pulse of
1.7 nA and 50 msec duration. Parameter values increase
from bottom to top and from left to right directions. Range
for radius soma a and dendrite length x are [15 60] and
[5 50] µm respectively. Soma (blue) and dendrite (red)
voltages in mV units. Calcium concentration (cyan),
sodium current (green) and potassium-rectifier current
(pink) in µA/cm
2
are attenuated by factor of 10
–1
. The
dendrite radius has a constant value of 3.6 µm, since it is
the parameter that changes the less. Every dashed square
represents 50 units x 50 msec.
Spiking. Normally the number of spikes
increases more when the soma radius is bigger;
also the dendrite wide-peak affects the number
of pre-spikes and post-spikes change. This last
consequence is related to the calcium
concentration shifting. In addition, as the
length of dendrite is smaller and the soma
radius becomes bigger, then dendrite gets
passive properties (top-left figure 6), active
properties appear when the length increases.
Change in currents. When soma radius is small
then K+ rectifier current is bigger than Na+
one. However when the radius becomes bigger,
then the current rules change. Because Na+
current is higher this causes the spiking effect
to produces more spikes as well.
a
x Parameter increment direction
NeuronDynamicsofTwo-compartmentTraubModelforHardware-basedEmulation
91
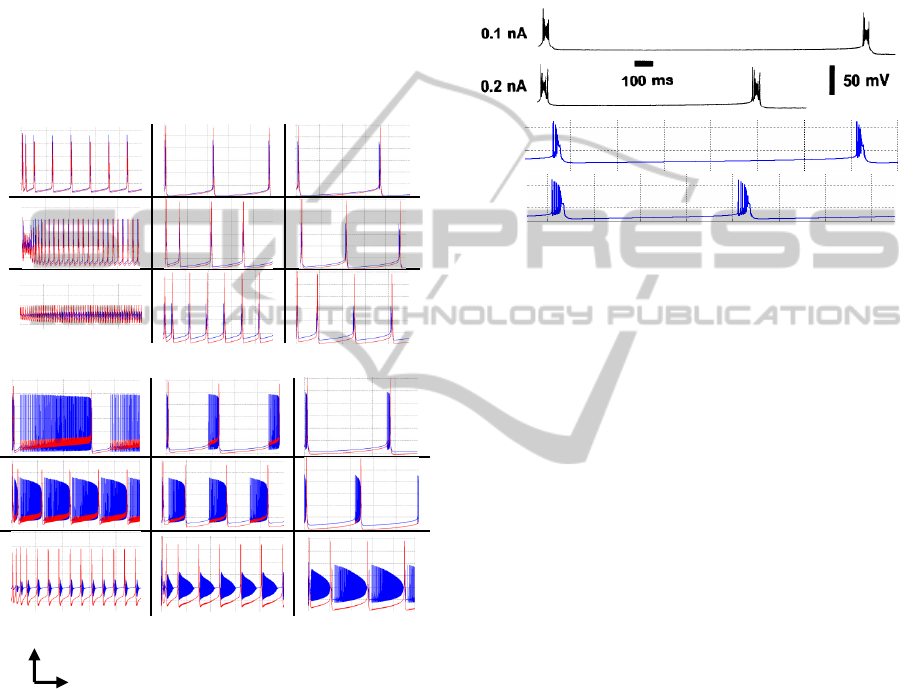
In order to analyse the morphological variation when
a long steady current is applied, we set up two
constant currents and vary soma radius and dendrite
length. Again the dendrite radius compartment
remains constant with a value of 2.5
µm. The
outcomes of the experiment are shown in figure 7.
For membrane voltage firing at VLF range, e.g.
stage A or stage B (figure 7-a), the morphological
parameters a-soma and
x-dendrite have influence
on the frequency and amplitude of the neuron
output. Decrementing the dendrite length raises
frequency; meanwhile decrementing the soma radius
reduces the soma amplitude.
a) 0.1 nA
b) 0.5 nA
Figure 7: Soma (blue) and dendrite (red) traces responses
for a long steady current of a) 0.1nA and b) 0.5nA.
Parameter values increase from bottom to top and from
left to right directions. Ranges for radius soma a are: a)[5
23] and b) [10 45] µm. Ranges for dendrite length x are:
a)[10 30] and b)[10 50] µm . Every dashed square
represents 20 mV x 500 msec.
When neuron fires in higher frequencies, e.g.
stages C and D (figure 7-b), the effect is still the
same, i.e. the bigger thee radius the less the
amplitude and the bigger the length, the less the
frequency. In addition we can control the generation
of periodic bursts, changing the number of spikes
per burst according to morphological parameters
tuning.
As an example consider the two recorded traces
in figure 8 taken from a CA3 neuron (Traub et al.
1991) for two different currents. The two-
compartment model was simulated with the same
current values. The output of the proposed model is
consistent with the recording value when the next
morphological parameters are considered: a-soma=
23.3
µm, a-dendrite=2.5 µm and x-dendrite=20 µm.
0.1 nA
0.2 nA
Figure 8: Burst replication of biological neuron recordings
(top) with the two-compartment model proposed (bottom).
Dashed square on simulation represents 50mVx 200 msec.
5 CONCLUSIONS
A detail dynamics analysis for the two-compartment
Traub model was developed, taking into
consideration that this model is used in hardware-
based applications. So the numerical method and
data representation must be taken into account, in
contrast with previous analysis which use software-
based PC simulators and where these
implementations details are not considered.
The presented hardware-based model is able to
reproduce biological meaningful information,
dynamic behaviour and it is suitable to reproduce
neuron recording experiments.
The leakage conductance and current applied can
be used to tune neuron to a non-bursting resting
state. Both options were selected because they do
not compromise the dynamics of the original model.
Through the analysis, two different applied
currents were considered: short duration and long
steady. For a short duration current, seven different
types of burst patterns were detected and analysed.
Also, it was detected that the transformation of such
bursts follows a specific sequence of patterns.
When a long steady current vary, the modification
of the membrane voltage trace was classified in five
different stages; where VLF burst, single periodic
spikes, low frequency periodic burst and modulated
single spikes can be generated with particular set of
values. Also it was found that geometric parameters
a
x Parameter increment direction
NCTA2014-InternationalConferenceonNeuralComputationTheoryandApplications
92

can influence in frequency and amplitude of neuron
response.
Specific parameters values of current applied and
morphological dimensions can be used to generate
different burst patterns or to move from one stage to
another when a specific firing frequency is required.
As future work, it is intended to use this
information for parameter self-tuning genetic
algorithm experiments and replicate living cells
recordings and study the influence of biological-
compatible parameters. In addition, dynamics
analysis will be extended to other parameters,
mainly to ion-channel maximum conductances and
inhibitory/excitatory synapses, in order to use this
information in a conductance-based neural network
learning algorithm.
The final goal is to build biophysically compatible
neurons that fit on single chips and have biological
meaningful information that matches behaviour of
real cells, in order to biologist have alternative ways
to study physical nervous systems in a configurable,
well-controlled and real-time environment.
REFERENCES
Booth, V. and A. Bose (2002). "Burst synchrony patterns
in hippocampal pyramidal cell model networks."
Network 13(2): 157-177.
Bower, J. M. and D. Beeman (1998). "The book of
GENESIS." Springer-Verlag New York, Inc.
Coombes, S. and P. C. Bressloff (2005). Bursting The
Genesis of Rhythm in the Nervous System, world
Scientific Printers.
Dayan, P. and L. F. Abbott (2001). Theoretical
neuroscience: computational and mathematical
modeling of neural systems, MIT.
Fei, X. Y., Jiangwang and L. Q. Chen (2006). "Bifurcation
control of Hodgkin-Huxley model of nerve system."
WCICA 2006: Sixth World Congress on Intelligent
Control and Automation, Vols 1-12, 9406-9410.
Feng, J. F. and G. B. Li (2001). "Behaviour of two-
compartment models." Neurocomputing 38: 205-211.
Grzywacz, N. M. and P.-Y. Burgi (1998). "Toward a
Biophysically Plausible Bidirectional Hebbian Rule."
Neural Computation 10(3): 499-520.
Guckenheimer, J. and I. S. Labouriau (1993). "Bifurcation
of the Hodgkin and Huxley Equations - a New Twist."
Bulletin of Mathematical Biology 55(5): 937-952.
Hodgkin, A. L. and A. F. Huxley (1952). "A quantitative
description of membrane current and its application to
conduction and excitation in nerve." J Physiol 117(4):
500-544.
Jiang, W., G. Jianming and F. Xiangyang (2005). "Two-
parameter Hopf bifurcation in the Hodgkin-Huxley
model." Chaos, Solitons & Fractals 23: 973-980.
Kepecs, A. and X. J. Wang (2000). "Analysis of complex
bursting in cortical pyramidal neuron models."
Neurocomputing 32: 181-187.
Khan, G. M. and J. F. Miller (2010). "Learning Games
using a Single Developmental Neuron." Proc. of the
Alife XII Conference(University of York).
Moctezuma, J. C., J. P. McGeehan and J. L. Nunez-Yanez
(2013). Numerically efficient and biophysically
accurate neuroprocessing platform. Reconfigurable
Computing and FPGAs (ReConFig), 2013.
Pinsky, P. F. and J. Rinzel (1995). "Intrinsic and network
rhythmogenesis in a reduced Traub model for Ca3
neurons." Journal of Computational Neuroscience
2(3): 275-275.
Rinzel, J. and R. N. Miller (1980). "Numerical-Calculation
of Stable and Unstable Periodic-Solutions to the
Hodgkin-Huxley Equations." Mathematical
Biosciences 49(1-2): 27-59.
Schwartzkroin, P. A. (1975). "Characteristics of CA1
neurons recorded intracellularly in the hippocampal in
vitro slice preparation." Brain Res 85(3): 423-436.
Smaragdos, G., S. Isaza, M. F. v. Eijk, I. Sourdis and C.
Strydis89-98 (2014). "FPGA-based biophysically-
meaningful modeling of olivocerebellar neurons".
ACM/SIGDA international symposium on FPGAs.
Monterey, California, USA, ACM: 89-98.
Traub, R. D. (1982). "Simulation of intrinsic bursting in
CA3 hippocampal neurons." Neuroscience 7(5): 1233-
1242.
Traub, R. D., J. G. Jefferys, R. Miles, M. A. Whittington
and K. Toth (1994). "A branching dendritic model of a
rodent CA3 pyramidal neurone." J Physiol 481 ( Pt 1):
79-95.
Traub, R. D., R. K. Wong, R. Miles and H. Michelson
(1991). "A model of a CA3 hippocampal pyramidal
neuron incorporating voltage-clamp data on intrinsic
conductances." J Neurophysiol 66(2): 635-650.
Wang, J., J. M. Geng and X. Y. Fei (2005). "Two-
parameters Hopf bifurcation in the Hodgkin-Huxley
model." Chaos Solitons & Fractals 23(3): 973-980.
Wang, L., S. Liu, J. Zhang and Y. Zeng (2012). "Burst
firing transitions in two-compartment pyramidal
neuron induced by the perturbation of membrane
capacitance." Neurol Sci 33(3): 595-604.
Zhang, Y., J. Nunez and J. McGeehan (2010).
"Biophysically Accurate Floating Point
Neuroprocessors." University of Bristol.
NeuronDynamicsofTwo-compartmentTraubModelforHardware-basedEmulation
93
