Integrating Computers, Science, and Mathematics

A Course for Future Mathematics Teachers

Alfinio Flores

Department of Mathematical Sciences, University of Delaware, Newark, DE, U.S.A.

Keywords: Mathematics Teaching, Integration of Technology, Teacher Preparation, Geogebra, Python, Modeling,

Robotics.

Abstract: A course for prospective secondary mathematics teachers was developed at the University of Delaware,

based on professional recommendations to integrate science, technology, engineering, and mathematics in

the preparation of teachers of mathematics. Students used GeoGebra, Cabri3D, and Mathematica to model

phenomena in the physical, natural and social sciences. They used motion sensors and graphing calculators

to study motion. They wrote Python programs to simulate random phenomena. They built a robot and

controlled it with a computer program, and made explicit the mathematical and scientific concepts involved

in the functioning of the robot. Several forms of formative and summative assessment were conducted

during the course. Teachers learned alternative ways of looking at mathematical concepts, and established

connections in mathematics and with other areas.

1 INTRODUCTION

Technological environments offer opportunities to

students of different skills and levels of

understanding to engage with mathematical tasks

and activities (Hollebrands, 2007). However, the

integration of technology in mathematics teaching

has been slower than anticipated due to multiple

difficulties teachers face (Hohenwarter,

Hohenwarter, & Lavicza, 2008). Having the

technology available in schools is not enough to

guarantee that teachers will know how to use it to

teach mathematics. Future and in-service teachers

need to have opportunities to develop the expertise

and know-how to be able to incorporate the use of

technology in their own teaching (Lawless &

Pellegrino, 2007).

The new course Learning mathematics with

technology offered at the University of Delaware is

geared for first-year prospective secondary

mathematics teachers. The purpose of the course is

to provide future mathematics teachers, early in their

teacher preparation program, with the knowledge

and experience of technology-based activities that

foster mathematical communication, connections,

reasoning, and reflection that help students develop

better understanding in mathematics. The course

integrates modern interactive technologies to

emphasize the learning of concepts, problem

solving, exploration in mathematics, mathematical

modeling, and connections to physics and other

sciences. The course is based on current research

and theories about how students best learn

mathematics (Boaler, 2008), incorporates

professional recommendations on the preparation of

teachers of mathematics and the type of mathematics

they need to experience and learn themselves

(Conference Board of the Mathematical Sciences,

2012; National Council of Teachers of Mathematics,

2000; Common Core State Standards, 2010,

National Research Council, 2002, 2011) and

incorporates best teaching practices. The use of

writing to learn mathematics is an important

component of the course.

2 CONTENT KNOWLEDGE FOR

MATHEMATICS TEACHERS

This course emphasizes pedagogical content

knowledge (Shulman, 1986, 1987) for mathematics

teachers. The students learn new technology,

connections of mathematics with science, and a

richer set of connections among high school

mathematical concepts. The course implements

246

Flores A..

Integrating Computers, Science, and Mathematics - A Course for Future Mathematics Teachers.

DOI: 10.5220/0004942402460251

In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 246-251

ISBN: 978-989-758-021-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

strategies and methodologies to learn and teach

mathematics with technology that could be used by

future teachers in their own classrooms. Students

actively participate in mathematical modeling of

physical, biological, and social phenomena (Gordon

& Gordon, 2010) using a variety of technology

tools, such as TI CBR 2 motion sensors and

GeoGebra (International GeoGebra Institute, 2013).

They also use hands-on materials and the computer

to further develop their own understanding of

mathematics concepts, such as conics. Throughout

the course, students use Python (Enthought, 2013)

and other programming platforms to write their own

short computer programs that involve the use of

loops (FOR or WHILE) and the use of logical

structures such as IF…ELSE.

How to work in cooperative groups was

explicitly discussed several times during the

semester. One students wrote in his end of class

reflection: “At the beginning of class, when we

talked about the concept of working together in a

group, it helped me better understand how to truly

work together and feed off of each other’s ideas.

Communication as they said, is the most important

thing about it and that helped me truly understand

the concept.”

2.1 Motion Sensors, Velocity, and

Acceleration

Students conducted several experiments with

moving objects. They captured data for position vs.

time with motion detectors and analyzed the

corresponding graphs. The very first day they used

constant-velocity vehicles (Printz, 2006). They

followed with the 7 m jump of a small stuffed toy

donkey hanging from a parachute. Students collected

distance vs. time data and described how the

different phases of the fall were reflected on the

graph (before the parachute was completely

deployed and after), and how the corresponding

parts of the graph represented constant positive

acceleration or constant velocity (initial accelerated

motion followed by falling at the terminal velocity).

One student wrote about the parachute activity on

her end of class reflection: “The effect air resistance

has on acceleration and velocity of a falling object

was a concept today’s lesson clarified for me.”

Students also captured distance vs. time data for

a bouncing basketball and analyzed the

corresponding graph (Cory, 2010), to determine

when the velocity was positive or negative, when

was the velocity increasing or decreasing, when was

it zero, etc. Especially challenging for them was to

interpret what was happening to the velocity when

the ball hit the ground.

2.2 Vanishing Points in a Rowing

Competition

Students watched a video of a rowing competition

(Allain, 2013) and then used GeoGebra and their

knowledge of perspective and vanishing points

(Figure 1 and Figure 2) to devise a way to determine

who was winning the competition. Then they wrote

a letter to a fictional television producer explaining

the advantages of their method to make it easier for

television viewers to see wheter a scull was moving

faster than another.

Figure 1: Vanishing point at t = 34.

Figure 2: Vanishing point at t = 38.

2.3 Fitting Curves to Sets of Points

Students learned ways in which GeoGebra provides

an alternative point of entry to the topic of fitting

linear and quadratic curves to two or three points.

First they played a game in pairs. One player would

position two or three points on the screen, and the

other player would use sliders corresponding to the

coefficients of linear or quadratic functions and

adjust the value of the slider to hit as many points as

possible. Students expressed that using sliders

allowed them to understand better the role of each of

the coefficients, and the advantages and

disadvantages of using different representations for

quadratic functions, such as using the coordinates (h,

k) of the vertex in the equation y = a(x - h)

+ k or

using the general equation y = ax

+ bx + c. In

another activity students used sliders to

IntegratingComputers,Science,andMathematics-ACourseforFutureMathematicsTeachers

247

experimentally fit a parabola to a set of data

representing annual growth of redwood trees vs.

rainfall.

Later, students used sliders also to fit other types

of curves such as exponential functions. Sliders were

used in addition to analytical ways to determine the

parameters of the exponential function. One activity

was to fit an exponential model to the growth of the

population in the United States during its first

century.

Figure 3: The Bubble Board.

Figure 4: Fitting a logistic curve to the bubble data.

In another activity students generated 56 soap

bubbles simultaneously with a bubble board (see

Figure 3) (Hammons, Flores, Pelesko, Biehl, 2012)

and recorded how many bubbles remained after

intervals of one minute. Then they were given the

data of the averages of nine such experiments and

were asked to use GeoGebra to fit different

mathematical models to the data (linear, quadratic,

polynomial, exponential, and logistic) and discuss

the advantages and disadvantages of each of the

models. Students found that a logistic model

y 

63.1

1 0.11e

0.37 x

(1)

fit the data pretty well in the case of the bubbles

(Figure 4).

2.4 Conics

In the United States often students’ first encounter

parabolas and other conics through equations such as

y = x

. Although textbooks mention that such curves

can be obtained by slicing a cone, students usually

do not have the opportunity to connect the different

characterizations of conics. For example, for the

ellipse, the curve can be described by the equation;

using the locus definition (the sum of the distances

to two fixed points is constant); by slicing a cone

with a plane such that the angle of cut is bigger than

the angle at the vertex of the cone; or in terms of the

ratio of the distance from a point to a line and to a

fixed point (focus-directrix). In this course students

had the opportunity to establish connections among

the different ways of characterizing conics using

hands-on models, GeoGebra, and Cabri3D. One

student expressed in her exit ticket: “Cabri3D helped

me understand conic sections better. For the

parabola, it helped me see that the distance to the

directrix and focus is equal.”

2.5 Python Programs to Simulate

Random Phenomena

The instructor conducted several short sessions

where a situation was presented, and then the class

as a whole, using plain English, described the steps

that needed to be included in a computer program to

simulate the situation. For example, one die is

tossed 1000 times. The program should keep track of

how many Heads and Tails have occurred. After

each toss the program determines who is in the lead

and keeps track how many times each player has

been in the lead. At the end the total number of

outcome for heads and tails are displayed, and also

how many times each player was in the lead, and

how many times they were tied. The instructor then

shared a program that would simulate the tossing of

the die and keeping track of the outcomes in the

desired way.

Students also did some thought experiments

about situations involving random events and then

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

248

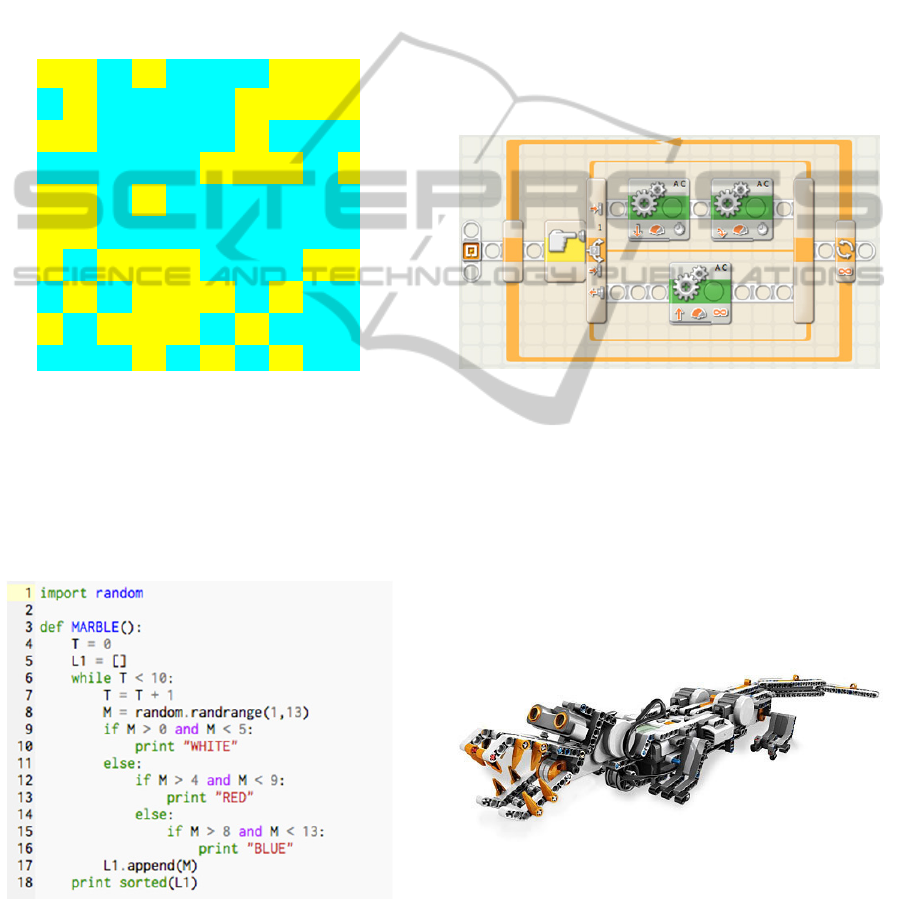
compared their results with those generated by a

computer. For instance, students were asked to

conduct a thought experiment of tossing a fair coin

100 times and fill a 10 by 10 table with the

outcomes. Students thought simulations resulted in

very fragmented tables, where tails and heads

alternate frequently. Students were then given tables

generated with Mathematica (Figure 5) to compare

the distributions of the number of squares in the

largest “island of randomness” (Flores, 2006) in

their thought experiments and those generated by the

computer.

Figure 5: Islands of randomness.

As one of their projects, students were asked to work

individually or in pairs to write their own program to

simulate a situation involving randomness. Two

students wrote a program to simulate random

sampling with replacement of marbles of three

different colors (Figure 6).

Figure 6: Random sampling with replacement.

2.6 A Robot and a Feedback Loop

The final project for the course is building a robot

controlled by a program that includes a feedback

loop. The instructor demonstrated in class a bumper

car. The bumper car moves forward until it bumps

into a wall. It moves back for one second, and turns

for 1.5 seconds, and then repeats the cycle. Thus,

inside the loop we want the bumper to do either of

two things. Change direction and rotate if it bumps

against an object, else keep moving forward if not.

Programs in Lego Mindstorms are constructed by

dragging icons, rather than typing code. For

example, the switch icon will open the IF…

THEN… ELSE part of the program. If the touch

sensor is pressed, the motor will execute the two

command on the upper part (move in reverse, and

turn). Else, the motor will continue moving forward

(Figure 7).

Figure 7: A program with a feedback loop.

One team of students chose to build a Robogator

(Figure 8). Students described the structure of the

program to control the Robogator in plain English:

IF an object is detected within 60 cm of the

ultrasonic sensor

THEN the legs will move the robot forward

infinitely

ELSE the robot does not move

IF the object is within 30 cm

THEN the jaws will open and close infinitely

Figure 8: Robogator.

Students also made explicit the scientific and

mathematical concepts involved with the robot

functioning: Velocity, speed, normal force,

momentum, friction, centripetal acceleration, torque,

feedback loops in nature depending on sensors. They

HHTHTTTHH

THTTTTHHH

HHTTTTHTT

TTTTTHHHT

HHTHTTTTT

HHTTTTTTT

HTHHHTTTH

THTHHHTHT

HTHHHTHTT

TTTHTHTHT

IntegratingComputers,Science,andMathematics-ACourseforFutureMathematicsTeachers

249

unpacked each one of these concepts further, for

example,

“Torque: The Robogator is applying torque in

order to move because its legs apply a force when

rotating around an axis, which would be the leg joint

to the motor. All of these legs are using the same

amount of torque to move at a constant speed.”

3 COURSE ASSESSMENT

Several forms of assessment were used throughout

the course, both formative and summative, ranging

from short answers in “exit tickets”, informal verbal

interviews, to a pre- and post-survey about conics,

and a survey of the class as a whole. Students’

learning was assessed through a midterm exam,

written assignments, and their reports and in-class

presentations of the final projects on Python

programs and Lego robots.

For the most part, students found the use of

technology for modeling exciting and illuminating.

After the first session a student wrote on her

reflection:

“It was surprising to begin experiments on the

first day of class; it set a captivating tone for the rest

of the semester. I was intrigued by the different

approaches each pair of students took. I look

forward to this class in order to improve my analysis

skills. Hands-on activities are an extremely helpful

tool in learning, and I am ready to have this class for

my future teaching career.”

At the end of the course, students were given a

card where they wrote on one side what to keep in

the course, and on the other what needed to be

changed or deleted. Seven out the ten participants

explicitly recommended to keep the use of

GeoGebra.

Students participated actively in cooperative

groups as they tackled complex tasks. Many had not

worked in groups before in mathematics, and found

the experience of learning from each other valuable.

One student stated that the group work and

collaboration with others “was good for learning

how others think and helped me think about math.”

Students found the course directly relevant for

their future as secondary mathematics teachers. In

addition, three peer tutors, more advanced

mathematics education students, who participated in

the course, also found this experience much more

relevant than the required computer science course

they took. Two of the peer tutors conducted an

independent study related to the course. H. Kretz

gave a survey about conics at the beginning of the

course and then again after the topic had been

covered. She found that in the beginning students

described conics using only formulas and equations,

with no mention of actually cutting a cone, or other

geometric properties. For example, one of the

students said “Each conic section is dependent on

the equation.” When asked how they would teach

the topic of conics, most students described also

approaches based on symbols, and only one student

mentioned the use of computers as a tool for

teaching conics. One student wrote “I would draw a

conic on the white board and I would show a

parabola on a calculator with y = x

and the textbook

to try looking at different equations for conics”. At

the end of the course, their descriptions of the conics

were more elaborated and they incorporated

additional geometric elements and more

connections. Likewise, at the end, the vast majority

of the students mentioned the use of computers for

teaching conics. A. Restrepo focused on students’

attitudes and dispositions towards the group work,

use of computers, and hands-on activities. After the

midterm she found that 90% of the students thought

that the hands-on activities helped them understand

and recall better.

4 CONCLUSIONS

Our course was quite successful in introducing

prospective teachers to alternative ways of looking

at mathematical concepts, emphasize connections

within mathematics, and with other areas. Van

Voorst (1999) found in a course for in-service

teachers that the use of interactive technology helped

mathematics teachers see mathematics “less

passively, as a set of procedures, and more actively

as reasoning, exploring, solving problems,

generating new information, and asking new

questions” (p. 2). We found similar changes with the

future teachers. Furthermore, our course illustrates a

point emphasized in professional recommendations

on the preparation of prospective teachers, that

teachers should have the opportunity to experience

content courses taught in the same way they are

expected to teach in High School, courses that

provide multiple points of entry to mathematical

concepts through the use of computers, hands-on

materials, and other tools. Students had also the

opportunity to experience the advantages of working

in cooperative groups and start developing their

skills for making the group work more productive.

The course will be taught again in the next

academic cycle.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

250

ACKNOWLEDGEMENTS

This course was developed as part of the grant

Integrated Science and Mathematics Education: A

Model Course for Pre-Service Teachers (S.

Bernhardt, PI, A. Flores Co-PI, H. Shipman Co-PI)

funded by the National Science Foundation. All

opinions are of the author and do not necessarily

represent the position of the funding agency.

REFERENCES

Allain, R. (2013). Physics of rowing. Retrieved December

28, 2013, from http://www.wired.com/wiredscience/

2013/04/some-rowing-physics/

Boaler, J. (2008). Promoting ‘relational equity’ and high

mathematics achievement through an innovative

mixed ability approach. British Educational Research

Journal, 34(2), 167-194.

Common Core State Standards Initiative (2010). Common

Core State Standards for Mathematics. Retrieved

December 27, 2013, from http://www.

corestandards.org/

Conference Board of the Mathematical Sciences (2012).

The mathematical education of teachers II.

Providence, RI: American Mathematical Society.

Cory, B. L. (2010). Bouncing balls and graphing

derivatives. Mathematics Teacher, 104(3), 206-213.

Enthought (2013). Canopy Python. Retrieved December

28, 2013, from https://www.enthought.com/

downloads/

Flores, A. (2006). Using graphing calculators to redress

beliefs in the law of small numbers. In G. Burrill

(Ed.), Thinking and reasoning with data and chance

(pp. 291-304). Reston, VA: National Council of

Teachers of Mathematics.

Gordon, S. P. and Gordon, F. S. (2010). Functions, Data,

and Models: An applied approach to college algebra.

Washington, DC: Mathematical Association of

America.

Hammons, A. N., Flores, A., Pelesko, J. A., and Biehl, L.

C. (2012). The “Bubble Board” and curve fitting. Ohio

Journal of School Mathematics, No. 66, 9-16.

Hohenwarter, J., Hohenwarter, M., and Lavicza, Z. (2008).

Introducing dynamic mathematics software to

secondary school teachers: The case of GeoGebra.

Journal of Computers in Mathematics and Science

Teaching, 28(2), 135-146.

Hollebrands, K. F. (2007). The role of a dynamic software

program for geometry in the strategies high school

mathematics students employ. Journal for Research in

Mathematics Education, 38(2), 164-192.

International GeoGebra Institute (2013). GeoGebra.

Available from http://www.geogebra.org/cms/

download.

Kretz, H. (2013). Teaching mathematics with technology.

Unpublished independent study report. Newark, DE:

University of Delaware.

Lawless, K. A. & Pellegrino, J. W. (2007). Professional

development in integrating technology into teaching

and learning: Knowns, unknowns and ways to pursue

better questions and answers. Review of Educational

Research, 77(4), 575-614.

National Council of Teachers of Mathematics. (2000).

Principles and standards for school mathematics.

Reston, VA: National Council of Teachers of

Mathematics.

National Research Council (2002). Learning and

understanding: Improving advanced study of

mathematics and science in U.S. high schools.

Washington, DC: National Academy Press.

National Research Council (2011). Successful K-12 STEM

education: Identifying effective approaches in science,

technology, engineering, and mathematics.

Washington, DC: National Academies Press.

Printz, J. (2006). The buggy lab: Comparing displacement

and time to derive constant velocity. School Science

and Mathematics, 106(5), 261-266.

Restrepo, A. (2013). Research 2013. Unpublished

independent study report. Newark, DE: University of

Delaware.

Shulman, L. S. (1986). Those who understand: Knowledge

growth in teaching. Educational Researcher, 15(2), 4-

14.

Shulman, L. S. (1987). Knowledge and teaching:

Foundations of the new reform. Harvard Educational

Review, 57(1), 1-22.

Van Voorst, C. (1999). Technology in mathematics

teacher education. ICTE Educational Technology

Resource Library. Retrieved February 4, 2014 from

http://www.icte.org/t99_library/t99_54.pdf.

IntegratingComputers,Science,andMathematics-ACourseforFutureMathematicsTeachers

251